轴向低频振动辅助皮质骨钻削的钻削力和温升

白小帆 侯书军 李 慨 曲云霞

河北工业大学机械工程学院，天津，300130

0 引言

骨组织是一种复杂的各向异性材料[1]。人体中的骨主要分为两种：一种是支撑躯体和承受力量的皮质骨，另一种是质地疏松的松质骨。随着治疗效果更好的骨折内固定技术逐渐普及和髋、膝关节置换技术日趋成熟，骨钻孔成为骨折治疗、假体植入等手术的必要操作之一。医生在致密坚固的皮质骨上进行钻削作业，如果施加的钻削力过大，不仅会直接导致钻削区域的骨组织产生机械损伤，还会增大钻削过程中的温升[2]。因为骨细胞的活性对温度极其敏感，当钻削区域的最高温度超过47 ℃且持续时间超过1 min时，骨细胞会发生不可逆转的热损伤甚至热坏死[3]。骨组织受到机械损伤和热损伤会导致骨强度降低、假体失稳，延长康复周期，甚至导致手术失败等严重后果[4]。因此一个成功的医疗骨钻削操作必须尽量减小钻削过程中的钻削力并减小温升。

为了更加深入地研究LFVAD方式在骨钻削过程中对钻削力和温升的影响，以及钻削参数变化对LFVAD方式的影响，本文首先进行了钻削力和温升对比实验；然后使用统计学方法识别了影响钻削力和温升的控制参数，并针对钻削力和温升进行了双目标优化；基于切削能理论和动态切削参数，使用MATLAB软件建立了钻头切削刃部分的钻削力和产热模型，并对比了相同钻削参数下CD和LFVAD方式的钻削力和产热情况。

1 振动钻削特性和模型的建立

钻头复杂的几何结构和高速运动状态使得精确表述其整体在钻削过程中的工作状态非常困难。因此采用化整为零的办法定量研究钻头切削刃部分在钻削过程中的钻削力和产热，如图1a和图1b所示，本文讨论的钻削力含进给力和扭矩。首先将切削刃整体划分为一系列独立执行斜角切削的切削单元，这些微分切削单元在钻削过程中独立进行斜角切削(图1c)；然后通过垂直于切削刃的法平面进一步简化为正交切削模型(图1d)；最后通过转换矩阵和刀具在正交切削模型中受到的垂直于前刀面的法向力Fn和平行于前刀面的摩擦力Ff求得在斜角切削模型中3个相互垂直的力，即进给力FT、切削力Fc和侧向力FL；最终通过转换矩阵计算出每个微分切削单元的进给力和扭矩。在正交切削模型中的切削热源主要由剪切变形作用生成的剪切变形热、前刀面与切屑摩擦所产生的摩擦热和后刀面与新加工表面摩擦所产生的摩擦热组成[9]。

(a)钻头侧视图

(b)微分切削单元

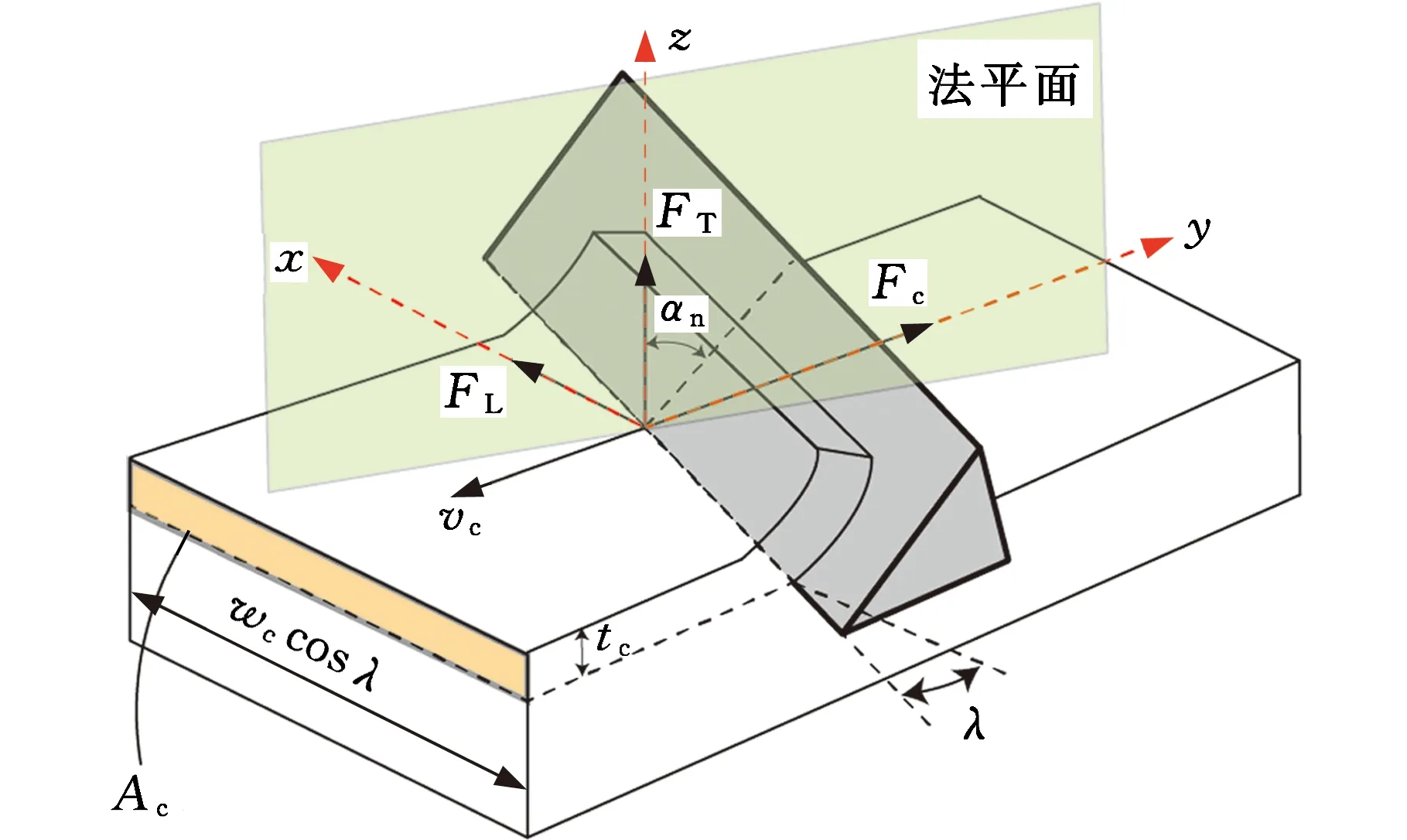
(c)斜角切削模型中的切削力

(d)正交切削模型中的切削力和热源图1 钻削过程的逐级分解模型Fig.1 Decomposition model of drilling process

在LFVAD方式下，钻头除了执行恒速进给之外还叠加了简谐运动，其运动方程变为

z(t)=vft+Asin (2πft+ψ)

(1)

(2)

式中，vf为钻头的恒定进给速度;f、A和ψ分别为叠加的轴向振动的频率、振幅和初始相位。

叠加的简谐运动使得切削刃沿其类似于正弦曲线轨迹运动，从而使切削参数发生周期性变化。切削单元的切削速度变为

(3)

vx(i)=2πr(i)ns/60i=1，2，…,n

式中，ns为主轴转速,r/min;r(i)为微分切削单元到轴心的径向距离;i为n个微分切削单元的序号。

往复的轴向运动还产生动态变化的附加前角αoff：

(4)

使得在切削进行时的实际前角变为

αreal(i)=αn(i)+αoff(i)

(5)

其中,刀具几何前角αn可按照下式[10]计算：

(6)

式中，bw为半横刃厚度;γ为螺旋角;ρ为半顶角。

由于不规则的已加工表面和类似正弦曲线的切削轨迹，LFVAD方式下切削厚度为依赖钻削参数的时变函数。设从任意时刻t0开始，钻头旋转一周产生的新加工表面S可以表示为两个切削刃轨迹S1和S2的最大值，即

S1(t)=vf(t0+t)+Asin[2πf(t0+t)]

(7)

S2(t)=vf(t0+t+Δt)+Asin[2πf(t0+t+Δt)]

(8)

S(t)=max(S1(t),S2(t))

(9)

t∈[0,60/ns] Δt=30/ns

其中，Δt为两个切削刃由于存在π的相位差而导致的时间差。切削刃在下一个旋转周期的切削厚度H可以由其运动轨迹S3和已加工表面S之间的差值进行计算：

S3(t)=vf(t1+t)+Asin[2πf(t1+t)]

(10)

(11)

其中，t1=t0+60/ns。当S3(t)-S(t)<0时可以认为钻头与骨之间脱离接触。

依据切削能理论和LFVAD的动态切削特性，可以建立LFVAD方式钻削刃部分的钻削力和产热速率模型。文献[11-12]表明骨质材料的法向切削能kn和水平切削能kf可以使用切削厚度tc、切削速度vc和前角αn的幂函数表述，其公式为

lnkn=a0+a1lntc+a2lnvc+a3ln(1-sinαn)

(12)

lnkf=b0+b1lntc+b2lnvc+b3ln(1-sinαn)

(13)

每个微分切削单元在正交切削模型中对应的力Fn和摩擦力Ff分别为

Fn(i)=kn(i)Ac(i)

(14)

Ff(i)=kf(i)Ac(i)

(15)

Ac(i)=tcwccos(λ(i))

其中，Ac(i)为切削面积;wc为切削单元的宽度;λ(i)为微分切削单元的刃倾角。

再使用转化矩阵将正交切削模型中的力转化为斜角切削模型中的进给力FT、切削力Fc和侧向力FL,可以依据下式计算:

[FTFcFL]T=

(16)

式中，ηc为流屑角，其值与刃倾角相等。

进一步推导每个微分切削单元的进给力和扭矩为

(17)

钻头切削刃部分的进给力和扭矩为各部分之和:

(18)

(19)

对于锋利的切削刀具，其后刀面与新产生的骨组织之间产生的摩擦热可以忽略不计，因此切削刃部分的产热主要包括剪切变形热Qs和刀具前刀面和骨屑之间因相对运动产生的摩擦热Qf。剪切变形热Qs生成速率可以按照下式计算:

(20)

(21)

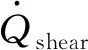
在切削过程中皮质骨的剪切屈服应力[13]：

(22)

(23)

对于皮质骨材料，C=6[13]。φn为切削单元法向平面内的剪切角，基于Ernst和Merchant理论和最小能量原理，剪切角φn为

(24)

β=tanμ

其中，β为摩擦角。设定切削刀-骨之间的摩擦因数μ=0.751[9]。剪切面面积As和剪切速度vs可以按照下式计算:

(25)

(26)

式中，φi为剪切流角度，表示在剪切平面内的剪切角度。

(27)

其中，FR(i)为各个切削单元在正交切削模型中的切削合力；vchip为切屑速度：

(28)

则钻头切削刃部分的产热速率为

(29)

2 实验材料与方法

由于牛骨的性质与人骨相似[14]，如表1所示，本实验使用新鲜牛股骨骨干作为钻削对象。在将牛骨附着的软组织和骨髓完全清除后，挑选厚度约为8 mm的皮质层切成长条状试样。在钻削之前，骨试样浸泡在生理盐水中以防止脱水和保持试样具有相同的初始温度。

表1 牛骨与人骨的相关参数[15]

实验设备组成如图2所示。多功能钻孔设备由实验室自行设计和组装，它主要由双电机自同步低频激振模块(激振频率为50 Hz，激振力为150 N)、主轴伺服电机和PLC控制系统等组成。使用六轴测力仪(Kistler 9257B，瑞士)实时记录切削过程中的进给力和扭矩，其探头使用螺栓固定在骨试样夹钳和试验台基座之间。红外测温摄像机(FLIR T1040，美国)放置在骨试样侧后方约1 m远处以测量骨组织的最高温度[16]。实验采用直径3 mm高速钢标准麻花钻头，顶角为118°，螺旋角为30°。

实验中采用的钻削参数如表2所示。在实验设备安装调试完毕后，使用激光测振仪(Polytec OFV-505/5000，德国)测定在50 Hz频率下运行时钻尖部位的轴向振幅为0.05 mm。在实验前通过接触式热电偶对红外摄像机进行标定，皮质骨的红外反射系数设定为0.96。为了消除误差，实验采用随机钻削参数，在每个钻削参数下重复钻削3次，共完成150次钻削。钻削过程中未使用润滑和冷却措施。

(a)钻骨实验设备和测试仪器

(b)钻骨实验现场图2 实验平台和钻骨现场Fig.2 Experimental platform and bone drilling site

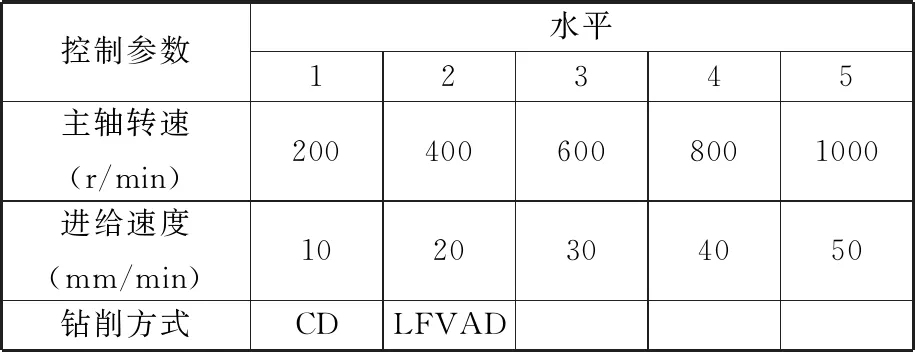
表2 控制参数及其水平设定

3 实验结果

3.1 钻削过程中的钻削力和温升

本次实验中CD和LFVAD方式的钻削力在主轴转速为200 r/min和进给速度为50 mm/min时相差最大。两种钻削方式下，一个完整钻削过程中的进给力如图3a所示。在钻削过程的稳定阶段，LFVAD的进给力峰值接近200 N，其均值接近100 N，与CD约为250 N的进给力相比减小了约60%。图3b显示了LFVAD方式在5～5.04 s期间(两个振动周期)的进给力采样值。

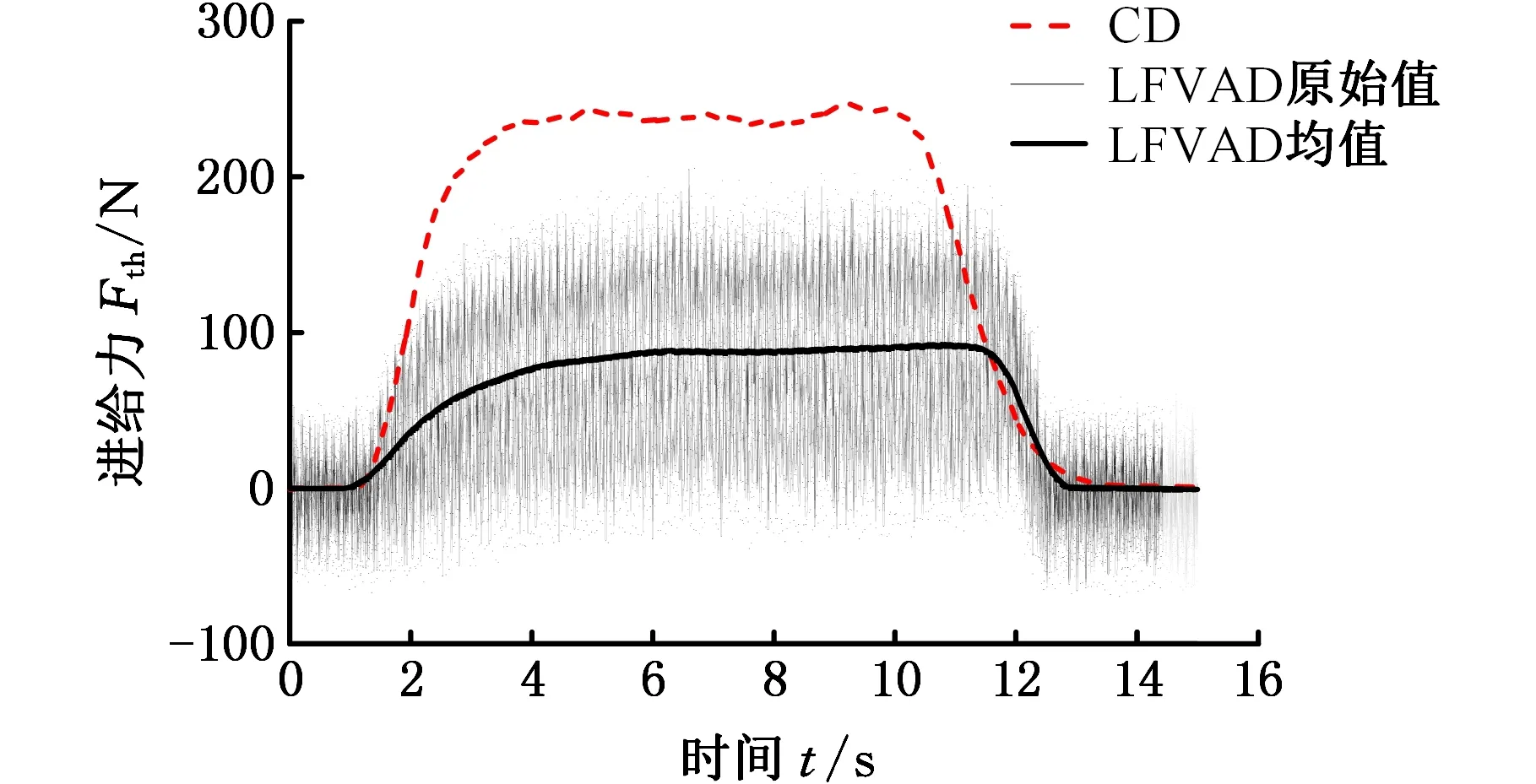
(a)完整钻削过程的进给力

(b)振动周期中的进给力图3 进给力对比Fig.3 Comparison of feed forces

对于轴向振动钻削过程中的钻削力，隈部淳一郎[17]认为由于附加在钻头上的轴向振动使工件在被切削时受到压缩力和拉伸力的交替作用，使钻削力产生周期分量，从而使均值有效降低。因此LFVAD方式的进给力Fth由平均力F1和由轴向振动引发的周期力F2组成：

Fth=F1+F2sin(2πft)

(30)

由此可以看出图3b中LFVAD的进给力Fth是由约80 N的平均力F1和峰值约75 N的周期力F2组成。

本次实验中两种钻削方式下最低温升值均发生在主轴转速为200 r/min和进给速度为10 mm/min时。在此钻削参数下的红外测温图片如图4所示，骨组织的最高温度分别为39.8 ℃和37.5 ℃(环境温度约为24 ℃),可见LFVAD的温升均值13.5 ℃相对于CD的15.8 ℃有小幅度降低。

图4 红外测温图像对比Fig.4 Infrared images of temperature measurement

3.2 钻削参数对钻削力和温升的影响

将实验结果依据不同的主轴转速ns和进给速度vf设定为5组(ns=200,400,600,800,1000 r/min和vf=10,20,30,40,50 mm/min)。各组中进给力和扭矩如图5所示。可以看出，两种钻削方式下进给力和扭矩的变化与钻削参数的变化有相似的趋势：进给力和扭矩均随进给速度的增大而近似线性增大，但随着主轴转速的增大而减小。

(a)钻削参数对进给力的影响

(b)钻削参数对扭矩的影响图5 钻削参数对进给力和扭矩的影响Fig.5 The effect of drilling parameters on the drilling force

对于温升方面，两种钻削方式下的温升随钻削参数变化的趋势如图6所示。可以看出：两种钻削方式的温升均随主轴转速的增大而线性增大；随进给速度的增大产生先升后降的趋势，其峰值发生在进给速度为40 mm/min时。钻削参数变化对两种钻削方式温升的差值没有明显影响，温升差值在各个采样点上的差值在3～5 ℃之间。

图6 切削参数对温升的影响Fig.6 The effect of drilling parameters on temperature rise

3.3 方差分析和双目标优化

对影响骨钻削过程中钻削力和温升的影响因素进行方差分析，结果显示主轴转速、进给速度和钻削方式的P值均小于0.01，因此它们对钻削力和温升都有显著影响。使用Sobol灵敏度分析确定了主轴转速对钻削力和温升具有最大影响(如图7所示)，且主轴速度的变化对两者的影响趋势相反(如图8所示)。由于手术过程中要求同时减小钻削力和温升，本文通过设计辅助函数将多个目标值归一化并进行比较:首先将各个钻削参数组合的进给力Fth和温升θ依据进给力最大值Fthmax和温升最大值θmax归一化到0～1的范围内，并设定辅助函数εθ和εF为

(31)

(32)

面积和SA可以依据下式进行计算：

(33)

其中，a和b为权重系数。由于钻削力和温升控制同等重要，因此设a=b=1。经计算，在主轴转速为400 r/min和进给速度为10 mm/min时的面积和SA达到最小，即达到钻削力和温升最优值。

(a)进给力 (b)扭矩

(c)温升图7 控制因素敏感度分析Fig.7 The contribution of control factors

(a)对钻削力的影响

(b)对温升的影响图8 控制因素的主效应图Fig.8 The main effect of control factors

4 讨论

我们认为由LFVAD较大的轴向振幅所产生的切削刀-骨之间的周期性分离运动和动态切削参数是LFVAD方式使钻削力和温升降低的主要原因。依据式(1)～式(11)分别绘出主轴转速为600 r/min和进给速度为30 mm/min时LFVAD方式下切削刃中部切削单元的切削过程和相应的动态切削参数变化曲线，如图9所示。

由图9a可以看出由于LFVAD的轴向低频振动使得切削刃与骨组织产生周期性的分离运动，使一个完整的振动切削周期分为切削阶段(如图9a切削轨迹ABC段)和分离阶段(如图9a切削轨迹中CD段)。这种独特的运动方式使得原本在CD方式中连续的切削作业变为间断性切削作业。在ABC切削阶段又可以依据切削刃的运动方向分为AB压下阶段和BC提升阶段。由图9b可以看出在AB压下阶段中切削刃的切削速度和前角均大于同时间段CD方式的值，使得切削刃加速侵入骨组织，由此聚集了剪切能量，减小了切屑的变形量并且使切削过程更加容易进行[18]，减小了切削过程中所需的钻削力，同时也减少了产热。在BC提升阶段中虽然切削前角小于CD方式的值，但是在此阶段钻头向进给反方向运动，减小的前角有利于增大反向切削力。

(a)LFVAD切削轨迹和切削区域

(b)动态切削参数图9 LFVAD方式动态切削过程示意图Fig.9 The dynamic cutting process in LFVAD method

在CD分离阶段由于钻头与骨组织脱离接触，在此阶段内钻头未遇到阻力，既不产生钻削力又不产生热量。这使得LFVAD方式的钻削力和温升的均值大幅降低。这种独特的周期性分离运动降低了切削刃-骨之间的平均摩擦因数[19]，从而降低了钻削力和摩擦热[20]。WANG等[5]认为LFVAD方式减少了骨组织中微裂纹的产生，从而减少了切削能量消耗。文献[6]则通过有限元仿真推断钻头周期分离运动产生的空气泵动效应是温升降低的主要原因。

根据表3计算出主轴转速为600 r/min和进给速度为30 mm/min时,两种钻削方式下钻头旋转一周内微分切削单元的切削能和正交切削模型中的切削力(法向力和摩擦力)，以及切削刃整体的进给力和扭矩，如图10所示。由于CD方式的切削参数恒定不变，其切削单元中的进给力和扭矩均是稳定值。LFVAD方式下切削时，切削能由于切削参数的变化而产生波动，相对应的切削力也发生变化；当切削刃与骨组织分离时，切削能和切削力都为零。因此虽然LFVAD方式的切削能和切削力的峰值大于CD方式的值，但其均值都小于CD方式的值。

表3 指定切削能系数[21]

(a)垂直进给力切削能 (b)水平进给力切削能 (c)法向力

(d)摩擦力 (e)切削刃进给力 (f)切削刃扭矩图10 不同钻削方式的切削能、切削力、切削刃进给力和扭矩Fig.10 Specific cutting energies, cutting forces， feed forces and torques on the cutting edgs under differentdrilling methods

与钻削力的情况相似，CD方式下微分切削单元的产热速率是恒定值，如图11a所示；而LFVAD方式的产热速率随着轴向运动的变化而周期性变化。虽然LFVAD方式的峰值大于CD方式的值，但是其一个周期的平均值小于CD方式的值。由于在切削刃外侧的切削单元具有较大的切削速度，在单位时间内切削做功更多，因此产生更多热量。如图11b和图11c所示，在两种钻削方式下，微分切削单元的产热速率与其钻头至轴心的距离成近似线性关系。

(a)微分切削单元产热速率对比

(b)CD方式切削刃产热分布

(c)LFVAD方式切削刃产热分布图11 产热速率对比和分布Fig.11 Comparison and distribution of heat generation rate

关于钻削参数对钻削力和温升的影响，我们认为当主轴转速恒定时，较高的进给速度直接导致材料去除率(material removal rate，MRR)提高，且使切削厚度增大，因此进给力和扭矩随其增长。此外随着进给速度的增大，切削界面处的压力增大。在切削刃和骨之间摩擦因数不变的情况下，切削界面处的压力越大，两者之间的摩擦力越大，这就产生了额外所需的钻削力和摩擦热。当进给速度恒定时，主轴转速越高，每转的切削厚度越小，切削所需的力越小。同时，PLASKOS等[22]证实了切削力与切削速度之间的相关性。由于骨的力学性能取决于应变速率，在高速切削时其所需的切削能小于低速切削时所需的能量。因此，随着主轴转速的增大，钻削力逐渐减小。ALAM等[20，23]认为在较高的切削速度下，刀具和试样之间的平均摩擦因数降低是切削力减小的原因。在产热方面，主轴转速增大的同时切削速度也近似线性增大，由式(28)和式(30)可以说明切削单元的切削热和摩擦热均与切削速度正相关，因此当主轴转速增大时温升逐渐增大。

使用模型计算CD和LFVAD方式下钻削力和温升随钻削参数变化的情况，如图12所示。可以看出，在CD方式下钻削参数变化对钻削力和温升的影响与实验结果一致；在LFVAD方式下虽然整体趋势与实验数据一致，但是个别采样点的计算结果与实验趋势不符。这表明骨组织在动态切削过程中的力学响应还需进一步探索。

5 结论

(1)与CD方式相比，在相同的钻削参数下LFVAD方式在显著降低钻削力的同时也可以减小温升。LFVAD方式下较大的轴向振幅导致的间歇性切削过程和周期性变化的动态参数是钻削力和温升减小的主要原因。

(2)使用切削能和动态切削参数相结合的方法可以较好地对CD和LFVAD方式下切削刃部分产生的钻削力和产热速率进行估算和比较。

(3)CD和LFVAD方式下钻削力和温升随钻削参数的变化具有相同趋势：钻削力随进给速度的增大而线性增大，而随主轴转速的增大而减小；温升均随主轴转速的增大而线性增大，随进给速度呈现先增大后减小的趋势，在实验设定参数范围内温升峰值出现在进给速度为40 mm/min时。

(4)使用统计分析方法可知钻削方式、主轴转速和进给速度均对钻削力和温升具有显著作用，其中主轴转速是对进给力和温升影响最大的因素。实验条件下皮质骨钻削过程的钻削力和温升双目标最优的钻削参数组合为采用LFVAD方式并将主轴转速和进给速度分别设为400 r/min和10 mm/min。

(a)进给速度对进给力的影响 (b)主轴转速对进给力的影响(c)进给速度对扭矩的影响

(d)主轴转速对扭矩的影响 (e)进给速度对输入热流量的影响(f)主轴转速对输入热流量的影响图12 钻削参数对切削刃部分钻削力和热流量的影响Fig.12 The effects of drilling parameters on drilling forces and heat flows on the cutting edges