雷击多个建筑的三维数值模拟

陈睿凌，师 正，李 杰，曲凯悦，徐佳伦

（南京信息工程大学气象灾害教育部重点实验室/气候与环境变化国际合作联合实验室/气象灾害预报预警与评估协同创新中心/中国气象局气溶胶与云降水重点开放实验室，南京 210044）

雷电是发生于大气层中一种强烈的瞬时放电现象［1］，它会对人类社会产生严重的危害。观测研究表明，相对于地面和矮建筑物，闪电更易击中高层建筑，尤其是高层建筑的顶端及角落处［2-5］。雷暴云过境时，建筑物的顶端和角落处容易产生电场畸变，相对于低矮建筑物，高建筑物对空间电场产生的畸变作用更强，上行先导更容易从此处产生。因此，当两个或多个建筑物距离较近时，高建筑物能保护低建筑物，使得低建筑物遭受雷击的概率减小或避免雷击。但实际对高建筑物的具体保护范围缺乏足够的研究，随着社会经济的快速发展，现代城市中高建筑物越来越多，建筑物的高度分布情况也更加复杂，同时，全球变暖导致闪电活动频繁［6］，因此研究多个建筑物间雷击保护效应有着广泛而深远的意义。

传统的雷击概率算法是基于电气几何模型来计算的［7］，这种算法没有考虑建筑物高度、建筑物几何尺寸的影响，也没有考虑上行先导的始发过程，简化了闪电放电过程，难以适用于高建筑物的雷击概率计算。针对电气几何法的局限性，Eriksson［8］提出了收集体积法（Collection volume method），但其有效性仍存在争议［9］。为了能较为准确地计算雷击概率，需要对雷击建筑物进行进一步的研究。闪电的实地观测研究具有很大的局限性，难以进行多次试验，且试验过程不可控，成本较高。而数值模式的方法可以进行大量多次试验，并且能对需要研究的参数进行控制和调整，成本低廉。因此，利用数值模式进行闪电相关问题的研究已经成为一种重要手段。Becerra等［10］提出了一种自适应的上行正先导发展模式。Dul’zon等［11］建立了一种下行先导随机发展模型。Mansell等［12］在前人研究的基础上，把随机介质击穿模式应用到雷暴起电放电的数值模拟中，使数值模拟得到的闪电更接近真实闪电的形态。李丹等［13］建立了一个闪电先导三维空间内自持发展的模式，模拟了上行先导的发展速度、线电荷密度、电荷量、电流强度等参数。任晓毓等［14］建立了先导三维随机模式，并通过与二维模式的对比验证了三维模式的准确性。谭涌波等［15-18］针对先导与建筑物的连接过程，模拟了二维模式下高建筑物对低建筑物的雷击保护作用，得出雷击保护临界距离与建筑物高度有关［18］。

研究采用三维先导连接模式［19］，以地面上空400 m×400 m×750 m模拟区域，对每组试验保持模式中的其他参数不变，仅调整随机性参数，从而得到不同的闪电通道形态，对不同建筑物分布条件下的闪电进行多次模拟，通过分析雷击先导的轨迹、雷击建筑物的落点位置，探究三维先导发展模式中建筑物群间的保护效应以及雷击保护概率与建筑物特征参数间的关系。

1 三维先导模式设置

构建一个400 m×400 m×750 m的三维空间模拟域，分辨率为57 m×5 m×5 m，模拟域内电场分布均匀。模拟域中设置一个高建筑物模型和一个低建筑物模型，建筑物都设置在y轴的中轴线上，讨论建筑物的高度及间距对闪电发展形态的影响，因此认为闪电在云内随机发展，直到下行先导达到近地面层，才会被地面建筑物影响（图 1）。Erikssom［8］的观测结果表明近地面的闪电无法向上发展，因此本研究在模拟域上部设置一初始先导，引入先导放电参数化方案，根据先导通道和周围环境的电位，确定先导下一步发展方向。建筑物模型与地面良好连接，保持零电位。建筑物边界、模拟域上边界、先导的电场在此边界处恒为常数，满足狄利克雷边界条件；模拟域侧边界电场在此边界处的法向向量恒为常数，满足诺依曼边界条件。先导发展过程为步进式发展，即先导通道每次只发展一个格点。通过计算可以求出空间电场中相应格点的场强。空间格点的电场强度可以通过有限差分法解出。考虑到先导对周围电场环境的影响，先导每发展一步后，需对空间电场重新进行计算。上行先导和下行先导分别发展，求得先导间的电场强度，并与设定好的阈值相比较，若超过连接阈值，则判定为先导连接，即一次地闪过程。根据研究需要，改变建筑物尺寸参数，改变随机参数，进行多次敏感性试验。设定下行先导和上行先导始发阈值为 150 kV/m，连接阈值为 500 kV/m［20］。设置初始先导位于建筑物的中央顶部，初始长度为25 m，初始电场为150 kV/m。

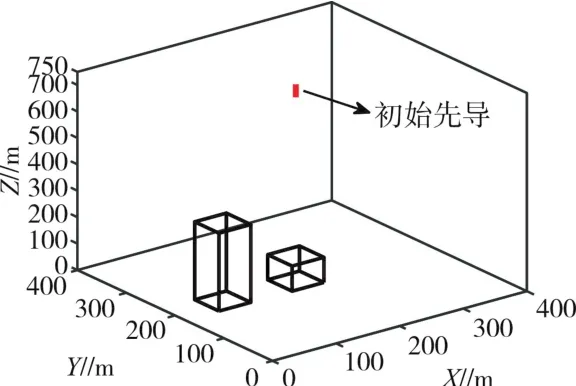
图1 三维空间模拟域

为保证模拟出的闪电符合自然观测结果，采用先导随机模式，即先导通道每次只发展一个格点，求取空间电场内当前格点和周围格点的场强，利用随机概率函数确定先导下一步发展的方向，概率函数如下：

式中，Pi为概率，Ei为闪电通道周围第i个点与该通道之间的电场强度，E0是设置的击穿阈值，α是加权指数，Ek为空间中每个可能连接发展的格点电场强度。

2 结果与分析

2.1 雷击落点统计

首先设置高建筑物高度为300 m，低建筑物高度为100 m，建筑物长宽均为50 m，建筑物间距为D（取值从15 m开始，每组间距增加10 m，直到间距为165 m），共得到16组建筑物间距不同的试验组。在仅改变随机参数的条件下，对每个试验组进行50次敏感性试验，得到不同建筑物间距条件下多组闪电空间发展形态。根据雷击点（上行连接先导始发点）的不同，将雷击落点细分为击中高建筑物拐角、击中高建筑物顶面、击中高建筑物顶边、击中高建筑物侧面、击中高建筑物侧边、击中低建筑物拐角、击中低建筑物顶面、击中低建筑物顶边、击中低建筑物侧面、击中低建筑物侧边和击中地面11种类型。图2a至图2k为以上11种雷击落点的示意图，红色为下行先导，蓝色为上行连接先导。由图2可知，闪电的发展形态和雷击落点呈现很强的随机性。同时，所采用的三维模式模拟出的闪电分叉数和复杂性远远超过二维模式模拟结果［12］，与真实地闪观测结果更为接近。

图3给出了闪电击中高建筑物、低建筑物和地面的统计数据，当两建筑物距离较近时，闪电多击中高建筑物而几乎不击中低建筑物，随着建筑物间距逐渐增大，击中低建筑物的雷电数逐渐增加，击中高建筑物的雷电数逐渐减少，当两建筑物间距超过105 m后，雷电更易击中低建筑物，此时两建筑物已经相距较远，可以视为2个独立的建筑物。由此可见，在两建筑相距较近，建筑物间距没有超过100 m时，高建筑物对低建筑物存在一定的保护作用，在建筑物间距为15～45 m时，高建筑物对低建筑物的保护作用尤为明显。

图2 不同的雷击落点

图3 雷击落点统计

为了研究高建筑物保护效应的产生原因，选取闪电分别击中高建筑物拐角和低建筑物拐角的2次模拟过程，分别计算先导发展过程中高建筑物4个拐角（A、B、C、D）和低建筑物4个拐角（E、F、G、H）处电场畸变值，图4给出了8个拐角A、B、C、D、E、F、G、H处电场畸变值随先导发展步数的变化。由图4可知，随着下行先导的步进式发展，高、低建筑物的拐角处均产生电场畸变，但不同拐角上产生的电场畸变程度差异很大，从图4b和图4d可以看出，在初始条件下高建筑物拐角的电场畸变值大于低建筑物，高建筑物两侧拐角电场畸变值相等，低建筑物内侧拐角电场畸变值明显小于外侧拐角。下行先导发展初期，高建筑物和低建筑物拐角处的电场畸变值增加较为平缓，高建筑物电场拐角处畸变值增长速率略高于低建筑物，当下行先导临近时，电场畸变值呈指数增长，距离下行先导越近的拐角电场畸变值增长速度越快。如图4b所示，下行先导的发展过程中，先导通道顶端距离高建筑物较近，C拐角电场畸变值急剧增大，达到上行先导始发阈值150 kV/m，在高建筑物拐角C处产生上行连接先导与下行先导连接，闪电击中高建筑物C拐角。而图4d中，在发展前期先导通道顶端距离高建筑物较近时，高建筑物上拐角的电场畸变值虽然快速增大，但并未达到始发阈值，因此没有产生上行先导。先导继续向下发展，先导通道顶端逐渐远离高建筑物拐角，接近低建筑物拐角。此时，高建筑物拐角的电场畸变值增长速率减小，而低建筑物拐角的电场畸变值开始快速增长，F点电场畸变值发生跃变，达到上行先导始发阈值150 kV/m，在低建筑物拐角F处产生上行连接先导与下行先导相连接，闪电击中低建筑物拐角F。由此可见，雷击建筑物的落点位置与建筑物各位置引发的电场畸变密切相关，高建筑物的拐角能够引发更强的电场畸变，在高建筑物拐角附近的电场梯度高于低建筑物，电场更强，因此，上行先导往往出现在高建筑物的拐角处，体现为闪电更容易击中高建筑物，低建筑物被闪电击中的可能性则随之减小。

图4 建筑物拐角处电场畸变值随先导发展步数的变化

2.2 保护效率的影响因素

为进一步探究高建筑物对低建筑物保护效率的影响因素，在模拟域内添加特定建筑模型进行以下试验：首先，设置初始先导位于低建筑物上方中心，保持2个建筑物的尺寸参数（高建筑物高度H1=250 m、宽度W1=50 m，低建筑物H2=100 m、宽度W2=50 m）不变，仅改变建筑物之间的距离D（取值从15 m开始，以步长10 m逐步增加，取值范围为15～165 m），规定每个D值为一组，对于每组试验，调整闪电的随机性参数，每组共计50个随机性参数，进行50次模拟试验。记录低建筑物被闪电击中的情况和数据，结果如图5、图6所示。由图5可知，随着距离的逐渐增大，低建筑物被雷击次数呈递增趋势。由图6可知，高建筑物对低建筑物的雷击保护概率与建筑物之间距离呈现明显的线性关系，由此可知高建筑物对低建筑物的雷击保护概率P在一定范围内与2个建筑物间的距离D呈线性相关。然后设置低建筑物高度为100 m，宽度为50 m，保持不变。设置3组高建筑物高度H（H取值分别为200、300、350 m），在保持其他参数不变的条件下，改变建筑物间距离D（取值从15 m开始，以步长10 m逐步增加，取值范围为15～165 m），可以得到64组，每个试验组通过改变随机参数进行50次敏感性试验，分别得出不同高度条件下高建筑物对低建筑物的雷击保护概率P。图7是不同高度的高建筑物与保护概率的关系曲线，由图7可以看出，建筑物高度一定的情况下，高建筑物对低建筑物的保护概率与建筑物间距呈一定的线性关系，这与前文得出的结论是一致的，而当建筑物间距一定时，高建筑物的高度越高，高建筑物对低建筑物的保护概率越大。分析其原因，在建筑物间距、建筑物宽度相同时，建筑物高度越高，周围电场产生的畸变越剧烈，下行先导越容易向此处发展，即对低建筑物的保护概率越大。

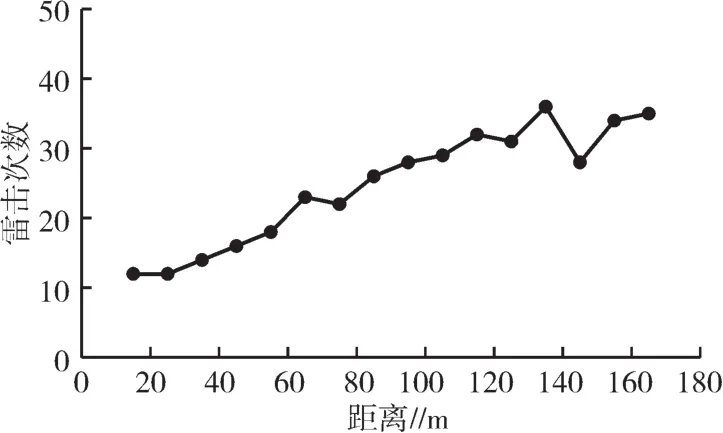
图5 低建筑物雷击次数与建筑物之间距离的关系曲线

图6 高建筑物对低建筑物雷击保护概率与建筑物之间距离的关系的拟合曲线

图7 不同高度的高建筑物与保护概率的关系曲线

上述分别研究了高建筑物对低建筑物的保护效率与两建筑物间距和高建筑物高度之间的关系，但仅考虑了单个因素对保护概率的影响，对于多因素影响下的保护概率则没有讨论。因此，对上述2个参量即高建筑物高度和两建筑物间距进行多元线性回归分析，将64组数据进行多元线性拟合，得到了雷击保护概率P与高建筑物高度H和两建筑物间距DX的关系式：

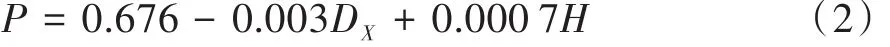
式中，P为高建筑物对低建筑物的雷击保护概率，DX=D+W，D为两建筑物间距，W为建筑物宽度，决定系数R2=0.834 5，两者具有较强的相关性。

3 小结与讨论

以近地面上空400 m×400 m×750 m的三维空间模拟域为研究区域，使用三维先导放电方案，保持方案中的其他参数不变，通过改变两建筑物的间距和高度，对同一高、低建筑物分布情况下的雷电发展与连接过程进行多次模拟，得到如下结论。

1）高建筑物对低建筑物存在一定的保护作用，在建筑物间距为15～45 m时保护作用尤其明显，当建筑物距离位于这个区间时，闪电几乎不会击中低建筑物，且保护作用存在一定的临界距离，临界距离约为100 m，在建筑物间距超过临界保护距离后，高建筑物对低建筑物的保护作用不再明显。总体来看，建筑物间间距越大，高建筑物对低建筑物的保护概率越小，二者存在明显的线性关系。进一步分析高建筑物对低建筑物保护效应的产生原因，雷击建筑物的落点位置与建筑物各位置引发的电场畸变密切相关，高建筑物的拐角处空间电场更容易产生畸变，并且空间电场在此处的场强也更强，因此上行先导往往出现在高建筑物的拐角处，体现为闪电更容易击中高建筑物，在建筑物群中，低建筑物则更不易被闪电击中，高建筑物对低建筑物有一定的保护效应。

2）为了进一步研究影响雷击保护效率的因素，在对多组不同建筑物参数条件下雷击落点的统计数据进行分析后得出，在建筑物间间距相同的条件下，高建筑物的高度越高，闪电击中高建筑物的可能性越大，其对低建筑物的保护概率就越高，但其保护效果随着建筑物间间距增大的衰减也越明显。在建筑物高度一定的条件下，两建筑物间距越大，雷电击中高建筑物的可能性越小，其保护概率越低。最后对高建筑物的高度和建筑物间距对雷击保护概率的影响进行了多元线性分析，给出了一个适合不同高度不同间距的建筑物群雷击保护概率计算公式。

简化了一系列复杂物理过程，模拟结果与参数化方案的设置有很大关系，结果的普适性仍需讨论。而保护概率仅考虑了高建筑物高度和建筑物间距的影响，实际情况中建筑物群各个建筑物的高度分布更加复杂，且建筑物数量更多，关于低建筑物高度的改变对保护概率的影响以及三个或更多建筑物遭雷击时的保护概率问题，仍需进一步的试验以及大量观测和实际工程案例验证。