基于小波变换的抑制复位噪声技术研究
2021-02-22张天瑶梁铭珊邓盼盼
潘 良,张天瑶,梁铭珊,邓盼盼
(西安现代控制技术研究所,西安 710065)
0 引言
干涉式光纤陀螺是一种基于Sagnac效应的光学传感器,因具有低功耗、小体积、高带宽、快响应速度以及高振动可靠性[1-2]等一系列优点而被广泛应用于惯性导航领域。但是受限于光学器件工艺水平,目前的光纤陀螺输出信号通常含有大量的噪声且非平稳的[3]。Y波导调制器(多功能集成光学调制器)在光纤陀螺信号调制和反馈环节中起到神经中枢的作用,所以其性能的优劣直接影响光纤陀螺的性能。Y波导调制器主要用铌酸锂晶体制成,原理是通过施加电场改变晶体折射率,从而改变波导中光波的光相位差,从而实现相位调制的功能。需要指出的是,Y波导在某些频率加载半波电压进行跳变时,调制相位有明显的阶跃,高精度陀螺的毫秒输出有一个和该调制相位阶跃信号同步出现的阶跃变化,称该阶跃变化为复位噪声。复位噪声的幅值和光纤陀螺的白噪声处于同一数量级,直接影响光纤陀螺的零偏变化。该复位噪声湮没在中低精度光纤陀螺的热噪声内,但是对于高精度光纤陀螺的影响不能忽略。为降低复位噪声对零偏的影响,本文对复位噪声的特性进行了分析,并利用小波滤波方法,选取合适的小波基和分解层数,在满足系统实时性要求的基础上,实现对复位噪声的抑制。
1 Y波导复位调制相位漂移引起的零偏误差
1.1 Y波导的调制相位漂移
当在Y波导的电极处加载外电场时,由于电极设计或者工艺上的缺陷,导致电极之间的介质(包括衬底、水汽等)中的自由电荷(如金属离子、氢离子等)会在施加电场的电极附近形成一个额外附加电场,该附加电场与原施加在Y波导上的电场方向相反[4],该现象称为Y波导调制器的相位漂移。在该情况下,加载在Y波导上的有效电场减小,使得外加电压的作用效率下降,表现为半波电压发生改变。
而当Y波导电极处加载外电压为半波电压跳变时(复位过程),调制相位也有一个阶跃变化。复位的频率直接影响感应电场的变化。
1.2 高精度陀螺信号检测模型
闭环光纤陀螺的信号流程[5]如图1所示。闭环光纤陀螺中数字解调结果对应的是转速引起的相位差Δφs和反馈相位差Δφf之间的闭环误差Δφe。解调得到的闭环误差进入积分器,积分器输出即为光纤陀螺当前时刻的转速,同时也作为新的阶梯波台阶高度生成阶梯波进行反馈。最基本的光纤陀螺闭环控制系统本质上是一个一阶控制系统,可以无静差的跟踪输入转速的变化。

图1 光纤陀螺的信号流程图
光纤陀螺的信号检测模型已经在导航级光纤陀螺的相关研究中被较完整地建立与讨论。本文主要关注的是加载在Y波导的电压在复位过程中,光纤陀螺的信号误差检测。施加在Y波导上的阶梯波调制信号如图2所示。

图2 阶梯波调制信号
图2中(a)表示光纤陀螺敏感天向时,阶梯波的累加复位波形,(b)表示阶梯波复位时刻波形。光纤陀螺闭环系统闭环到零的微分方程如公式(1)所示:
(1)
其中,Δφs表示Sagnac相位差,对应输入的转速信号;Δφf表示阶梯波产生的调制相位;φf的微分部分表示反馈相位差(Δφf)用来补偿Δφs,同时也是转速的输出量。e(φf)输出量表示波导复位时Y波导调制相位漂移参与闭环的误差项。假设复位时刻,误差项解调结果与阶梯波产生的绝对相位近似线性关系,e(φf)可表示为k(φf)。因此变化后如公式(2)所示:
(2)
公式(2)的解如公式(3)所示:
(3)
对应的输出转速为公式(4):
(4)
可以看出,由于复位相位变化,输出转速的绝对值会小于Δφs。Δφf初始值为0,φf=2π时,由公式(3)可以求得对应的时间。因此复位所需要的时间如公式(5)所示:
(5)
将公式(5)带入公式(4)中,得到复位时的输出转速为-Δφs+2kπ。从t=0到复位时刻,输出转速从-Δφ到-Δφs+2kπ变化,表现为输出转速的阶跃跳变。在这个复位周期T内,输出转速的平均值约为:
(6)
由公式(6)可知,受到干扰项的影响,输出平均转速的绝对值将小于Δφs,且复位过程调制相位变化造成的附加零偏大小和复位频率有关。将某型号高精度光纤陀螺的输出数字量以毫秒周期发送,并且通过RS422串口发送至上位机,通过MATLAB解析后的原始数据如图3所示,(a)表示天向陀螺静态原始输出波形,(c)表示南北向陀螺静态原始输出波形,(e)表示东西向陀螺静态原始输出波形,(b)、 (d)和(f)分别是(a)、(c)和(e)的某短时间片的局部波形。图3(a)的零偏输出为8.39°/h ,图3(c)的速率输出为12.28°/h,图3(e)的速率输出为0.01°/h。图(b)的复位噪声周期840 ms,图(d)的复位噪声周期560 ms,图(f)的复位噪声无明显周期性规律。复位噪声明显拉低了零偏的输出,复位噪声和信号检测模型吻合。从图3中可以看出,复位噪声受转速影响,转速越大复位噪声频率越大,转速越小复位噪声频率越小。对于高精度光纤陀螺,由复位噪声引起的零偏变化是不可接受的。

图3 光纤陀螺原毫秒数据输出波形
引起复位噪声的主要原因是,Y波导半波电压跳变过程中的调制相位变化引起的。要抑制该噪声,可以通过以下两种途径,(1)通过优化Y波导的电极设计方案,使得无论半波电压跳变的频率如何变化,Y波导的波形斜率都不会在复位时刻发生明显畸变;(2)通过软件算法,设计合理的滤波器,在保证信号完整性和不失真的基础上,滤掉复位噪声。本文主要研究小波滤波抑制复位噪声的方法。
2 小波滤波
2.1 小波在实时系统应该中概述
目前光纤陀螺主要采用均值滤波去噪。均值滤波算法简单,实时性高,适用于稳态信号的去噪。然而复位噪声是高精度光纤陀螺输出信号中的非平稳噪声,均值滤波不能滤掉。小波滤波不但可以提取出低频信息的特征,而且同时会保留高频信息的特征。本文提出的小波滤波算法的基本思想是通过施加滑动滤波数据窗的方式,总剪取实时数据的最新一段,利用区间小波去噪算法,构造出实时小波去噪算法。此算法通过选用具有正交和紧支撑性质的Daubechies小波和Mallat[6]的多尺度变换算法来提高信号处理速度;通过限制滑动数据窗的长度进一步减少了计算量,虽然去噪效果与离线小波滤波处理结果有一定差距,但是可以明显地去除复位噪声这一非平稳噪声。
2.2 最优小波基和层数确定
光纤陀螺的输出信号在不同频段上的能量分布必然和无复位噪声时不同。由于光纤陀螺的信号为非平稳信号,采用小波包分解可以获取信号的低频和高频信息。
复位噪声具有阶跃性,有一定的随机噪声成分。因此应选择适当消失矩且对称性和正则性较好的小波函数。经过反复试验,本文选用的是消失矩为4的Daubechies小波族中的db4小波,其小波函数图像如图4所示。
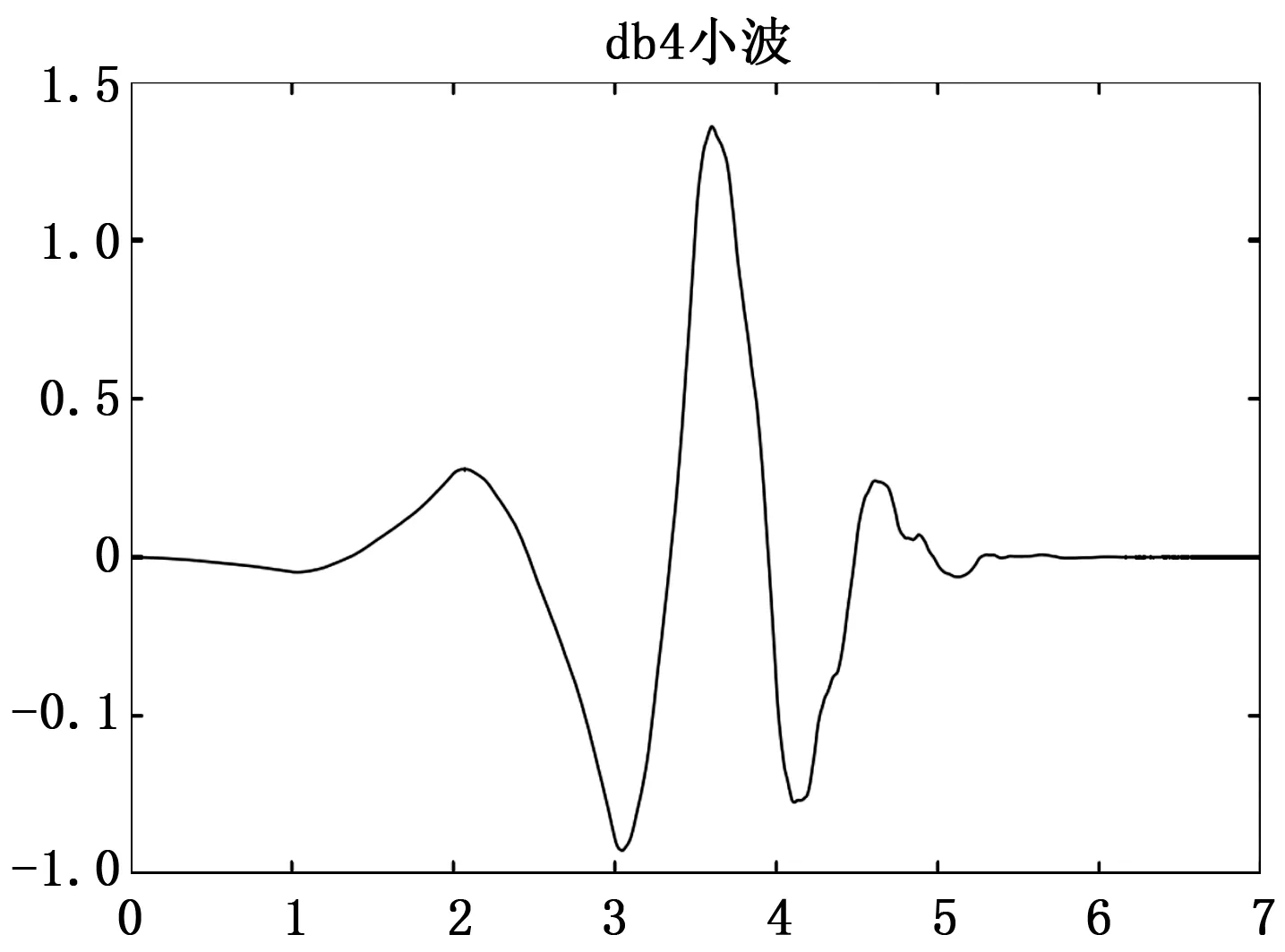
图4 db4小波
使用db4小波函数对光纤陀螺的输出信号进行分解时,需要选择合适的分解层数。选择过多的分解层数可以获取的频段信息更细腻[7],但是,计算量会显著增加而影响系统的实时性, FPGA的硬件资源有可能被小波包的分解、重构大量消耗甚至无法生成硬件电路。如果使用过少的分解层数,频段的分割就会过于粗糙,高频、低频段的信息无法区分,导致去噪效果下降。经过反复实验验证,本文使用db4小波进行3层小波分解,如图5所示。

图5 3层小波包分解
小波变换的双正交基来自于小波函数和尺度函数,而其通过scale和平移来得到的小波函数族和尺度函数族表示了不同小波函数的分辨率。
3 FPGA实现
由于系统对信号处理的实时性要求较高,而小波的分解和重构需要进行大量的并行运算,所以采用具有强大可编程能力的FPGA[8]来满足信息处理过程中的高时序要求,并结合光纤陀螺双闭环反馈算法框架,对小波滤波算法在FPGA上的可实现性进行研究。
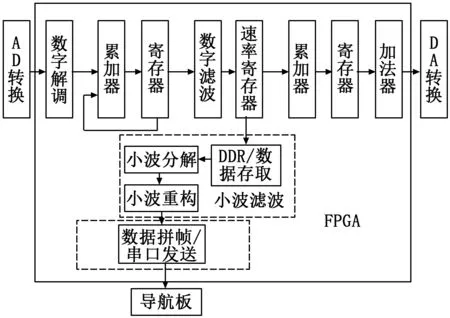
图6 FPGA总设计框图
Verilog HDL是目前应用最广泛的一种硬件描述语言[9],可用它进行各种级别的逻辑设计。小波滤波器的设计属于复杂算法的电路设计。小波变换直接计算量很大,Mallat基于多分辨率分析框架,提出小波变换的金字塔算法,极大降低了计算复杂度,并广泛的用于各种实践中。根据多分辨分析(MRA)方程[10]离散的小波变换分解算法如图7所示,其中,h0[k]是尺度函数系数,h1[k]是小波函数系数,cj[k]表示信号的粗略信息(低频段),dj[k]表示信号的精细信息(高频段)。

图7 小波三级分解框图
信号经过小波函数系数(尺度函数系数)之后还需要经过一个内插的过程,需要指出的是必须先抽取再滤波,不能先滤波后再内插。三级小波重构过程如图8所示。

图8 小波三级重构框图
按照算法流程实现小波变换,在这个过程中必须要进行多相分解,如果不采用多相结构,相当于原信号先经过了一次抽取,这极大的浪费了信号,所以对信号和滤波系数都要进行奇偶分解,分别进行滤波。设计奇偶分解的模块,实际是做一个二分频时钟,上升沿将数据写入偶数部分,下降沿将数据写入奇数部分,此过程使用三段式状态机,以确保建立时间和保持时间是信号保持时间的一半。Matlab获取滤波系数代码如下,先生成,再量化。
wn = 'db4'
%先生成,Ld:低通分解;Hd:高通分解;Lr:低通重构;Hr:高通重构
[Ld,Hd,Lr,Hr] = wfilters(wn);
%量化
qua_ld = round(Ld*2^8);
qua_Hd = round(Hd*2^8);
qua_Lr = round(Lr*2^8);
qua_Hr = round(Hr*2^8);
FPGA的模型比较复杂,完成编码后的三层小波滤波算法的RTL级分析原理如图9所示。
4 实验验证
实验过程中,采用的光纤陀螺由环长度1 400 m、直径76 mm的光纤环和波形斜度较大的Y波导组成,适配合适的陀螺程序参数,使光纤陀螺达到最佳性能。烧写初始程序后,测试该陀螺仪静态零偏。由于东西向复位噪声影响小,所以以东西向的输出作为该陀螺的固有零偏,且测得固有零偏为-0.012°/h。然后分别测试天向、南北向原始程序和小波滤波程序后的输出偏值、零偏(输出偏值除去西安实验环境角速度分量)、毫秒零偏稳定性、100秒零偏稳定性,具体测试结果如表1所示,采集后的各种情况波形如图10所示。

图9 三级小波滤波RTL原理图
从表中可以看出光纤陀螺加载均值滤波程序,南北向零偏变化大于天向零偏变化,且两个方向的零偏均明显小于固有零偏,转速对零偏的变化影响较为明显。加载小波滤波程序后,南北向零偏变化大于天向零偏变化,但是幅值明显降低,两个方向的零偏较固有零偏的变化和光纤陀螺的分变率(0.005°/h)处同一水平,所以转速对零偏的变化可以忽略不计。
图10中(a)和图(c)中能明显看到小波滤波后2 ms数据的复位噪声依然存在,但是其幅值明显小于原始程序数据,图(b)和图(d)可以看出天向的复位噪声频率为1.2 Hz,南北向的复位噪声频率为1.78 Hz,小波滤波后的基频能量明显小于原始程序能量。图(e)和图(f)是100 s平滑后的零偏曲线,由数据和波形可知,原始程序数据和小波滤波数据趋势相同,且二者的噪声水平相当。所以,小波滤波相比较均值滤波而言,光纤陀螺的零偏不再随转速的变化而改变,提高了光纤陀螺的固有零偏重复性。小波滤波后的毫秒级数据噪声带明显优于均值滤波方法。100 s滤波稳定性二者处同一水平。
5 结束语
本文详细分析了光纤陀螺复位噪声对输出零偏影响的理论,在此基础上提出了FPGA内部实现小波滤波去复位噪声的方法,最后通过实验验证,小波滤波对2 ms复位噪声具有良好的抑制效果,且噪声带明显变小,然而无法抑制长期趋势向漂移。复位噪声和Y波导的复位频率有关,因此采用小波滤波抑制复位噪声后,光纤陀螺的零偏输出不会因为转速的变化而变化。对于一些应用于短时航向对准的光纤惯导系统而言,本文提出的小波滤波抑制方法具有一定的工程意义。

表1 均值滤波和小波滤波不同方位的测试数据 (单位:°/h)
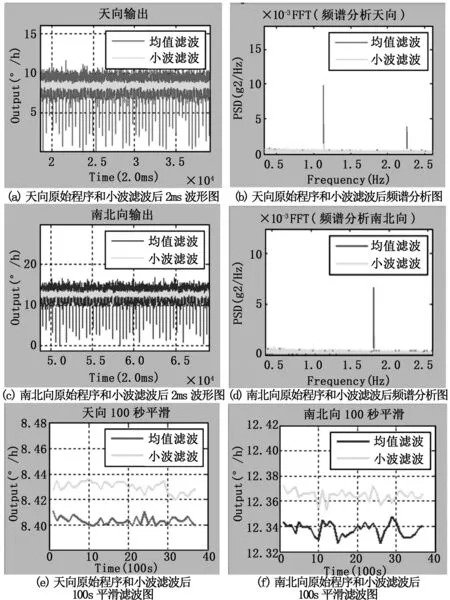
图10 各情况波形
