基于前期雨量和降雨历时的SCS-CN模型改进
2021-02-19吴艾璞王晓燕黄洁钰黄静宇李泽琪
吴艾璞,王晓燕,2,黄洁钰,黄静宇,王 俊,李泽琪
基于前期雨量和降雨历时的SCS-CN模型改进
吴艾璞1,王晓燕1,2※,黄洁钰1,黄静宇1,王 俊1,李泽琪1
(1. 首都师范大学资源环境与旅游学院,北京 100048;2. 首都师范大学首都圈水环境研究中心,北京 100048)
径流曲线法(Soil Conservation Service Curve Number,SCS-CN)对前期产流条件(Antecedent Moisture Condition,AMC)的概化,导致径流预测出现相应的突然跳跃,同时还忽略了降雨历时作为重要组成部分对地表径流的影响,影响了模型径流预测的精度。密云水库是北京市地表饮用水的重要来源,对其上游流域进行降雨径流预测有着重要的生态意义和经济意义。该研究将SCS-CN模型与前期雨量和降雨历时结合,采用API(Antecedent-Precipitation Index,前期降雨指数)模拟土壤前期水分条件,并且提出了一种考虑次降雨事件中土壤前期雨量和土壤入渗量的静态渗透方程,对SCS-CN模型进行了改进。其中,潜在最大蓄水等于前期土壤水分和土壤潜在蓄水量的和,最大静态渗透速度是流域土壤水分达到蓄满时的静态渗透速度,静态渗透系数是与土壤结构、土地利用等相关的无量纲。利用2006—2010年及2014—2020年石匣流域径流小区的200次降雨径流事件监测结果,对该研究改进的模型与原SCS-CN模型以及两种前人改进的SCS-CN模型进行了校准、验证和性能比较。结果表明,4种径流模型中,该研究改进的模型表现最好,纳什效率系数为0.77,决定系数为0.79,均方根误差为3.21 mm,相比于SCS-CN模型纳什效率系数、决定系数分别提高了319%、97.5%,均方根误差降低了107.5%。参数敏感性分析表明,潜在最大蓄水和静态渗透系数是最敏感的两个参数,最大静态渗透速度的参数敏感性一般,初损率的参数敏感性最差。该研究改进模型在密云水库上游潮白河流域降雨径流模拟中具有一定的适用性,可为其他地区产流计算提供参考依据。
径流;模型;降雨;SCS-CN模型;前期降雨指数;降雨历时
0 引 言
地表径流是水文循环的重要组成部分,是洪涝灾害、水土流失及非点源污染发生的重要驱动力。地表径流的估算已在水资源管理、防洪、水土保持、水利工程建设及流域评价等各个方面发挥着重要作用[1-4]。众多学者们通过使用下渗模型来计算径流,如Philip模型、Green-Ampt模型和Horton模型,但这些模型存在所需参数过多且难以获取的问题[5]。基于降雨对流域进行地表径流估算的降雨-径流模型是另外一种重要方法[6-7],美国农业部水文学家开发的SCS-CN径流曲线模型因其结构简单、参数获取方便等特点而被大家所接受[1,5,8]。众多实例表明,SCS-CN模型是一种方便、有效的径流模拟方法[9-11]。SCS-CN径流模型也已经被应用到许多水文和水质模型,如CREAMS模型、EPIC模型、SWAT模型、EFTC模型,以及AGNPS模型[12-14]。
初始土壤水分条件是影响地表径流的重要因素,曲线数(Curve Number,CN)是SCS-CN模型中作为反映土壤潜在蓄水量的一个参数,SCS-CN模型计算的径流深对参数CN敏感性极强[15]。现有的SCS-CN模型中,CN的变化存在不合理跳跃[16-18],且并不能反映土壤中初始水分条件的实际变化,限制了SCS-CN模型径流预测的准确性[19-21]。为解决这些问题,众多学者结合不同地区土壤特征对SCS-CN模型的CN进行了修订和优化。其中,Mishra等[22-23]提出了一个基于前5日降水和土壤湿度计算土壤潜在蓄水量的SCS-CN模型,改善了CN的变化存在不合理跳跃的问题;Michel等[24]指出了作为原SCS-CN模型基础的土壤水分核算(Soil Moisture Accounting,SMA)结构中的几个不合理之处,指出了SCS-CN模型应该用初始土壤水分作为特征值,并对SCS-CN模型进行了结构和参数的改进,提出了MSCS-CN模型,但其研究仅提出了初始土壤水分的概念,并未对初始土壤水分作公式说明;在分析了Michel等[24]研究的缺点之后,Singh等[25]基于径流系数和饱和程度的概念提出了一种结构化更合理、稳定性更强的MMSCS-CN模型,并应用前几日降水量估算初始土壤水分。但无论是原SCS-CN模型,还是改进的模型对土壤前期水分条件的考虑都基于前几日降雨,并不能反映土壤中水分变化的真实情况。
降雨历时是降雨-径流过程的重要组成部分,对径流量的模拟有很大影响[3,5,19,26-27]。但SCS-CN模型中只考虑降雨量作为地表径流计算依据,未考虑降雨历时的影响,这导致径流预测的不确定性[5]。其主要原因是,降雨历时与降雨下渗量在次降雨事件中的呈正相关关系,这造成了SCS-CN模型在径流的模拟中对下渗部分水量计算的缺失。Wang等[5]发现初损率也随降雨历时的变化而变化,进而影响SCS-CN模型的径流模拟。Jain等[28]提出了一种基于降雨历时因子调整的降雨量输入的方法;Sahu等[29]将降雨历时结合下渗过程纳入到SCS-CN模型,提高了模型的预测效率,并被后人所参考,提出了一些改进的模型[30];Shi等[18]提出了一种基于降雨历时的经验方程用以修正系数CN,提高了模型准确度,而且没有增加其他参数。虽然这些研究提高了径流模型的准确性,但没有考虑前期水分条件对于降雨下渗的影响。
密云水库位于北京东北部,是北京市地表饮用水源地。在南水北调政策实施前,由于气候变化和人类活动,该水库的河流流量已大幅减少[31]。近年来,一些学者利用SCS-CN模型预测本区的地表径流量[32-33],也有一些学者将SCS-CN模型与其他模型结合起来用作非点源污染模拟的研究[8],还有一些学者根据密云水库上游潮白河流域的实际情况,对SCS-CN的模型应用进行了适用性改进。其中,焦剑等[34]采用最大30 min降雨量与次降雨量的比值反映次降雨在时间上集中程度,修正了CN;Pang等[14]考虑了坡度和降雨强度对潮白河流域CN的影响,建立了SWAT-CH模型并进行了测试。而现有研究在密云水库上游潮白河流域的山区应用SCS-CN模型时,并未考虑前期雨量和降雨历时对模型应用的影响。
本文为了改善原有的SCS-CN模型对初始水分条件及降雨历时响应不足的问题,提出一种基于前期水分条件和降雨历时改进的SCS-CN模型,并将本文改进的模型与SCS-CN模型、Singh的模型[25]及Shi的模型[18]作性能比较。本研究以北京市密云县石匣小流域为例,利用小流域内径流试验小区2006—2010年及2014—2020年的长期坡面径流观测资料作为模型校准及验证数据,研究结果可以为密云水库上游潮白河流域地表径流量的预测及区域水土流失监测评估中的应用提供参考。
1 数据来源与方法
1.1 研究区域及数据来源
研究区为位于北京市密云区密云水库上游的潮白河流域的石匣小流域,地理坐标为117°01′~117°07′E、42°32′~42°38′N,总面积约33 km2。为土石质浅山丘陵区,北部地势高,南部地势低,海拔在141~385 m,相对高差244 m,大于20°的坡面面积仅占全流域的16.2%。石匣小流域内的土壤类型多为在洪冲积物上发育的淋溶褐土,土层较深厚,质地为沙质土壤,容易漏水漏肥。气候上属暖温带季风气候,多年平均降雨量为661.8 mm,降雨多集中在夏季,其中6—8月份的降雨量占全年降雨量的76.5%。
石匣径流试验小区设在石匣小流域内,中心示范区面积为2 km2(图1)。径流小区位于石匣小流域的南部,坡度从3.5°~27°不等,土壤种类均为褐土,基岩种类基本为花岗岩,平均土层厚度为24 cm。各坡面小区土壤pH值平均6.272,裸地、耕地有机质平均为14.78 g/kg,草地、林地有机质平均为25.55 g/kg[34]。
在本研究中,数据采用石匣径流试验小区2006—2010年及2014—2020年的次降雨、气象水文观测数据,具体包括12年间连续观测的逐日降雨量、流域内4个不同土地利用类型试验坡面小区每场降雨的产流量及降雨历时(各小区12年间的产流量样本数见表1)。

表1 径流小区基本情况
1.2 降雨-径流特征分析
1.2.1 降雨特征
2006—2010年、2014—2020年间,石匣径流小区共有520场记录降雨,其中有117场降雨事件产生径流。对117次产流降雨的次降雨特征值(降雨场次、降雨量、降雨历时、平均雨强)进行分析(表2)。将117次降雨按照雨量大小进行分析(图2a),降雨量主要分布在10~30mm;按照降雨历时分布长短进行分析(图2b),降雨历时主要分布在1~12h。
1.2.2 降雨雨型划分
通过对降雨因子进行筛选分析,本文选择降雨量、降雨历时和降雨强度3个降雨因子,利用SPSS软件的聚类分析模块,采用K-均值聚类对117次降雨进行了不同降雨雨型的划分,并对每一种降雨雨型的特征值进行统计分析。
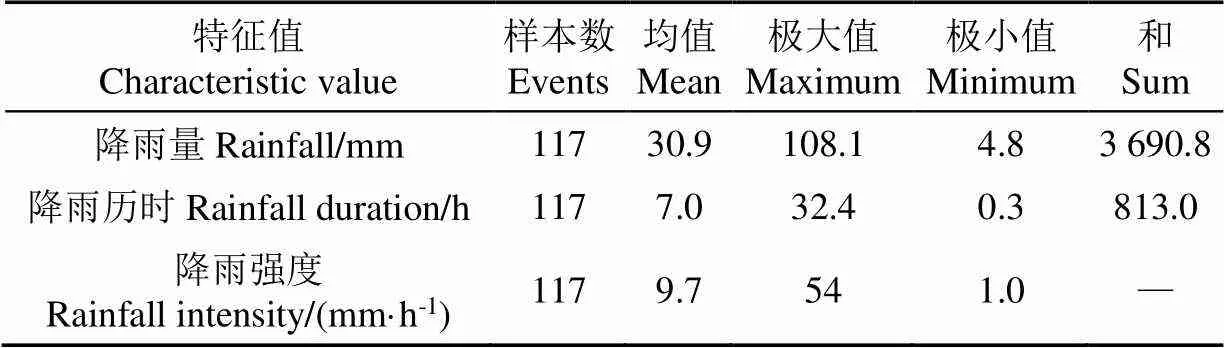
表2 降雨特征值统计表
通过聚类分析,将117次降雨事件分为3个降雨雨型分别以降雨雨型Ⅰ、降雨雨型Ⅱ、降雨雨型Ⅲ,各降雨雨型特征值如表3所示。降雨雨型Ⅰ为降雨历时短,降雨量小,降雨强度高、低频率的一类降雨事件;降雨雨型Ⅱ为降雨历时中等,降雨量较小,降雨强度低、高频率的一类降雨事件;而降雨雨型Ⅲ则是降雨历时长,降雨量大,降雨强度中等、较低频率的一类降雨事件。从所占的比例来看,本地区以降雨雨型Ⅱ即降雨历时中等,降雨量小,小雨强的降雨类型为主要产流降雨。
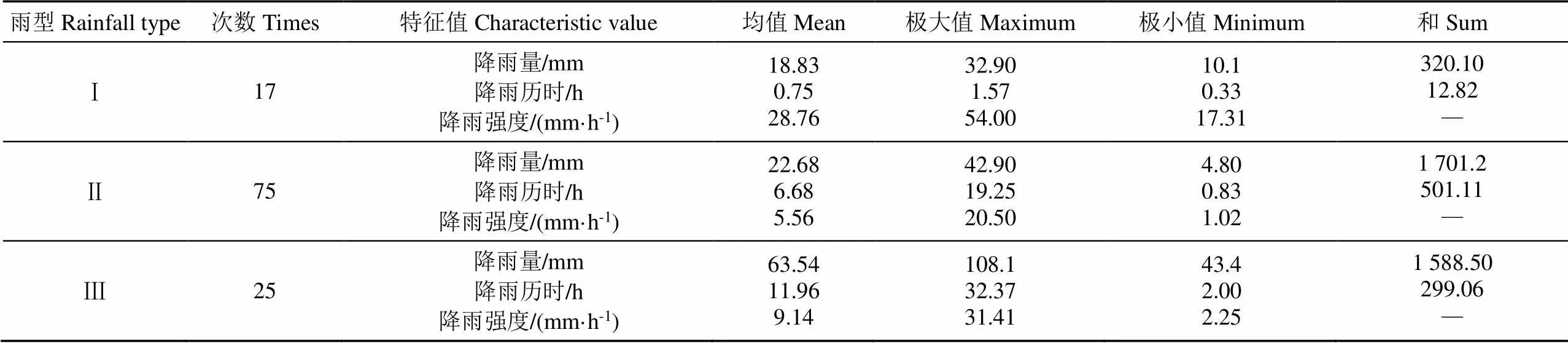
表3 不同降雨类型的统计学特征
1.2.3 径流深分组
为了探究不同径流深对本文改进的模型模拟结果的影响,利用SPSS软件的聚类分析模块,采用K-均值聚类对200次径流进行了不同径流深的分组。其中高径流深(29.65~37.34 mm)4例,中径流深(9.94~18.08 mm)46例,低径流深(0.49~9.04 mm)150例。从所占比例来看,本地区以低径流深为主要产流。
1.2.4 前期土壤水分分组
为了探究不同土壤水分条件对本文改进的模型模拟结果的影响,利用SPSS软件的聚类分析模块,采用K-均值聚类对200次径流产生前的土壤前期雨量进行了分组,土壤前期雨量根据API计算得出。其中湿润(92.62~166.62 mm)35例,正常(50.37~88.03 mm)85例,干旱(6.55~49.38 mm)80例。从所占比例来看,本地区产流的土壤水分条件以正常和干旱为主。
1.2.5 产流的降雨因子筛选
径流量与形成该径流量的雨量及其他影响因子(如降雨强度、前期土壤水分条件等)之间存在着相关关系。利用统计分析方法中的偏相关分析法,通过控制其他降雨因子,来分析某一降雨因子和径流的相关性,从而可以在排除其他因子影响的条件下,准确地判断该因子对径流的影响程度。
降雨量是影响地表径流的直接输入因子,降雨历时和降雨强度直接影响地表产流方式的变化,降雨强度随降雨时间而变化,不同降雨强度导致不同时间的产流方式。因此,在次降雨过程中,由于降雨量、降雨持续时间和降雨强度的不同,产生超渗流、蓄满流等不同的产流方式,最终影响地表径流量的大小。
对各降雨因子(降雨量、降雨历时、平均雨强)与坡面径流量进行偏相关分析(表4)。在控制其他变量条件下,径流量和降雨量表现出了极其显著的正相关关系;其次为降雨历时,表现为极其显著的负相关关系,与降雨强度相关性较差。由此可见降雨量和降雨历时这两个因子是影响坡面产流的重要因子。

表4 径流量与影响因子的偏相关分析
Note:*0.01<<0.05;**0.001<<0.01;***<0.001.
1.3 现有模型及改进
1.3.1 SCS-CN方程
SCS-CN模型中反应降雨与径流关系的SMA公式为
式中为径流开始时的实际蓄水量(mm);为土壤潜在蓄水量(mm);为一次降雨实际产生的地表径流量(mm),为总降雨量(mm);初损量I是地表径流开始前的降雨初损量(mm)。
实际蓄水量计算公式为
降雨初损量I为截流、填洼、渗透过程所损失的降雨量。与土壤潜在蓄水量之间存在一定的关系
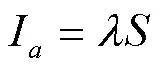
式中为降雨初损率,美国水土保持局在经过对大量长期的试验结果进行分析得出值为0.2。
将三式联立得SCS-CN模型计算公式
式中一般由研究区域实地监测数据获得;CN是为了计算引入一个参数——径流曲线数,与CN的关系式为
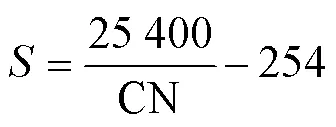
式中CN是一个无量纲参数,综合反映土地利用方式、土壤类型及前期产流条件(Antecedent Moisture Condition),范围在1~100之间,其值越大表明其蓄水能力越小。
SCS-CN模型根据土地利用方式的不同,将下垫面分为水体、裸地、草地、林地、耕地、居民地等种类;将土壤按最小下渗率分为A、B、C、D四组;根据前5日降雨总量将前期土壤湿润程度划分为干旱(AMCⅠ)、正常(AMCⅡ)、湿润(AMCⅢ)3个等级[34]。CN值可以通过美国国家工程手册[35]中的CN值表根据土地利用方式、土壤类型及前期土壤湿润程度进行查算。
1.3.2 Singh的模型
Singh等[25]在前人研究[24]的基础上对之前原SCS-CN公式的基础公式,SMA公式做出了改进,即公式(1)改进为下式
式中0为前期土壤水分(mm)。模拟径流量的模型也由原SCS-CN模型的公式(4)改进为下式
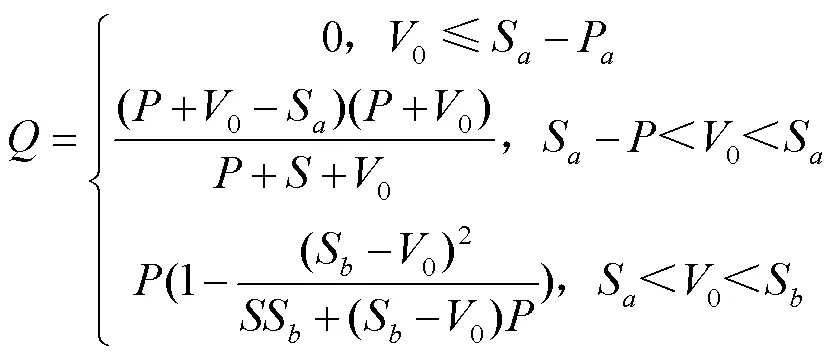
式中S是开始土壤水分,等于(0+I)(mm);S是绝对最大蓄水能能力,等于(+S)(mm)。S和0的值可以根据Mishra等[36]研究的方程计算
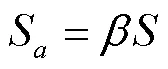
式中5为前5日降水量(mm);和是相关系数(无量纲),可以用回归分析来确定[28]。
1.3.3 Shi的模型
Mishra等[37]研究表明,累积渗透由静态渗透F和动态渗透F组成,并提出了新的SMA方程
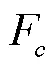
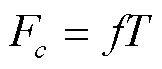
式中为静态渗透速度(mm/h),可以用回归分析来确定[28];是观测的降雨历时(mm)。
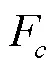
模拟径流量的模型也由原Singh等[25]所提出的模型的公式(4)改进为下式
1.3.4 基于前期雨量和降雨历时对SCS-CN模型改进
Huang等[38]根据土壤顶部15 cm处实测土壤水分,建立了一个非线性方程,该方程能更好地预测径流。Jennifer等[39]利用遥感获得的土壤数据估测,径流预测精度较原来有显著提高。然而土壤含水量数据获取较为困难,因此,本文通过前期雨量来表达研究区内土壤水分条件。
前期雨量是指某一降雨事件发生前降水的下渗量,前期雨量影响其径流产量[40-41]。API是基于降雨量、径流量、蒸发量、土壤水分再分配量等基本指标来构建简单的数学模型,通过模型模拟的手段来定量评价土壤水分状况。樊登星[42]用首都圈森林生态站实测的降雨和土壤水分资料,在前人研究基础上[43-44]构建了北京山区适用的前期降雨指数API模型
式中0为第天的前期降雨指数;为土壤水分消退系数,在北京山区夏季多雨季节时取0.95[42];(t-d)为第天的前天即前-天的前期降雨指数;(t-d)为前-天的降雨量;(t-d)为前-天的地表径流量。一般取30。
在前人对SCS-CN模型的降雨历时因子改进中,有些在对降雨量[28]或CN值[1]进行降雨历时因子的修正,有些并未考虑土壤前期雨量及降雨的土壤入渗量对静态渗透速度的影响[9,18]。这些改进不能反映出降雨历时对径流量的真实影响:相同降雨量的产流事件中,越长时间的降雨历时将会导致更长的下渗时间,更多的由下渗导致的径流损失量;而相同降雨历时的产流事件中,土壤前期雨量和降雨的土壤入渗量越多会导致更快的静态渗透速度越快,更多的由下渗导致的径流损失量。
Suresh等[19]在前人的研究基础上[28],提出了潜在最大蓄水S(mm)等于(+0),在特定流域时为固定值。
对于以上考虑,本文提出改进的SCS-CN模型
式中0=0,可以由式(14)计算得出;I可以由式(3)计算得出;S可以用回归分析来确定[28],F的值在考虑到次降雨事件中土壤前期雨量和降雨土壤入渗量后,可以根据以下方程计算
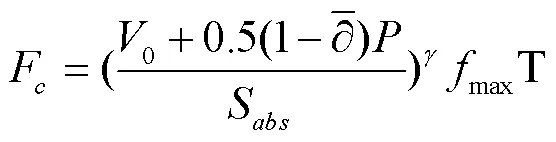
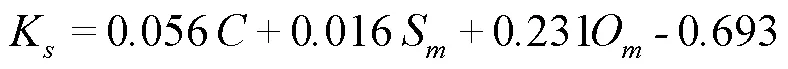
式中K代表饱和导水率(mm/min);表示土壤中黏粒含量(%);S是土壤中砂粒含量(%);O是土壤中有机质含量(%)。其中的土壤粒级分类标准依照美国制。
1.4 参数的确定
为了应用上述4种模型,将坡面小区的可用数据集分成两部分,其中一半用于校准,另一半用于验证。其中校准组和验证组的选择不是随机的,根据实测径流值,对数据进行降序排序,以保持校准和验证数据集中的水文均匀性,然后采取交替的降雨-径流值进行校准和验证[28]。采用Marquardt约束最小二乘算法确定各种模型的参数[46](表5)。
1.5 模型有效性的评价和验证方法
为了验证模型径流模拟精度,选用决定系数2、纳什效率系数NSE[47](Nash-Sutcliffe Efficiency coefficient)和均方根误差(Root-Mean-Square Error,RMSE)作为评价指标,其计算公式为
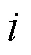
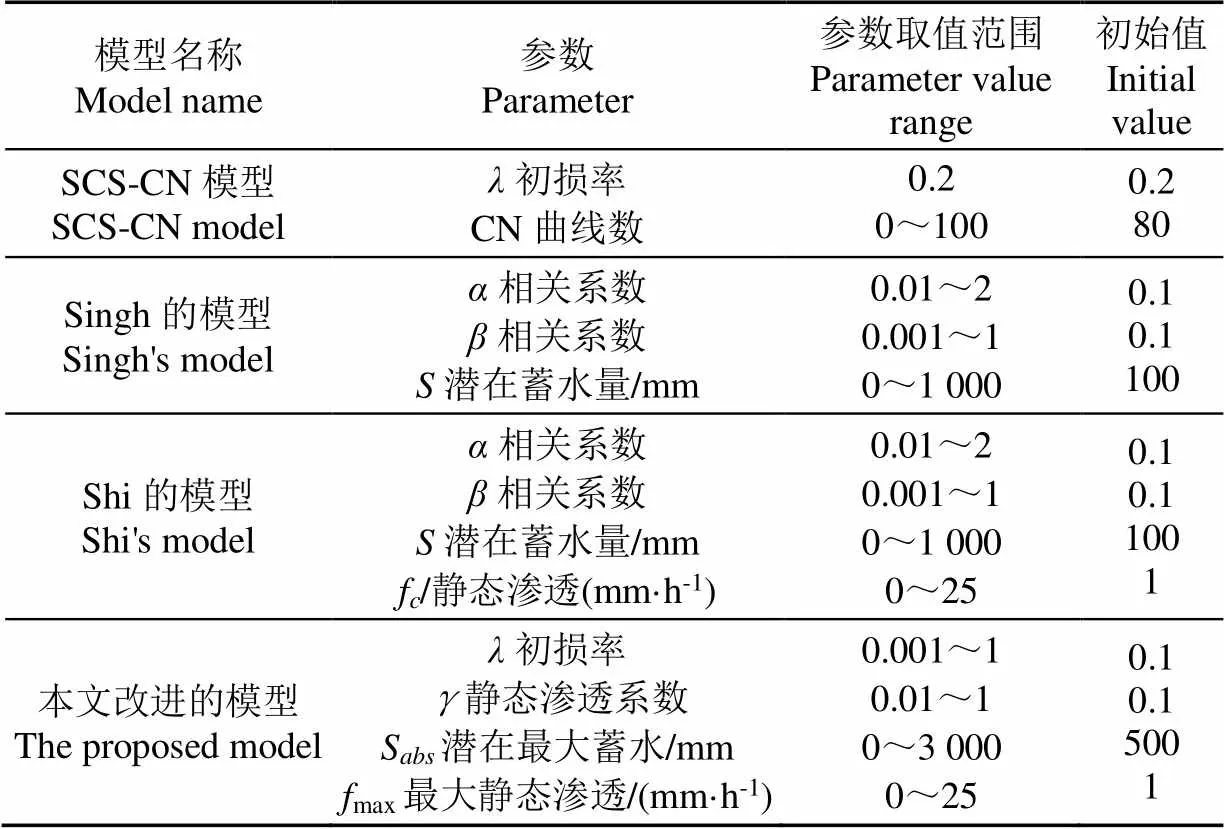
表5 四种模型需要优化的参数
2 结果分析
在石匣中径流小区收集的降雨径流事件中,用于校准和验证的降雨径流事件数分别为100和100。表6列出了采用校准数据集经过Marquardt约束最小二乘算法确定的参数。表7比较了基于统计指标的所有测试模型的总体性能。4种产流模型应用校准数据集和验证数据集计算的径流深对比如图3所示。应用完整数据集时,4种模型按不同实测径流深分组的平均相对误差(Mean Relative Error,MRE)如图4所示。
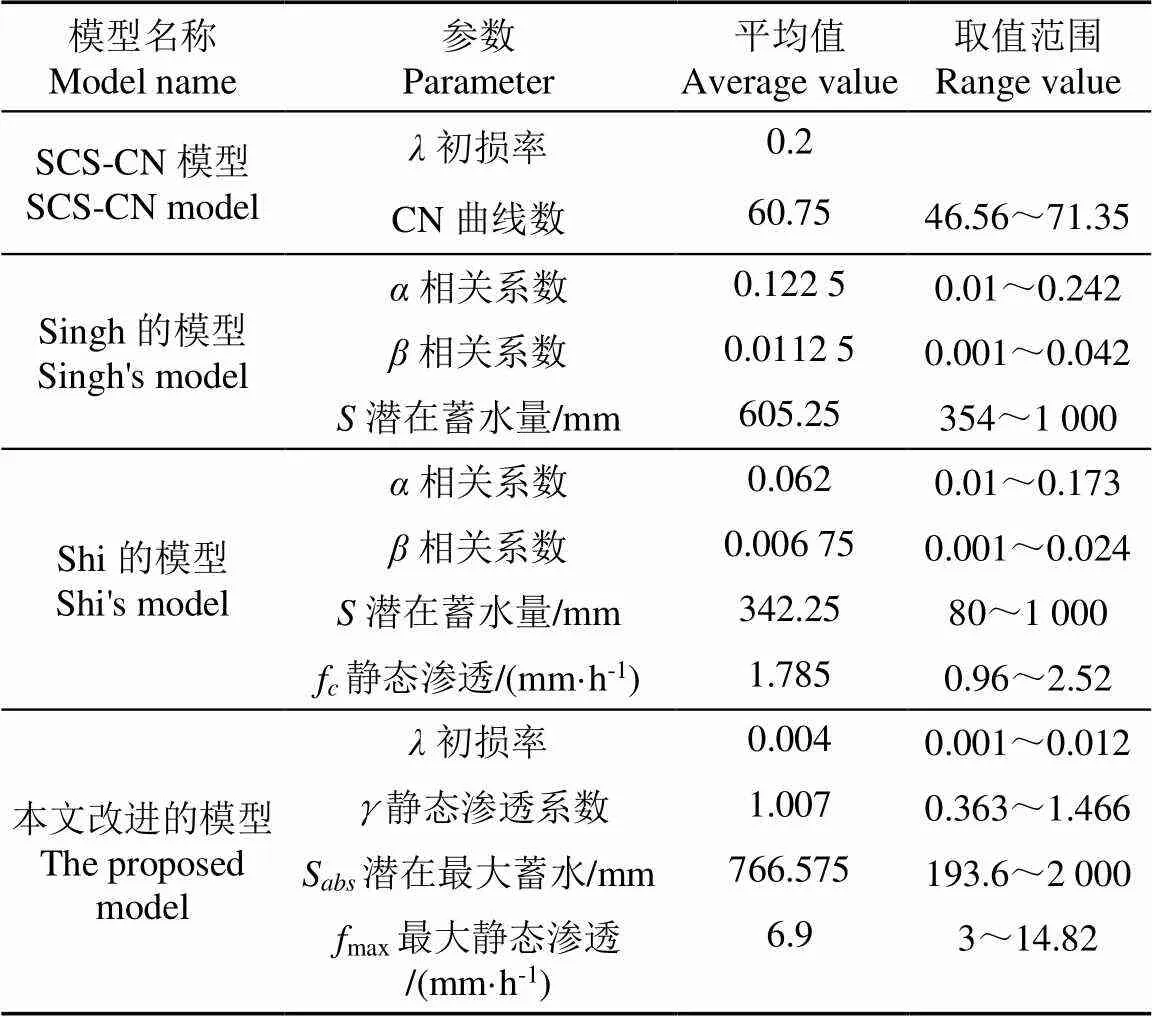
表6 四种模型参数优化结果
图3a~3d分别显示了SCS-CN模型、Singh的模型、Shi的模型和本文改进的模型在校准数据集、验证数据集和完整数据集中应用得到的径流实测值和相对应的径流模拟值的分布。在模型的回归直线与1∶1线重合度上,Singh的模型和Shi的模型表现较好,SCS-CN模型表现较差,本文改进的模型的模拟值和实测值的回归直线与1∶1线重合度极高,几乎与1∶1线重合。根据图4可知,SCS-CN模型较大程度地低估了低径流深的产流,对中径流深和高径流深的产流模拟结果的低估程度较小。Singh的模型较大程度地低估了高径流深的产流,对低径流深和中径流深的产流模拟的低估程度较小。Shi的模型较小程度地高估了高径流深度的产流,较小程度地低估了低径流深的产流,对待中径流深的产流几乎没有趋向性。在应用完整数据集的本文改进的模型较小程度地高估了低径流深度的产流,较小程度地低估了中径流深的产流,对待高径流深的产流几乎没有趋向性。与其他3种模型相比,本文改进的模型在全径流深的模拟表现上具有更高的稳定性,不会因为径流深而产生较大地趋向性误差。
在应用完整的数据集时,SCS-CN模型、Singh的模型、Shi的模型分别低估了200个降雨径流事件中的径流深169个、147个和121个,低估占比分别为84.5%、73.5%和60.5%,MRE则分别为0.25%、12.48%和2.67%。本文改进的模型的低估次数和高估次数基本持平,模型的MRE为0.06%。根据4种模型在评价指标NSE、2和RMSE的表现,本文改进的模型在3种指标评价均表现最好,Shi的模型性能较好,Singh的模型性能一般,SCS-CN模型性能最差。说明本文改进的模型在模拟精度、拟合度和误差上都优于其他3种模型。在应用完整数据集时,本文改进的模型的NSE、2相比于SCS-CN模型分别提高了319%、97.5%,而RMSE降低了107.5%。上述结果表明,在北京山区预测地表径流量时,若不考虑降雨历时和前期雨量的影响,会造成较大的预测误差。本文改进的模型在密云水库上游潮白河流域的降雨径流模拟中,表现优于SCS-CN模型、Singh的模型和Shi的模型,具有一定的适用性。
3 讨 论
总体而言,4种SCS径流模型的模拟结果都会低估径流,这与前人研究相符[49],而本文改进的模型比原有模型的低估情况有较大改善。分析其原因,可能是根据前期降雨指数对土壤前期水分条件的模拟要好于另外3种SCS-CN径流模型,另外3种SCS-CN径流模型对发生更早的强降雨事件对土壤水分条件影响的响应不足,低估了土壤前期雨量。SCS-CN模型和Singh的模型对局地强对流的短时强降雨事件的静态渗透响应不足,未考虑降雨历时较短,静态渗透总量较少,导致低估产流;而Shi的模型未考虑到雨季雨量爆发时长时间土壤水分大幅度增加的情况,这种条件下静态渗透速度变快,静态渗透总量变多,径流的静态渗透损失变多,此时模型高估了高径流深的产流。
在一般情况下,应用校准数据集时模型的模拟结果应该好于应用验证数据集时模型的模拟结果。但在此次研究中,应用验证数据集的SCS-CN模型和Singh的模型模拟结果都明显好于应用校准数据集的模型模拟结果。这可能是数据量较少或者是验证数据集径流量较小造成的,而SCS-CN模型和Singh的模型容易低估径流深造成的。
3.1 改进后的SCS-CN模型影响因素分析
对影响本文改进的SCS-CN模型模拟效果的主要因素进行了分析。首先,分析了应用完整数据集的本文改进的模型对于不同土地利用类型条件下降雨径流事件的模拟效果(图5a)。本文改进的模型对于裸地的产流模拟结果最好,耕地、林地的模拟结果一般,草地的模拟结果最差。裸地条件下模型的NSE为0.82,2为0.84;耕地NSE为0.65,2为0.70;林地NSE为0.62,2为0.62;草地NSE为0.85,2为0.09。
其次,分析了本文改进的模型对于不同降雨类型的模拟结果(图5b)。本文改进的模型对于降雨类型为雨型Ⅱ和雨型Ⅲ的模拟结果较好,雨型Ⅰ的结果模拟较差。降雨类型为雨型Ⅰ时,模型的NSE为0.11,2为0.84;降雨类型为雨型Ⅱ时,模型的NSE为0.56,2为0.77;降雨类型为Ⅲ时,模型的NSE为0.76,2为0.78。
最后,分析了本文改进的模型对于不同土壤水分条件的模拟效果(图5c)。本文改进的模型对于土壤水分条件为湿润的模拟结果较好。其中在土壤水分条件为湿润时,本文改进的模型的NSE为0.82,2为0.81;正常时NSE为0.73,2为0.78;干旱时NSE为0.76,2为0.77。
土壤水分条件为正常的平均径流深较小,为6.03 mm,而土壤水分条件为湿润及干旱的径平均流深分别为7.03和7.63 mm。降雨类型为Ⅰ的平均径流深较小为3.79 mm,降雨类型为Ⅱ和Ⅲ的平均径流深为5.03和12.45 mm。对所有实测-模拟的相对误差的绝对值与实测径流深进行相关性分析,实测-模拟的相对误差的绝对值与实测径流深呈-0.134的相关关系,=0.03。说明本文改进的SCS-CN模型的模拟效果与产流量呈正相关。产流较小,也是本文改进的模型对于土壤水分条件为正常、土地利用类型为草地和降雨类型为Ⅰ的降雨径流事件的产流模拟结果较差的原因。草地坡面的产流次数较少,校准参数的校准集的数据较少,也是草地条件下模型模拟效果较差的原因之一。
3.2 敏感性分析
敏感性分析可以区分出对本文改进的模型应用更敏感的参数,并且可以探究本文改进的模型的鲁棒性。因此,在本研究中,对校准的参数值进行变化,以观察应用完整数据集时,参数值变化对径流模拟NSE评价的影响。
图6展示了所提出的模型参数的敏感性分析,其中模型效率随参数而变化。可以看出,潜在最大蓄水和静态渗透系数是最敏感的参数,最大静态渗透速度的参数敏感性一般,初损率的参数敏感性最差。
在对本文改进的模型进行的敏感性分析中,可以发现本文改进的模型对参数敏感性极低,这与前人相关研究一致[18],并且对以后的模型应用中参数的存在合理性提出了质疑。
4 结 论
本文基于前期雨量和降雨历时改进了SCS径流流模型。引入了前期降雨指数模拟前期雨量,并根据潜在最大蓄水与前期雨量的差值估计潜在蓄水量;考虑了土壤前期雨量和次降雨事件中土壤入渗量对静态入渗的影响,修正了模型中的静态入渗部分。本文改进的模型应用完整数据集时的纳什效率系数为0.77,决定系数为0.79,均方根误差为3.21 mm,相比于SCS-CN模型纳什效率系数、决定系数分别提高了319%和97.5%,均方根误差降低了107.5%。本文改进的模型的可靠性相比于SCS-CN模型、Singh的模型和Shi的模型更好,在密云水库上游潮白河流域的降雨径流模拟中具有一定的适用性,同时可为其他地区的产流计算提供参考依据。本文改进的模型在受产流前降雨、蒸散发或渗透影响比较明显的地区使用更具优势。
径流深越高本文改进的模型性能表现越好,且未考虑雨强和坡度等因素对模型的影响,这在一定程度上会影响模型精度,导致在低径流深的径流模拟结果并不能让人完全满意。但在洪涝灾害预警及水土保持防治的实际工作中,耕地与裸地在湿润条件下且降雨历时长,降雨量大,降雨强度中等的高径流深的径流模拟才是关注重点。
[1] Shi W H, Wang N. An improved SCS-CN method incorporating slope, soil moisture, and storm duration factors for runoff prediction[J]. Water, 2020, 12(5): 1335.
[2] Al-Ghobari H, Dewidar A, Alataway A. Estimation of surface water runoff for a semi-arid area using RS and GIS-based SCS-CN method[J]. Water (Basel), 2020, 12(7): 1924.
[3] Kang M S, Goo J H, Song I, et al. Estimating design floods based on the critical storm duration for small watersheds[J]. Journal of Hydro-environment Research, 2013, 7(3): 209-218.
[4] Sahoo B, Chatterjee C, Raghuwanshi N, et al. Flood estimation by Giuh-based clark and nash models[J]. Journal of Hydrologic Engineering, 2006, 11(6): 515-525.
[5] Wang X X, Bi H X. The effects of rainfall intensities and duration on SCS-CN model parameters under simulated rainfall[J]. Water (Basel), 2020, 12(6): 1595.
[6] Darji K, Indra P, Binh T P. Runoff estimation of machhu and watrak rivers basins of Gujarat India using SCS-CN method and GIS[J]. Indian Journal of Ecology, 2020, 47(3): 726-732.
[7] Rajashekhar S L. Estimation of runoff using SCS-CN method for Yelahanka Region[J]. International Journal of Applied Engineering Research, 2018, 13(7): 229-233.
[8] 刘洁,庞树江,何杨洋,等. 基于小流域产流特征的磷流失关键源区识别[J]. 农业工程学报,2017,33(20):241-249.
Liu Jie, Pang Shujiang, He Yangyang, et al. Critical area identification of phosphorus loss based on runoff characteristics in small watershed[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(20): 241-249. (in Chinese with English abstract)
[9] Shrestha P M. Application of SCS-CN model in runoff estimation[J]. International Journal for Research in Applied Science and Engineering Technology, 2018, 6(3): 2363-2369.
[10] Chatterjee C, Jha R, Lohani A K, et al. Runoff curve number estimation for a basin using remote sensing and GIS[J]. Asian-Pacific Remote Sensing and GIS Journal, 2001, 14: 1-8.
[11] Phetprayoon T, Sarapirome S, Navanugraha C, et al. Surface runoff estimation using grid-based curve number method in the upper lam phra phloeng watershed, thailand[C]. Beijing: The 30th Asian Conference Remote Sensing , 2009.
[12] Caletka M, Šulc M M, Karásek P, et al. Improvement of SCS-CN initial abstraction coefficient in the czech republic: A study of five catchments[J]. Water (Basel), 2020, 12(7): 1964.
[13] Caletka M, Šulc M M. Determination of SCS-CN initial abstraction ratio in a catchment prone to flash floods[J]. Pollack Periodica, 2020, 15(1): 112-123.
[14] Pang S J, Wang X Y, Melching Charles S, et al. Development and testing of a modified SWAT model based on slope condition and precipitation intensity[J]. Journal of Hydrology, 2020, 588: 125098.
[15] Hawkins R. Asymptotic determination of runoff curve numbers from data[J]. Journal of Irrigation and Drainage Engineering-ASCE, 1993, 119(2): 344-345.
[16] Saini M, Karn A, Mishra S, et al. Evaluation of SCS-CN inspired models and their comparison[J]. Journal of Indian Water Resources Society, 2016, 36(3): 19-27.
[17] Verma S, Singh P K, Mishra S K, et al. Activation soil moisture accounting (ASMA) for runoff estimation using soil conservation service curve number (SCS-CN) method[J]. Journal of Hydrology, 2020, 589: 125114.
[18] Shi W, Wang N. Improved SMA-based SCS-CN method incorporating storm duration for runoff prediction on the Loess Plateau, China[J]. Hydrology Research, 2020, 51(3): 443-445.
[19] Suresh B P, Mishra S K. Improved SCS-CN–inspired model[J]. Journal of Hydrologic Engineering, 2012, 17(11): 1164-1172.
[20] Jiao P J, Xu D, Wang S L, et al. Improved SCS-CN method based on storage and depletion of antecedent daily precipitation[J]. Water Resources Management, 2015, 29(13): 4753-4765.
[21] Walega A, Amatya D M, Caldwell P, et al. Assessment of storm direct runoff and peak flow rates using improved SCS-CN models for selected forested watersheds in the Southeastern United States[J]. Journal of Hydrology: Regional Studies, 2020, 27: 100645.
[22] Mishra S K, Singh V. SCS-CN method. Part I: Derivation of SCS-CN-based models[J]. Acta Geophysica Polonica, 2002, 50(3): 457-477.
[23] Mishra S K, Sahu R K, Eldho T I, et al. An improved Ia-S relation incorporating antecedent moisture in SCS-CN methodology[J]. Water Resources Management, 2006, 20(5): 643-660.
[24] Michel C, Andréassian V, Perrin C. Soil conservation service curve number method: How to mend a wrong soil moisture accounting procedure?[J]. Water Resources Research, 2005, 41(2): 199-207.
[25] Singh P K, Mishra S K, Berndtsson R, et al. Development of a modified SMA based MSCS-CN Model for runoff estimation[J]. Water Resources Management, 2015, 29(11): 4111-4127.
[26] Kao S, Govindaraju R S. Probabilistic structure of storm surface runoff considering the dependence between average intensity and storm duration of rainfall events[J]. Water Resources Research, 2007, 43(6): W6410.
[27] Herath D. The discourse of development: Has it reached maturity?[J]. Third World Quarterly, 2009, 30(8): 1449-1464.
[27] 谷康民,赵允格,高丽倩,等. 黄土高原生物结皮对SCS-CN模型初损率的影响[J/OL]. 应用生态学报,2021,1-11:[2021-12-07]. https: //doi. org/10. 13287/j. 1001-9332. 202112. 005.
Gu Kangmin, Zhao Yunge, Gao Liqian, et al. Effects of biological soil crusts on the initial abstraction ratio of SCS-CN model in the Loess Plateau region[J/OL]. Chinese Journal of Applied Ecology, 2021, 1-11: [2021-12-07]. https://doi. org/10. 13287/j. 1001-9332. 202112. 005. (in Chinese with English abstract)
[28] Jain M K, Mishra S K, Suresh B P, et al. Enhanced runoff curve number model incorporating storm duration and a nonlinear Ia−S relation[J]. Journal of Hydrologic Engineering, 2006, 11(6): 631-635.
[29] Sahu R K, Mishra S K, Eldho T I. Improved storm duration and antecedent moisture condition coupled SCS-CN concept-based model[J]. Journal of Hydrologic Engineering, 2012, 17(11): 1173-1179.
[30] Shi W H, Huang M B, Gongadze K, et al. A modified SCS-CN method incorporating storm duration and antecedent soil moisture estimation for runoff prediction[J]. Water Resources Management, 2017, 31(5): 1713-1727.
[31] 庞树江,王晓燕. 密云水库流域入库径流量变化特征及归因研究[J]. 干旱区资源与环境,2016,30(9):144-148.
Pang Shujiang, Wang Xiaoyan. The characteristics and attribution of runoff change in the Miyun reservoir watershed[J]. Journal of Arid Land Resources and Environment, 2016, 30(9): 144-148. (in Chinese with English abstract)
[32] 张美华,王晓燕,秦福来. SCS模型在密云石匣试验小区降雨径流量估算中的应用[J]. 首都师范大学学报:自然科学版,2004(S1):155-158.
Zhang Meihua, Wang Xiaoyan, Qin Fulai. Application of SCS model to estimate the quantity of rainfall runoff of small watershed in Shixia, Miyun county[J]. Journal of Capital Normal University: Natural Science Edition, 2004(S1): 155-158. (in Chinese with English abstract)
[33] 何杨洋,王晓燕,段淑怀. 密云水库上游流域径流曲线模型的参数修订[J]. 水土保持学报,2016,30(6):134-138.
He Yangyang, Wang Xiaoyan, Duan Shuhuai. Revision of CN value and initial abstract ratio in the SCS-CN model in upper reaches of Miyun Reservoir[J]. Journal of Soil and Water Conservation, 2016, 30(6): 134-138. (in Chinese with English abstract)
[34] 焦剑,宋伯岩,王世雷,等. 基于改进径流曲线数模型的北京密云坡地径流估算[J]. 农业工程学报,2017,33(21):194-199.
Jiao Jian, Song Boyan, Wang Shilei, et al. Runoff estimation for hillslope land in Miyun based on improved model of soil conservation service curve number[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(21): 194-199. (in Chinese with English abstract)
[35] Service E. Hydrology[M]. Washington: United States Department of Agriculture, 1972.
[36] Mishra S K, Tyagi J V, Singh V P, et al. SCS-CN-based modeling of sediment yield[J]. Journal of Hydrology (Amsterdam), 2006, 324(1-4): 301-322.
[37] Mishra S K, Singh V P. SCS-CN-Based Hydrologic Simulation Package[M]. Colorado: Water Resources Publications, 2002.
[38] Huang M B, Gallichand J, Dong C, et al. Use of soil moisture data and curve number method for estimating runoff in the Loess Plateau of China[J]. Hydrological Processes, 2007, 21: 1471-1481.
[39] Jennifer M J, David A M, Brent M W. Improved rainfall/runoff estimates using remotely sensed soil moisture[J]. Journal of the American Water Resources Association, 2003, 39: 313-324.
[40] Ali S, Ghosh N C, Singh R. Rainfall–runoff simulation using a normalized antecedent precipitation index[J]. Hydrological Sciences Journal, 2010, 55(2): 266-274.
[41] Jiao P j, Xu D, Wang S l, et al. Improved SCS-CN method based on storage and depletion of antecedent daily precipitation[J]. Water Resources Management, 2015, 29(13): 4753-4765.
[42] 樊登星. 北京山区坡面土壤侵蚀响应特征及模型模拟研究[D]. 北京:北京林业大学,2014.
Fan Dengxing. Study on Slope Soil Erosion Response and Model Simulationin Beijing Mountainous Area[D]. Beijing: Beijing Forestry University, 2014. (in Chinese with English abstract)
[43] 卫伟. 典型黄土丘陵区降雨和下垫面综合作用下的水土流失效应[D]. 北京:中国科学院生态环境研究中心,2007.
Wei Wei. The Effect of Characteristics of Rainfall and Earth Surfaces on Runoff and Soil Erosion in the Typical Loess Hilly Area[D]. Beijing: Research Center for Eco-Environmental Sciences, 2007. (in Chinese with English abstract)
[44] 李琪. 黄土地区土壤含水量消退系数的变化规律与产流计算[J]. 人民黄河,1989,3(11):18-23.
w Li Qi. Regularity of variation of recession coefficient of autecedent precipitation in soil and runoff yield estimating for loess regions[J]. Yellow River, 1989, 3(11): 18-23. (in Chinese with English abstract)
[45] 符素华,王红叶,王向亮,等. 北京地区径流曲线数模型中的径流曲线数[J]. 地理研究,2013,32(5):797-807.
Fu Suhua, Wang Hongye, Wang Xiangliang, et al. The runoff curve number of SCS-CN method in Beijing[J]. Geographical Research, 2013, 32(5): 797-807. (in Chinese with English abstract)
[46] Marquardt D W. An algorithm for Least-Squares estimation of nonlinear parameter[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431-441.
[47] Nash J E, Sutcliffe J V. River flow forecasting through conceptual models part I-A discussion of principles[J]. Journal of Hydrology, 1970, 10(3): 282-290.
[48] Nearing M A, Liu B Y, Risse L M, et al. Curve numbers and Green-Ampt effective hydraulic conductivities[J]. Journal of the American Water Resources Association, 1996, 32(1): 125-136.
[49] 卜慧,邵骏,欧阳硕,等. 改进SCS模型在老挝南乌河流域中的应用[J]. 人民长江,2018,49(22):88-92.
Bu Hui, Shao Jun, Ou Yangshuo, et al. Application of modified SCS model in runoff calculation in Nam Ou Basin, Laos[J]. Yangtze River, 2018, 49(22): 88-92. (in Chinese with English abstract)
Improvement of SCS-CN model based on antecedent precipitation and rainfall duration
Wu Aipu1, Wang Xiaoyan1,2※, Huang Jieyu1, Huang Jingyu1, Wang Jun1, Li Zeqi1
(1.,,,100048,;2.,,100048,)
An accurate prediction of the runoff has been one of the important steps in the water supply in recent years. However, there is a sudden jump in the runoff prediction under the general configuration of Antecedent Moisture Condition (AMC) by Soil Conservation Service Curve Number (SCS-CN). At the same time, the rainfall duration cannot be considered as an important component of the surface runoff. Therefore, it is necessary to modify the prediction model of rainfall runoff for ecological and economic significance. Taking the Miyun reservoir in Beijing of China as the research object, this study aims to propose an improved SCS-CN model using antecedent precipitation and rainfall duration. A partial correlation analysis was first made between the rainfall factors (rainfall, rainfall duration, and average rainfall intensity) and slope runoff. The rainfall and rainfall duration were then selected as the important factors affecting the slope runoff in the study area. Subsequently, an updated SCS-CN model was established to combine with the early rainfall and rainfall duration. The Antecedent Prediction Index (API) was also used to simulate the soil’s early water conditions. A static infiltration equation was considered the soil early rainfall and infiltration in a rainfall event. Among them, the potential maximum water storage was equal to the sum of the previous soil moisture and the potential soil water storage. The maximum static infiltration rate was the static infiltration rate when the watershed soil moisture reached the full storage, and the static infiltration coefficient was dimensionless related to the soil structure and land use. The monitoring data was collected from the 200 rainfall runoff events in the runoff community of the Shixia basin from 2006 to 2010 and 2014 to 2020. The newly improved model was finally verified to compare with the original and two improved SCS-CN models. The results showed that the improved model performed best among the four runoff models, where the Nash efficiency coefficient was 0.77, the determination coefficient was 0.79, and the root mean square error was 3.21 mm. The Nash efficiency coefficient, the determination coefficient and increased by 319%, 97.5%, and root mean square error was reduced by 107.5% respectively, compared with the original SCS-CN model. Furthermore, the improved model was much better than the rest, where the four SCS runoff models had underestimated the runoff. It was found that the improved SCS-CN model was positively correlated with the yield. Nevertheless, the improved model was not suitable for the rainfall runoff events with the normal soil moisture, grassland land use type, and rainfall type I (short rainfall duration, small rainfall, high rainfall intensity, and low frequency). The parameter sensitivity analysis showed that the most sensitive parameters were the potential maximum water storage and static infiltration coefficient. Specifically, there was a general parameter sensitivity of the maximum static infiltration velocity, whereas, the initial loss rate was the worst. Consequently, the improved model presented strong applicability for the rainfall runoff of Chaobai River Basin in the upper reaches of Miyun reservoir. This finding can provide a strong reference basis for the calculation of runoff yield.
runoff; models; precipitation; SCS-CN model; antecedent-precipitation index; rainfall duration
吴艾璞,王晓燕,黄洁钰,等. 基于前期雨量和降雨历时的SCS-CN模型改进[J]. 农业工程学报,2021,37(22):85-94.doi:10.11975/j.issn.1002-6819.2021.22.010 http://www.tcsae.org
Wu Aipu, Wang Xiaoyan, Huang Jieyu, et al. Improvement of SCS-CN model based on antecedent precipitation and rainfall duration[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(22): 85-94. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2021.22.010 http://www.tcsae.org
2021-08-26
2021-10-29
北京市自然科学基金委员会-北京市教育委员会联合资助重点项目(KZ201810028047);国家自然科学基金项目(21377168;41271495)
吴艾璞,研究方向为水文模型与非点源污染。Email:313031400@qq.com
王晓燕,博士,教授,研究方向为农业非点源污染及流域水质管理。Email:wangxy@cnu.edu.cn
10.11975/j.issn.1002-6819.2021.22.010
S157
A
1002-6819(2021)-22-0085-10
