基于钻孔数据进行矿体克里金插值分析
2021-02-16刘亚静赵秀梅甘德清
刘亚静 ,赵秀梅 ,2,甘德清 ,2
(1.华北理工大学 矿业工程学院,河北 唐山 063210;2.河北省矿业开发与安全工程实验室,河北 唐山 063210)
0 引言
我国钨资源储量和生产量都居于世界第一,随着对钨需求量的增加,大规模的矿山开采给生态环境带来巨大的影响[1-2]。为了保障矿区的可持续发展,准确模拟矿区地下岩层的分布形态[3-4],李海港等[5]学者对钨矿进行三维建模可视化。由于离散钻探数据建立的曲面不能准确反映岩层的分布,需要确定精确的空间插值方法,利用最优插值方法,对矿区金属元素进行储量计算。
研究基于某矿区钻孔数据,使用GIS空间地质统计学和相关软件,分析数据特征[6-8],通过交叉验证方法,得到最优插值方法,为矿体储量计算提供了依据。以期为该矿山地理信息领域的进一步研究提供参考。
1 研究区数据基础
研究矿井样本点经整理共110个样本点数据,将结果整理为EXCEL表格数据。为了将EXCEL数据转换为属性特征表,使用ArcGIS的添加x,y数据工具进行转换,利用ArcGIS定义投影工具,建立相应的数据系统[9-10],得到钻孔的空间位置分布,如图1所示。

图1 矿区点分布Fig.1 Distribution of the mining area
2 矿区钻孔数据空间特征分析
2.1 地质统计学基础
克里金插值法又称空间插值,是一种基于变量理论和结构分析,对有限区域内的区域变量进行无偏最优估计的方法。采用已知样本点之间的距离和空间方位来反映空间相关性,对未知点进行线性无偏最优预计[11]。
克里金法插值公式如式(1)所示。
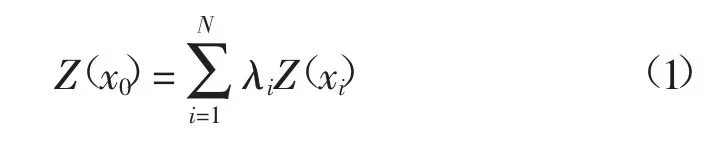
其中:λi为第i个样本点的未知权重;N是已知点的数目;Z(xi)为位置i的样本值;Z(x0)为未知样本值[13]。
2.2 空间数据分析
ArcGIS软件的地质统计学模块提供了许多功能,其中直方图法、正态QQ图法,趋势分析和半方差/协方差函数云可分析数据[12]。当获得样本点时,首先需要对数据进行分析,分析数据是否服从正态分布,是否存在趋势,检验数据是否合乎实际情况,剔除明显差异点。
2.2.1 矿井数据分布直方图和正态Q Q图检验
采用直方图法和正态QQ图法对110个样本点进行了分析,比较样本点数据对数变化前后的正态分布。由图2、图3可得,样本点数据经过对数变换后更符合正态分布。

图2 直方图Log变化后分布Fig.2 Histogram Log distribution after the change
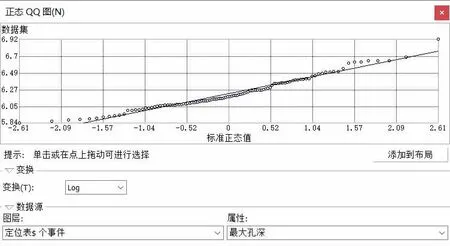
图3 正态QQ图Log变化后分布Fig.3 Log distribution after the change in the normal QQ chart
2.2.2 趋势分析
感兴趣区域的表面在各处出现渐变时,将该表面与采样点拟合,得到渐进趋势的平滑表面[11]。使用ArcGIS软件地质统计学模块中的趋势分析工具对数据进行处理,结果如图4所示,数据在X和Y方向上都呈二阶分布。更加直观地了解整个数据在区域范围内有较强的趋势变化。
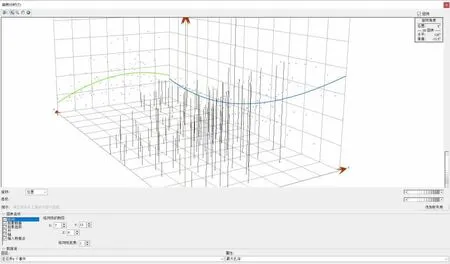
图4 矿区地质云数据趋势分布图Fig.4 Distribution of geological cloud data in the mining area
2.2.3 空间自相关
利用半变异函数的协方差云图对所得数据进行分析。其中,水平坐标反映的是两点之间的距离,而垂直坐标反映的是-1~+1之间的半变异值,区域化变量距离越近,相似性越大。结果如图5显示,半变异值主要集中在-0.45~+1之间,空间自相关较强。因此,可以得出该数据可用于克里金插值的结论。
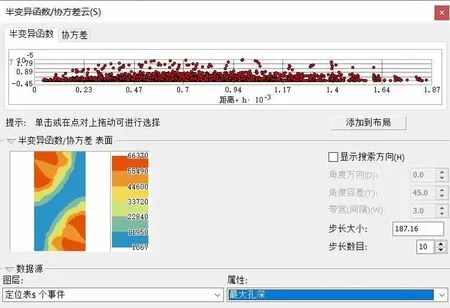
图5 半变异函数云图Fig.5 Semi-variogram cloud
3 比较不同空间插值选取最优插值方式
3.1 有效性评价
交叉验证是指从样本数据集中删除一点,使用其他样本值估计此点属性,并计算与实际值之间误差,重复以上步骤直到遍历所有采样点。在多种插值方法,多个参数之间选取最优方法,采用交叉验证来比较优劣。
交叉验证的参数包含多个误差,在本文采用了标准均值(SEM)、标准化均方根误差(RMSSE)、平均标准误差(ASE)、均方根误差(RMSE)和平均误差(ME)进行评估[14-15]。平均标准误差越接近于零,准确度就越高[14]。同时,RMSSE误差和SEM误差越小,精度越高。
3.2 分布趋势剔除
采用最常用的普通克里金插值法和简单克里金插值法,比较了常数、一阶和二阶趋势面与数据符合情况[15-17]。其中变量参数统一设置为高斯变异函数模型,步长数为12,模型类型为稳定,计算偏基台值为true,搜索邻域类型为标准工具,表1为误差结果。观察表1发现,普通克里金插值和简单克里金插值中,一阶趋势面ME、SEM、RMSSE误差较小,效果较好。因此,本研究基于一阶趋势面进行以下数据分析。
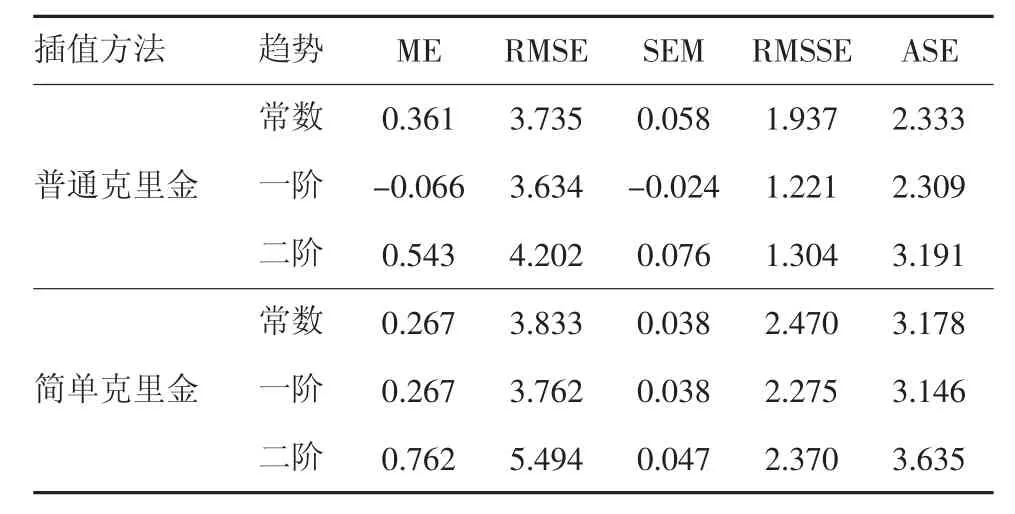
表1 趋势面阶数误差结果Tab.1 Order error results of the trend surface
3.3 克里金不同插值方法插值比较
3.3.1 普通克里金法插值分析
普通克里金法是一种线性克里金法,区域变量满足二阶平稳且期望为未知常数,较符合实际情况,应用范围较广。本研究的初始步长为6,间隔为3,最终步长为21。基于一阶趋势面,对样本数据进行对数变换,选择高斯、球面和指数模型。结果如表2,球面函数模型和指数函数模型的均方根误差和平均标准误差较大;高斯函数模型的平均标准误差最接近均方根误差,均方根误差最低。相比之下,高斯模型的均方根误差和平均标准误差都很小,因此选择高斯模型作为最优参数。
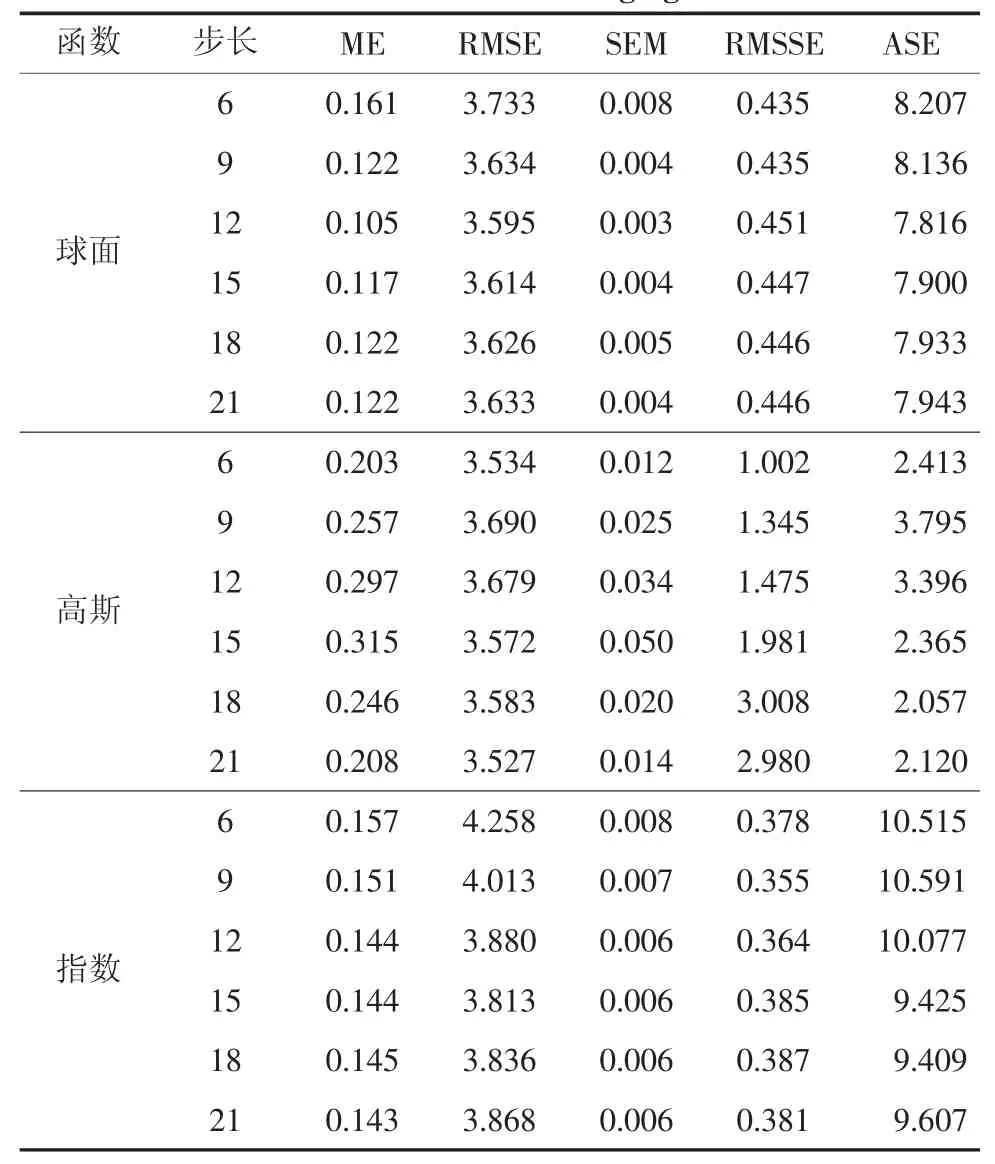
表2 普通克里金误差统计Tab.2 Statistics of the Kriging error
对高斯模型的不同步长数进行对比来确定最优步长数,要求各个误差值越小越好,结果如图6曲线所示。从图6对比结果可知,误差值都较低时,步长数为6,故确定步长数6为最优参数。
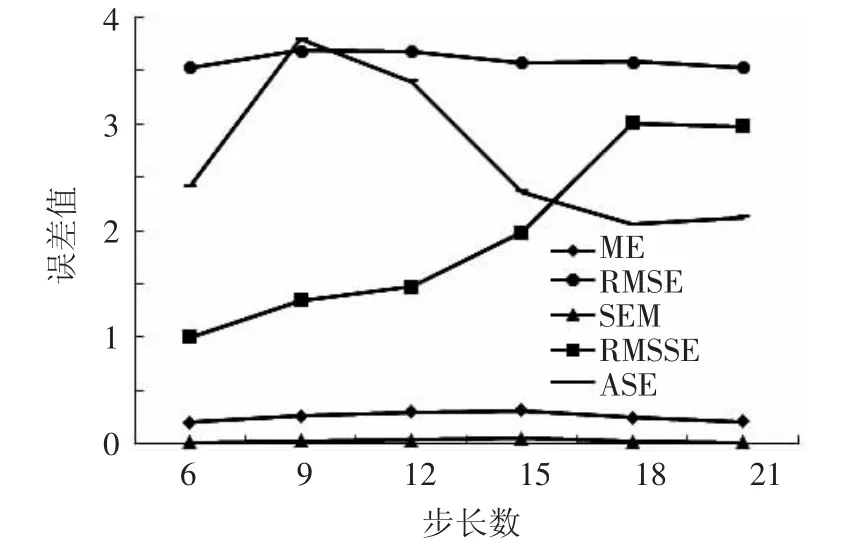
图6 普通克里金法插值误差曲线Fig.6 Interpolation error curve of ordinary Kriging method
3.3.2 简单克里金法插值分析
简单克里金法,区域化变量满足二阶平稳,期望值通常很难准确估计,估计值精度低。逐项比较误差的精度评定是一个复杂的过程,且含有不确定因素,因此定义4个评价指数S,V,W,Z,计算公式为:
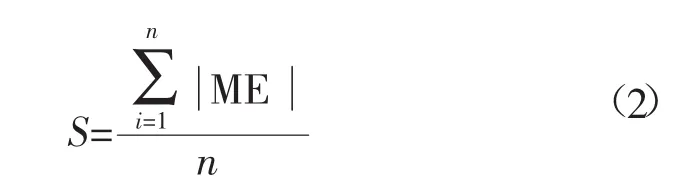
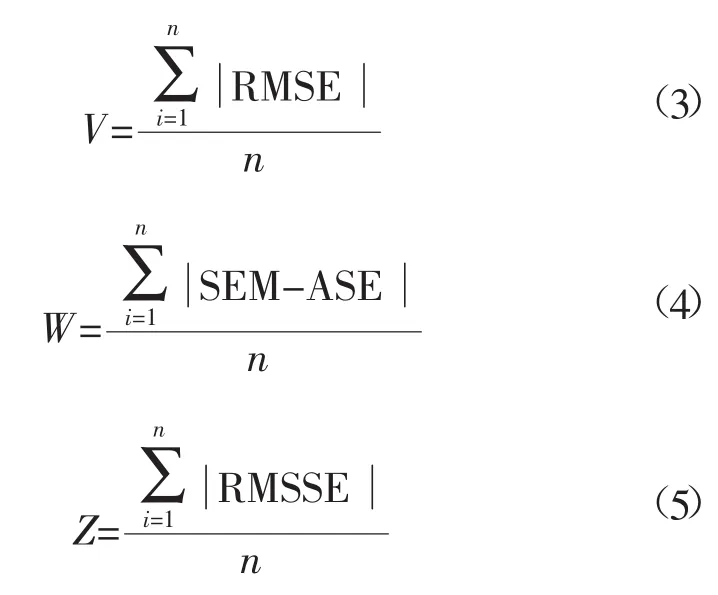
其中:n 代表步长数,S,V,W,Z 四个值越小代表插值精度越高。根据以上公式,简单克里金误差评价指数见表3。
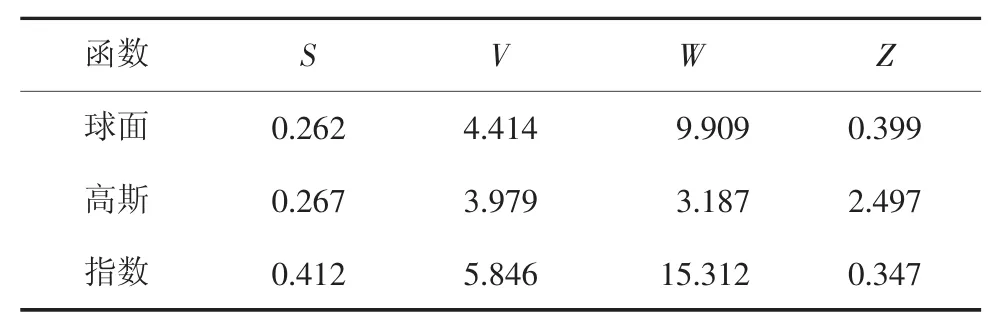
表3 简单克里金误差评价指数Tab.3 Error evaluation indices of simple Kriging method
综合比较,高斯球面函数模型,V和W评价指数相对较小,分别为3.979和3.187,精度更高,固选取高斯函数为最优模型。分析图7,当步长数为6,简单克里金法插值的误差相对较小,故确定步长数6为最优参数。
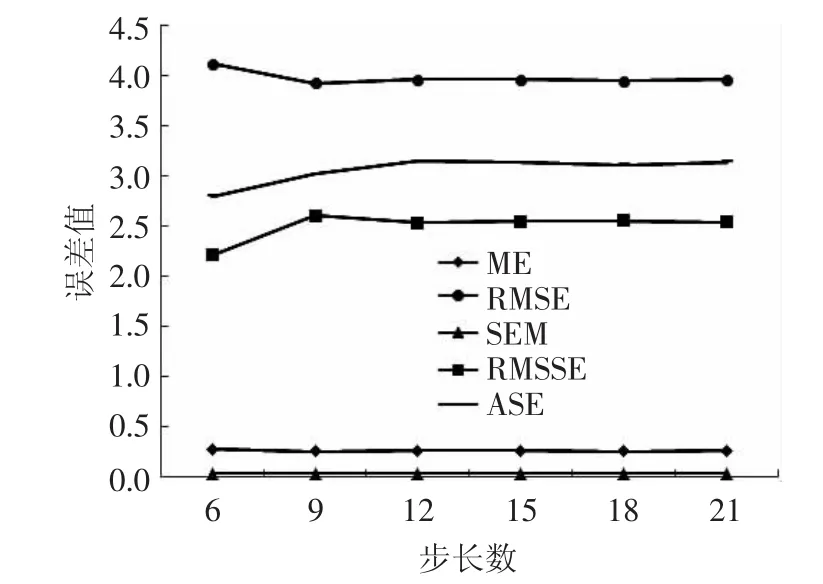
图7 简单克里金法插值误差曲线Fig.7 Interpolation error curve of simple Kriging method
3.3.3 两种方法插值结果比较
分析插值结果得到,当函数模型选取高斯,步长数为6,采用普通克里金和简单克里金两种方法进行插值结果分析,结果如表4。
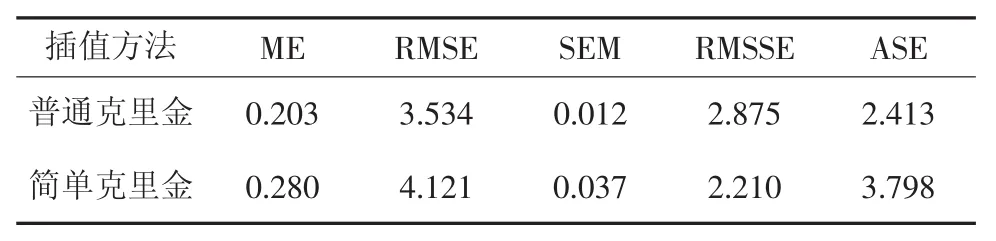
表4 高斯模型步长数为6时误差统计Tab.4 Error statistics of step number 6 in the Gaussian model
根据误差统计表分析,普通克里金法的ME、RMSE、SEM和ASE误差值都为最低,普通克里金方法插值效果最好。因此,文章选取高斯球面函数,步长数为6,普通克里金方法的空间插值方法最好。
4 三维可视化图
基于此数据,针对某矿体通过Surpac软件建立三维地质模型[18-20],有以下几个步骤:
(1)根据勘探线剖面图绘制各条勘探线的刨面;(2)将线状剖面图依次连接,形成三维矿体模型;(3)根据模型的坐标范围,建立三维模型的块体模型,建成块体模型如图8所示;(4)通过三角网对块体模型进行约束,并保持矿体的内部局限性,形成矿体约束模型;(5)对约束后的块体模型进行赋值;(6)赋值后的模型进行克里金插值,将不同品位区间赋予不同颜色。

图8 三维地质模型Fig.8 Three-dimensional geological model
在克里金插值中,考虑了信息样本的形状和大小、信息样本与待估块的空间分布位置以及品位的空间结构等主要几何特征。为了实现无偏、线性和精确的估计,对每个品位值进行赋值,然后用加权平均法估计区块品位。
将部分矿体模型进行克里金插值,不同品位值区间赋予不同颜色如表5,结果如图9所示。

表5 品位值区间与颜色对应表Tab.5 Grade value range and color coreespondence table
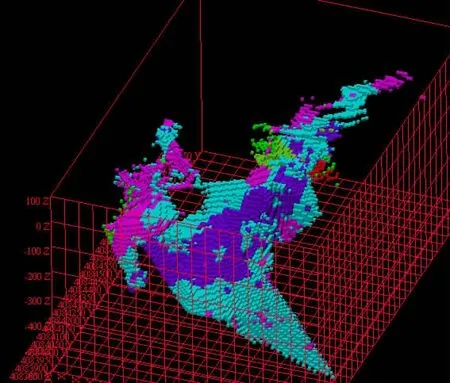
图9 矿体某金属元素品位分布Fig.9 Grade distribution of a metal element in ore body
从图9可以看到,矿体某金属元素品位值颜色分布情况,首先淡蓝色区域最大,接着是深紫色区域,然后是淡紫色区域。根据表5得到,该矿体某金属元素品位值范围在30%~60%之间,其中品位值在40%~50%的区域范围最大,为采矿提供了参考。
5 结论
研究基于实际钻孔数据,采用相关软件对数据进行了分析,得到最优插值方法,探索得到结论。
(1)对110个钻孔数据进行空间插值分析,从空间自相关的半变异函数云图中得到,数据集中在-0.45~+1的范围内,局部变量的间隔越近,相似度越大,说明数据可以用于克里金插值。
(2)从插值结果来看,当采用普通克里金,高斯函数模型,步长设置为6时,更能准确地反映地层的空间分布。
(3)通过建模,对模型进行克里金插值,将插值后的模型进行不同属性着色,更加直观地看出矿体元素品位值的分布。
