基于复杂网络理论的电网脆弱线路辨识

王 晶，赵浩渊，闫 涵，赵焕蓓，崔鹏羽

(1.国网青海省电力公司电力科学研究院，青海 西宁 810008；2.国网青海省电力公司西宁供电公司，青海 西宁 810008)

0 引言

随着社会发展，电网规模越来越大，电网发生故障的概率也越来越多，电网的故障反应能力、继电保护能力更加复杂，电网的脆弱性〔1〕问题也逐渐浮现出来。近年来，大型电力系统中断运行的故障时常出现，为了防止大电网事故发生，基于复杂网络理论研究整个电网的脆弱性具有深远的作用及影响。与此同时，研究人员也发现大规模停电事故最初通常只是少许元件故障,而事故增强过程与电网的脆弱线路关系很大。由此可见,辨识并加固电网中的脆弱线路可以大大增强电网的可靠性，对于减小大规模停电事故发生的几率也有非常深远的作用。

文献〔1〕以线路电抗值作为权重，并在此基础上提出最短电气距离和最短路径的定义。文献〔3〕〔4〕也将电抗定义为线路权重，与之不同的是，运行容量和运行极限要素也被加入到权重指标中，电抗值从不变过渡到可变的范围，更具有实际意义，以上两个要素的提出也开创了先河。除此之外，3篇文献分别从加权和无权的角度出发，对二者进行探讨，总结出加权网络比无权网络更能体现电力系统运行状况的结果。文献〔5〕分析了各区域功率的相互转化关系，求解到功率在各线路各节点间的转化途径以及传输规模，推测出系统行为。文献〔6〕提出并总结了拓扑图分区的方法，找到了连接子区域的脆弱线路，但是存在很难分辨单纯在特殊位置的线路的局限性。由此可见，如今有很多关于电网脆弱性的研究，却往往存在考虑不周的情况。本文结合已有的研究，针对线路提出了基于带权重线路介数的电网脆弱线路辨识的方法。

1 脆弱线路辨识方法

1.1 介数指标

复杂网络理论提出以下假定：任何两个节点间的信息根据节点间最短路径传送，节点或边沿最短路径通过的次数表征了此节点或边在信息传送中的重要度。介数通常分为节点介数和边介数两种，边介数定义为网络中两个节点之间最短路径或最有效路径中通过该边(线路)的数目和其两个节点间最短路径总数目的比值，即：

对于某一个无向无权网络M，E表示边集，边介数CB(e)的数学表达式就是：

(1)

其中：σij是节点i和节点j之间最短路径或最有效路径的数量；σij(e)是节点i和节点j之间最短路径或最有效路径中通过边e的数量。

为了更加合理有效地识别出电网的脆弱线路，本文在介数指标的基础上提出带权重线路介数指标。

1.2 带权重线路介数指标

发电机作为电网生产运行的关键一环，其容量及规模也应被纳入我们研究内容之中。在这样的前提下，我们定义了带权重线路介数BLW：

若线路(m，n)被发电机i与负荷j间最短电气路径经过，则该线路需承担发电机i带来的负载Wi。定义线路(m，n)的带权重线路介数BLW(m，n)为其因被网络中发电机与负荷之间的最短电气距离经过而承受的负载和。带权重线路介数指标定义如下：

(2)

其中：Ss为经过线路(m，n)的最短电气路径的发电机序号的集合。

1.3 脆弱线路辨识流程

为寻找到电网脆弱线路，针对本文提出的带权重线路介数，本文提出以下辨识流程：

1)针对以上建模方法对我们所研究的系统初步建立模型，最初求得连接权矩阵{Aij}和发电机权重矩阵{Wi}；

2)根据连接权矩阵{Aij}计算整个网络的最短电气距离矩阵{Dij}；

3)寻找任意发电机节点以及负荷节点间的最短电气路径集SL；

4)对最短电气路径集SL拆分，得出各小段线路指标，依据公式(2)得到各个线路的带权重线路介数BLW(m，n)；

5)对每条线路按带权重线路介数大小进行排序；

6)确定排序靠前的线路为脆弱线路。

1.4 脆弱线路辨识建模

对IEEE 39节点系统和青海电网俄博图电厂、宁北电厂附近区域的110 kV电网进行建模与简化，建模原则具体如下：

1)线路不考虑变电站母线以及电厂线路，简化线路拓扑图，同时保证准确度没有受到影响；

2)网络中所有节点分为3个集合，发电机节点集SG，负荷节点集SL，变电站节点集ST，分别有NG、NL和NT个；

3)任意线路都定义成无向且有权，线路的权重定义为线路的电抗值，并定义网络中任意两点间的最短电气路径为两点间所有路径中沿线线路权重和最小的路径，最短电气路径的沿线线路权重和为最短电气距离；

4)合并并联的同杆输电线，复杂的特殊情况忽略，使模型成为简单图。

发电机的权重Wi定义为发电机i在当前运行方式下的有功功率输出。

通过这样的方法建模后，电网就处理成一个有n个节点和k条边的稀疏连通图，由n×n连接权矩阵{Aij}和n×1权重矩阵{Wi}表示。

1.4.1IEEE39节点系统模型

IEEE 39节点系统的算例，其拓扑模型为一个含有39个节点、46条边组成的稀疏连通图，分别见图1、图2、图3。

图1 部分连接权矩阵{Aij}

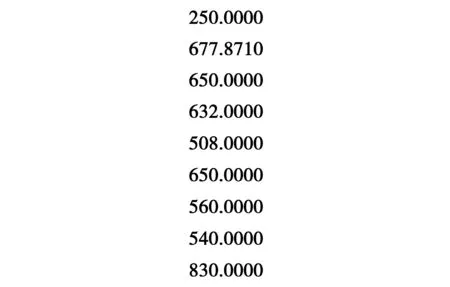
图2 权重矩阵{Wi}

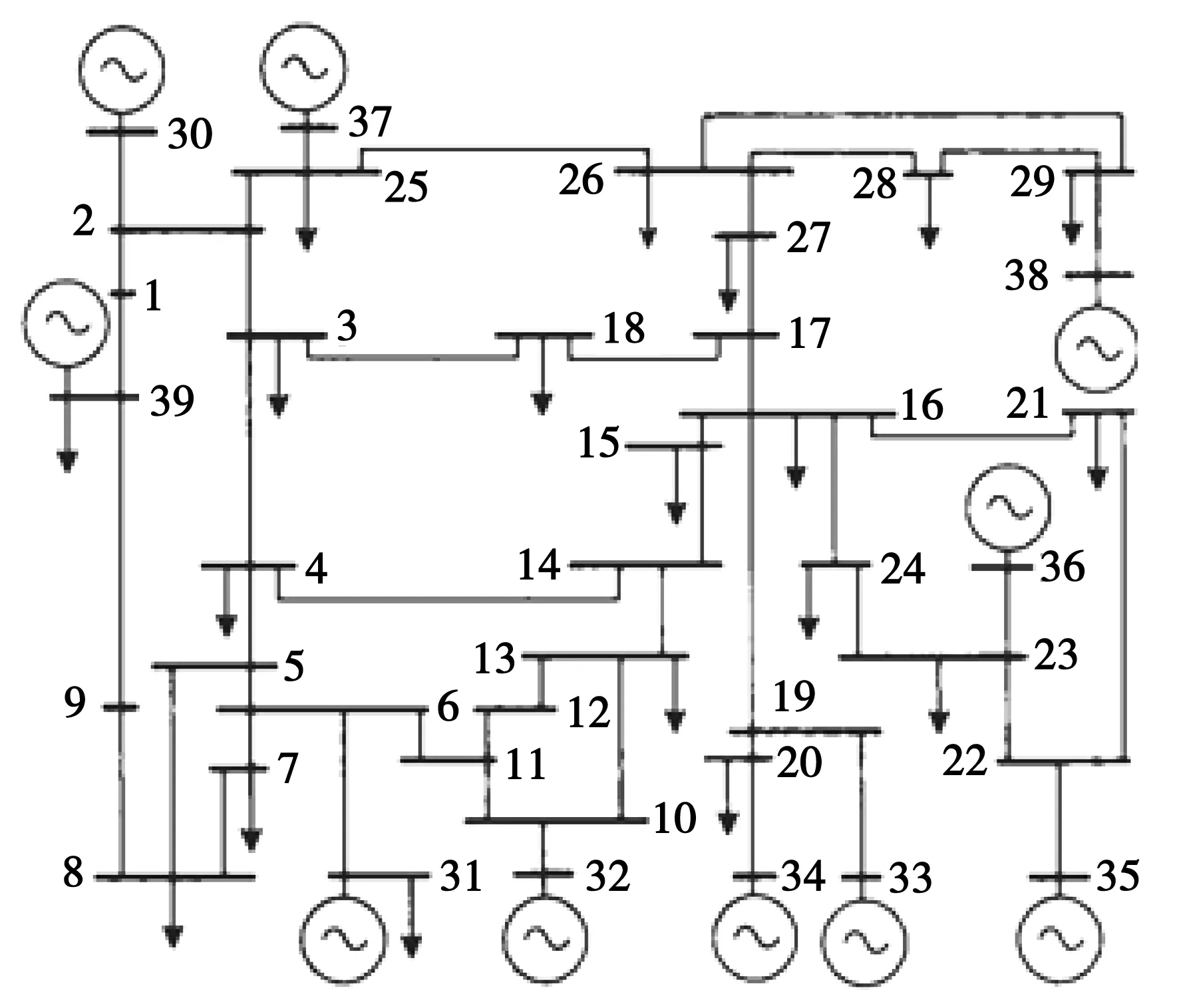
图3 IEEE 39节点系统接线

1.4.2 青海110kV某局部电网模型

对青海电网俄博图电厂和宁北电厂附近区域的110 kV电网进行建模和简化，建模原则同上，即得到一个由16个节点、14条边组成的稀疏连通图，由n×n连接权矩阵{Aij}和n×1权重矩阵{Wi}表示，分别见图4、图5、图6。

图4 部分连接权矩阵{Aij}

图5 权重矩阵{Wi}

图6 青海电网110 kV局部网架接线

1.5 脆弱线路辨识结果

1.5.1IEEE39节点系统辨识结果

本文采取带权重线路介数方法对IEEE 39节点系统进行脆弱线路辨别，这里引入潮流熵〔7〕方法，把带权重线路介数方法的排序结果与潮流熵方法的排序结果整合在一起形成对比，考虑筛选出的脆弱线路，表1即排名靠前的12条线路。

表1 IEEE 39节点系统脆弱线路比较

从表1可以看出，两个方法得出的脆弱线路大致上是相似的。如线路L16-17、线路L15-16、线路L21-22、线路L2-3、线路L1-2。这即可以证明本文提出的带权重线路介数方法能够完成电网脆弱线路的辨识。此外，分别采用两种识别方法所得到的关键线路也有所不同，主要原因是两种方法研究的方向不一样。

实际上，与电气介数方法〔8〕相比较，线路L16-17和线路L15-16都是排序结果所得到的脆弱线路，从传送能力上看，以上两条线路不具有优越性，但这两条线路都是能量传送的关键线路，如果发生故障会波及到整个区域的安全，电网运行会失稳甚至大规模停电。所以从位置上看是合理的。与功率介数方法〔5〕相比较，线路L21-22都为脆弱线路。线路L12-32、L2-30、L19-33、L21-22都处于发电机端口，而发电机作为功率传送的关键节点，对排序结果影响较大，这也表示该方法主要特点是从功率传送角度出发，但也具有局限性，结果并没有考虑的很全面。除此之外，通过功率介数法得出线路L12-32功率介数值最大，但是从拓扑结构上来看，该线路在电源出口段，然而除了本段线路，即使其发生故障，其余线路和发电机也很难有不可控的异常，不会导致严重甚至断电的风险。所以这样的结果不是很合理，功率介数方法也并不理想。

在带权重线路介数方法脆弱线路排序中，虽然线路L21-22处于系统边缘，但是承担的功率较重，所以排序靠前。而线路L14-15、L16-19、L17-27如果出现故障，发电机33-38则会停机，所以这些线路在带权重线路介数方法和电气介数方法中结果排序都靠前也是合理的。线路L2-3的拓扑位置极为重要，对于发电机30和37而言，该线路是它们功率传输的命脉，如果其发生故障，会使得30和37两台发电机受损，相连的所有线路的功率传送都会被影响，有可能发生功率转移，进而产生功率失衡的严重问题。而从继电保护原理来说，如果某些情况下线路L2-3保护没有动作，对于发电机30有比较大的影响，网络中的电压、电流、功率、功角也都会处于不稳定状态，由此可见，线路L2-3判断为脆弱线路也具有理论依据。

1.6.1 青海110kV某局部电网辨识结果

本文采取带权重线路介数方法对青海110 kV某局部电网进行脆弱线路辨别，把带权重线路介数方法的排序结果与线路暂稳校核的结果整合在一起形成对比，考虑筛选出的脆弱线路，表2即排名靠前的5条线路。

表2 青海110 kV某局部电网脆弱线路比较

从表2中可以看出，线路L1-2、线路L16-2、线路L13-12、线路L13-16、线路L5-13脆弱值较高，从线路暂稳校核结果上看，母线16或母线2发生单相瞬时性故障时，俄博图出现暂态失稳。水电厂切机作为常用的对付上述问题的一种有效手段，可以恢复电力系统的同步稳定性。此外，母线16供电等级更高，影响电网区域更大，如果发生故障会波及到整个区域的安全，电网运行会失稳甚至大规模停电。因此，通过介数值判断线路L16-2的脆弱程度具有可靠性。线路L13-16和线路L5-13作为环形接线的重要一环，输送负荷更大，脆弱值也相对较高。此外，线路L13-16作为110 kV厂站及330 kV厂站的联络线，脆弱值高也具有合理性。从拓扑结构上看，线路L1-2和线路L13-12作为电厂出线，都是能量传送的关键线路，一旦发现故障则会影响电厂功率送出，使得发电机受损，相连线路的功率传输也会被影响，所以脆弱值高也具有合理依据。

2 脆弱线路连锁攻击校验

2.1 线路连锁攻击模型

本文采用蓄意攻击和随机攻击两种模式来攻击网络：

1)蓄意攻击：线路按照介数大小排序，首先攻击介数值最高的线路，即将该线路断开，计算其网络效能函数；然后攻击剩余线路中介数值最高的线路并计算其网络效能函数，循环往复，得到一系列效能函数值，通过其变化可分析出蓄意攻击模式下的网络性能。

2)随机攻击：线路随机排序，首先攻击任意一条线路，即将该线路断开，计算其网络效能函数；然后攻击剩余线路中任意一条线路并计算其网络效能函数，循环往复，得到一系列效能函数值，通过其变化可分析出随机攻击模式下的网络性能。

2.2 网络效能评价模型

通过上述两种攻击模式对网络中线路进行攻击后，我们需要相应的指标去验证带权重线路介数方法辨识电网脆弱线路的合理有效性。在以往的研究中，网络效能函数、最大传输能力、连通域水平都是直接有效的模型。本文采用网络效能函数进行评估分析。

网络的有效效能定义为所有节点对间加权最短路径的长度的平均值，其表达式为：

(3)

其中：dij为节点对(i，j)间最短加权路径长度；N为网络的节点总数，V为节点集。

由此看出，网络效能函数是一个比值，以故障前效能与故障后效能做比。研究对象经过攻击崩溃后，网络效能都有一定程度的降低，降低的程度也反应出故障对系统的影响。因此本文运用这一指标具有可行性。

按照蓄意攻击和随机攻击两种模式对线路进行攻击，验证本文所提出的方法，具体流程框图如图7所示。

图7 脆弱线路连锁攻击校验流程图

2.3 脆弱线路连锁攻击校验结果

为验证带权重线路介数方法所得脆弱线路排序结果的合理性，本文釆用随机攻击和蓄意攻击两种攻击模式对IEEE 39节点系统和青海110 kV某局部电网分别进行攻击。通过分析不同攻击模式下网络效能函数的变化情况，来判断带权重线路介数方法是否合理有效，具体情况如图8和图9所示。

图8 IEEE 39节点系统两种攻击模式下网络效能的变化

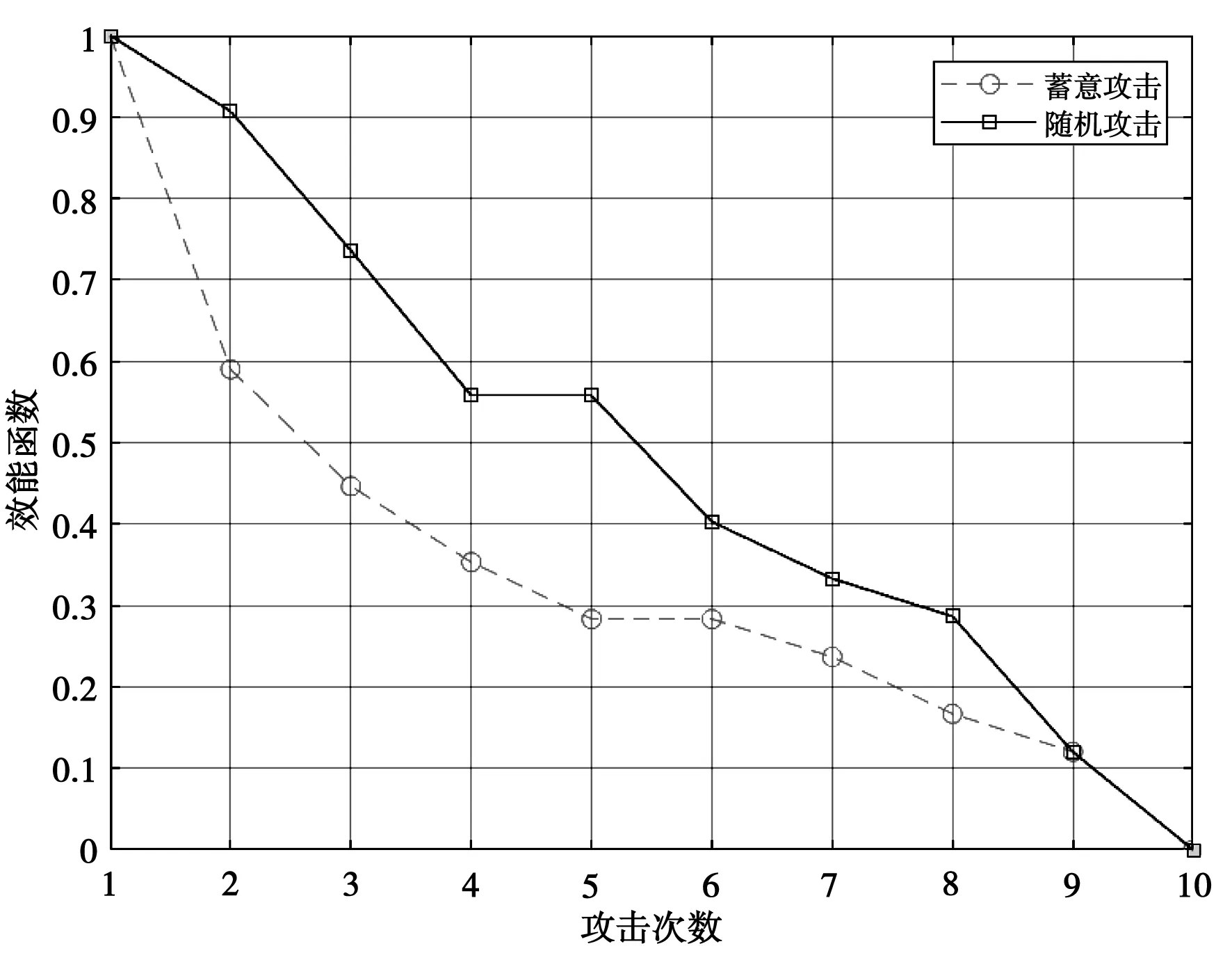
图9 青海110 kV某局部电网两种攻击模式下网络效能的变化

从模拟结果可以看出，线路一旦受到攻击，都将造成网络效能的下降。随机攻击网络线路时，网络效能呈缓慢线性关系下降，而蓄意攻击网络线路时，网络效能迅速下降，电网变得非常脆弱。与随机攻击相比，蓄意攻击下，网络效能下降得更明显和迅速。即带权重介数值大的线路对整个电力网络的连通性有着更重要的影响，也更为脆弱，进一步验证了带权重线路介数方法具有合理性和有效性。因此可以用带权重线路介数方法辨识电网的脆弱线路。

3 结论

本文以复杂网络理论为基础，针对线路引入了带权重线路介数指标，提出了基于带权重线路介数的电网脆弱线路辨识的方法。并以IEEE 39节点系统和青海110 kV某局部电网为算例，整理了带权重线路介数方法对脆弱线路辨识的排序结果，并与潮流熵法和暂稳校核结果作比较，得出本文所提的方法具有合理性。同时提出了对脆弱线路进行连锁攻击校验的思路，建立了网络效能函数模型，并引入了蓄意攻击和随机攻击两种连锁攻击模式，分析了不同攻击模式下网络效能的变化。蓄意攻击下，网络效能下降的更明显和迅速，即带权重介数值大的线路对整个电力网络的连通性有着更重要的影响，也更为脆弱。从而验证了本文提出的带权重线路介数方法具有有效性。