高压水条件下的水平单裂隙渗透系数取值探讨

李双双，黄 勇，周志芳

(河海大学地球科学与工程学院，江苏 南京 211100)

0 引 言

在研究高压水条件下裂隙岩体渗流特性的过程中，对裂隙岩体中水流形态的分析和判断非常关键。钱家忠等[1]认为高压水条件下的水流一般呈紊流形态，即非达西渗流，此时岩体渗透特性不再保持相对稳定，而出现复杂变化。特别是当岩体承受压力达到临界水力劈裂压力点时，岩体会发生劈裂，渗透性显著增大[2]。王化龙等[3]根据常规压水试验和高压压水试验的对比结果，阐明了在常规压水条件下裂隙岩体的渗透性要远低于在高压水条件下裂隙岩体的渗透性。有学者指出裂隙岩体在高压水条件下表现为在低压状态下渗透性较弱、在高压状态下渗透性较强[4-6]。在高压水条件下，如果仍采用层流理论计算渗透系数，则会导致裂隙岩体的渗透性存在较大的误差。因此，在高压压水试验过程中开展基于紊流状态下裂隙岩体参数取值研究显得非常必要。魏宁等[7]基于惠州抽水蓄能电站压水试验资料，通过数值模拟认为，裂隙岩体中的水流在高压条件下的运动与水流形态、岩体扩展情况、冲刷和堵塞现象中的一种或几种相关联。有学者基于渗流形态为非达西渗流，以压水试验中水压力、注入流量以及压水段长度等参数为基础，推导了高压水条件下的岩体渗透系数计算公式，阐明了水流状态的变化会对岩体渗透系数的取值造成重大影响[8-9]；基于高压压水试验过程的非线性渗流数学模型，讨论了非线性渗流数学模型中水头和流速随非线性参数的变化情况，且验证了数值解以及解析解的准确性[10-11]。在高压水作用下，裂隙岩体内的水压力会随裂隙长度的增加而呈指数型减小，随裂隙边缘宽度和张开速率的增大而增大[12]。裂隙岩体的渗透系数的取值不仅受岩体性质的影响，也和水压力的大小和变化相关联[13]。因此，采用压水试验孔内水压力参数计算渗透系数还有待商榷。

本文针对某抽水蓄能电站在高压压水试验过程中出现的异常现象，基于水平单裂隙模型，定量确定高压压水试验下裂隙岩体渗透系数随压入流量的变化关系，并与常规压水试验公式计算出渗透系数进行比较，探讨在高压压水试验过程中，运用常规压水试验公式计算渗透系数的适用性，为水利水电工程的渗流分析和防渗参数取值提供理论依据。

1 高压水条件下渗透系数公式推导

1.1 常规压水试验条件下渗透系数的确定

基于SL 31—2003《水利水电工程钻孔压水试验规程》开展常规压水试验，最大压力不超过1 MPa，此时岩体一般不会发生渗透破坏，裂隙岩体中的水流可近似为层流，满足达西定律，岩体的渗透系数K可表示为[14]

(1)

式中，Q为最大压力阶段对应流量值；P为最大压力阶段水压力值，以水柱高度表示；L为压水段长度；rw为压水孔半径。一般压水孔半径取值为75 mm，压水段长度取值为5 m，因L/(2rw)远大于1，则式(1)可以化简为

(2)

1.2 高压水试验条件下渗透系数的确定

对于大型的深埋地下工程，为获取岩体的完整性和渗透性等指标，通常需要进行高压压水试验。在高压水条件下，裂隙岩体中的水流形态常常呈现为紊流(非达西渗流)，其水流运动特征可以表示为[15]

(3)

式中，Pf为裂隙岩体中的流体压力；kf为裂隙岩体的渗透率；μ为流体的动力粘滞系数；v为裂隙岩体中流体流速；ρ为流体的密度；β为非达西流参数。由于在压水试验过程中，岩体的平均渗透特性是主要考虑因素，所以不考虑渗透系数张量。因此，对于一维径向流，在进行岩体渗透系数推导时，式(3)可以改写为

(4)

1912年，克拉斯诺波里斯基基于水流在紊流状态下，提出了渗流速度v、渗透系数K和水力梯度Jf之间的关系[8]

(5)

且有

(6)

式中，H为水头；r为径向半径；g为重力加速度。将式(6)和式(5)代入式(4)中，则式(4)变为

(7)

式中，负号代表水力梯度方向与水流速度方向相反，即

(8)

两边同时平方并整理得

(9)

将dr移至式(9)的右端，两边同时积分得

(10)

式中，P1、P2为裂隙两端压力值。令ΔP=P1-P2，则上述积分可表示为

(11)

由于在高压压水试验条件下，裂隙岩体内的水压力变化相当复杂，研究裂隙岩体内的水压力随径向半径的变化规律较困难。由于单裂隙是研究裂隙岩体渗流特性的基础[16]，则基于平行板裂隙模型(见图1，图1中δ为隙宽；l为平行板长度，Q为流量)，陈轶杰等[17]给出了在紊流状态下的平行板裂隙流量Q的解析式

图1 高压压水试验水平单裂隙模型示意

(12)

式中，ε为流体运动粘滞系数；ρ为流体密度。

根据平行板裂隙模型，考虑裂隙处于饱水状态，得到l=r，将式(11)代入式(12)中，得

Q=-127.79ε+

(13)

(14)

将式(14)代入式(13)中，得

(15)

光滑平行板裂隙中，水流呈紊流运动时的单宽流量q可表示为[18]

(16)

根据式(5)和式(16)，则K与δ之间的关系可以表示为

(17)

将式(17)代入式(15)中，得到Q和K的关系

(18)

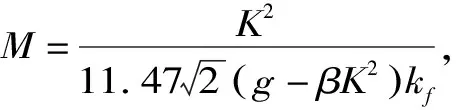
(19)

为了简化计算，本文通过拟合方法对式(19)进行简化，假定M的取值范围为1～140 m-1，将表1中的参数取值代入式(19)，计算得到流量Q。

表1 参数取值

为了后文实例分析，其中kf取值为黑麋峰抽水蓄能电站经验值，对于其他电站的kf值可根据实际值进行更改。由于流量Q为正值，所以本文截取了流量为正值的阶段进行分析。根据计算结果，此时流量Q的取值范围为0～100 L/min，满足绝大部分高压压水试验。通过拟合曲线可得到Q和M的关系为

M=-0.001 8Q2+1.333 6Q+16.913

(20)

推导可得，渗透系数K和压入流量Q的关系为

(21)

式(21)显示，当Q<260 L/min时(绝大多数现场高压压水试验满足)，渗透系数K随着流量的增加而增大，且K与Q为非线性关系。根据式(21)，取不同的Q值，可以得到不同的K值。渗透系数K和压入流量Q关系见图2。从图2可以看出，当流量Q<10 L/min时，K与Q的非线性关系不明显，且近似为线性关系；当超过该点值时，K与Q的关系开始呈现明显的非线性。因此，对于高压压水试验，根据不同的压入流量，采用式(21)可以计算不同试验阶段的裂隙岩体渗透系数。

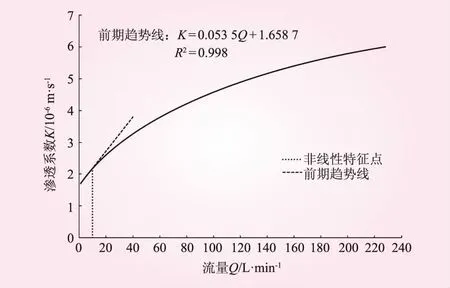
图2 渗透系数与压入流量的关系

2 工程实例分析

本文应用黑麋峰抽水蓄能电站的高压压水试验资料来验证式(21)的合理性。该电站地处于湖南省长沙市境内，电站上、下水库正常蓄水位分别为400 m和103.7 m，发电额定水头为295 m，额定流量为118 m3/s，总装机容量为1 200 MW。其中，F15断层位于高压岔管区，断层产状为N10°～30°E，SE∠80°～85°，破碎带最大宽度4 m，充填花岗伟晶岩脉、花岗碎裂岩、石英脉和断层泥等，胶结一般，具有一定的导水性。为了了解在高压水作用下断层的渗透性和渗透稳定性，黑麋峰抽水蓄能电站在①引水隧洞下平段打了1个高压压水试验孔，揭露并穿过F15断层。试验孔剖面见图3[19]。

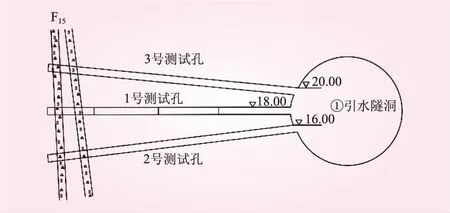
图3 1号试验孔剖面(高程：m)

对1号试验孔进行高压压水试验，压水过程采用自动控压系统进行压水，并每隔1 min记录1次压水压力值和流量值。图4为1号试验孔断层段的压力与流量关系曲线，曲线明显分成3个阶段：第1阶段压力P<4 MPa，流量Q=1～2 L/min，岩体透水性较低。第2阶段压力P=4～6 MPa，流量Q=2～10 MPa，流量增大，岩体透水性呈增长趋势。第3阶段压力P>6 MPa，流量发生突变，岩体透水性显著增强。根据压力与流量关系曲线，可以得出断层段的水力劈裂压力约为4.1 MPa。本研究将F15断层当做平行板模型考虑，并采用式(21)计算其渗透性。同时，也采用Hvorsle公式计算断层的渗透系数。

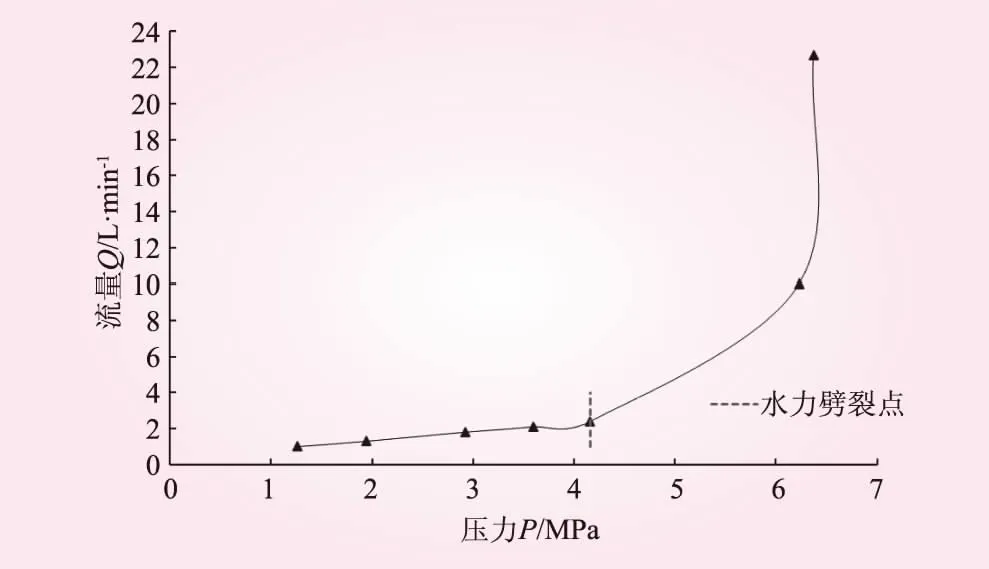
图4 1号试验孔压力与流量的关系

基于Hvorsle公式计算的渗透系数K与流量Q的关系见图5。从图5可知，水力劈裂前，随着流量Q的增加，渗透系数K在逐渐降低。可能是因为随着试验水压力升高，岩体压入水量也随之加大，但其增量却小于水压力的增量，即采用式(2)计算的渗透系数偏小，甚至出现“岩体高压透水性指标低(好)于常压”的反常现象，而实际上在高压压水条件下裂隙岩体的透水能力是比较大的。因此，在高压条件下，采用常规压水试验公式计算渗透系数存在较大误差，表明在高压水条条件下，不适宜采用常规压水试验公式计算渗透系数。水力劈裂后，岩体的渗透性显著增加。

图5 基于Hvorsle公式计算的渗透系数与流量的关系

基于推导公式计算的渗透系数K与流量Q的关系见图6。从图6可知，在发生水力劈裂前，随着流量Q的增加，计算的渗透系数值在逐渐增大，与实际的高压压水试验结果较吻合。前期由于Q的变化量较小，K与Q的非线性关系不明显，当达到Q>10 L/min后，K与Q的关系逐渐呈现非线性，这与推导得到的理论曲线图2相符合。说明在高压压水条件下，随着Q的逐渐增大，特别是大于10 L/min时，K与Q的非线性关系比较明显。

图6 基于推导公式计算的渗透系数与流量的关系

黑麋峰电站钻孔试验资料显示，高压岔管区断层破碎带及其影响破碎带透水率一般介于1～6 Lu之间，局部小于1 Lu，大于3 Lu试段数占总试段数的50%，为弱～微透水介质。因此，就断层破碎带而言，其渗透系数应大于i×10-5cm/s。本文分别使用Hvorsle公式和推导公式计算了断层破碎带的渗透系数，并与按透水率换算公式[20]计算出的渗透系数进行对比。Hvorsle公式和使用按透水率换算公式所得到的渗透系数比较接近，约为0.7×10-6～7.0×10-6cm/s，但对于断层破碎带而言，这2种方法计算得到的渗透系数显然偏小，而推导公式所得到的渗透系数约在1.67×10-4～2.72×10-4cm/s，与实际比较吻合。

不同方法计算的渗透系数值比较见表2。从表2可知，推导公式所得到的渗透系数明显大于其他2种方法所得到的渗透系数值，大约为Hvorsle公式得到的K值的57～257倍(1～2个数量级)，为按透水率换算公式得到的K值的38～156倍，说明在高压水条件下，Hvorsle公式或按透水率换算公式计算渗透系数，可能与实际渗透系数差别较大。

表2 不同方法计算的渗透系数值比较

3 结 语

本文针对高压压水试验工程中使用Hvorsle公式计算渗透系数时出现的异常现象，提出了一种水平单裂隙模型，推导了高压压水试验下裂隙岩体渗透系数随压入流量的变化关系，得出以下结论：

(1)当压入流量较小时，渗透系数与压入流量近似呈线性关系；随着压入流量增大(>10 L/min)，两者的非线性关系比较明显。

(2)采用推导公式所得到的渗透系数明显大于其他2种方法所得到的渗透系数值，大约为使用Hvorsle公式得到的K值的 57～257倍，为按透水率换算公式得到的K值的38～156倍，相差都在1～2个数量级。与断层带实际渗透系数较吻合。

(3)在高压水条件下，不适用采用Hvorsle公式或按透水率换算公式计算渗透系数，可以采用本文推导公式计算。