用哲学原理解决化工原理流体流动定性问题

唐正姣，陈苏芳，李萍，覃远航，汪铁林

武汉工程大学化工与制药学院，武汉 430205

教育部2020年5月28日印发《高等学校课程思政建设指导纲要》的通知要求：理学、工学类专业课程，要在课程教学中把马克思主义立场观点方法的教育与科学精神的培养结合起来，提高学生正确认识问题、分析问题和解决问题的能力。习近平指出：“我们党自成立起就高度重视在思想上建党，其中十分重要的一条就是坚持用马克思主义哲学教育和武装全党。学哲学、用哲学，是我们党的一个好传统[1]。”化工原理课程蕴含丰富的哲学元素，提炼出的哲学元素主要有[2-6]：“运动的绝对性和静止的相对性、解决问题抓主要矛盾、量变到质变、对立统一规律、透过现象看本质等。”上述文献都是从哲学在化工原理中的映射角度进行教学即课程内容体现了某种哲学思想。鲜见用哲学原理解决工程问题的教学探讨文献报道。化工原理中管路定性分析问题是应用化工原理理论解决工程实际问题的重要体现之一，同时也是学生学习的难点之一。学生运用流体流动的守恒原理可以进行定性问题的分析，但分析过程相对繁琐，学生理解起来常常觉得困难。笔者尝试运用哲学原理进行管路定性分析问题的教学实践，学生学习后反映比用流体流动的守恒原理解决类似问题简单，并且容易掌握。

1 用动与静的辩证关系分析简单管路的流量与压强变化

例1[7]对于图1所示简单管路，设各段管径相同，高位槽内液面恒定，流体作定态流动。阀门由全开转为半开时流量、阀前压力、阀后压力如何变化？

图1 例1附图

分析：对于一定的管路系统，流量属于动，取决于阀门开度变化；静压强则属于静，取决于流体积累量的变化。以截面A与截面B包含的范围作为控制体，阀门上游压强pA(静)、管路流量qV(动)阀门下游压强pB(静)这三个物理量相互影响。从pA到qV，从qV到pB反映了静转化动、动转化静两个过程即静→动→静。在分析过程参数变化时以明显变化的参数作为分析问题的突破口。当阀门开度变小，流动通道变窄，变化空间减小，流量减小。从流动过程分析，动由静转化而来，阀门开度变小即动态量变小则上游被转化的静态量减小，从而积累量增加即上游压强增大；下游的静态量来自于上游的动态量的转化，上游动态量减小，则能转化的动态量减小即下游的静态量减小(静压强下降)。按照动静相互转化的规律可以表述为：阀门开度减小，通过阀门的动态量减小，上游积累量增加，下游积累量减小。即阀门开度减小，流量减小，阀门上游静压强上升，下游静压强下降。根据流体流动的守恒原理进行管路分析得到以下结论[7]：其他条件不变时，任何局部阻力的增加，将使管内的流量下降，使上游压强上升，使下游压强下降。可见根据流动过程动与静的辩证关系分析得到的结论与根据流体流动的守恒原理推导的结论一致。

2 矛盾论在阻力损失定性分析中的应用

例2[8]如图2所示，敞口容器液面保持不变，阀门A和B的阻力系数分别为ζA和ζB，h1和h2为连接管路的玻璃管显示的液面高度，若ζA不变，ζB增大，h1、h2、h1-h2如何变化？

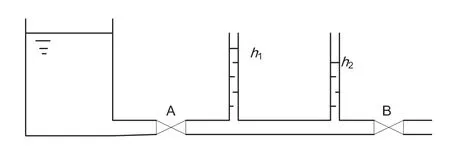
图2 例2附图

分析：黄婕等[8]分析时指出：ζA不变，ζB增大，表明阀门B关小，则流速u减小，B处阻力增大，h1、h2位置处于阀门B的上游，其数值反映上游的压强，所以h1、h2增大；因为u减小，所以AB直管段的阻力损失减小，(h1-h2)减小。从上面的分析可知，对于直管阻力，管长l、直径d不变时，u减小，阻力减小；对于局部阻力，阻力系数增大，阻力增大。这个结论是分析流体管路阻力损失问题分析的基础。那么为什么有这样的结论？根据范宁公式阻力损失hf=λlu2/(2d)，u变大，雷诺准数Re(=duρ/μ)变大摩擦系数λ变小，所以无法判断hf的变化；对于局部阻力，hf=ζu2/2，阀门开度变小，局部阻力系数ζ增大，流速u变小，也无法判断hf的变化。何潮洪等[9]指出：对于直管阻力，摩擦系数λ变化不大，可视为常数。而对于局部阻力为什么阀门开度变小，局部阻力变大则未见教材给出解释。诚然可以让学生直接记住结论但缺乏说服力。笔者应用辩证法进行分析：直管阻力中的u与λ互为矛盾，u是矛盾的主要方面，所以根据重点论，直管阻力损失随u变化而变化。局部阻力中的ζ与u互为矛盾，ζ是矛盾的主要方面，所以根据重点论，判断局部阻力损失随ζ变化而变化。

3 用整体与局部的辩证关系分析复杂管路的流量变化

例3[7]流体从高位槽流出经总管分流至两支管，阀门全开时各支管的流动参数如图3所示；若将支管2的阀门A关小，支管2、支管3、总管的流量如何变化？

图3 例3附图

分析：支管管路2和支管3为可以看成事物的局部，总管可以看成事物的全局。毛泽东在总结战争经验时，具体地分析了全局与局部的辩证关系。毛泽东指出：“全局是由它的一切局部构成的。若组成战争全局的多数战役失败了，或有决定意义的某一两个战役失败了，全局就立即起变化。这里说的多数战役和某一二个战役，就都是决定性的东西了[10]。”因此对全局有决定性影响的局部，关系能否实现全局性的目标。对于分支管路，有阀门开度变化的支管就是支管中起决定作用的管路。所以总管流量变化趋势与有阀门开度变化的支管的流量变化趋势一致。另外从矛盾论分析，与之平行的其他支管与有阀门开度变化的支管互为矛盾，所以其他支管的流量会下降。根据流体流动的守恒原理得到[7]：阀门A所在支管流量下降，与之平行的支管流量上升，总管流量下降。可见根据流动过程的全局与局部的辩证关系结合矛盾论分析得到的结论与根据流体流动的守恒原理推导的结论一致。

例4[8]如图4所示的输水系统中，阀门A、B和C半开时，各管路的流速分别为uA、uB、uC。现将B阀关小，则各管路流速如何变化？

图4 例题4附图

分析：在A、B支管中，B阀所在支管起决定作用，B阀开度减小，则uB减小；总管流速与支管B的流速变化一致，即uC减小，与之平行的支管A的流速与支管B的流速互为矛盾，uB减小，故流速uA增大。这与黄婕等[8]利用流体流动的守恒原理分析的结论一致。

4 综合应用举例

例5[11]如图5所示，用离心泵将贮水池中的水经总管及A、B两支管送至敞口槽中。贮水池与敞口槽水面高度差可不计。现将阀门kA关小，其他条件不变，试分析总管、A、B支管流量、压力表读数pO、pM的变化情况。

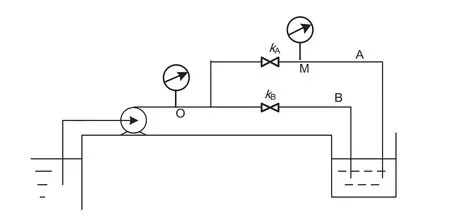
图5 例题5附图

分析：将阀门kA关小，A支管为起决定作用的支管，A支管流量下降；总管流量与A支管流量变化趋势一致即总管流量减小；B支管与A支管互为矛盾，A支管流量下降，则B支管流量增大；压力表读数pM在阀门kA的下游、pO在阀门kA上游，根据动与静的辩证关系得到阀门kA关小，pM读数减小，pO读数增大。这与文献[11]的分析结果一致。

例6[12]如图6所示管路，若两敞口容器内液位恒定，试问：(1) A阀开大，流量qV、压力表读数p1、p2、支管阻力损失比hf1/hf2、支管流量比qV1/qV2如何变化？(2) B阀关小，流量qV、压力表读数p1、p2、支管阻力损失比hf1/hf2、支管流量比qV1/qV2如何变化？

图6 例题6附图

分析：(1) 阀门A开大，通量增大，qV增大；阀的上游积累量减小即压力表读数p1减小；阀门的下游积累量增加即压力表读数p2增加；hf1/hf2为并联的支管阻力比为1；作为局部的支管的阀门开度不变，整体变化，局部跟随变化qV1/qV2不变。(2) 阀门B关小，起决定作用的局部即支管B的流量变小，局部影响整体qV减小；阀门B关小，阀门B的上游积累量增加，压力表读数p1、p2都增加；hf1/hf2为并联的支管阻力比为1；阀门B关小，阀门C所在支管与阀门B所在支管互为矛盾，qV1变小，qV2变大，qV1/qV2变小。这与文献[12]的结果一致。

5 教学实践与学生反馈

笔者在2018级化工原理提高学习班开展了用哲学原理解决化工原理流体流动定性问题的教学实践，并通过问卷网进行问卷调查。

问题1：用哲学原理解决流体流动定性问题的教学方法，你觉得怎样？设置了四个选项：A. 非常好，B. 好，C. 一般，D. 不好。

问题2：你学习用哲学原理分析流体流动的定性问题后，对于你来说，用哲学原理分析的准确度高还是用化工原理的知识分析的准确度高？设置了三个选项：A. 哲学原理，B. 化工原理，C. 都一样。

问题1、问题2的问卷结果分别见图7、图8。

图7 用哲学原理解决流体流动定性问题教学方法评价问卷结果图

图8 用哲学原理与化工原理的知识进行定性分析的准确度问卷结果图

问题3：请你对用哲学原理解决流体流动定性问题做出简单评价？学生反馈总结如下：(1) 教学形式变新颖，学生写道：“哲学的加入使课堂生动起来了，有利于我们对知识点的理解，教课形式变得新颖了。”(2) 提升学习兴趣，学生写道：“让我对化工原理以及哲学方面的内容产生了浓厚的兴趣，也给我在化工原理的学习过程中指了一条明路。”(3) 提升解题速度，学生写道：“哲学原理解决流体流动性问题，个人觉得会让复杂化的问题简单化，有助于我们理解，可以让一些抽象化的概念，通过哲学原理，更加贴近生活，从而快速解决问题；让做题过程判断更加简化快速，在学习的过程中运用效果很好，在某些问题上解决速度更快；动静结合起来十分方便；很方便也很准确，节约了许多时间，大大提高做题速度和效率，尤其是非常适用于选择题；非常合适，可以与化工原理相结合更好地解答问题。”(4) 提升运用哲学原理解决问题的能力，学生写道：“挺好的，一边想不通，换个角度豁然开朗；哲学原理能在一定程度上帮助理解化工原理的问题可以转换思维，从不同角度看问题；提供了另外一种解决问题的思路，当用化工原理知识难以解决问题的时候，可以采用哲学原理去思考。同时也可以利用哲学原理去检验化工原理内容判断的准确性。二者有一种相辅相成的作用。”也有个别同学认为哲学就没学好，所以对于他们来说，作用甚小。

综合问卷结果可见，绝大多数学生对于用哲学原理解决流体流动定性问题持肯定、欢迎的态度。

6 结语

马克思主义哲学是科学的世界观、方法论和价值观，是人类智慧的结晶。对于流体流动过程的定性分析问题，采用哲学原理进行分析判断比直接应用专业知识解决更容易理解、解题速度更快。教学实践表明，大部分学生对用哲学原理解决化工原理的定性问题学习兴趣浓厚，打破了学生固有的用专业知识解决专业问题的思维定势，培养与提高了学生用哲学原理解决实际问题的能力。这是哲学与化工原理相结合的生动实践，也响应了教育部要求在课程教学中把马克思主义立场观点方法的教育与科学精神的培养结合的指导方针。笔者将继续探索在其他单元操作中用哲学思想解决专业问题的教学。