Undecidability Results of Modal Definability in Extended Modal Languages*

Zhiguang Zhao

Abstract. In the present paper,we apply the methodology in Balbiani and Tinchev(2016)to show that for the modal language with universal modality LU,tense language LT,hybrid languages LH, LH(@),Chagrova’s theorem holds that the modal/tense/hybrid definability of first-order sentences with respect to certain classes of frames is undecidable,by using similar techniques as stable classes of Kripke frames.

1 Introduction

In the model theory of modal logic,the modal definability problem of first-order formulas can be stated as follows:given a first-order formulaα,for the class of Kripke frames it defines,whether there is a modal formulaφthat defines the same class of Kripke frames.The celebrated Goldblatt-Thomason Theorem([16])states that given an elementary class of Kripke frames,it is modally definable if and only if it is closed under taking disjoint unions,generated subframes and bounded morphic images and reflects ultrafilter extensions.However,this theorem does not provide an algorithm to check if a given first-order formula is modally definable.As is shown by Chagrova in[10],this problem is undecidable.1For further similar results,see[7,9,11]and[8,Chapter 17].

The problem of modal definability is further studied in[1-4,12-15].In[2],it is shown that modal definability for the class of all partitions is PSPACE-complete.In [3],it is further shown that modal definability in the modal language extended with universal modality for the class of all partitions is PSPACE-complete.In [12,14],it is shown that for the modal language and the modal language with universal modality,the modal definability problem for the class of KD45-frames is PSPACEcomplete.In[4],by applying the stable class technique,it is shown that with respect to certain frame classes,the modal definability problem of first-order sentences is undecidable,which is also an alternative proof of Chagrova’s result.In[1],by using similar techniques,it is shown that with respect to the class of all Euclidean frames,the modal definability problem is undecidable.The basic idea of the stable class technique can be described as follows:Given a class C of Kripke frames,by showing that the class C is stable,the problem of checking whether a first-order sentenceαis valid in C (C-validity problem) can be reduced to the modal definability problem ofαin C(C-modal definability problem).Therefore,if the first-order theory of C is undecidable,then the modal definability of first-order sentences in C is undecidable.In the present paper,what we are going to investigate is to what extent can we apply the same technique to get similar undecidability results,if we extend the modal language by adding converse modality,nominals,the@-operator,universal modality,etc.Indeed,in the proof that C-validity problem can be reduced to C-modal definability problem,the only parts that uses properties of the modal language are the following:(a).the modal language contains a formula like⊥such that it is valid on no Kripke frames in C;(b).the relation FF′that F′validates more(or the same)modal formulas than F.If we revise the definition of therelation by replacing modal formulas by tense/hybrid/…formulas,then we can get similar notions of stability in the extended modal languages,without changing the proof of the reducibility mentioned above.Therefore,once we have revised the definitions of stability according to the extended modal language,we can use the same technique to construct the witnesses of stability.What one needs to take care is that by adding expressivity to the modal language,the validity of extended modal formulas are preserved under less kinds of frame constructions,e.g.for tense logic,the notion of p-morphic image should be revised accordingly,and for the language with universal modality,the validity is not preserved under taking disjoint union or generated subframe anymore.Therefore,we need to take care of choosing appropriate frame F′to make sure that FF′holds for the extended modal languageLin consideration.

The structure of the paper is as follows:Section 2 presents preliminaries on the extended modal languages and first-order language concerned in the paper.Section 3 sketches the stable class methodology as well as giving new undecidability results for the class of serial frames in the basic modal language.Section 4 gives the proofs thatLU-,LT-,LH-andLH(@)-definability for certain classes of Kripke frames are undecidable.Section 5 gives conclusions and further directions of research.

2 Preliminaries

In this section,we collect preliminary definitions and propositions for modal logic,tense logic and hybrid logic.For more details,see[4-6].

2.1 Extended modal languages

SyntaxGiven a set of propositional variables Prop,a set of nominals Nom,the syntax for modal logicLM,modal logic with universal modalityLU,tense logicLT,hybrid logicLH,hybrid logic with@-operatorLH(@)(we call these languages(extended)modal languages)are defined as follows:

wherep ∈Prop.

LUis obtained by adding the clausesUφandEφtoLM;

LTis obtained by adding the clauses ■φand ◆φtoLM;

LHis obtained by adding the clauseitoLMwherei∈Nom;

LH(@)is obtained by adding the clause@iφtoLH.

SemanticsGiven the(extended) modal languages,they are interpreted on Kripke frames F=(W,R) whereW ／=∅,R ⊆W × W.A Kripke model is a tuple M=(W,R,V)where(W,R)is a Kripke frame andV:Prop∪Nom→P(W)is an assignment such thatV(i)is a singleton for all nominalsi∈Nom.

Given a Kripke model M=(W,R,V),the satisfaction relation is defined as follows:

A formulaφis true in a model M(notation:M ⊩φ),if M ⊩φfor allv ∈W.φis valid in a frame F(notation:F ⊩φ),ifφis true in all models based on F.φis valid in a frame class C(notation:C ⊩φ),ifφis valid in all frames in C.A frame F isL-weaker than a frame F′(notation FF′),if for allL-formulasφ,if F ⊩φthen F′⊩φ.

2.2 Frame constructions and validity preservation

In the stable class techniques,therelation is an important technical tool,and it can be shown by proving that certain frame constructions preserveL-validity.Notice that here we only talk about frame constructions rather than model constructions,we do not need to revise the definitions of the frame constructions for hybrid logic.

Definition 1(Generated subframe).Given two Kripke frames F=(W,R) and F′=(W′,R′),we say that F′is a generated subframe of F ifW′ ⊆W,R′=R ∩(W′×W′),and for allw ∈W′andv ∈Wsuch thatRwv,we havev ∈W′.

Definition 2(Disjoint union).Given Kripke frames Fi=(Wi,Ri) (i ∈I) with disjoint domains,their disjoint union ⊎

iFi=(W,R)is defined asW:=∪

i∈I Wi,R:=∪

i∈I Ri.

Definition 3(Bounded morphic image).Given two Kripke frames F=(W,R)and F′=(W′,R′),we say that F′is a bounded morphic image of F if there is a surjective mapf:W →W′such that the following conditions hold:

· for allw,v ∈W,ifRwvthenR′f(w)f(v);

· for allw ∈W,v′ ∈W′,ifR′f(w)v′then there exists av ∈Wsuch thatRwvandf(v)=v′.

Definition 4(Tense generated subframe).Given two Kripke frames F=(W,R)and F′=(W′,R′),we say that F′is a tense generated subframe of F if

·W′ ⊆W;

·R′=R ∩(W′×W′);

· for allw ∈W′andv ∈Wsuch thatRwv,we havev ∈W′;

· for allw ∈W′andv ∈Wsuch thatRvw,we havev ∈W′.

Definition 5(Tense bounded morphic image).Given two Kripke frames F=(W,R)and F′=(W′,R′),we say that F′is a tense bounded morphic image of F if there is a surjective mapf:W →W′such that the following conditions hold:

· for allw,v ∈W,ifRwvthenR′f(w)f(v);

· for allw ∈W,v′ ∈W′,ifR′f(w)v′then there exists av ∈Wsuch thatRwvandf(v)=v′;

· for allw ∈W,v′ ∈W′,ifR′v′f(w)then there exists av ∈Wsuch thatRvwandf(v)=v′.

It is easy to see that the modal languageLMis preserved under taking the first three kinds of frame constructions defined above:

Proposition 1.

·Given two Kripke framesFandF′,ifF′is a generated subframe ofF,then for any LM-formula φ,ifF ⊩φ,thenF′⊩φ(i.e.,FF′);

·Given a class of frames{Fi | i ∈I},for any LM-formula φ,ifFi⊩φ for alli ∈I,then

·Given two Kripke framesFandF′,ifF′is a bounded morphic image ofF,then for any LM-formula φ,ifF ⊩φ,thenF′⊩φ(i.e.,FF′).

We can obtain similar results for extended modal languages:

Proposition 2.

·For the modal language with universal modality LU,its validity is preserved under taking bounded morphic images;

·For the tense logic language LT,its validity is preserved under taking tense generated subframes,disjoint unions and tense bounded morphic images;

·For the hybrid logic languages LH and LH(@),their validities are preserved under taking generated subframes.

2.3 First-order language

In this subsection we give the necessary notations and definitions in first-order logic and relativization.We follow the presentations in[4].

SyntaxGiven a set of individual variables Var,the first-order languageL1is defined as follows:

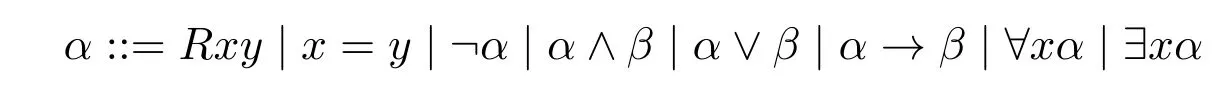
TruthGiven a frame F=(W,R),the satisfaction relation between first-order formulaα() and F with respect to a listsof worlds in F (notation:is defined as follows:

RelativizationThe relativizationof a first-order formulaγwith respect to another first-order formulaαand an individual variablexis defined as follows:

whereα[x/y] is obtained by replacing all free occurrence ofxinαbyy.When writingwe assume that individual variables occurring inαandγare disjoint.

For relativization and relativized reducts,we have the following theorem:

3 Undecidability of Modal Definability:The Stable Class Technique

In this section,we recall the technique used in [4] to show the undecidability of modal definability of first-order sentences.The basic idea is to use the so-called stable class of frames.Balbiani and Tinchev ([4]) showed that if a class of framesis stable,then the validity problem of first-order sentences in C is reducible to the modal definability problem with respect toOnce the validity problem of firstorder sentences inis undecidable,the modal definability problem with respect tois undecidable.

3.1 The stable class technique

Now we give the relevant definitions in[4].

Definition 7(Modal definability).Given a class of frames,a first-order sentenceαis modally definable with respect to C if there is a modal formulaφsuch that for all frames F∈,F ⊨αiff F ⊩φ.

For other extended modal languages,the definition is similar.

Definition 8(Stable class).A class of framesis stable if there is a first-order formulaand a first-order sentenceβsuch that the following two conditions hold(we say thatis a witness of the stability of):

The definition above is defined for the language of modal logic,and it can be adapted to other extended modal languages by revising the index of

Now we briefly recall the proof of Balbiani and Tinchev’s reduction theorem:

Theorem 4(Theorem 1 in [4]).If a class of framesis stable,then the validity problem of first-order sentences inis reducible to the modal definability problem with respect to

Proof.See[4,Theorem 1].Here we repeat it for the sake of checking the details of the proof.

It is easy to see that the only two places that uses the properties of the modal language are the following:

· The modal language contains a formula like⊥such that it is valid on no Kripke frames in C;

· The relation FF′that F′validates more (or the same) modal formulas than F.

Therefore,when considering an extended modal languageL,once it contains⊥and we consider the relation FF′instead of FF′when defining the stable class and proving the theorem,we can obtain the definition ofL-stable class by replacing FF′with FF′,and obtain the analogue of the theorem above by the following theorem:

Theorem 5.If a class of framesis L-stable,then the validity problem of first-order sentences inis reducible to the L-definability problem with respect toC.

3.2 Example of showing undecidability of modal definability within certain frame class

We can give the following example that modal definability problem is undecidable in the class of serial frames,i.e.the frames satisfying∀x∃yRxy,by showing that the class of serial frames is stable.To the author’s knowledge,this result is original.

Theorem 6.The classSer of serial frames is stable.Therefore,the modal definability problem inSer is undecidable.

Proof.For the validity problem ofTh(Ser),since the first-order theory of lattice is a finite extension ofTh(Ser),the undecidability ofTh(Ser) follows from the undecidability of the first-order theory of lattice[17].Therefore,it suffices to show thatSeris stable.

Now defineα(x):=∃yRyx,β:=¬∀xRxx,then we can show that conditions 1 and 2 hold forSerwitnessed by(α(x),β):

· For condition 1,take any frame F=(W,R)∈Ser,F is serial.Consider a frame F′=(W′,R′)which is the relativized reduct of F with respect toα(x),then it is easy to see thatW′ ／=∅,since for a serial frame F=(W,R),R／=∅,so there exists aw ∈Wsuch thatwhas anR-predecessor.We can show thatR′is a serial relation onW′:suppose otherwise,whasR-successors but noR′-successors,then the worlds in the setR[w]={v ∈W | Rwv}are all deleted when taking the relativized reduct,so thosevs have noR-predecessor,a contradiction toRwv.

· For condition 2,for any serial frame F0=(W0,R0)∈CSer,we can construct F and F′as follows:

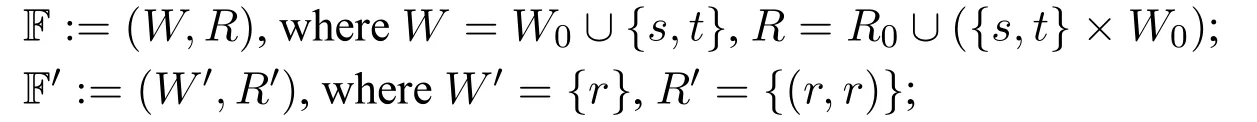
It is easy to see that F and F′are serial.Since in F,the worlds with immediate predecessors are exactly the ones inW0,so F0is the relativized reduct of F with respect to∃yRyx.

It is easy to see that F ⊨¬∀xRxx,F′⊭¬∀xRxx.

Finally,definef:F→F′such that every world is mapped tor,it is easy to see thatfis a surjective bounded morphic morphism,so FF′.

Therefore,CSeris stable.

4 Undecidability Results

In this section,we will make use of the stable class technique to show that certainL-definability problems with respect to certain frame classesare undecidable by showing thatisL-stable and that the validity problem of first-order sentences inis undecidable.

Theorem 7.The classCof all Kripke frames is LT-,LU-,LH-,LH(@)-stable.

Proof.Define:=Rx1x,β:=∃x∃y(x ／=y ∧¬∃zRzx ∧¬∃zRzy),then we can show that forLT-,LU-,LH-,LH(@)-stability,conditions 1 and 2 hold for C witnessed by

· For condition 1,since the class of all Kripke frames is closed under taking subframes,this condition is automatically satisfied;

· For condition 2,for any Kripke frame F0=(W0,R0)∈C,we can construct F and F′as follows:

We take an isomorphic copy F′′of F′,and define F :=F′ ⊎F′′,where the isomorphic copy ofsin the F′′part is denoted ass′;

It is trivial that F and F′ ∈

Since in F,the worlds who hassas an immediate predecessor are exactly the ones in the original copy(i.e.,F′part)W0,so F0is the relativized reduct of F with respect toRx1xands.

It is easy to see that F ⊨∃x∃y(x／=y ∧¬∃zRzx ∧¬∃zRzy),F′⊭∃x∃y(x／=y ∧¬∃zRzx ∧¬∃zRzy),since in F there are two worlds without immediate predecessor,but in F′there is only one world without immediate predecessor.Finally,definef:F→F′such that both the F′part and the F′′part are mapped to F′in an isomorphic way.Then it is easy to check thatfis a surjective tense bounded morphic morphism,a surjective bounded morphic morphism,F′is a generated subframe of F,so FF′forL ∈{LT,LU,LH,LH(@)}.

Therefore,C isLT-,LU-,LH-,LH(@)-stable.

Corollary 1.The L-definability problem inCis undecidable for L ∈{LT,LU,LH,LH(@)}.

Proof.By Theorem 5 and Theorem 7,it suffices to show that the validity problem of first-order sentences in C is undecidable,which is already shown in[4,Corollary 1].

Theorem 8.The classRef of all reflexive Kripke frames is LT-,LU-,LH-,LH(@)-stable.

Proof.Defineα():=Rx1x∧¬x1=x,β:=∃x∃y(x／=y ∧¬∃z(Rzx∧¬z=x)∧¬∃z(Rzy∧¬z=y)),then we can show that forLT-,LU-,LH-,LH(@)-stability,conditions 1 and 2 hold forRefwitnessed by(α(),β):

· For condition 1,since the class of all reflexive Kripke frames is closed under taking subframes,this condition is automatically satisfied;

· For condition 2,for any Kripke frame F0=(W0,R0)∈Ref,we can construct F and F′as follows:

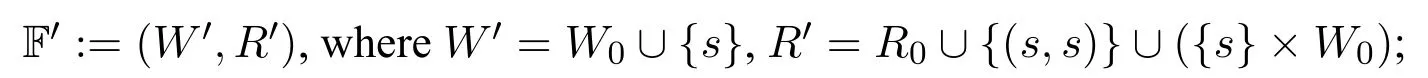
We take an isomorphic copy F′′of F′,and define F :=F′ ⊎F′′,where the isomorphic copy ofsin the F′′part is denoted ass′;

It is trivial that F and F′ ∈Ref.

Since in F,the worlds who hassas a strict immediate predecessor are exactly the ones in the original copy(i.e.,F′part)W0,so F0is the relativized reduct of F with respect toRx1x ∧¬x1=xands.

It is easy to see that F ⊨∃x∃y(x／=y∧¬∃z(Rzx∧¬z=x)∧¬∃z(Rzy∧¬z=y)),F′⊭∃x∃y(x／=y ∧¬∃z(Rzx ∧¬z=x)∧¬∃z(Rzy ∧¬z=y)),since in F there are two worlds without strict immediate predecessor,but in F′there is only one world without strict immediate predecessor.

Finally,definef:F→F′such that both the F′part and the F′′part are mapped to F′in an isomorphic way.Then it is easy to check thatfis a surjective tense bounded morphic morphism,a surjective bounded morphic morphism,F′is a generated subframe of F,so FF′forL ∈{LT,LU,LH,LH(@)}.

Therefore,CRefisLT-,LU-,LH-,LH(@)-stable.

Corollary 2.The L-definability problem inRef is undecidable for L ∈{LT,LU,LH,LH(@)}.

Proof.By Theorem 5 and Theorem 8,it suffices to show that the validity problem of first-order sentences inRefis undecidable,which is already shown in[4,Corollary 3].

Theorem 9.The classTra of all transitive Kripke frames,Ref,Tra of all reflexive and transitive Kripke frames,Poset of all partial orders are LT-,LU-,LH-,LH(@)-stable.

· For condition 1,these three classes are all closed under taking subframes,so this condition is automatically satisfied;

Corollary 3.The LT-,LU-,LH-,LH(@)-definability problems inTra,Ref,Tra,Poset are undecidable.

Proof.By Theorem 5 and Theorem 9,it suffices to show that the validity problems of first-order sentences inare undecidable,which is already shown in[4,Corollary 3,5].

Theorem 10.The classSym of all symmetric Kripke frames is LT-,LU-,LH-,LH(@)-stable.

Proof.Defineα(x,x) :=Rx1x,β:=¬∃x∀y(x=y ∨Rxy),then we can show that forLT-,LU-,LH-,LH(@)-stability,conditions 1 and 2 hold forSymwitnessed by(α(),β):

· For condition 1,since the class of all symmetric Kripke frames is closed under taking subframes,this condition is automatically satisfied;

· For condition 2,for any Kripke frame F0=(W0,R0)∈Sym,we can construct F and F′as follows:

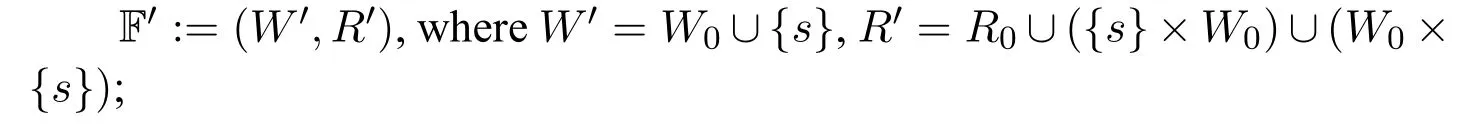
We take an isomorphic copy F′′of F′,and define F :=F′ ⊎F′′,where the isomorphic copy ofsin the F′′part is denoted ass′;

It is trivial that F and F′ ∈Sym.

Since in F,the worlds who hassas an immediate predecessor are exactly the ones in the original copy(i.e.,F′part)W0,so F0is the relativized reduct of F with respect toRx1xands.

It is easy to see that F ⊨¬∃x∀y(x=y ∨Rxy),F′⊭¬∃x∀y(x=y ∨Rxy),since in F′,any nonspoint is anR′-successor ofs,while in F,each point is not connected with a point in the other isomorphic copy.

Finally,definef:F→F′such that both the F′part and the F′′part are mapped to F′in an isomorphic way.Then it is easy to check thatfis a surjective tense bounded morphic morphism,a surjective bounded morphic morphism,F′is a generated subframe of F,so FF′forL ∈{LT,LU,LH,LH(@)}.

Therefore,CSymisLT,LU-,LH-,LH(@)-stable.

Corollary 4.The LT-,LU-,LH-,LH(@)-definability problem inSym is undecidable.

Proof.By Theorem 5 and Theorem 10,it suffices to show that the validity problem of first-order sentences inSymis undecidable,which is already shown in [4,Corollary 3].

Theorem 11.The classRef,Sym of all reflexive and symmetric Kripke frames is LT-,LU-,LH-,LH(@)-stable.

Proof.Defineα() :=Rx1x ∧¬x1=x,β:=¬∃x∀yRxy,then we can show that forLT-,LU-,LH-,LH(@)-stability,conditions 1 and 2 hold forRef,Symwitnessed by(α(),β):

· For condition 1,since the class of all reflexive symmetric Kripke frames is closed under taking subframes,this condition is automatically satisfied;

· For condition 2,for any Kripke frame F0=(W0,R0)∈Ref,Sym,we can construct F and F′as follows:

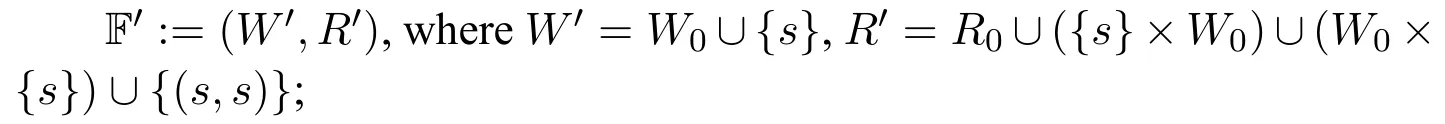
We take an isomorphic copy F′′of F′,and define F :=F′ ⊎F′′,where the isomorphic copy ofsin the F′′part is denoted ass′;

It is trivial that F and F′ ∈Ref,Sym.

Since in F,the worlds who hassas a strict immediate predecessor are exactly the ones in the original copy(i.e.,F′part)W0,so F0is the relativized reduct of F with respect toRx1x ∧¬x1=xands.

It is easy to see that F ⊨¬∃x∀yRxy,F′⊭¬∃x∀yRxy,since any point is anR′-successor ofsin F′,while in F,points in different isomorphic copies are not connected.

Finally,definef:F→F′such that both the F′part and the F′′part are mapped to F′in an isomorphic way.Then it is easy to check thatfis a surjective tense bounded morphic morphism,a surjective bounded morphic morphism,F′is a generated subframe of F,so FF′forL ∈{LT,LU,LH,LH(@)}.

Corollary 5.The LT-,LU-,LH-,LH(@)-definability problem inRef,Sym is undecidable.

Proof.By Theorem 5 and Theorem 11,it suffices to show that the validity problem of first-order sentences inRef,Symis undecidable,which is already shown in [4,Corollary 3].

5 Conclusions and Further Directions

In this paper,we use the stable class technique in[4]to show that certain extended modal definability in certain frame classes are undecidable.Here we use a frame construction of F and F′from F0which satisfies that F′is a tense bounded morphic image,a bounded morphic image,a generated subframe of F at the same time,so we can treatLT,LU,LH,LH(@)uniformly.

As we know,the more expressive the extended modal language is,the less kinds of frame constructions its validities are preserved under.Therefore,if we consider the hybrid languageLH(E)which has both the nominals and the universal modality,its validity is only preserved under taking ultrafilter morphic images(e.g.,see [6]),which makes it harder to construct F and F′.While for very expressive hybrid language likeLH(E)extended with the downarrow binder,each first-order formula isLH(E,↓)-definable.Therefore,it is an interesting question that for which positionLof the extended modal language hierarchy,theL-definability problem for first-order sentences becomes decidable.