一种基于二分法查找的改进混合蛙跳算法

王晓彬，邹海荣

（上海电机学院电气学院，上海 201306）

群体智能优化算法是通过模仿自然界中群居生物的觅食或生活行为，研究其中的原理，并应用数学方法建模尝试解决大量实际工程应用中的难题。由于其通用性强、原理简单、实现方便，最重要的是能有效解决各种传统方法不易解决的复杂的组合优化问题，通过多次迭代自我适应、学习和发展，最终得到一个复杂问题的最优解，受到了众多专家学者的青睐，开拓了许多新兴研究热点，取得了显著成功。

混合蛙跳算法（Shuffled Frog Leaping Algorithm，SFLA）通过模拟青蛙觅食行为［1］，进行元启发式搜索，从而得到问题的最优解。SFLA最早由Eusuff等[2]提出，相较于其他智能优化算法，其显著特点是采取局部搜索和全局信息搜索融合的协同搜索策略。该算法具有模因算法（Memetic Algorithm，MA）搜索效率和容错率高的优点，也有粒子群优化算法（Particle Swarm Optimization，PSO）通用性强的优点，是两者优点的结合体。SFLA参数少，更便于使用编程实现。目前已广泛应用于模式识别、函数优化、信号与信息处理等领域中，并取得了成功。

虽然SFLA优点众多，但会出现求解精度不高、算法易陷入局部最优等问题。针对这些问题，近年来，许多国内外学者对其进行研究、改进。高建瓴等［3］引入自适应同步因子，改变局部搜索蛙跳规则，从而增加种群的多样性。赵红星等［4］对青蛙的觅食机制和更新迭代公式重新定义，提高了SFLA的全局和局部搜索能力。王联国等［5］对初始种群引入Tent混沌改进，在最差个体更新中引入扰动的柯西因子，提高算法的寻优能力。戴月明等［6］在全局搜索中采取精英群自学进化机制，对精英空间进行精细搜索，提升全局搜索能力。上述文献虽然通过一些方法提升了算法的寻优能力和收敛精度，但效果不是很理想，并没有考虑更优个体可能存在于其附近空间［7］。因此，本文提出一种基于二分法查找的改进SFLA，以最差蛙之外的其他个体的平均值作为中间因子，加强最差蛙与其他个体的交流，增强算法寻优能力和收敛精度；在标准蛙跳算法步长更新的基础上引入加速因子，提高算法的收敛速度；最后通过测试函数验证改进算法的有效性。

1 SFLA

1.1 算法原理

SFLA的背景是在一片沼泽地里，青蛙利用沼泽地中离散分布的石块去寻找更多食物［8］，每只青蛙个体之间通过交流来交换信息，通过整个种群的信息交流，使每只青蛙得到最多的食物。转换为算法的思想，即为了每个解都达到最优，最终使整个算法达到最优解，即由局部最优到全局最优的过程［9］。

由上述背景可得SFLA的基本思想：随机生成M只青蛙个体，组成初始种群P=｛X1，X2，…，X M｝，s维解空间中的第i只青蛙可表示为Xi=（x i1，x i2，…，x is）。在生成初始种群之后，首先对青蛙个体进行排序，即求解种群内所有青蛙个体的适应度值，并按照大小降序排列，将种群中最优适应度值（最小值）记为Xglo。然后将种群依据规则分成一个个小的子种群，平均分成m个，每个子种群包含n只个体，它们的关系M=m×n。其中，第1只青蛙分入第1个子种群组，第2只青蛙分入第2个子种群组，继续分配，第m只青蛙分入第m个子种群组，第m+1只青蛙重新分入第1个子种群组，以此类推，平均分配[10]。将每个子种群中的最好适应度（最小值）的青蛙记为Xb，最差适应度的青蛙记为Xw。最后根据分好的子种群组，依据更新策略进行位置的更新，即对子种群组中的Xw循环进行局部搜索操作。其更新方式为

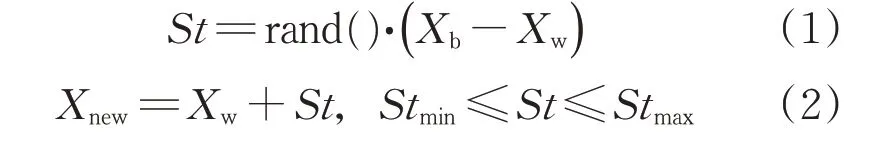
式中：rand（）函数表示产生0～1之间均匀分布随机实数；Stmin、Stmax为最差蛙所允许改变步长的下限和上限。

算法经过上式更新后，若得到的蛙Xnew优于原来的蛙Xw，则取代原来子种群组中的蛙；若没有改进，用Xglo取代Xb，算法再次更新最差蛙的位置；若此次更新后，适应度仍然比更新前的值差，则随机取种群中任意一个青蛙个体来取代原来的Xw。当局部搜索次数达到所允许的上限时，将所有子种群组内的青蛙重新混合，重复上述优化过程［11］。如此反复，直至达到全局最大收敛次数为止。图1为SFLA流程。

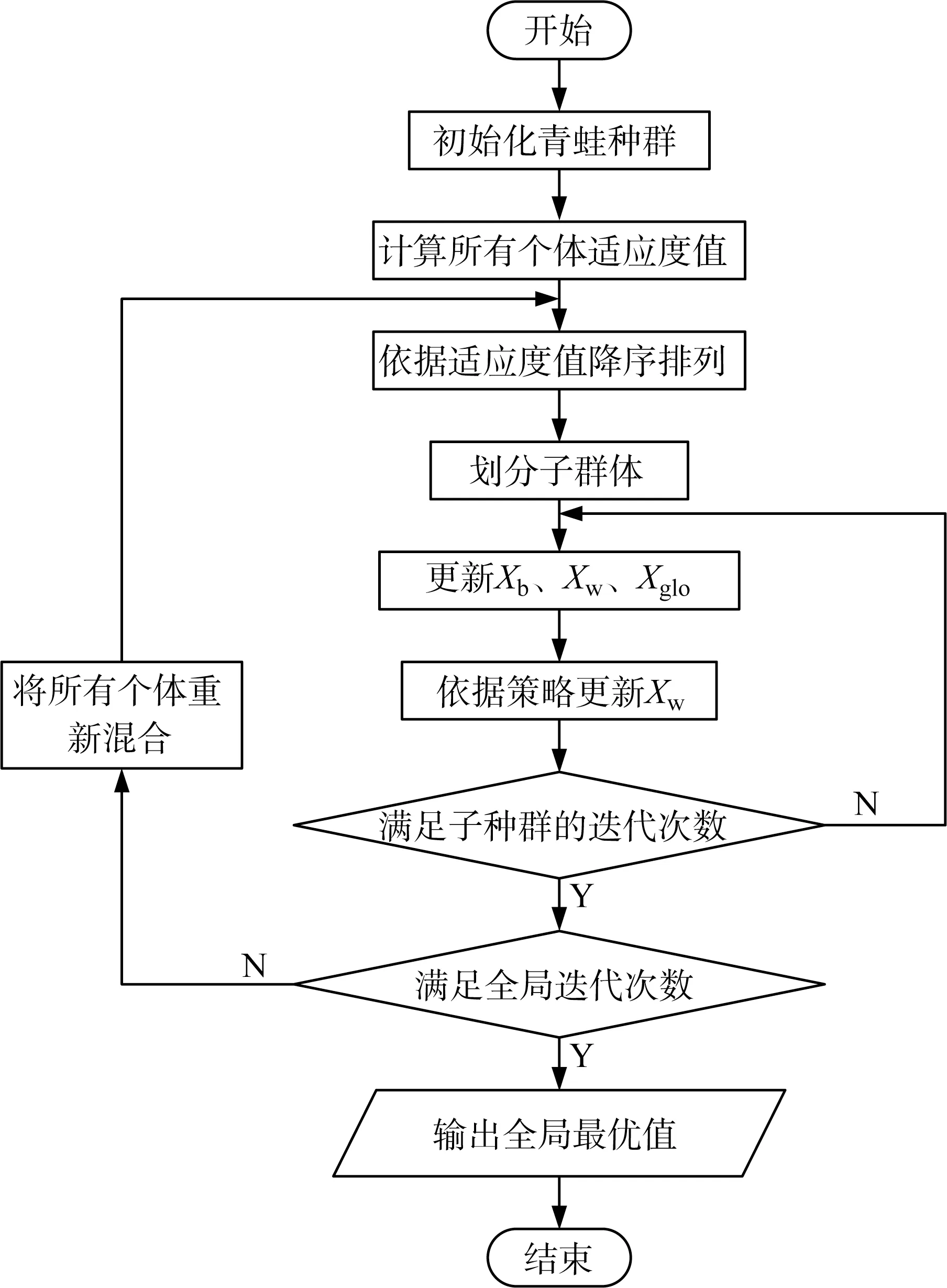
图1 SFLA流程

1.2 改进的SFLA

从SFLA的基本思想来看，SFLA以子种群中最差蛙为更新基础，将最优和最差蛙之间的位置差值作为更新的步长，更新最差蛙向食物靠近。最差蛙的每一次位置的更新只与子种群内或者种群内的最优青蛙个体交换信息，并没有与其他个体进行充分的信息交换，忽视了与其他蛙的信息交流，使得交流趋向单一化，导致青蛙个体之间的互异性减小，缩减了解的搜索空间，导致种群易陷入局部最优而早熟收敛，达不到所要求的精度［12］。

在种群个体位置更新过程中，基于数学中二分法查找的思想，引入中间因子和加速因子。通过引入中间因子，调控青蛙个体在寻优过程中的步长，扩大算法的局部搜索范围，从而保持青蛙种群的多样性；引入加速因子，加快蛙的搜索速度。

1.2.1 引入中间因子二分法查找是一种高效的搜索方法，其基本原理是：数据按升序（或者降序）排列，对于一个给定值X，从序列的中间位置开始比较，若当前位置的值等于X，则查找成功；若X小于当前位置值，则在数列的前半段中查找；若X大于当前位置值，则在数列的后半段中继续查找，直到找到为止［13］。

基于二分法查找的思想，针对SFLA的缺点，提出如下改进：在对蛙群排序后，除最差蛙之外的其他个体的平均值作为中间因子Xa。之后重新混合，将其分为两个子种群mX1、mX2，记种群mX1的平均值为Xave1，种群mX2的平均值为Xave2。若将Xave1与中间因子比较，适应度比中间因子所对应的适应度差时，则淘汰该种群，选择未淘汰的种群更新最差蛙。之后在未淘汰的种群内重复上述操作，具体的位置更新策略如下：

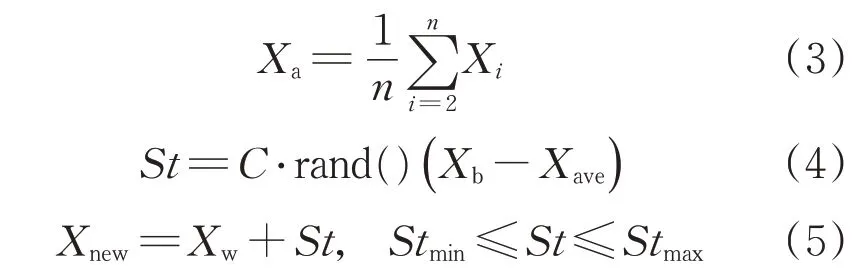
式中：Xi为青蛙种群中不同于Xw的青蛙个体；C为加速因子。

引入中间因子Xa调整最差蛙，向Xb进化，不忽略其他潜在优秀个体的信息。当系统突然受到外界干扰时，因其群体数量多且均参与其中，使系统的稳定性得到提升［14］。

1.2.2 引入加速因子在算法中，步长的大小会影响算法的性能。若步长过小，会减弱算法搜索的能力；若步长过大，则会跳过真正的最优解，陷入局部最优。在SFLA中，如式（1）所示，步长是rand（）函数产生的0～1的随机数与位置差值的乘积。本文改进算法引入大于1的加速因子C，如式（4）所示，在SFLA的步长基础上增大步长，加快局部收敛速度。选择合适的加速因子，使算法在搜索时能以合适的变化率平稳地进行［15］。

2 仿真实验及结果分析

2.1 实验设置

为了验证改进混合蛙跳算法（Improved Shuffled Frog Leaping Algorithm，ISFLA）的有效性，选取以下6个典型测试函数，对ISFLA的性能进行仿真研究。各函数的表达式如下：

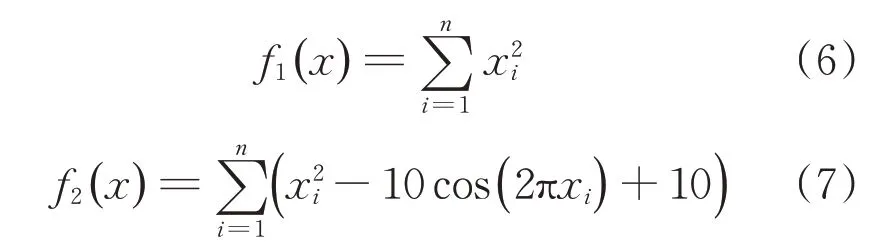
各函数的参数设置见表1。

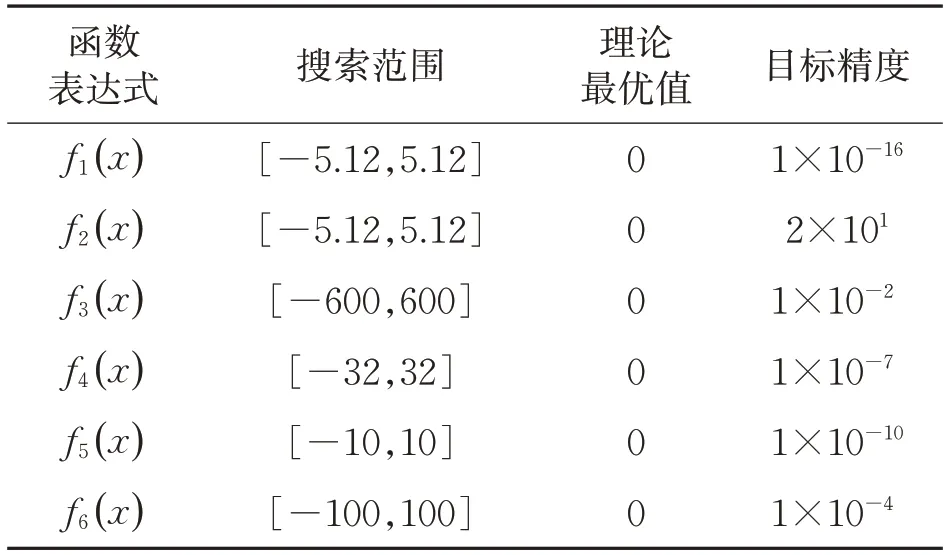
表1 测试函数参数设置

本文将6个测试函数的解空间的维数都固定为30维，设计了3个实验［16］。首先是加速因子确值实验，改变加速因子的值，观察数值的大小对算法收敛速度的影响；其次是算法收敛精度实验，固定算法最大迭代次数为500次，比较算法独立运行后的收敛精度和运行时间；最后是算法迭代次数比较实验，指定各函数收敛精度，对两种算法的进化次数进行对比［17］。

2.2 加速因子确值实验

加速因子虽然能够加快收敛速度，但不是越大越好。为了确定不同加速因子对算法收敛速度的影响，在改进蛙跳算法的基础上，分别记录加速因子不同的值达到最大迭代次数所用的时间以及达到收敛精度所用的时间，确定加速因子最佳值并应用于算法收敛精度实验。加速因子确值实验结果如图2所示。对函数f1～f6，加速因子分别取不同的值，算法在达到最大迭代次数时记录的时间如图3所示。

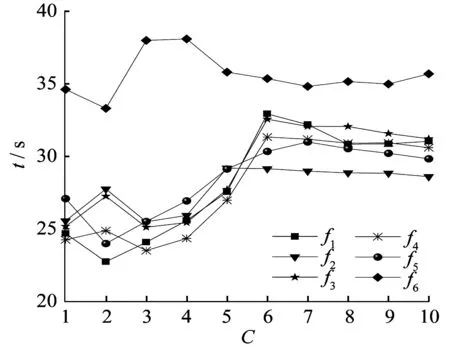
图2 加速因子确值实验结果

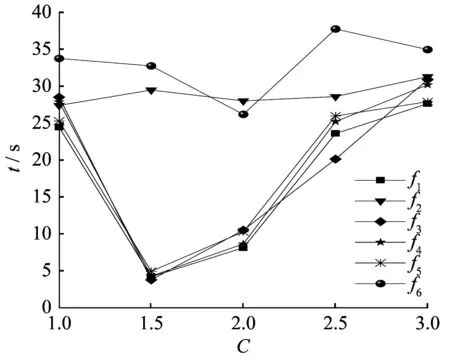
图3 达到收敛精度的时间记录图

由图2可知，当加速因子小于3时，时间均在30 s以内（除了函数f6），时间较短；当加速因子超过3，且迭代次数在子种群所允许的最大迭代次数内，时间均在32 s上下且变化基本不大。由此可知，加速因子的取值应该控制在1～3之间。由图2、图3可知，当加速因子C位于1～3时，算法达到最大迭代次数所花时间与取其他值相比所花时间短，而且当加速因子C取1.5时，除函数f2和f6，此时算法达到收敛精度所花的时间是最短的，故综合考虑，加速因子C的取值确定为1.5，并应用于算法收敛精度实验和算法迭代次数比较实验。

2.3 算法收敛精度实验

算法收敛精度实验设置青蛙种群个体总数P=200，子种群数量m=20，每个子种群中青蛙个体n=10，子种群内最大进化迭代次数为10次，全局最大进化迭代次数为500，最优解空间的维数为30，算法独立运行30次，得到的实验结果如表2所示，函数平均值进化曲线如图4～图9所示［18］。

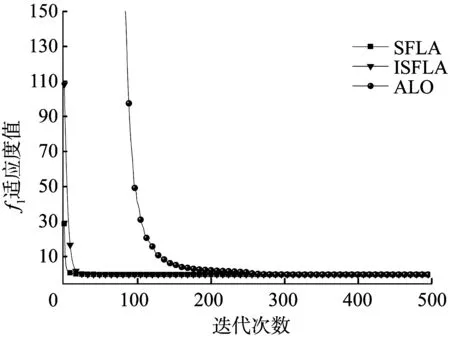
图4 函数f1平均值的进化曲线

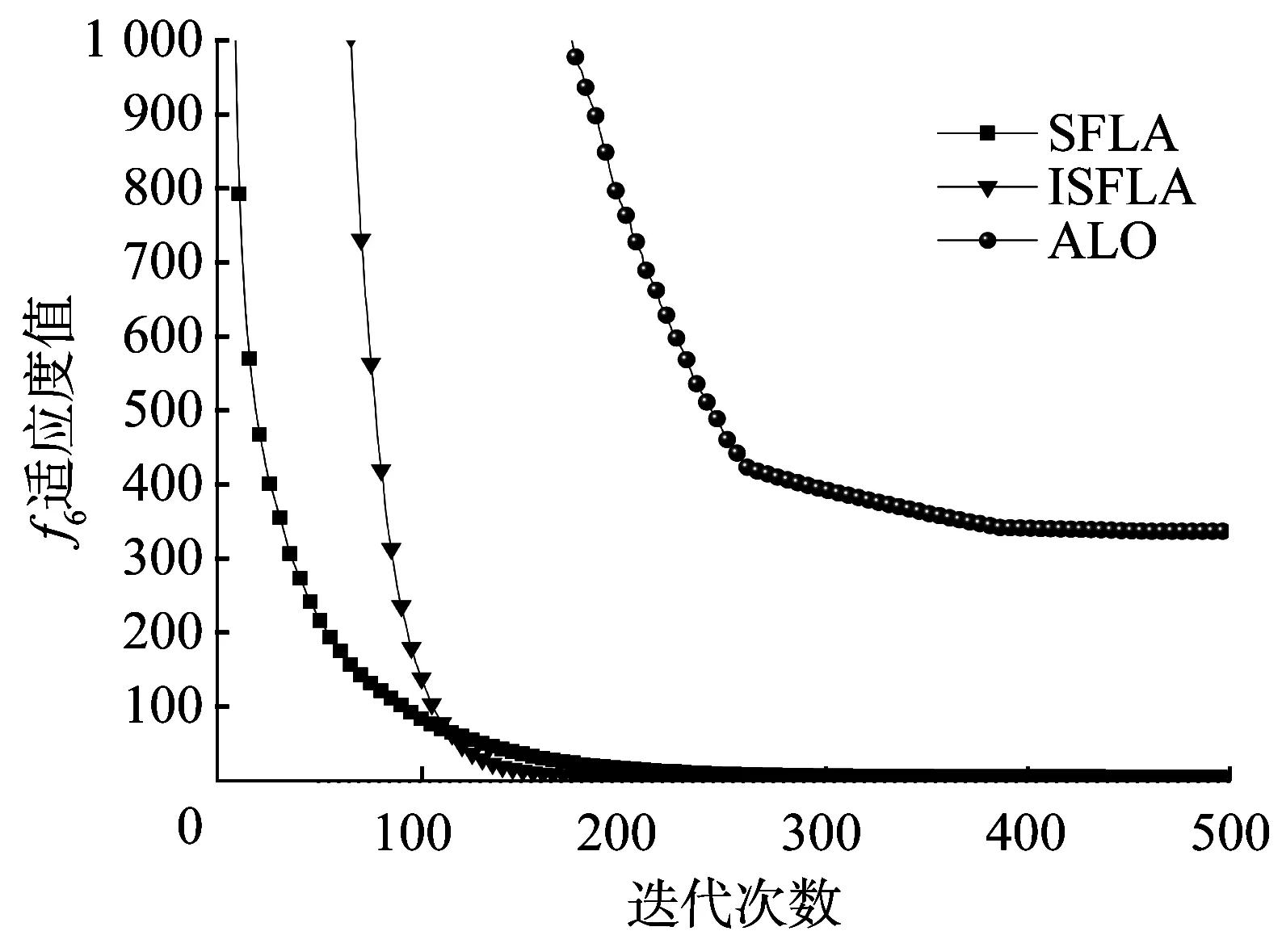
图9 函数f6平均值的进化曲线

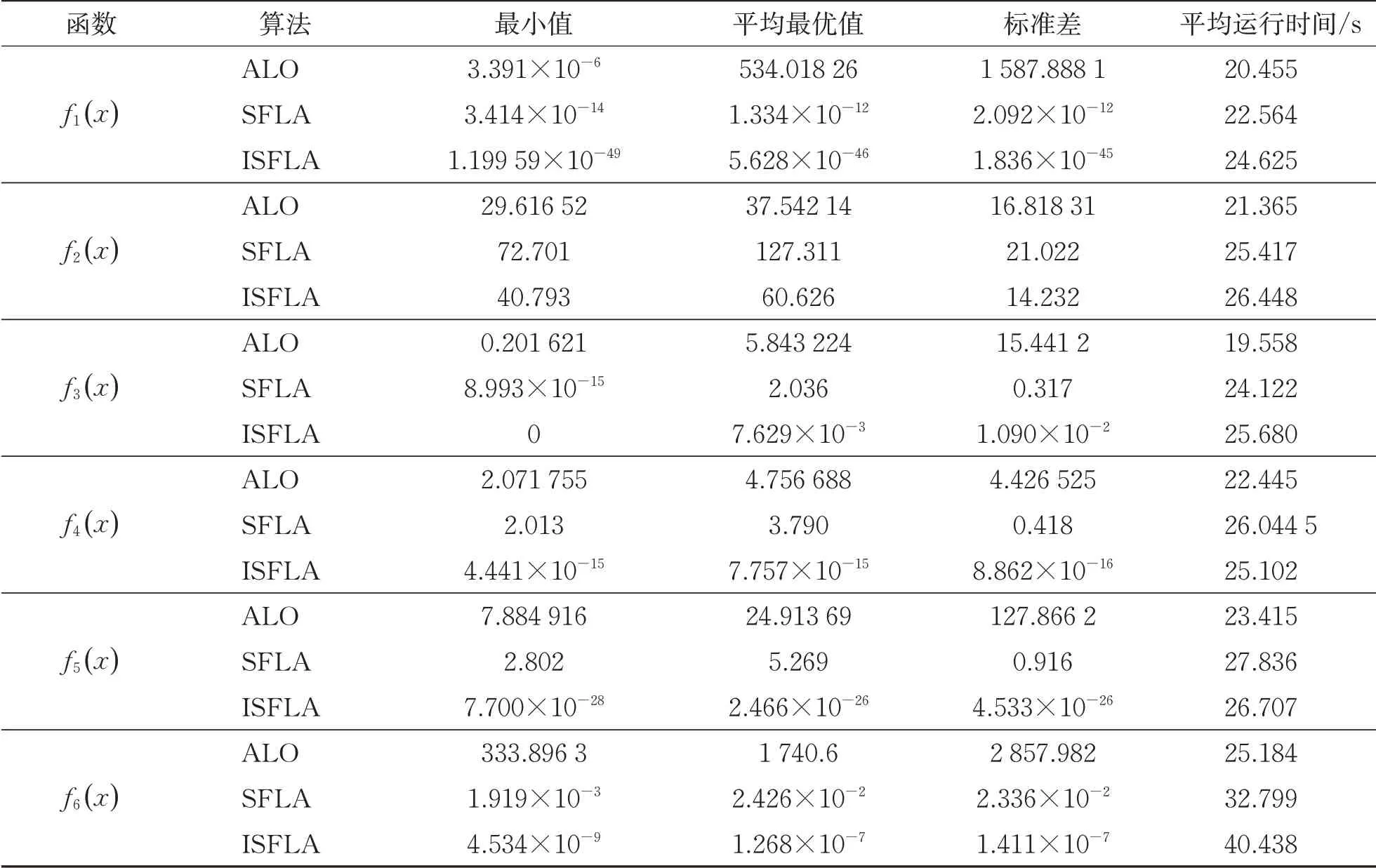
表2 算法收敛精度的实验结果

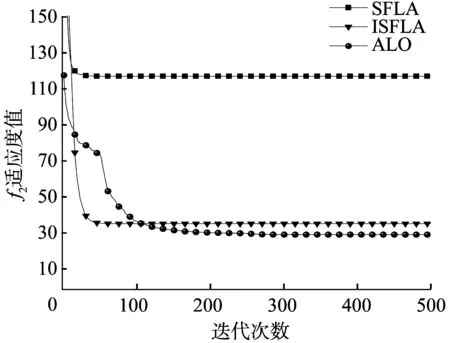
图5 函数f2平均值的进化曲线

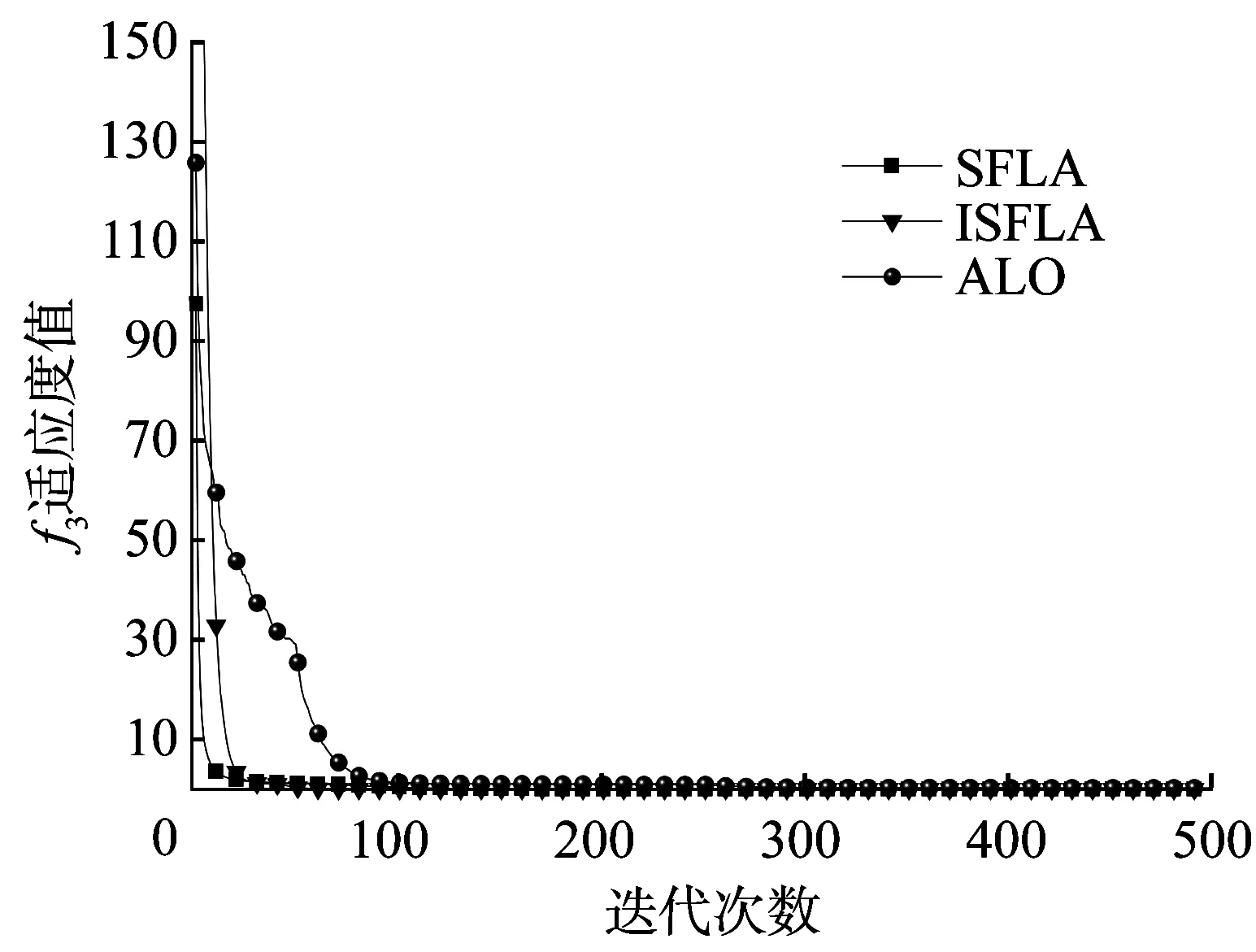
图6 函数f3平均值的进化曲线

图7 函数f4平均值的进化曲线

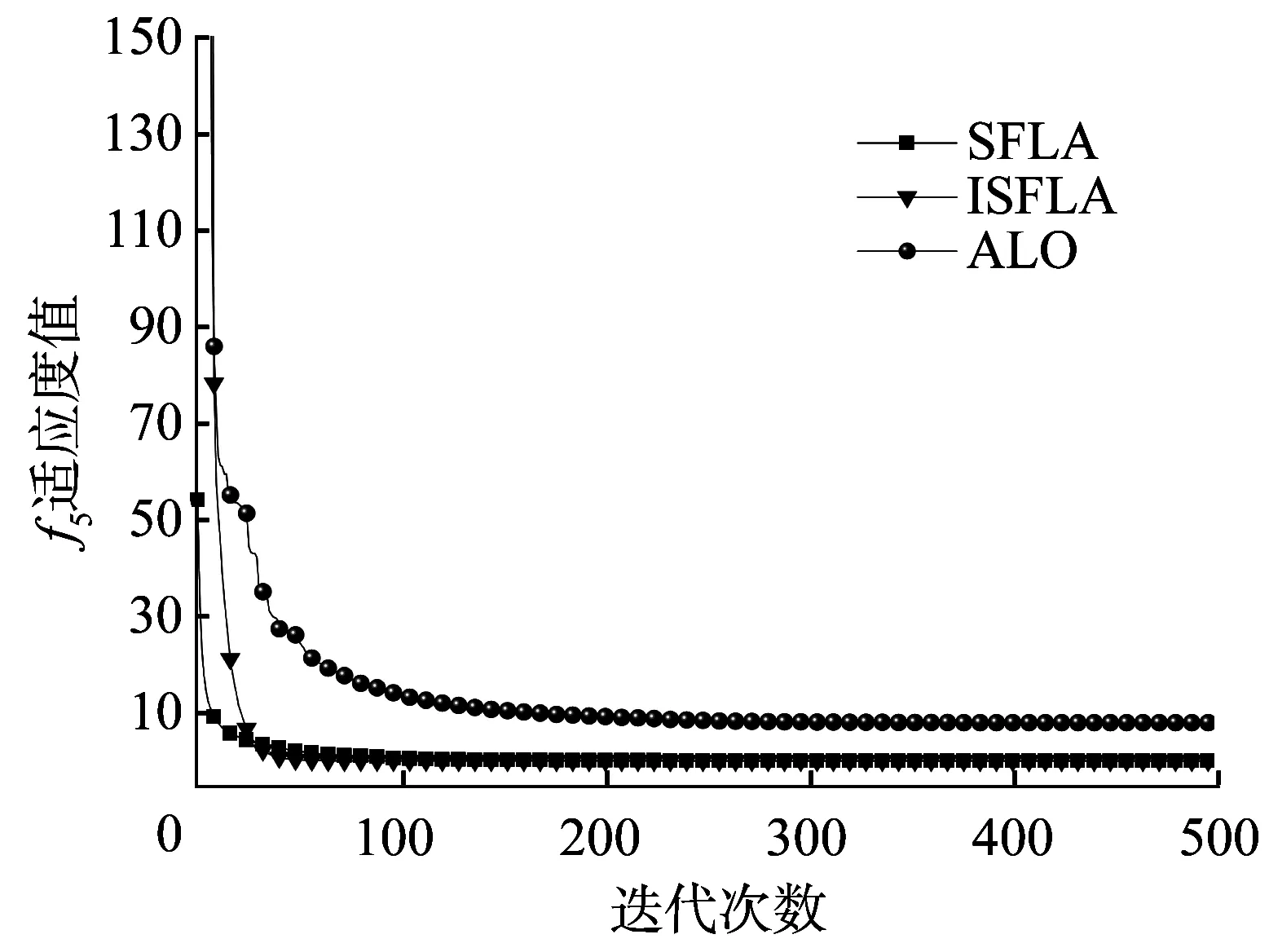
图8 函数f5平均值的进化曲线

从表2可以看出，ISFLA对6个测试函数的寻优精度均优于SFLA和蚁狮算法（Ant Lion Optimizer，ALO）；与SFLA相比，对函数f1、f3、f4、f5、f6的收敛精度明显提高；对函数f2虽然没有明显数量级上的提升，但是无论是收敛精度最小值还是平均最优值都有近1倍的减少，且优于SFLA和ALO。从标准差来看，ALO算法标准差较大且不稳定；改进后的算法标准差相对较小，在稳定程度上要优于SFLA和ALO。从图4～图9可以看出，虽然ALO算法收敛速度快，但是收敛精度却达不到要求；ISFLA在迭代前期可能速度较慢，但是在进化50次左右后，收敛速度明显比SFLA快，且能较快地得到最优解。

2.4 算法迭代次数比较实验

实验指定6个函数所要达到的收敛精度。设置子种群内青蛙数n=10，子种群内最大进化次数为10，全局最大进化迭代次数仍然设置为500。若算法迭代到所要求的最大迭代次数后，仍没有达到指定的精度，则认为算法该次没有收敛，算法同样独立运行30次［19］。表3为算法迭代次数比较实验的结果（成功率=达到指定精度的收敛次数/总实验次数）。

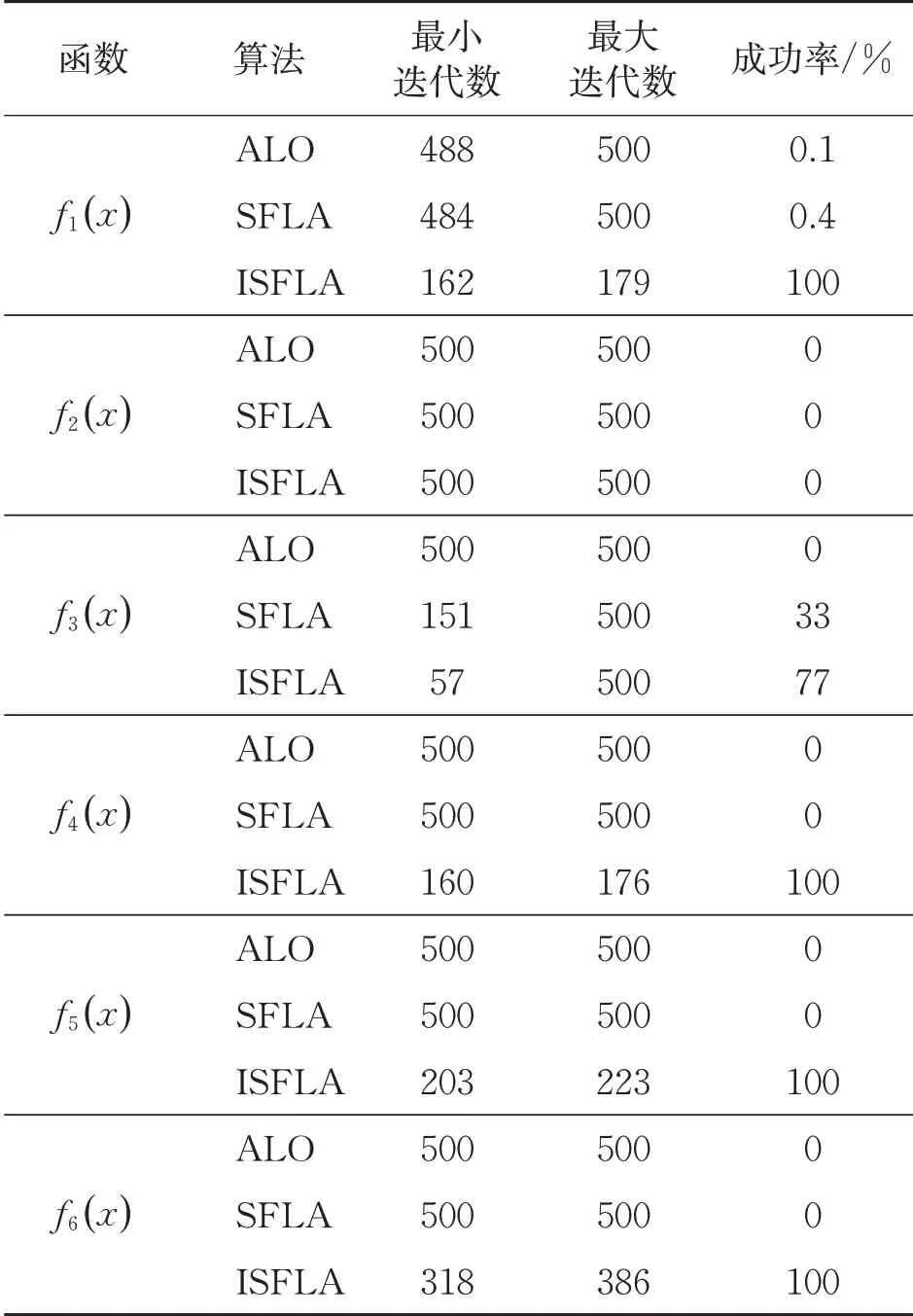
表3 迭代次数比较实验的结果

从表3可以看出，对函数f2的求解，ALO、SFLA和ISFLA均没有在固定迭代次数达到收敛精度，但是由算法收敛精度实验可知，ISFLA在有限迭代次数里得到的最优解要比SFLA优1倍；对函数f1的求解，虽然ALO和SFLA也能达到收敛精度，但是成功率较低；对于其他函数的求解，ISFLA达到收敛精度的迭代次数明显比SFLA和ALO低，成功率明显高于SFLA和ALO。

3 结 论

本文在提出的ISFLA基础上，引入了中间因子和加速因子，解决了标准算法在优化过程中出现的求解精度不高、收敛速度慢等缺陷。在局部搜索的寻优过程中，改变步长更新策略，增加种群的多样性，拓宽了最优解的搜索范围。通过使用6个30维测试函数，分别设置算法收敛精度实验和算法迭代次数比较实验进行对比分析，并与ALO算法比较，表明改进的算法在收敛精度和收敛速度方面更加突出，寻优性能相较于标准算法也有较大提升。