基于三维实景与BIM模型的土方工程分区调配方法研究

胡 滨 张 勇 刘 颖 黎 娆

(1.山推工程机械股份有限公司，济宁 272073； 2.武汉市市政建设集团有限公司，武汉 430023；3.华中科技大学土木与水利工程学院，武汉 430074)

引言

早在1981年，Mayer和Stark教授就提出并构建了土方分配的线性规划数学模型，可用于解决传统土方积累图不再适用的问题。直至2016年，Chaojue Yi等采用混合整数线性规划(MILP)模型为基于网格法的临时道路土方作业生成了最优布局解决方案。廖婷等于2017年针对考虑了土方性质的黄高填土调配提出了动态的优化调度算法，改进了多目标资源分配的问题求解方法。邓朗妮等于2018年提出通过Civil 3D软件精确计算土方量并通过运筹学建立多元多约束条件的数学模型，得到可行性的土方调配方案[1]。

目前土方调配方案的确定仅凭借工程师个人经验，根据就近原则只能保证局部最优而没有综合考虑各个挖填方区土方量和运距等参数对土方调配方案的影响，此外调配准备工作、调配区土壤类别、场地清理费用、入场施工现场施工道路建设以及维护等要素也需要综合考虑全局最优[2]。

自1956年美国麻省理工Miller教授提出数字地面模型的概念后，数字高程模型(DEM)在测绘、军事、遥感中的应用越来越广泛[3]。近年来随着GIS、测绘学的发展，建立高精度可视化的DEM模型可完成建筑场地的实景重建，实现实时查询地面任意点高程[4]。侯铁等基于遥感卫星影像和数字高程模型构建三维地形场景路线，应用于市政工程项目中，实现了辅助项目规划设计、方案比选和景观审查以及可视化交互的效果[5]。

在断面法、格网法、等高线法、DTM等传统土方量计算方法的基础上，基于规则格网的DEM模型和基于不规则三角网的DEM模型也越来越多地被应用于土方工程量计算中，并且其计算效率和精度都优于传统计算方法[6]。采用定向数字高程模型的方式构造数字高程模型实现了精度更高、成果更细致的计算方法，为大面积不规则区域的土方计算工作提供了一种切实可行的方法[7]。黄富强等基于数字高程模型实现了在大型工程中土石方量的准确快速计算，通过精度比对分析，表明数字高程模型适用于各种地形的土石方量计算[8]。

基于以上研究，目前已经实现了利用DEM进行土方量的计算，但并未实现计算准确化和利用到土方调配工作中。现提出基于无人机扫描技术进行三维实景与BIM模型比对获取土方工程量，并在此基础上进行全局土方合理调配的研究问题，该研究以某机场项目为实例，进行了土方调配方案的设计和比对。该研究一方面利用无人机扫描进行实景建模能够可视化土方调配进展，另一方面三维实景模型与BIM模型比对提高了土方量计算的准确性。

1 基于三维实景模型的土方量计算方法

首先通过利用无人机进行场景的全过程拍照，利用深度相机完成场景的记录实现全景建模，并与已经形成的BIM模型进行比对，完成土方分区的划分和土方量的准确计算。利用三维实景模型进行土方计算的精度远远高于传统方法，综合考虑了设计以及现场场地的实际情况，土方量的准确计算是进行土方调配的基础，能够保证土方调配方案的合理性和准确性。

1.1 土方工程三维实景模型建立思路

三维实景建模的关键是获取场区的全景图像，除了利用扫描仪对原始地图数据进行扫描，还可利用无人机拍照扫描施工场区获取场景基础数据。采取无人机拍照扫描的方式能够避免等高线不闭合、等高线内插造成的衔接误差等问题[9]； 同时利用无人机采集的点云数据具有的精度高、密度大等优势，还能够提高建模精度、自动完成场景信息的提取，提高可信度[10]。

利用搭载相机传感器的无人机从垂直和倾斜等不同角度进行场区的拍照，获取场区的图像和纹理数据，为形成原始地形图提供基础数据。同时利用厘米级的RTK导航定位系统和高性能成像系统，保证在照片成像时自动记录自身的镜头标定参数，结合照片的POS数据以及控制点信息，对提取的信息进行细化，将图像信息转化为计算机能够识别的矢量点云图，通过设立统一坐标点进行矢量点的位置变换，将最终细化的矢量信息进行矢量到栅格的转换。但是在进行无人机扫描和拍照过程中会不可避免地出现测量误差和系统误差，例如镜面反射、遮挡物遮挡、场区表面粗糙不平等各种因素，这些因素会使得获取的点云数据中不可避免地出现噪声点，因此在对点云数据进行处理之前需要利用平滑滤波进行手动的去噪与平滑工作，以得到有效点云[11]。对有效点云采用不规则三角网进行迭代处理，分类得到地形点和非地形点，并按照拟合误差最小为目标函数选择拟合精度贡献大的点云进行拟合，得到有效可靠的实景点云图[12]。

最终利用地形图和点云模型，通过计算机的精细化处理和根据自动矢量化的相关步骤以及高效率的实景建模技术，迅速构建出具有准确地理位置及高精度尺寸的实景三维模型。

1.2 三维实景模型与BIM模型比对获取精准土方量

传统土方量计算一般采用方格网法、三角网法、断面法、等高线法等，具有计算场地局限性、计算量大、计算精度较差等缺点。

本文提出了通过建立三维实景模型，进行将三维实景模型与BIM模型比对获取精准土方量的方法，不仅减少了计算工作量，提高了计算精度，减少了现场测量原始地形等数据的工作量，也提高了计算准确度和精度，并将其应用于某机场项目进行验证。

通过收集或无人机扫描获取的地形数据建立基础资料数据库并生成DEM，将三维实景模型与依据建筑工程项目的设计图纸绘制的BIM模型进行综合比对，考虑实际情况和根据场地平整和土方划分原则进行项目调配区的划分，在两种模型对比的基础上选取分区的土方进行土方量的自动计算。依据设计图纸并利用Revit、南方CASS、Civil3D等软件进行原状地貌和实际地面的数据输入，为了加强地形精度弥补地形变化复杂、等高线缺失等问题，可增加相应补测点，进行方格网数据的相互补充，以保证BIM模型的准确性和可参考性[13]。在创建好三维曲面模型之后需要进行三维模型检查，观察得到三维曲面模型是否有异常，避免因为数据添加错误而出现的曲面。在利用设计标高等设计数据的基础上建立场地平整完工后的模型，并在现场实景建模的基础上进行两种模型的比对，得到不同分区的土方施工量以及选定土块的土方量。

传统土方量计算方法仅仅根据二维图纸，缺乏对施工场地的实际情况考虑，因此计算精度较低。通过比对，完善分区的划分界限，充分考虑实际场地情况，建立三维实景模型以提高土方量的计算精度，达到土方工程量准确计算的目的，为土方调配的合理性提供了保障。

2 土方工程量调配方法研究

2.1 实施技术路线

土方调配设计就是确定土方的调配量和运输路线，具体包括：根据项目图纸在道路拐弯处划分或按照结构形式划分土方调配区，再将项目现场的三维实景模型和BIM设计模型进行比对，获取各个调配区的土方量，经过验证确定最终挖填方量；其次，根据挖填方的体积以及填方土块和挖方土块的重心距离来计算挖填方调配区之间的平均运距，形成土方运距图，选取合理的线性规划模型建立数学模型分析求解调配方案，以保障挖方和填方尽量达到平衡，减少重复倒运，最终发布施工决策，具体的技术路线如图1所示。

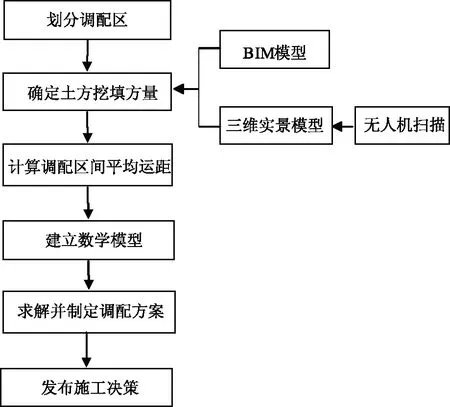
图1 技术路线图

2.2 土方工程量调配模型

运筹学提供了许多运用数学模型解决线性规划实际问题的数学算法，例如运用图解法可以解决变量较少的最大最小值问题； 动态规划可以解决资源分配问题等； 表上作业法可以解决工程中的产销平衡问题等。

在土地平整项目中，要力求使挖方量和填方量基本达到平衡，在挖方的同时进行填方，减少重复倒运。挖填方量与运距的乘积之和尽可能为最小，即运输路线和路程合理，运距最短，总土方运输量或者运输费用最小。因此，考虑以上限制条件，将填挖方量与运距的乘积之和设为目标函数，在尽可能满足挖填平衡的条件下采用线性规划求解最优土方调配量与路径。针对土方调配的多变量问题，最终采用运筹学的单纯形法建立解决土方调配的数学模型。

土方调配的目标函数是为了保证土方运输量与土方运距的乘积最小，并在最大程度上保证场区内部挖填平衡的约束条件下建立数学模型。考虑到工程建设项目场区内有n个挖方区域和m个填方区域，分别用i，j表示挖方区域和填方区域的编号； cij表示从第i个挖方区到第j个填方区的距离； xij表示从第i个挖方区域调配到第j个填方区域的土方工程量。则目标函数Z为：

约束条件为：

其中，an，bm分别表示挖方区和填方区的挖方量和填方量。

3 机场土方调配应用实例

3.1 某机场项目背景介绍

现以一在建机场项目为实例，进行土方调配方案的优化设计。该机场位于湖北省，距长江左岸约500m，场地地形平坦，地面标高22.88～23.86m，最大相对高差0.98m。该项目主要是满足某机场的改扩建工程，机场项目场地图如图2所示，按照结构形式分为停机坪、垂直联络道、平行滑行道、跑道等，根据现场的实际情况、设计要求、结构形式同时为了满足施工和分包的要求，最终划分为了13个分区，现根据图纸分区进行土方调配方案的制定。

图2 机场项目场地图

3.2 三维实景与BIM模型比对分区土方量结果

该机场项目现场较为空旷，无屋檐和树木遮挡，因此无人机采集数据方案实施较为顺利，经过无人机采集和计算机能够生成项目现场三维实景模型。在三维实景模型中通过手动框定区域并输入相应的标高，能够计算出选定区域相对于标高的体积差异。此外，将两个扫描模型对齐可以实现对体积差异超过一定阈值的区域进行高亮显示，直观可视化地展示出选定区域的体积差异，土方量计算精度可达到0.001m3，远远高于利用图纸计算的传统方法。

现以机场的部分土方计算为例，在已建立好的三维实景模型中手动框选闭合的土方区域，通过输入真实尺度进行尺度的恢复，以保证土方计算量的准确性，并根据BIM设计模型查找相应点的设计标高，输入标高，自动完成圈中区域的土方体积计算，计算结果如图3所示。

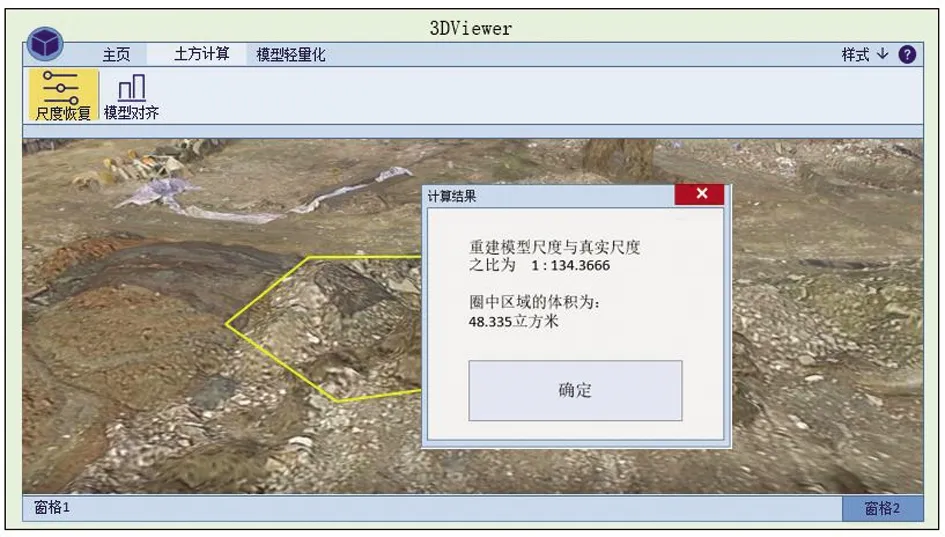
图3 三维实景土方量计算示意图

除了能够计算框选区域的土方体积，还可以进行两个扫描模型重叠体积的计算，可形成比对结果，能够达到土方施工进度的实时监控。将前后两次的扫描模型导入并进行对齐，保证同一区域部分点的匹配与重合，即可完成体积差的计算，土方计算体积差的精度依然可以达到0.001m3，这是传统方法无法达到的，比对土方计算结果如图4所示。

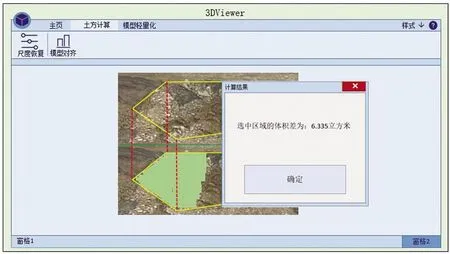
图4 土方量比对结果

3.3 土方调配最优方案设计与确定

项目管理者需要根据场地完成土方区域的划分，确定挖填方区，利用网格法划分成20m×20m或者40m×40m的小方格，并测量出每个小方格角点的实际标高与设计标高进行比对，计算出施工高度。在此基础上利用传统的CAD图纸或者DEM数字高程模型计算出每个方格的挖填方量，最终确定各个土方分区的挖填方量。确定各个土方分区的土方量是土方调配的基础，也是土方施工中计算量最大的一部分。

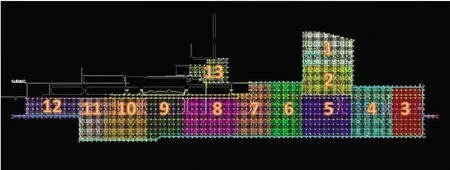
图5 机场土方分区划分示意图

根据项目图纸将汉南机场的施工场地划分为了13个土方调配区域，土方分区示意图见图5，其中3、5、9、10、11、12、13为挖方区，1、2、4、6、7、8为填方区，共计7个挖方区，6个填方区。各区域的挖填方量以及总方量如表1所示，各个土方分区之间的运距如表2所示。

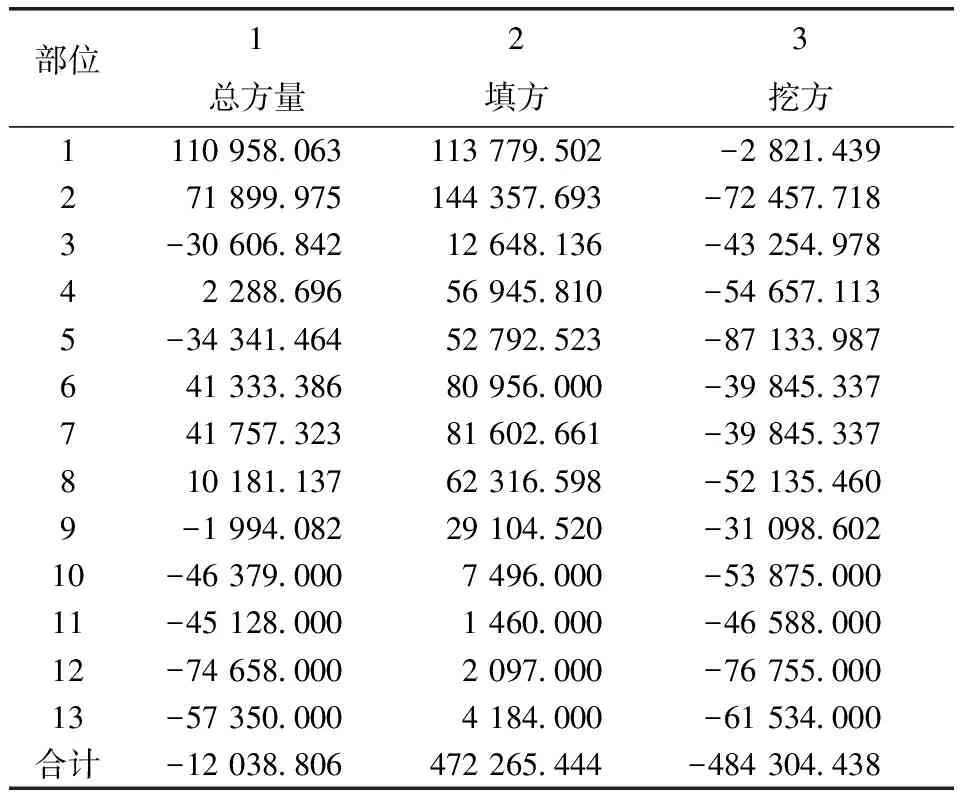
表1 土方分区挖填方量计算结果

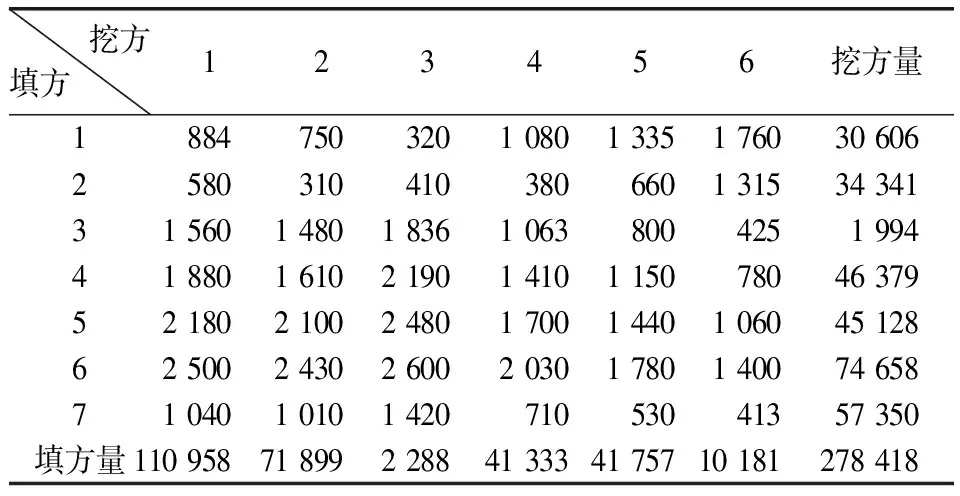
表2 土方运距图

在此基础上，利用上述数学模型建立土方调配的目标函数以及约束条件。

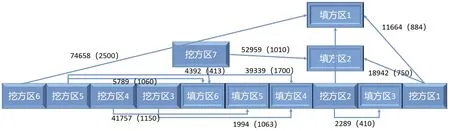
图6 土方调配方案示意图

通过计算可知，该项目场区内部的总挖方量为290 457.389m3，总填方量为278 418.582m3，很明显该机场项目的场区内部挖填土方量不平衡，因此需要根据挖填平衡原则进行约束条件的改进。由于填方量小于挖方量，因此首先满足内部填方量的需求，再将多余土方进行弃土，改进的约束条件如下所示：

由于计算量较大，因此利用Matlab中的linprog函数计算出土方调配的结果，如表3所示，为更好地展示计算结果，保留整数部分，函数形式如下：

最终根据该机场的场地划分的分区形成可视化的土方调配方案如图6所示，其中数字代表土方调运工程量，括号内数字代表两个区域之间的运距。该土方调配方案是在综合考虑了场地内各个分区的土方运距和土方量的基础上，以实景建模和BIM模型比对精准获取分区土方量为基础，利用线性规划模型求解土方调配的最优方案，通过Matlab进行数据计算，得到以上的土方调配方案。其中利用三维实景模型进行土方量计算的精度达到0.001m3，远远高于利用二维图纸计算。为该机场项目的土方调配提供了一种尽量满足项目内部挖填平衡、全局优化的调配方案。

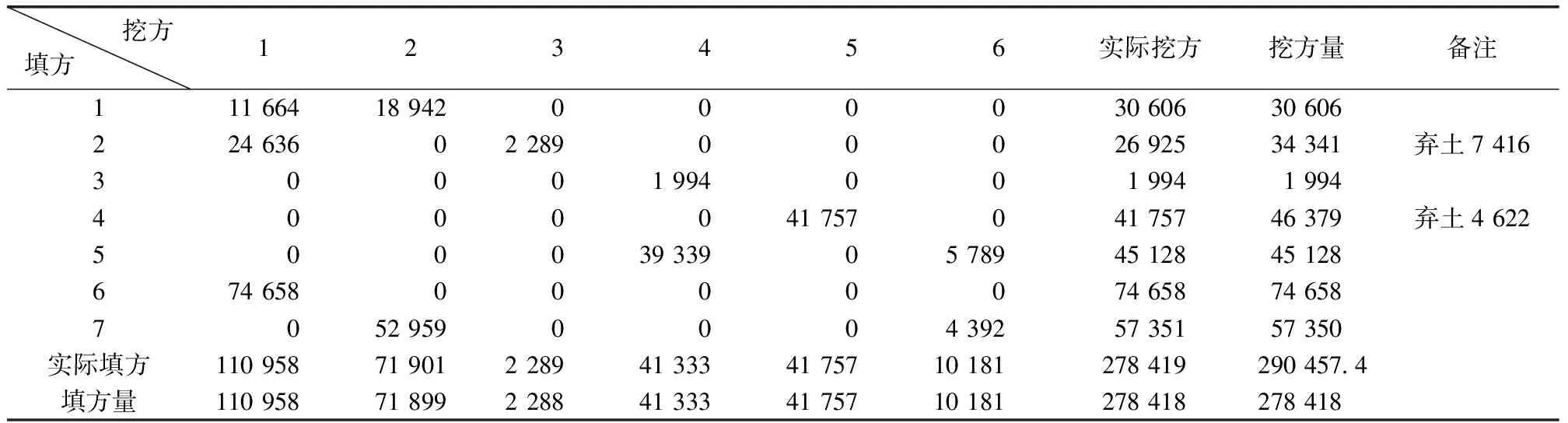
表3 最优土方调配

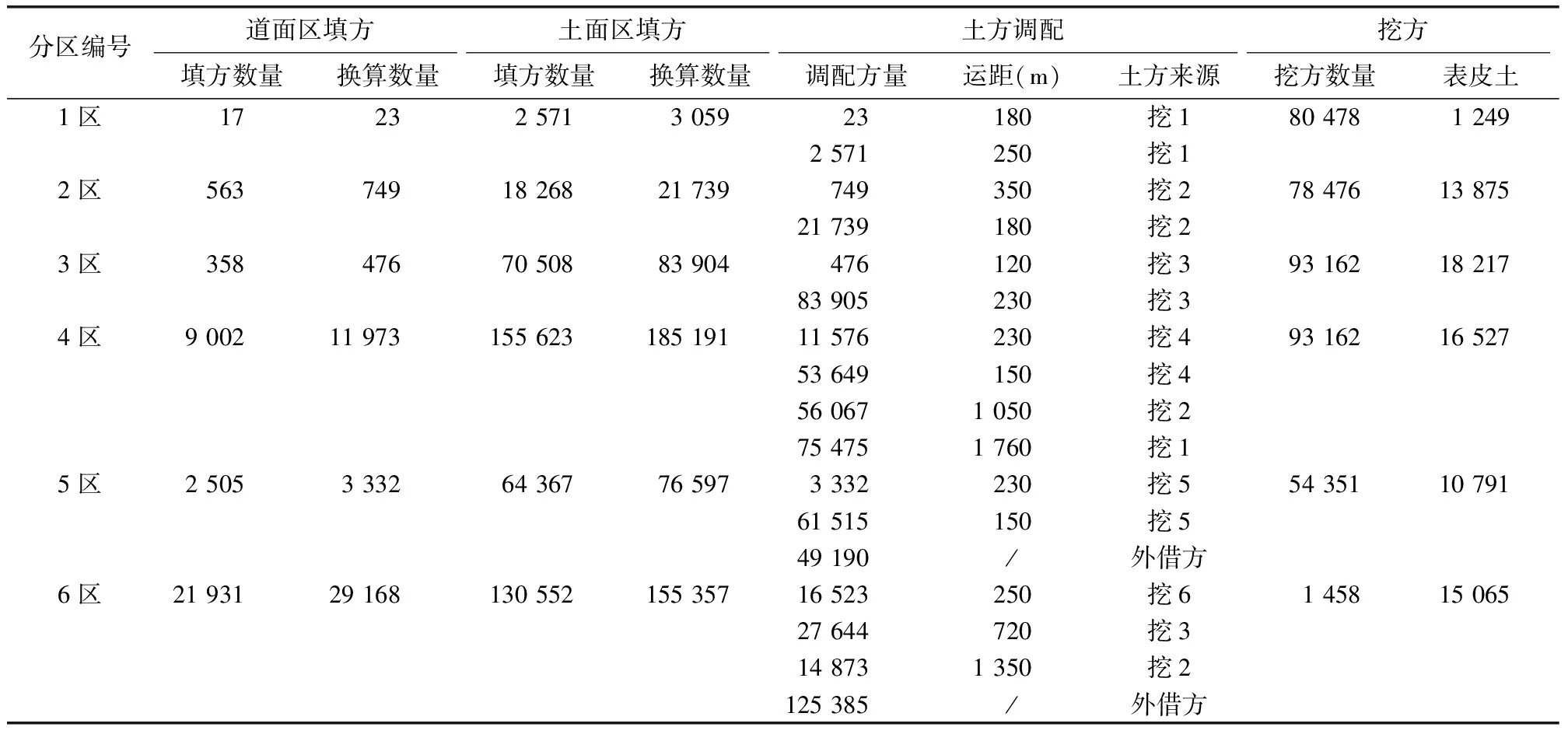
表4 全场土石方调配工程数量

3.4 调配方案与设计方案的比对和分析

设计方案是根据场地形状将场地划分为6个大区，每区内分为挖方区、土面区填方、道面区填方，挖方区又根据挖方土的性质分为表皮土和非表皮土。在6个土方分区的前提下，坚持全局最优、土方调配量和运距乘积最小的原则，制定了全场土石方调配方案，全场土石方及调配工程数量表如表4所示。传统方法仍然是手工或者利用二维图纸计算土方量再进行土方调配，而基于三维实景和BIM模型比对获取土方量能够更加精准也更加适用于准确测算土方量，并在此基础上进行土方调配。

在全局最优的前提下，调配方案是将场地根据场地形状、结构形式划分为13个分区，相比于设计方案而言，土方分区划分更加细致准确，因此在此基础上进行线性规划模型计算得到的调配方案更加合理，解也更优。

4 结语

本文介绍了一种基于三维实景模型与BIM模型比对获取土方量，进而进行土方工程分区调配的方法。利用该方法获取土方量减少了现场测量和人工计算工作，综合考虑了场地实际情况，并且大幅度提高了土方计算精确度。在此基础上建立线性规划数学模型，在全局最优的原则下尽可能满足挖填方平衡，以土方量与运距乘积之和最小为目标函数，求解得到比依据项目经理实际经验更优的土方调配方案，在某一机场项目中进行了实例验证，用以指导施工，降低土方运输成本。