基于时间序列的纱线直径预测方法

2021-02-10王延蒙

纺织器材 2021年6期

王延蒙

(济宁职业技术学院，山东济宁 272073)

0 引言

纱线质量常用的表征参数为条干不匀率，而纱线直径是计算纱线条干不匀的主要参数[1-2]。神经网络模型广泛应用于预测纱线质量：王侃枫等基于遗传规划的基本原理，建立纱线条干不匀率的非线性关系函数模型[3]；张羽彤等使用优选方法，选取4种对纱线条干不匀率影响最大的参数，并基于BP神经网络预测纱线质量[4]；王东平等基于关联度分析原理，建立支持向量机回归的纱线质量预测模型，在小样本容量下的拟合性好于BP神经网络[5]；杨建国等改进ELM算法，使用精梳工序的10个工艺指标作为输入参数，建立毛纱条干值的预测模型[6]；袁利华通过使用HVI检测系统选取输入层变量，建立基于RBF神经网络的纱线条干不匀预测模型[7]。

上述预测模型的预测结果经过与实际值对比，取得了较好的预测效果，但均是基于加工纱线工序的各项工艺参数进行预测。时间序列预测是基于对历史数据的分析，预测未来数据的变化情况。笔者提出一种基于时间序列预测纱线直径的模型，根据线阵CCD测量的纱线直径，建立比较精确的、反映纱线直径预测值和历史值关系的数学模型。

1 时间序列预测方法

使用线阵CCD对纱线直径在线实时测量，在相等间隔的时间段内测量的纱线直径值构成纱线直径的时间序列。时间序列预测方法，主要包括自回归模型(AR模型)、移动平均模型(MA模型)和自回归滑动平均模型ARMA(p，q)预测方法[8-9]。

纱线直径自回归模型预测的基本思想，是利用前期测量的纱线直径的线性组合来描述之后某时刻的纱线直径。纱线直径移动平均模型基本思想，是取相同时间间隔对纱线直径时间序列的数据计算其滑动平均值。自回归滑动平均模型为自回归与移动平均的结合。纱线直径的预测值不仅与先前相等间隔时间段的直径值存在关系，而且与先前时刻的噪声干扰存在关系。纱线样本时间序列如图1所示，

图1 纱线样本时间序列

可将ARMA(p，q)时间序列表示为：

(1)

式中：xi为当前值，p为自回归系数，q为滑动平均系数，φi为自相关系数，xt-i为前一项值，at为平稳白噪声，θi为消除随机波动的参数，at-i为误差参数。

2 预测步骤

选取100个纱线直径测量点，其中90例用于时间序列建模，10例用于预测验证。

2.1 单位根检验平稳性

时间序列处理的数据要求能够满足平稳性。采用ADF单位根检验的方法，验证纱线直径时间序列是否平稳。ADF单位根检验过程：首先假设纱线直径时间序列为非平稳序列，则序列存在单位根，计算该时间序列的统计值，如果得到的统计量值显著小于3个置信度(1%，5%，10%)的临界值且假定值接近于0，说明原假设不成立，则判定该时间序列为平稳时间序列。结果如表1所示，表明所处理的纱线直径时间序列为平稳序列。

表1 ADF检验结果

2.2 阶数选择

自相关函数(ACF)指任意时间t的序列值xt与其自身的滞后值xt-1，xt-2，xt-3，…，xt-i之间的线性关系。它描述了纱线直径时间序列的当前纱线直径值，与其过去直径值之间的相关程度。自相关函数反映了xt与其自身的滞后值xt-i的相关关系。

偏自相关函数(PACF)是指残差与下一个滞后值的相关性。因此，如果残差中有任何的下一个预测纱线样本直径建模的隐藏信息，则残差与时间序列预测值具有良好的相关性。

根据自相关函数ACF和偏自相关函数PACF确定ARMA(p，q)模型的参数p和q。采用的方法是计算时间序列的20阶自相关系数和偏自相关系数，阶数选择时依据原则如表2所示。截尾的含义是在自相关函数图中某阶之后系数趋于0，拖尾的含义是在偏自相关函数图表现为衰减的趋势。

表2 定阶原则

图2和图3分别为样本数据的自相关函数图和偏自相关函数图。从图2可以看出自相关系数3阶拖尾，从图3看出偏自相关系数2阶拖尾，因此初步确定为ARMA(3，2)模型。

图2 纱线样本数据的自相关函数示意

图3 纱线样本数据的偏自相关函数示意

2.3 模型优选

AIC信息准则是一种常用的、衡量统计模型优良性的标准，可以评估所建立时间序列模型的复杂度和模型对历史数据拟合的准确度[10]。模型优选的目标是选取AIC最小的模型，分别通过MAT-LAB计算ARMA(0，0)，ARMA(0，1)，ARMA(1，0)，ARMA(1，1)，ARMA(1，2)，ARMA(2，1)，ARMA(2，2)，ARMA(2，3)，ARMA(3，0)，ARMA(3，1)，ARMA(3，2)模型的AIC值，确定最优预测模型为ARMA(3，2)。

2.4 残差检验

为确保时间序列模型的预测效果，需要对模型ARMA(3，2)进行残差的正态性检验[11]。残差是线阵CCD实际测量的直径值与时间序列模型估计值的差，残差分布应符合正态分布。使用Quantile-Quantile图，比较纱线样本残差数据的分位数与正态的分位数，从而检验残差数据的分布情况。其中，理论分位数数据集对应x轴，样本分位数数据集对应y轴。图4为纱线直径的Quantile-Quantile图，图上的点近似地呈直线分布，说明是正态分布，残差符合正态性检验。

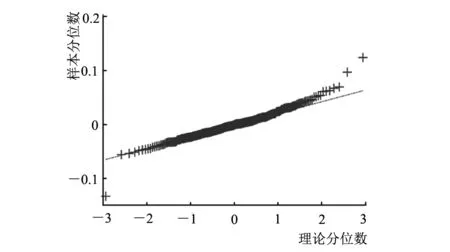
图4 纱线直径Quantile-Quantile图示意

3 实验结果分析

对纱线样本时间序列分别使用自回归模型、移动平均预测模型进行预测，预测结果如表3所示。

表3 纱线样本预测精度对比

由表3可知：① 使用相同数量的纱线样本直径建立预测模型，预测相同数目的纱线直径进行比较，ARMA模型的预测误差小于5%和10%的比例最高；② 使用不同数量的纱线直径点进行建模，预测不同的数据个数，当参加建模的纱线样本数量增多，预测数据同样增加时，AR和MA预测的准确度无明显增加，而ARMA模型预测准确度得到明显提高。实验结果表明，ARMA模型的预测精度较高，可用于纱线直径在线检测过程中的纱线直径预测。