IDC 机柜结构地震工况非线性时程分析研究*

冯 卉，杜文嫚，张朋波

（1. 中兴通讯股份有限公司，江苏南京210000；2. 信通院（保定）科技创新研究院，河北保定071000）

引 言

中国已进入大数据时代，巨大的数据价值势必对互联网数据中心（Internet Data Center, IDC）机房设备的抗震性能和可靠性提出更高的要求。机柜是IDC 机房的一个重要组成部分，其作用是方便安装和固定服务器等IT 设备。当前对IDC 机柜的承载能力要求高，但在高承载工况下，IDC 机柜缺少相应的抗震设计，抗震性能差，设备倾倒、结构开裂、门板打开和连接失效等问题突出。

目前振动仿真分析技术通常采用线性振动理论和仿真分析模块，无法正确模拟接触这样的典型非线性问题，导致仿真与实际误差较大，无法真正指导设计。非线性振动技术是解决恢复力与位移不成线性比例关系或阻尼力与速度不成线性比例关系的振动问题的技术。

为了较为准确地解决地震载荷作用下IDC 机柜结构产生的大变形和高应力问题，本文以IDC 机柜为研究对象，采用Radioss 求解器进行非线性时程计算，并且进行物理样机的抗震试验，在与试验数据对比的基础上不断修正分析模型，研究IDC 机柜模型的动力响应。

1 非线性时程分析

显示时程分析法通常采用中心差分法。中心差分法用有限差分代替位移对时间求导（即速度和加速度）。如果采用等时间步长，则速度˙u 和加速度¨u 的中心差分近似为：

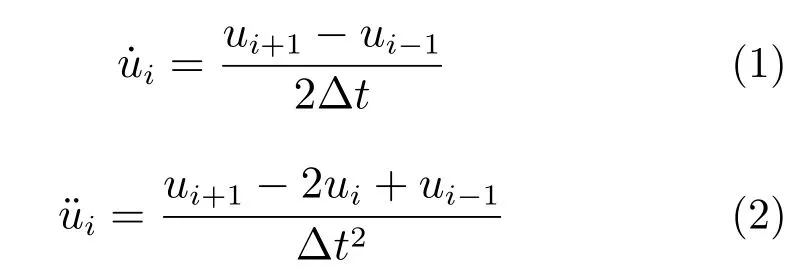
而离散时间点的运动为：

ui=u(ti), ˙ui= ˙u(ti), ¨ui= ¨u(ti), (i=0,1,2,···)

体系的运动方程为：

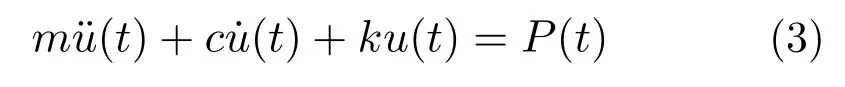
式中：m,c,k 为系数；u 为位移；t 为时间；P 为系统受到的外力。

将速度和加速度的差分近似公式（1）和（2）带入由式（3）给出的ti时刻的运动方程可以得到：

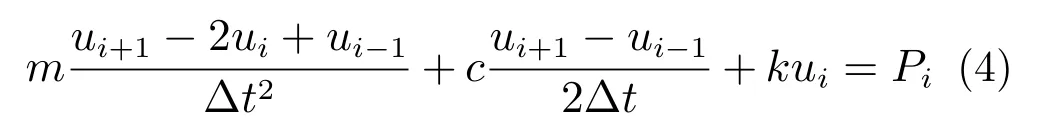
在式（4）中，假设ui和ui−1已知，即ti时刻及以前的运动已知，则可以整理方程得到：

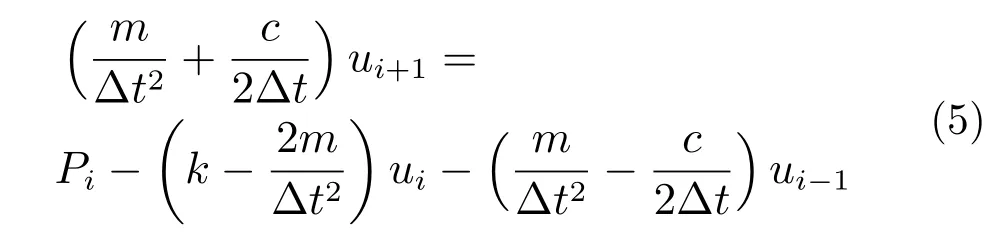
由式（5）就可以根据ti时刻及以前的运动求得ti+1时刻的运动。式（5）即为结构动力反应分析的中心差分法逐步计算公式。

2 地震波处理

本文地震波选取依照YD 5083—2005《电信设备抗地震性能检测规范》中8 烈度、非电源类设备规定，由楼面反应谱根据随机相位法生成人工合成地震波，地震加速度峰值为0.66g（g =9 800 mm/s2），持续时间为30 s，强震部分持续20 s。计算加载前，对地震波加速度数据进行基线校准和高通滤波，避免加速度信号通过积分求速度、位移时，原始基线漂移逐步放大，导致分析结果出现基线漂移。处理后的地震波加速度、速度和位移信号见图1。

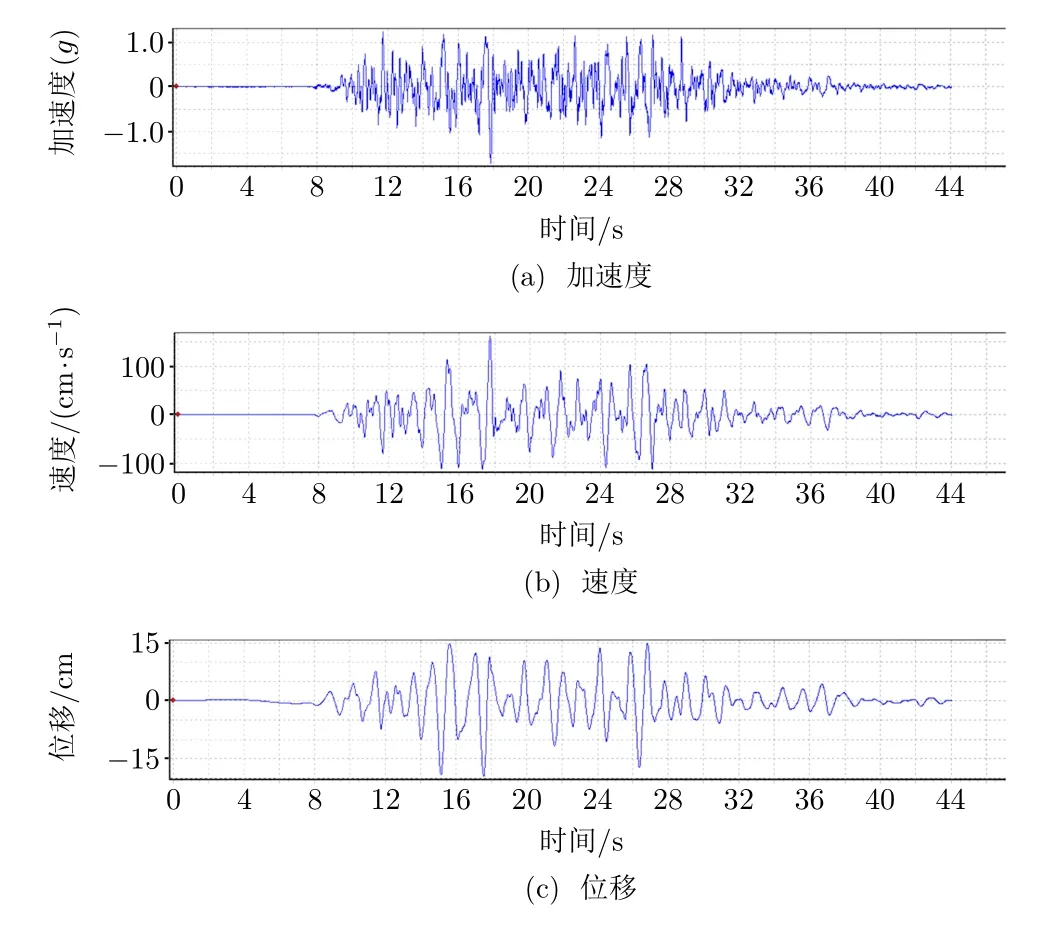
图1 8 烈度、非电源类设备地震波加速度、速度和位移曲线

3 有限元建模

3.1 材料模型

本文采用最经典的弹塑性动力学材料模型——Johnson-Cook 材料模型。在此材料模型中，材料达到塑性之前，其真实应力按杨氏模量计算，达到塑性之后，材料的真实应力表达为塑性应变、应变率和温度的函数，即：

式中：σ 为真实应力；εp为塑性应变；a 为屈服强度；b 为硬化模量；n 为硬化指数；c 为系数；ε 为参考应变；ε0为试验应变；T 为温度；m 为热软化指数。

本文工况忽略第2 部分应变率和第3 部分温度变化的影响。第1 部分参数a，b，n 的确定过程为：在软件中提供材料屈服应力σy，最大拉伸应力σUTS（由工程应力-工程应变曲线得到）和其对应的工程应变εUTS3 个参数，自动求解计算。

取机柜托盘结构作为拉伸试验件，进行3 次拉伸试验，得到3 条材料拉伸工程应力-应变曲线。取σy，σUTS和εUTS的平均值225 MPa，321 MPa 和0.2 进行分析。

3.2 材料失效本构

采用Radioss 材料本构中自带的失效模式进行分析，需设置最大应力及材料断裂时的应变。将3 条工程应力-应变曲线换算成真实应力-应变曲线，取值从真实应力-应变曲线得到，见表1。

表1 软件设置冷轧钢板材料参数

3.3 单元类型、网格尺寸与网格质量

在Hyper Mesh 中构建IDC 机柜抗震时程分析有限元模型，如图2 所示。机柜主框架、内立柱、托盘等结构以平均单元尺寸8 mm 进行剖分，均采用二维单元P1-SHELL 进行离散。连接螺栓和焊接采用Rigid 单元模拟，在托盘与配重块之间存在潜在接触部位，采用Radioss Type7 接触模型建立接触对，并考虑摩擦影响。网格剖分共获得223 574 个单元。三角形单元过于刚硬，模型中三角形单元的占比为0.05%，满足精度要求。在边缘处或有孔的结构中，任何方向上都至少有三层单元。

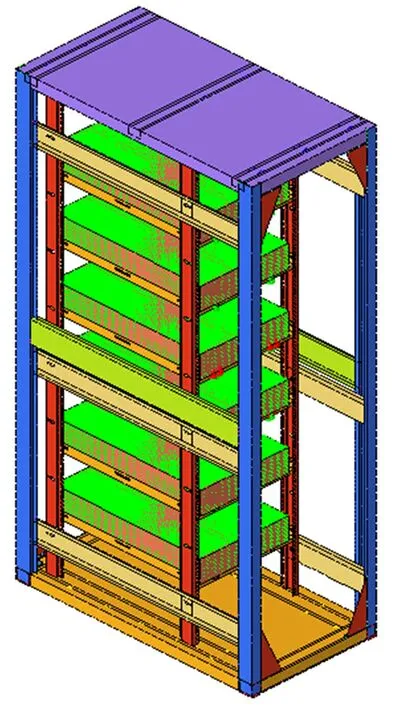
图2 IDC 机柜有限元模型

3.4 沙漏能控制

显示分析中采用缩减积分会造成沙漏能。缩减积分是指单元计算时积分点数少于实际个数，这种操作能加快计算速度，但是会造成一种单元的零能模式，这就是沙漏。计算要求沙漏能的占比在−15%～−10%之间。分析时，通过沙漏粘性阻尼算法进行控制，即施加一个与沙漏模态变形方向相反的沙漏阻尼力来抵御变形。分析模型的内能、沙漏能和总能曲线见图3。沙漏能的最大占比为−3%，能保证计算结果稳定、准确。

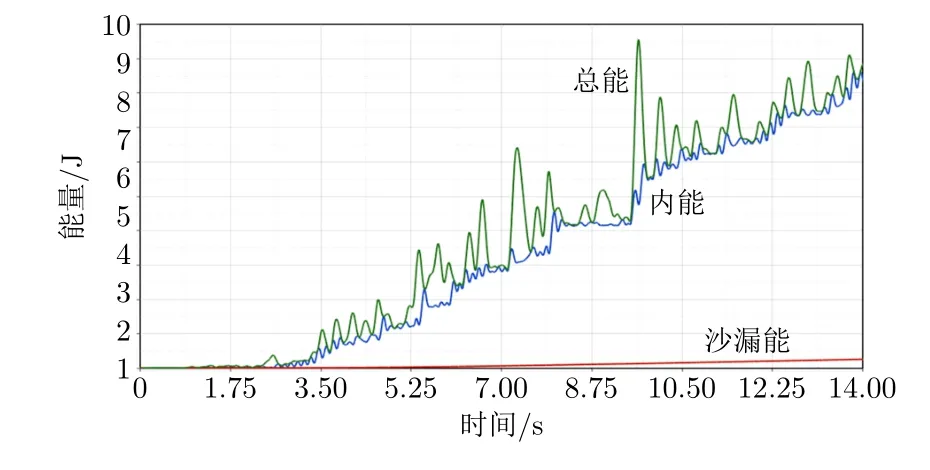
图3 有限元模型内能、沙漏能和总能曲线

4 结果对比

4.1 评价指标

本文以地震试验得到的位移数据为基准，以峰值和峭度2 个参数为评价指标，对试验数据和分析数据进行对比，评价分析结果的准确性。

峰值是指信号时域图中某一时刻的振幅最大值。峭度是反映随机变量分布特性的数值统计量，是归一化的4 阶中心距，可以表示波形平缓程度，用于描述变量的分布。

4.2 仿真与试验结果对比

4.2.1 变形现象对比

8 烈度地震载荷作用下最大位移时刻的变形结果的仿真与测试对比如图4 所示。结构变形的仿真分析和试验现象一致。

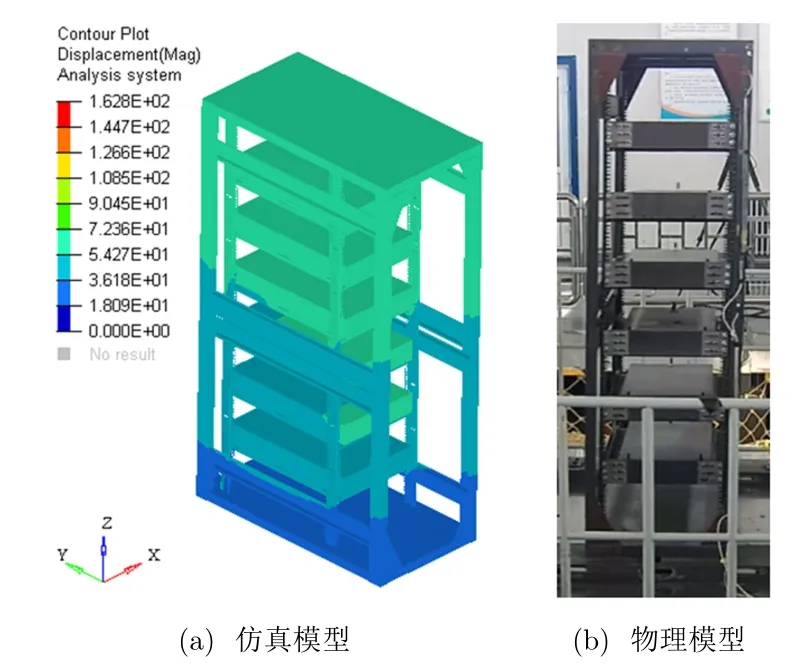
图4 仿真和测试对比

4.2.2 位移峰值对比

读取8 烈度工况下结构地震试验位移和仿真分析位移数据，绘制曲线，如图5 和图6 所示。试验位移峰值为37.8 mm，仿真分析位移峰值为33 mm，两者相差12.7%。

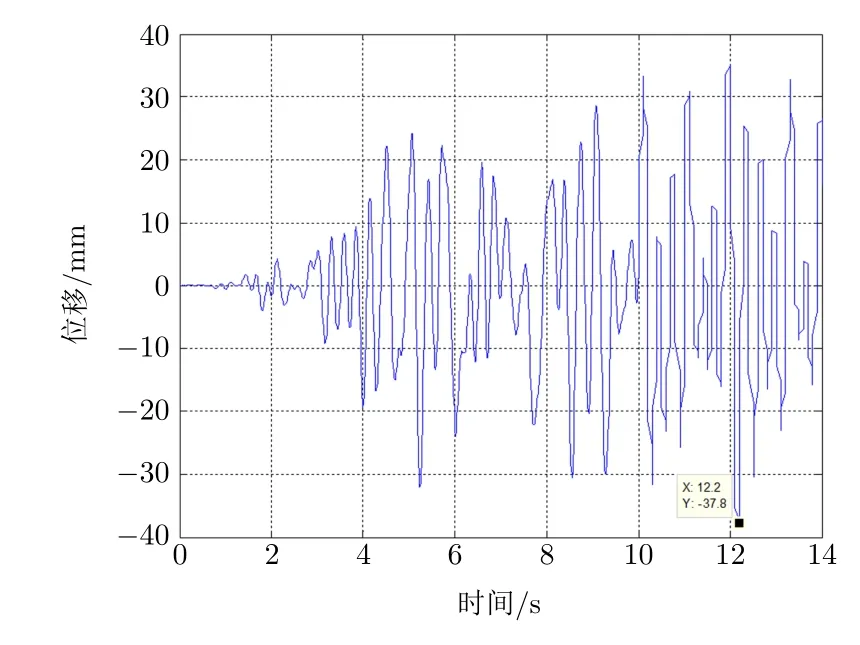
图5 试验位移曲线

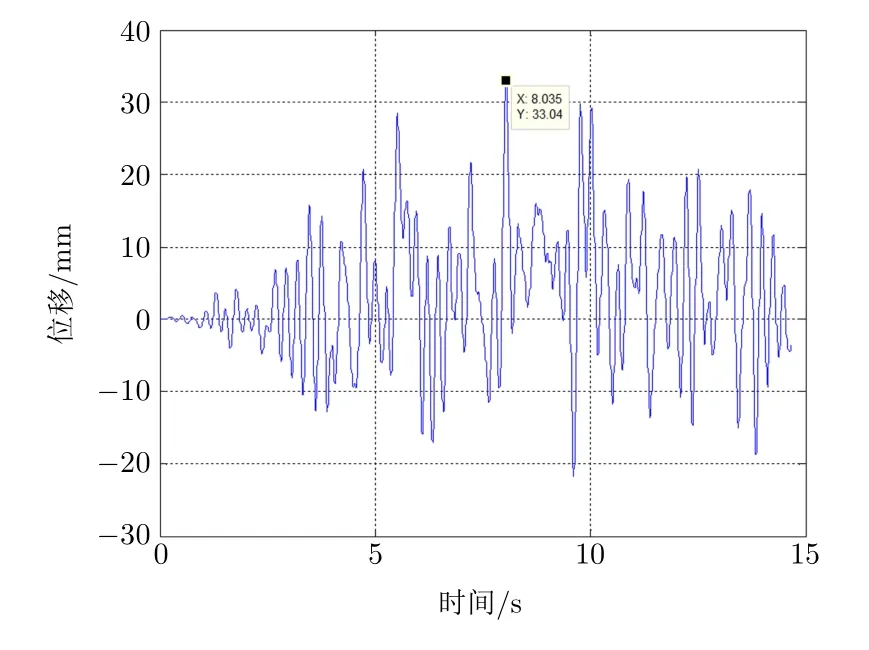
图6 仿真分析位移曲线

4.2.3 峭度对比

分别对试验数据和仿真分析数据进行峭度值计算，试验峭度值为3.23，仿真分析峭度值为3.45。峭度指标值约为3，振动信号接近正态分布，试验和仿真的信号分布一致，无较大的冲击信号出现。

5 结束语

从IDC 机柜抗震仿真分析结果来看，仿真分析机柜变形趋势接近机柜实际物理试验状态。

从试验位移曲线和仿真分析位移曲线结果来看，两条曲线的波形、趋势、峰值和峭度基本吻合，表明IDC 机柜采用非线性时程分析方法可以准确模拟机柜在地震过程中的动力响应。

在IDC机柜抗震仿真与物理试验对标研究中，网格尺寸、网格质量、材料模型、接触和沙漏能控制是仿真结果与物理试验对标的关键。通过有限元建模细节的控制，可使仿真分析结果接近试验结果。

本文建立的非线性时程分析方法合理、准确，可有效模拟地震作用下结构的受力和真实状态，在机柜抗震设计过程中可实现仿真驱动设计。同时，建模方法可以推广到其他通信设备的非线性时程分析中。