一道经典高考试题的多解赏析及追问

王胜华 陈向正

(重庆市清华中学 重庆 400054)

高中物理教学中常见这样一类匀强电场的典型问题：假设匀强电场的电场线与某平面共面，已知该平面上3个点的电势数值，求解场强的大小和方向.近几年这种类型的问题在高考试题中多次出现.

1 试题

如图1所示，在平面直角坐标系中，有方向平行于坐标平面的匀强电场，其中坐标原点O处的电势为0 V，点A处的电势为6 V，点B处的电势为3 V，则电场强度的大小为多少？

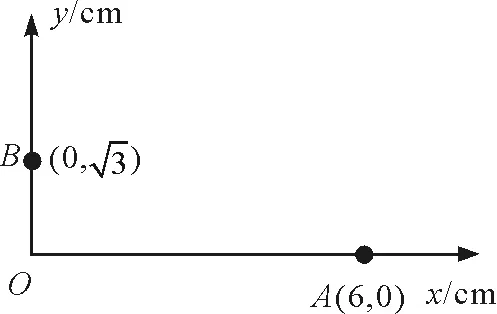
图1 试题题图

2 求解

2.1 平面几何法

平面几何法的一般步骤是先在两个已知电势点的连线上找到第三个点的等势点，作这个点与第三个点的连线即为等势线，再作等势线的垂线确定电场线，最后根据电场强度的大小与电势差的关系U=Ed来求解电场强度的大小.这种方法最常见.

解析：如图2所示，取O和A的中点C，则C点的电势为3 V，则C和B两点电势相等，连接CB，根据匀强电场的等势线为直线的性质，则CB为等势线，电场线和等势线垂直且指向电势降低的方向，过O点做CB的垂线交CB于D点，则DO为电场线，由几何知识可知DO的距离d=0.015 m，而φD=φC=φB=3 V，φO=0 V，所以

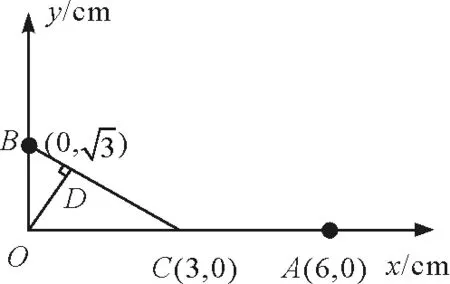
图2 平面几何法求电场强度

则电场强度

电场强度方向沿DO方向，与x轴负方向夹角正切

2.2 正交分解法

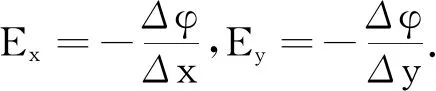
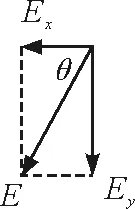
图3 正交分解法 求电场强度

故正交分解法的一般步骤是先分别算出电场强度在两垂直的坐标轴方向的Ex，Ey，然后再用合成法求出电场强度E,如图3所示.

则有

可得

电场强度方向如图3,电场强度方向与x轴负方向的夹角正切

2.3 空间向量法

在高中数学中，由空间向量基本定理可知，对于空间任意一个向量p，在直角坐标下，可记作p=(x,y,z)，即为“向量的坐标表示”，对学生而言是非常熟悉的[1].那么,对于某平面内的电场强度矢量可以采用向量的坐标表示法，将E表示为E=Exi+Eyj=(Ex,Ey)，将L表示为L=xi+yj=(x,y)，因电势差与电场强度的关系可以写成|Δφ|=E•L，即

|Δφ|=(Ex,Ey)•(x,y)=xEx+yEy

则有

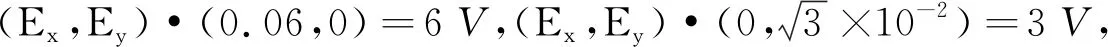
电场强度方向与x轴负方向的夹角正切

3 追问

从理论上讲，平面几何法在任何情况下都可以求解这类问题，但从求解过程可以看出，所幸题设给的数据特殊，便于计算求解.若把A点坐标改为(10，0)，则求解的过程有很大的难度，计算量大，不具备可操作性.

对于正交分解法，从求解过程可以看出，正交分解法方法简洁，思路简明，但若把例题中A点坐标改为(10，1)，由于OA与OB不再垂直，利用正交分解法求解将有很大的难度.用空间向量法可以解决.

空间向量法在求解电场强度时与在高中数学中利用空间向量法求解立体几何问题在原理和方法上是一致的.因此，学生很容易理解且能够快速熟练掌握.此外，空间向量法还适用于上面两种方法不方便求解的三维空间匀强电场中求电场强度的问题.若把例题中A点坐标改为(10，1)，只有空间向量法能够快速求解.

即有

则有

(Ex,Ey)•(0.1，0.01)=6 V

(1)

(2)

为详细说明求解方法，下面分步计算.

由式(1)得

(Ex,Ey)•(0.1,0.01)=0.1Ex+0.01Ey=6 V

(3)

由式(2)得

(4)

式(4)代入式(3)得

电场强度方向与x轴负方向的夹角正切

【例1】如图4所示，边长为2 m的立方体空间存在匀强电场，其中a，b，c，d点的电势分别为1 V，11 V，5 V，8 V，求电场强度的大小？

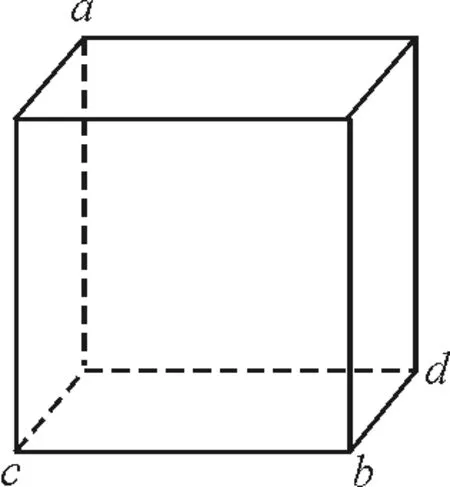
图4 例1题图

解析：以c点为坐标原点，建立三维直角坐标系，如图5所示，则有a，b，c，d4点的坐标分别为(0,2,2)、(2,0,0)、(0,0,0)、(2,2,0).

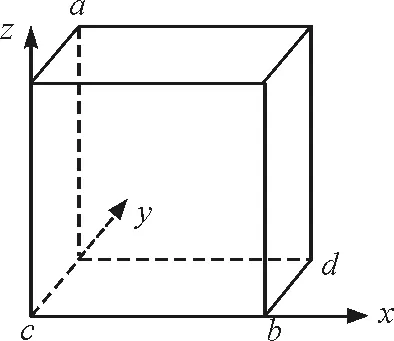
图5 以c为原点，建立三维直角坐标系

则有ca=(0,2,2),cb=(2,0,0)，cd=(2,2,0)，有

Uca=E•ca=(Ex,Ey,Ez)•(0，2,2)=4 V

即

2Ey+2Ez=4 V/m

Ucb=E•cb=(Ex,Ey,Ez)•(2，0,0)=-6 V

即

2Ex=-6 V/m

Ucd=E•cd=(Ex,Ey,Ez)•(2，2,0)=-3 V

即

2Ex+2Ey=-3 V/m

可得

空间向量法是一种学生容易理解且在高中数学中常用的方法，可快捷求解匀强电场的电场强度.这种方法有利于增强学生学科融合意识，拓展学生视野，提升学生思维能力.教师们在教学中不防一试.