多粒度时空事件序列相似度算法研究
2021-02-07汪成亮黄利莹赵凯
汪成亮, 黄利莹, 赵凯
(重庆大学 计算机学院,重庆 400044)
随着无线通信技术、嵌入式技术等技术的不断发展,智能环境也进入了飞速发展阶段,它在环境监测、智能家居、医疗护理等方面[1-3]得到了广泛的应用. 智能环境下经过处理可以得到用户大量的日常活动事件序列数据,包括活动类型、活动开始时间与结束时间、位置信息等,对这些事件序列进行相似度度量,可以聚类分析出行为相似的用户、进行用户行为异常检测、查询与给定序列相似的其他行为序列等,将其与健康医疗或智能推荐等领域[4-7]相结合,为用户提供个性化信息服务,用以改善用户的日常生活.
当前,关于用户行为分析的研究之一就是用户行为相似度计算,主要集中于不带有时间空间信息或带有固定时间空间信息的活动序列相似度计算,本文认为仅仅从单一层次来计算时空事件序列相似度是不够的,难以准确地进行相似度度量. 例如,如图1所示,利用现有的活动序列相似度计算方法,事件序列1与事件序列2显然相似性不高,但若放大空间层次和活动层次,如图2所示,则事件序列1与事件序列2的相似性明显高于图1所示. 因此,需要从不同的粒度对时空事件序列进行相似度比较.
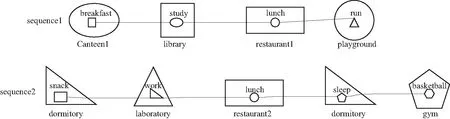
图1 事件序列相似性比较Fig.1 Similarity comparison of event sequences
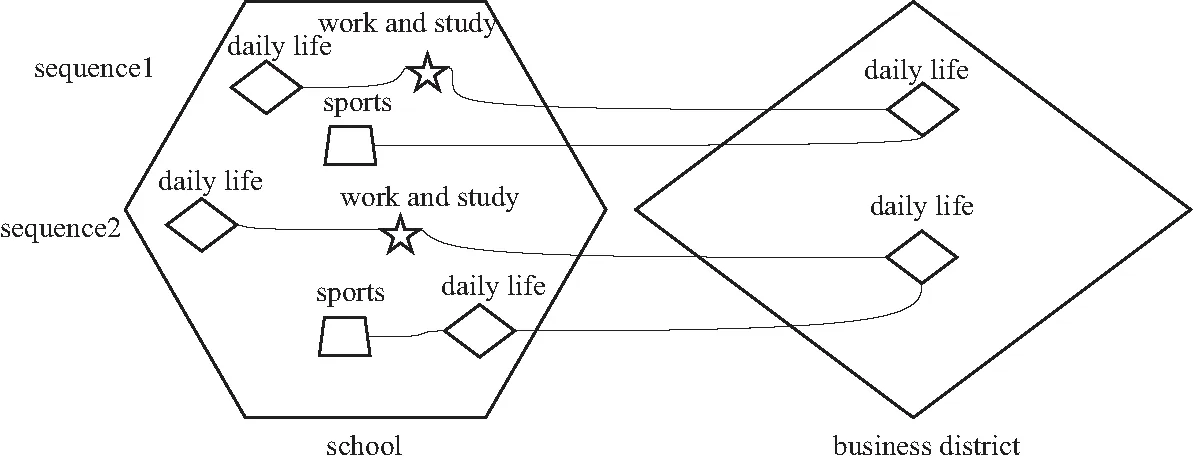
图2 调整空间和活动层次后的事件序列相似性比较Fig.2 Similarity comparison of event sequences after adjusting spatial and activity levels
与本文相关的工作主要是事件序列相似度计算方面. 关于事件序列的相似性度量,目前已经有了一定的研究成果. Banerjee等[8]把两序列的交叉程度作为其相似性的度量标准, 采用两个序列的最大共同子序列LCS表示序列的距离;Mannila等[9]用编辑距离表示两序列的相似度,其基本思想是:两序列的相似性反映为把一个序列转换成另一序列的工作量. 然而以上方法仅处理纯粹的定性信息,如字母,而不能处理带有时间、空间信息的序列. Ying等[10]提出语义轨迹模式相似度方法来度量两个轨迹之间的相似性,该方法将轨迹转化为具有语义标签的位置序列,通过最长公共子序列计算两个序列的相似度,但该方法忽略了时间、活动信息,仅考虑空间相似度;Sajimon Abraham等[11]提出时空相似度算法TraSimilar来度量用户轨迹相似度,该方法将原始轨迹数据中的空间信息视为一组序列,利用序列比对方法测量轨迹之间的空间相似度,然后再求两条轨迹中对应相同空间位置的时间距离,将时间相似度定义为时间距离的倒数;Yuan等[12]提出了时空编辑距离方法来衡量用户轨迹之间的相似度,该方法扩展了传统编辑距离算法的成本函数,以便结合空间和时间因素. 以上方法比较的是带有固定时间空间信息轨迹之间的时空相似度,忽略了时间、空间信息的多尺度表达,且没有考虑活动之间的相似度.
NW算法[13]广泛应用于序列比对,但该算法仅是对字符之间的简单比较,无法准确高效地对时空事件序列进行相似性比较,因此,本文对NW算法进行了改进,提出了多粒度时空序列比对算法MGSSA,实现了从不同的层次计算时空序列相似度,最后理论分析和实验验证表明了该算法的有效性. 与NW算法相比,本文提出的MGSSA算法在一般情况下,度量时空事件序列相似度的效率和语义完整性均优于NW算法.
1 相关概念
1.1 时空事件、时空事件序列
给定活动类型集合E={e1,e2,…,en},n为活动类型总数,时空事件表示为一个三元组event=(t,e,p),其中,t=(tstart,tend),tstart为事件的开始时间,tend为事件的结束时间;e为活动类型集E中的某个事件;p为事件发生时用户所在的位置. 时空事件具有多粒度的特性. 时空事件序列表示为L={event1,event2,…,eventn},其中n为时空事件序列中事件的总数.
1.2 粒度
时空事件具有多粒度[14]的特性,下面分别对活动粒度、空间粒度、时间粒度进行定义.
定义1活动粒度:在智能环境下,对通过传感器检测或识别到的活动进行多层次的分类(如图3所示),则每一层次称为一个活动粒度,一个活动粒度表示为AG(i)(i表示活动粒度的个数).

图3 活动粒度Fig.3 Activity granularity
定义2空间粒度:设R为智能环境区域(如图4所示),在R内有n个互不相交的子区域p(i)⊆R(1≤i≤n)且p(i)∩p(j)=∅(1≤i,j≤n),p(i)被称为是一个空间粒,则所有p(i)(1≤i≤n)空间粒构成的即为一个空间粒度,一个空间粒度表示为SG(i)(i表示空间粒的个数). 图4中,智能环境区域经过一次划分所得的子区域p(1)~p(4)各为一个空间粒,所有的p(i)空间粒构成一个空间粒度,每个子区域p(i)再次进行划分得到子区域p(i1)~p(i4),所有的p(in)空间粒构成另一个空间粒度,依此类推到其他各空间粒度.

图4 空间粒度Fig.4 Spatial granularity
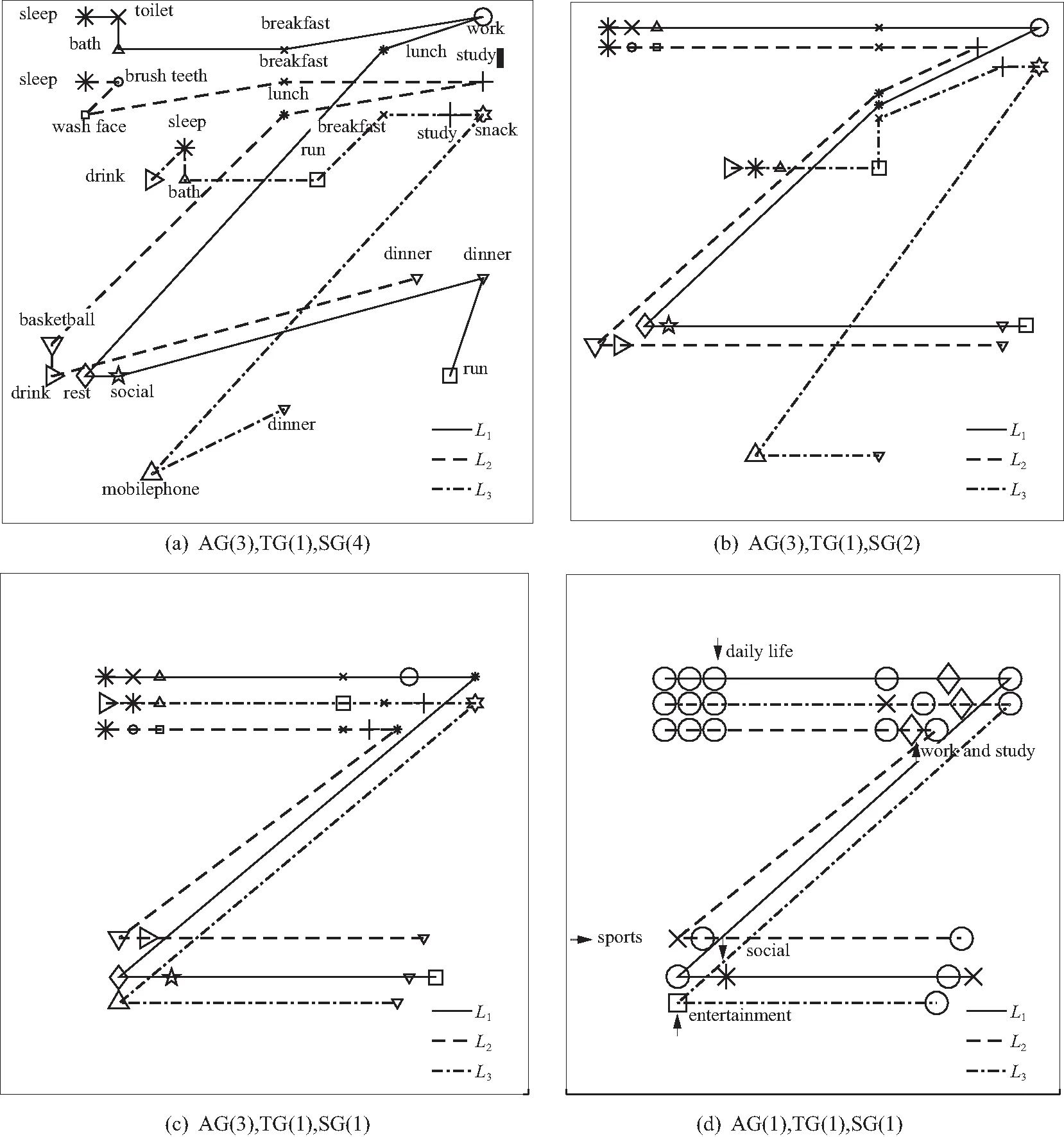
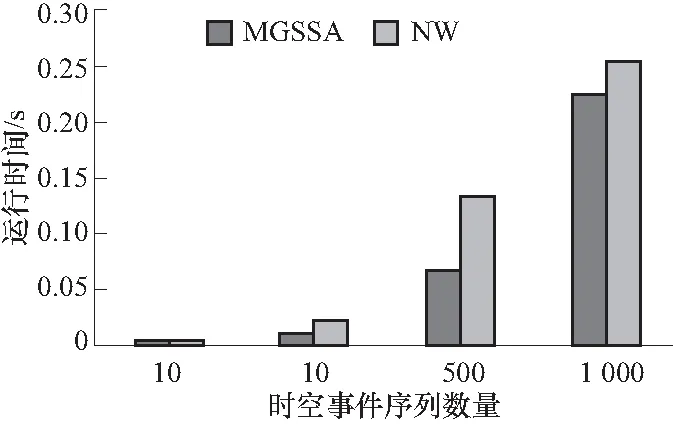
定义3时间粒度:设T=[t0,tn]是时间域,T内有n个互不相交且时间间隔相同的时间区间:t(i)=[ti1,ti2],t(j)=[tj1,tj2],(t0≤ti1 图5 时间粒度Fig.5 Temporal granularity 传统的序列挖掘中的事件很多都是瞬时事件,这样事件的发生关系很简单. 而对于带有时间间隔的事件来说,因为每个事件都有两个时间点,事件间的关系就要复杂得多,下面就对时间间隔事件间的关系表达[15]做详细的介绍. 对于两个事件event1、event2的关系来说,本文定义以下几种关系模式,在定义中默认为event1在event2之前发生,即tstart(event1)≤tstart(event2). ①NoOverlap(event1,event2):表示事件event2在event1结束时或结束之后发生,即tend(event1)≤tstart(event2). ②Overlap(event1,event2):表示事件event1与事件event2发生的时间上有重叠,即tstart(event1)≤tstart(event2),tend(event1)>tstart(event2)且tend(event1) ③Contain(event1,event2):表示事件event1包含事件event2,即tstart(event1)≤tstart(event2),tend(event1)>tend(event2)或tstart(event1) ④Equal(event1,event2):表示事件event1与event2同时发生并且同时结束,即tstart(event1)=tstart(event2)且tend(event1)=tend(event2). 但是在现实生活中事件发生的时间并非十分精确,如有的开始结束时间可能精确到小时,有的可能精确到分、秒. 这样就使事件界限的定义模糊不清,也使得事件间的关系定义模糊不清. 于是,本文接着通过加入时间限制方法,将上述定义的4种关系模式转化为下面所示的4种关系,可以看出,关系定义的基本概念是相同的,只是加入了一个时间限制值,当时间差超过这一限制时,两个事件之间的关系才成立. 给定一个阈值th(th>0),th对于不同的关系定义是不同的. 那么上述4种关系可以重新定义如下: ①NoOverlap(event1,event2):tstart(event2)-th≤tend(event1)≤tstart(event2)+th或tend(event1)+th≤tstart(event2). 说明:在一些情况下,如果两个事件的间隔时间太长,那么这个“NoOverlap”关系是没有意义的,所以设置一个最大时间差tmax,当tstart(event2)-tend(event1)>tmax时,两个事件“NoOverlap”关系不成立,即两个事件没有任何关系. ②Overlap(event1,event2):tstart(event1)+th≤tstart(event2),tend(event1)+th≤tend(event2). ③Contain(event1,event2):tstart(event1)+th≤tstart(event2),tend(event1)≥tend(event2)+th或tstart(event1)+th ④Equal(event1,event2):tstart(event2)-th≤tstart(event1)≤tstart(event2)+th且tend(event2)-th≤tend(event1)≤tend(event2)+th. NW算法是基于动态规划的全局最优比对算法,能够找出序列的最优比对并计算其最大相似性. 序列之间字符可能匹配、不匹配或匹配gap(由插入或删除操作产生),NW算法定义了一个字符得分系统,可以针对不同的情况设计不同的得分系统,设字符x与y进行比较时的得分函数W(x,y)为 (1) NW算法将两个序列a,b变成等长序列,不等长则用gap补足,形成一个二维矩阵,矩阵的单元是计算得出的对应子序列的相似度值. 用S(i,j)表示矩阵单元的值,则序列a和序列b的全局最优比对可表示为 S(i,j)= (2) 根据式(2)可以计算出矩阵中每个单元格的分数,最后即可得到完整的序列比对后的相似度矩阵. 矩阵右下角的相似度值最大,从矩阵右下角回溯至左上角,即可得到序列最优比对的结果. 本文提出了一种基于NW算法的多粒度时空序列比对算法(multi-granularspatiotemporalsequencesalignment,MGSSA),通过将空间和时间信息结合到得分函数中来改进传统的NW算法. 并能通过粒度调控来从不同粒度对时空序列进行相似性比较. 算法NW是从序列第一个到最后一个,一个一个进行比较,一条序列比个遍,然后得出最优解,仅仅是对两个字符串的最优比较. 然而,对于此问题,即计算两个时空事件序列的相似度,而不是序列的最优比较得分,且时空事件序列不仅包含活动信息,还包含时间、空间信息,所以基于NW算法的得分函数,提出了时空事件相似度计算公式如下. 定义4时空事件相似度:eventi=(ti,ei,pi)和eventj=(tj,ej,pj)是时空事件序列L中的两个时空事件,那么eventi和eventj的相似度计算公式如下: w(eventi,eventj)= (3) 式中:Sactivity表示两个事件eventi,eventj比较的活动相似度;Stime表示两个事件eventi,eventj比较的时间相似度;Sspace表示两个事件eventi,eventj比较的空间相似度;u1、u2、u3分别为Sactivity、Stime、Sspace对应的相似度权重,用来调整对活动相似度、时间相似度、空间相似度的敏感度,且u1+u2+u3=1;d1、d2为自定义得分值. 此外,基于时间相关性的考虑,如早上发生的事件与晚上发生的事件进行比较是没有多大意义的. 因此,不需要从序列的第一项一直比较到最后一项,只需要将一个序列中的事件eventi和另一序列中与eventi满足时空事件可比性的连续事件集进行比较即可. 序列可比性定义如下: 定义5时空事件可比性:已知两个时空事件序列L1={event11,event12,…,event1n}与L2={event21,event22,…,event2n},对于L1中任意一项event1i(1≤i≤n),若L2序列中存在连续事件event2j,event2(j+1),…,event2(j+a)(0≤a≤m-1,1≤j≤m-a),都满足关系Overlap(event1i,event2(j+a))、Contain(event1i,event2(j+a))、Equal(event1i,event2(j+a))、NoOverlap(event1i,event2(j+a))中的任意一种关系,则称L1中的事件event1i与L2中的连续事件event2j,event2(j+1),…,event2(j+a)具有时空事件可比性. 且序列L1中的事件event1i的下一事件event1(i+1)只需和L2中以事件event2j开始的事件逐一进行比较,而不用从序列L2的第一项开始比较. 基于此思想改进之后,序列进行的比较次数减少,改善了算法效率,而且还更符合实际意义. 基于NW算法的全局最优比对及时空事件相似度计算公式,下面给出时空事件序列相似度的定义. 定义6时空序列相似度:对于两个时空事件序列L1={event11,event12,…,event1n},L2={event21,event22…,event2n},有序列Li={event11,event12,…,event1i}与Lj={event21,event22,…,event2j}(Li⊆L1,Lj⊆L2)的比较得分S(i,j)计算公式如下. S(i,j)= (S(0,0)=0) (4) 通过公式可以求得时空序列相似度得分矩阵M,得分矩阵的最后一行最后一列数值即为两个时空序列L1、L2的相似度值. 具体求解过程如下. 算法1:多粒度时空序列比对算法MGSSA Input:Spatiotemporal event sequenceL1andL2,activity granularityi1, temporal granularityi2, spatial granularityi3; Output:Similarity ofL1andL2; Initialization:Set score matrixMto 0; 1:fori=0 to |L1| do 2:temp=0; 3: forj=0 to |L2| do 4: ifL1[i] andL2[j] satisfy the relationship of Contain, Overlap, Equal or NoOverlap 5: if(temp==0) 6: temp=j; 7: ifL1[i].activity andL2[j].activity belong to a class 8: if simactivity[i1]!=0 9: simactivity[i1]=MGAS(L1[i].activity,L2[j].activity,i1); 10: if simtime[i2]!=0 11:simtime[i2]= MGTS(L1[i].time,L2[j].time,i2); 12: if simposition[i3]!=0 13:simposition[i3]=MGSS(L1[i].position,L2[j].position,i3); 14: sim=u1simactivity[i1]+u2simtime[i2]+u3simposition[i3]; 15:M[i][j]=max(M[i-1][j-1]+sim,M[i-1][j]+d2,M[i][j-1]+d2); 16: else 17:M[i][j]=max(M[i-1][j-1]+d1,M[i-1][j]+d2,M[i][j-1]+d2); 18:j=temp; 19:returnM[|L1|-1][|L2|-1]; 该算法通过时空事件可比性的思想,减少序列事件的比较次数,通过分别求给定粒度下的活动、时间、空间相似度来度量事件的相似度,将每次求得的某种粒度下的活动、时间、空间相似度保存起来,当改变粒度时可以减少重复计算,提高算法效率. 下面具体介绍算法MGAS(multi-granularity activity similarity)、MGTS(multi-granularity time similarity)、MGSS(multi-granularity spatial similarity). 多粒度活动相似度算法MGAS,描述如下. 算法2:多粒度活动相似度算法MGAS Input:Activity typese1ande2of the spatiotemporal eventevent1andevent2in the sequence and the given activity granularity i; Output:Activity similaritySactivityofevent1andevent2; Initialization:The multi-way tree of activity type and a hashtable; 1:Find the nodes ofe1ande2in the multi-way tree, let them beaandb; 2: if Node(a,1)=Node(b,1) ∥the Node(x,y)indicates the yth parent of nodex 3: Find the ith parent nodes Node(a,i)and Node(b,i)ofaandb; 4: ifa.level<=i 5: Node(a,i)=a; 6: ifb.level<=i 7: Node(b,i)=b; 8: if Node(a,i)=Node(b,i) 9:Sactivity=1; 10: else ifa.level=b.level 11: Let num be be equal to the number of common nodes from the root node toaandb; 12:Sactivity=num/a.level; 13: else ifa.level≠b.level 14: maxlevel=max(a.level,b.level); 15: Let num be equal to the number of common nodes from the root node toaandb; 16:Sactivity=num/maxlevel; 17: returnSactivity; 算法2基于活动多叉树和通过整棵树构造出的一个哈希表. 由时空事件可比性的定义判断事件是否可比,然后判断两个事件的活动类型是否属于同一大类,满足以上两个条件的事件项根据给定活动粒度来求活动相似度,实现了从多种粒度来求活动相似度. 由于构造了哈希表,该算法空间复杂度较大,查找的时间复杂度为O(1). 对可求出活动相似度的两个事件求时间相似度、空间相似度. 在提出多粒度时间相似度算法之前,先给出事件时间关系权重的定义. 由于事件时间关系对两个事件的时间相似度是有影响的,根据事件时间关系的定义,下面给出事件时间关系权重定义. 定义7事件时间关系权重:若event1和event2为时空事件序列中的两个时空事件,这两个事件发生的时间信息分别为t1和t2,则这两个时空事件的事件时间关系权重RV(t1,t2)计算公式如下. (5) 多粒度时间相似度算法MGTS描述如下. 算法3:多粒度时间相似度算法MGTS Input:Time informationt1andt2of the spatiotemporal eventevent1andevent2in the sequence and the given temporal granularityi; Output:Time similarityStimeofevent1andevent2; 1:ifevent1andevent2satisfy the relationship of Contain, Overlap or Equal 2: Divide the time axis according to the given granularityi, and number from 1, thent1andt2can be represented by digital sequencel1andl2; 3: Calculate the longest common subsequenceLCS(l1,l2) of sequencel1andl2; 4:Si=|LCS(l1,l2)|/(|l1|+|l2|-|LCS(l1,l2)|); 5:Stime=Si*RelationshipValue(t1,t2); 6:else ifevent1andevent2satisfy the relationship of NoOverlap 7:Stime=1; 8:else 9:Stime=0; 10:returnStime; 算法3基于给定的某一粒度,将时间轴划分并编号,通过最长公共子序列LCS算法求出时间相似度,实现了以多种粒度来求时间相似度. 最长公共子序列算法经过优化后,时间复杂度为O(nlogn),所以算法3的时间复杂度为O(nlogn). 多粒度空间相似度算法MGSS描述如下. 算法4:多粒度空间相似度算法MGSS Input:Spatial informationp1andp2of the spatiotemporal eventevent1andevent2in the sequence and the given spatial granularityi; Output:Spatial similaritySspaceofevent1andevent2; Initialization:The multi-way tree of position and a hashtable; 1:Find the nodes ofp1andp2in the multi-way tree, let them beaandb; 2:Find the ith parent nodesNode(a,i) andNode(b,i) ofaandb; 3:ifNode(a,i)=Node(b,i) 4:Sspace=1; 5:else 6.Sspace=0; 7:returnSspace; 算法4基于空间类型多叉树和其构造的哈希表,同样也可从多种粒度来求空间相似度. 该算法的时间复杂度为O(1). 本文主要对产生时空事件序列的仿真环境进行简单介绍、对提出的多粒度时空序列比对算法MGSSA进行有效性验证,并将其与NW算法进行时间复杂度和相似度准确率的对比,最后将其作为距离度量方法来进行聚类分析. 实验采用的硬件环境为Win7操作系统,程序基于Visual Studio、Matlab平台和C++、Matlab语言实现. 本文的实验数据是通过本团队自行开发的智能环境仿真系统(smart environment simulator tool)[16]产生的,在该系统下可导入某个实际环境的布局,从而在其中放置智能节点,并对其中的两两智能节点进行连接,从构成智能节点网络,如图6所示. 图6 仿真环境展示Fig.6 Demonstration of smart environment simulator tool 本实验通过序列可视化方法来对多粒度时空序列比对算法进行有效性验证,如表1所示. 表1 序列可视化 为了验证有效性,本文做了4组实验,实验结果如表2所示,图7(a)以初始粒度显示了3条不同的序列,可以看出3条序列相似度较低. 改变空间粒度为SG(2),3条序列如图7(b)所示,从图7(b)可以看出L1与L2的轨迹相同,而L3则与L1、L2相异. 再次改变空间粒度为SG(1),3条序列如图7(c)所示,可以看出3条序列轨迹都相同. 在图7(c)的基础上改变活动粒度如图7(d)所示,可以看出不同事件序列之间,事件的活动类型大致相同,即原本不同的序列其实可以看作是同一序列. 表2 实验结果 图7 不同空间粒度、活动粒度对比Fig.7 Comparison of different spatial granularity and activity granularity 以上说明在不同的粒度下,时空序列之间的相似度也是不同的,序列的相似度是随着粒度的变化而变化的,在某一种粒度下序列之间差异大,而改变粒度后则可看作是相同的序列. 3.3.1时间复杂度 不进行粒度调整时,NW算法是从序列第一项到最后一项,一项一项进行比较,一条序列比个遍,所以NW算法的时间复杂度为O(n2). MGSSA算法根据序列项的可比性的思想,使得序列项的比较次数大大减少,改善了算法效率,所以从序列事件项的比较次数来看MGSSA算法优于NW算法. 但是MGSSA算法时间复杂度由序列事件项的比较次数和求解事件项相似度共同决定,求解事件项相似度方法的时间复杂度主要由多粒度活动、时间、空间相似度算法决定,所以MGSSA算法的最坏时间复杂度为O(n2logn). 在进行粒度调整时,MGSSA算法根据已有的计算结果可以快速调整出结果,即无需重新计算活动相似度、时间相似度或空间相似度,所以MGSSA算法的最好时间复杂度为O(n). 而NW算法每次则需要重新进行计算. 下面基于大量仿真得到的序列对两种算法进行运行时间比较实验,实验结果如图8所示,可知当时空事件序列数量为10、100、1 000时,MGSSA算法的平均运行时间均要少于NW算法,所以从平均时间复杂度对比结果来看,MGSSA算法要优于NW算法. 图8 MGSSA与NW算法的平均运行时间对比Fig.8 Comparison of average running time between MGSSA and NW 3.3.2语义完整性 NW算法仅是对字符之间的简单比较,字符比较相似度只有1和0的区分,对时空序列相似度计算较为片面和粗糙,缺乏语义方面的考量. 本文的MGSSA算法结合语义提出了新的活动、时间、空间相似度度量方法,能更好地度量事件相似度,反映的信息更丰富更全面,更能符合实际情况. 下面以本文提出的MGSSA算法为相似度计算方法,采用层次聚类法对时空序列进行聚类分析,实验以不同的图案代表不同的类. 从聚类结果中选取一些序列来进行说明,如表3所示,初始粒度下的聚类结果如图9(a)所示,L3与L6为同一类,L10与L28为同一类,而L1、L15、L20则各为一类. 改变活动粒度、空间粒度后,序列的聚类结果也随之改变,如图9(b)所示,可以看出,粒度变化后原本不在同一类的序列相似度变高,变成了同一类,L1、L3与L10为同一类,L6与L28为同一类,L15与L20为同一类. 本实验说明了本文提出的从多粒度多尺度计算时空序列相似度的模型是有效且合宜的. 表3 聚类结果比较 图9 初始聚类结果及改变粒度后的聚类结果对比Fig.9 Comparison of initial clustering result and clustering result after changing granularity 现有的关于用户行为分析很少有从不同粒度对时空事件序列进行相似度计算,从而缺乏对行为事件多粒度多视角的全面认知. 本文从大量的时空事件序列出发,在序列比对算法NW的基础上,设计了一种能从多粒度多角度计算时空序列相似度的算法MGSSA,该算法主要通过计算给定粒度下的时间相似度、空间相似度、活动类型相似度的加权平均来度量时空序列之间的相似度. 并且最后实验验证了该算法的有效性和可行性. 本研究为其他学者研究多粒度时空序列相似性提供了参考及指导.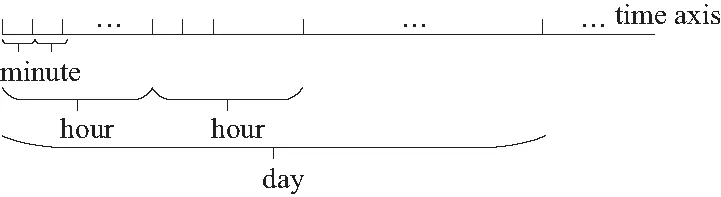
1.3 事件时间关系
1.4 序列比对Needleman-Wunsch算法
2 多粒度时空序列相似度计算
2.1 时空事件相似度及时空事件可比性
2.2 时空序列相似度及多粒度时空序列相似度求解算法
3 实验评估
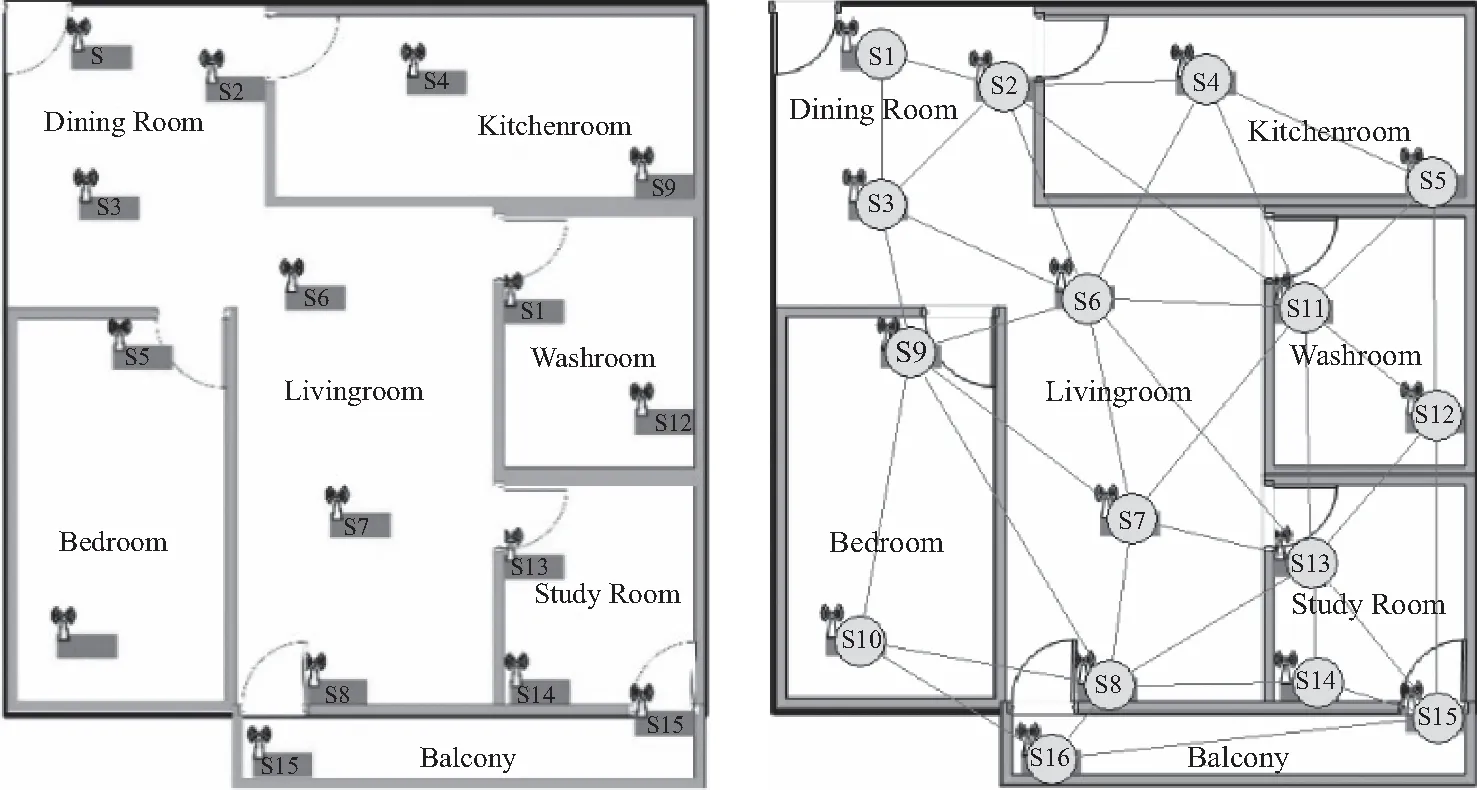
3.1 仿真环境介绍
3.2 MGSSA算法实验有效性验证


3.3 MGSSA算法与NW算法对比
3.4 聚类分析


4 结束语
