基于改进经验模态分解域内心动物理特征识别模式分量的心电信号重建*

牛晓东 卢莉蓉 王鉴 韩星程 郭树言 王黎明†

1) (中北大学,信息探测与处理山西省重点实验室,太原 030051)

2) (长治医学院物理教研室,长治 046000)

3) (长治医学院生物医学工程系,长治 046000)

心电图(electrocardiogram,ECG)诊断心脏疾病的严格标准,要求有效地消除噪声并准确地重建ECG信号.经验模式分解(empirical mode decomposition,EMD)方法重建ECG 信号中,模式混叠及重建采用模式分量的识别以经验为基础,导致重建ECG 信号准确度降低,且方法不具有自适应和通用性.本文首先基于积分均值定理提出一种改进的EMD 方法—积分均值模式分解(integral mean mode decomposition,IMMD)方法,经5000 个高斯白噪声样本的蒙特卡罗法验证,IMMD 方法比EMD 具有更优多分辨率分析能力,能够有效地缓解模式混叠.其次,基于ECG 信号内固有心动物理特征量识别重建ECG 信号所采用的模式分量,具有现实物理意义,因此,方法具有自适应和通用性.经验证,提出方法重建47 例ECG 信号与原ECG 信号的相关系数中: 31 例优于变分模式分解方法; 33 例优于Haar 小波软阈值法; 42 例优于集总经验模式分解方法; 45 例优于EMD 方法.相关系数均值为0.8904,方差为0.0071,表现稳定且最优.

1 引 言

心电图(electrocardiogram,ECG)记录的是心脏生理电活动信号,ECG 检查一般通过ECG 中P,QRS,T 特征波波形、时长及幅值识别诊断各种心脏疾病.例如P 波形状高尖,且振幅 ≥ 0.25 mV判断为右房肥大; P,R 间期延长 > 0.21 s 存在房室传导阻滞等[1].因此,ECG 信号轻微失真,也可能导致心脏疾病误诊.然而,ECG 信号是一种非线性、非平稳弱信号,极易被噪声污染.噪声一般包括两类: 50 Hz (在一些国家为60 Hz)电源线工频及由呼吸、电极或人体运动引起的基线漂移(baseline wander,BW)等窄带噪声; 主要由肌肉收缩引起的肌电干扰(muscle artifact,MA)等宽带噪声[2].两种噪声常常叠加引起ECG 信号畸变,严重影响ECG 诊断评估心脏病准确性,甚至导致诊断失效.严格的ECG 检查标准量以及ECG 信号的噪声特点,要求有效消除噪声后重建的ECG 信号具有高准确度.

窄带噪声频谱与ECG 信号频谱不重叠,常见线性和非线性信号处理方法都可有效校正[3−5],而宽带噪声全频域污染ECG 信号,导致严重特征波失真,成为ECG 信号消噪重点.迄今为止,已有多种非线性信号处理方法应用于消除宽带噪声并重建ECG 信号,但各种方法均存在缺点,重建准确度不令人满意.其中,自适应滤波需要额外地采集噪声相关参考信号[6]; 奇异值分解(singular value decomposition,SVD)[7]和小波阈值法[8,9]中,阈值过小消噪不理想,过大将导致波形严重畸变,并且阈值不能自适应噪声水平的波动[10].

经验模式分解(empirical mode decomposition,EMD)是一种自适应且数据驱动的非线性信号处理方法[11],可以克服SVD 和小波阈值法缺乏自适应的缺点,成为近年来生理信号[12]、医学图像[13]、特别是ECG 信号重建的研究热点.然而,EMD 域内重建ECG 信号存在两个问题: 1)瞬时模态分量(intrinsic mode function,IMF)之间的模式混叠,导致ECG 信号重建不准确.集总经验模式分解(ensemble empirical mode decomposition,EEMD)[14]以及变分模式分解(variational mode decomposition,VMD)[15]能够缓解模式混叠,并已应用于ECG 信号消噪和重建[16,17].然而,严格意义上,对每一个ECG 信号,EEMD 都需要预先多次测试并选择合适的辅助噪声幅度和数量;VMD 同样需要预先多次测试并选择合适的分解层数、平衡参数、噪声松弛等参数,因此,两种方法都不属于自适应且不具有通用性.2) 重建ECG 信号采用的模式分量基于工作者经验识别[18,19],不具有通用性.采用IMF 的香农熵、平均值、方差等统计特征量的阈值识别IMF,阈值也基于经验设置[20].

极值域模式分解(extremum field mean mode decomposition,EMMD)[21]是一种改进的EMD 方法.EMMD 采 用 积 分 均 值 定 理(integral mean value theorem,IMVT)求信号均值,能够增强分解信号能力,但EMMD 算法分解信号存在过分解问题.为了在EMD 域内进一步提高重建ECG 信号准确度,同时保证重建方法具有自适应和通用性,本文提出一种重建ECG 信号新方法.新方法首先改进EMMD,保留IMVT 均值方法并解决算法导致的过分解问题.为了区别于EMMD,本文将改进的EMMD 称为积分均值模式分解(integral mean mode decomposition,IMMD).经验证可以发现,IMMD 比EMD 具有更优的多分辨率分解能力,并且可以有效地缓解IMF 之间的模式混叠.其次,心电活动或心肌细胞的除极、复极过程对应一个完整的心动周期,因此,ECG 信号呈现心动的周期性波动,其IMF 分量同样表现出心动物理周期特征.本文采用心动物理周期特征识别属于ECG信号的IMF,识别方法符合ECG 信号的物理本质,并保证重建ECG 信号方法的自适应及通用性.

2 方法理论

2.1 IMMD 方法

设xi(t)(ti≤t≤ti+1,i=1,2,··· ,n −1) 为信号x(t) 相邻两个极值x(ti)和x(ti+1) 之间的局部,IMVT 求信号局部xi(t) 的均值为

mi(t)固定于局部中点.基于(1)式求出所有局部均值点后,三次样条插值所有均值点构建均值曲线m(t).

原型模式函数(proto mode function,PMF)[22]即为

上述过程称为一次均值筛选[11],PMF 记为PMF1.PMF1作为一个新信号,迭代重复均值筛选过程k(k= 2,3,···)次,得到PMFk.当PMFk满足柯西筛选停止准则[11]:

筛选停止,PMFk即为IMF1.将剩余分量r1(t)=x(t) – IMF1 作为新信号,重复上述所有过程得到IMF2.同理,可得其余IMF 分量及剩余分量r(t).

除局部均值外,EMMD 方法利用相邻两个局部均值mi(t)和mi+1(t)加权求取二者之间极值点ti+1处均值,即:

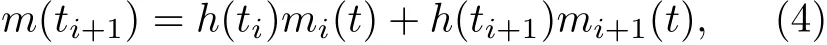
其中,

然而,m(ti+1)携带数据信息是mi(t)和mi+1(t)所携信息的重复.并且均值点数增加,极易导致样条插值构造均值曲线的不平滑,最终造成信号过分解.因此,IMMD 方法仅采用局部均值经三次样条插值构建均值曲线.

2.2 IMMD 方法的多分辨率分解信号能力

文献[23]研究了EMD 分解5000 个长度N=512,均值为0,方差为1 的高斯白噪声数据样本,得到如下结论: EMD 类似于小波变换Mallat 算法,等效于一个恒定品质因子Q的二分(或二进)滤波器组,具有多分辨率分解信号能力.本节将采用同样方法,分析IMMD 分解高斯白噪声特性,以此说明方法分解信号的性能.

IMMD 分解每个高斯白噪声样本,得到至少10 个IMF.对所有样本相应阶数IMF 求平均傅里叶功率谱,结果见图1(a).IMF1 相当于一个高通滤波器,其余IMF 等效于一组重叠带通滤波器,且后一IMF 等效带通滤波器中心频率约是前一 IMF等效带通滤波器中心频率的2/3.IMMD 方法分解高斯白噪声等效于滤波器组,且具有三分特性.

除IMF1 外,后一IMF 等效带通滤波器频带宽度大致是前一IMF 的2/3,所以等效带通滤波器组具有恒Q性质.因此,IMFs 的功率谱存在自相似性[23]:

图1 IMMD 和EMD 方法分解高斯白噪声的等效滤波器组特性 (a) IMMD (实线)和EMD (虚线)的IMF 分量的平 均 功 率 谱; (b) 基 于(5)式,IMMD (实 线)和EMD (虚线)的IMF 分量的平均功率谱坍缩重合Fig.1.Equivalent filter banks of IMMD and EMD decomposing Gauss white noises: (a) Averaged power spectra of IMFs from IMMD (solid curves) and EMD (dotted curves);(b) collapse and coincidence of the average power spectrum of IMFs from IMMD (solid curves) and EMD (dotted curves) based on Eq.(5).

其中Sk′(f) 是第k′个IMF 的 功率 谱(Sk(f) 是 第k个IMF 的功率谱),k′ >k≥2 ;ρ是常数,对于IMMD,ρ=3/2 ,对于EMD,ρ=2 .基于(5)式对平均功率谱标准化,所有带通IMF 的功率谱坍缩并重合为一条曲线.对于EMD,带通滤波器混叠较多低频成分,关于中心频率对称度差,窄带特性差,需要适当调整ρ值为2.01[24].对于IMMD,等效带通滤波器关于中心频率对称度及窄带特性明显优于EMD,两套等效带通滤波器组的平均功率谱标准化结果如图1(b)所示.

IMMD 分解高斯白噪声等效滤波器组具有三分特性,等效滤波器个数多于EMD (图1),滤波器组窄带特性及恒Q性质优于EMD,因此,具有更好的多分辨率分析能力.除上述5000 个高斯白噪声样本数据的蒙特卡罗方法实验外,本课题组基于大量数据实验,验证得到: 相比EMD,IMMD 具有更好的多分辨率分析能力,可以有效地缓解IMF分量之间模式混叠.

2.3 心动物理特征识别IMF

ECG 信号是记录人体心脏电活动信号,具有心动物理周期特性,其IMF 分量将呈现心动周期或心率(heart rate,HR)特征.

任一个IMF 分量可表达为[25]

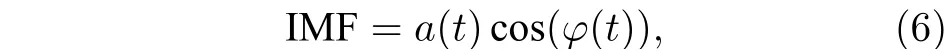
其中φ(t) 为IMF 频率调制,a(t) 为IMF 振幅调制.心动周期特征通过两种模式作用于IMF 分量:1) 属于ECG 信号的低阶IMF,心动周期特征作用于调幅a(t) .此时,IMF 分量的包络具有心动周期特性,包络的频谱中最大幅值对应频率等于HR.2) 属于ECG 信号的高阶IMF,心动周期特征作用于调频φ(t) .此时,IMF 具有周期性心动的谐波特性,频谱中最大幅值对应频率为HR 的整数倍(通常为1—3 倍).噪声属性IMF 分量不能表现上述两种心动周期特性.

2.4 IMMD 域内心动物理特征识别模式分量重建ECG 方法

1) 含噪ECG 信号经IMMD 分解为一套IMFs分量集合;

2) 求出每一个IMF 的上包络功率谱,若谱中最大幅值对应频率等于HR,则IMF 被识别为ECG信号分量;

3) 对步骤2 中未被识别为ECG 信号分量的IMF,求出每一个IMF 功率谱,若谱中最大幅值对应频率等于HR 整数倍,则IMF 也被识别为ECG信号分量;

4) 采用上述所有被识别为ECG 信号分量的IMF重建ECG 信号.

3 实验验证

3.1 105 ECG 信号[26]实验

选取MIT-BIH 心律失常数据库中105 ECG、压力测试数据库中BW 和MA 噪声[27],叠加构成含噪105 ECG 信号,采样频率为360 Hz,采样长度为3.6×103,HR 等于1.4 Hz,如图2 所示.可见,原105 ECG 信号的噪声污染程度较低,便于本节下述实验中的定量分析.

图3 含噪105 ECG 信号的IMF (蓝色曲线)及其包络(红色曲线)Fig.3.IMF envelopes (red curves) and IMFs (blue curves) of noisy No.105 ECG signal.

图2 实验采用信号波形 (a) 105 ECG 信号; (b) BW 信号; (c) MA 信号; (d)含噪105 ECG 信号Fig.2.Waveform of signals used in experiment: (a) No.105 ECG signal; (b) BW signal; (c) MA signal; (d) the noisy No.105 ECG signal.

图4 含噪105 ECG 信号IMFs 的功率谱(蓝色曲线),及IMFs 包络的功率谱(红色曲线)Fig.4.Power spectra of envelopes of IMFs (red curves) and of IMFs (blue curves) of noisy No.105 ECG signal.

IMMD 分解含噪105 ECG 信号得到IMF 分量及其包络如图3 所示,对应频谱如图4 所示.IMF1和IMF2 及其包络的频域中,幅值最高点处频率不等于1.4 Hz,因此没有表现出心动周期特征作用IMF 的两种模式(详见2.3 节),被识别为MA 噪声高频分量; IMF3—8 包络的频域中,幅值最高点对应频率等于心率1.4 Hz,符合心动周期特征作用IMF 的第一种模式; IMF9—12 的频域中,幅值最高点对应频率分别等于心率的3,3,2,1 倍,识别为ECG 信号谐波分量,符合心动周期特征作用IMF 的第二种模式; IMF13—r 没有表现出心动周期特征作用IMF 的两种模式,统一归类为低频噪声.产生的原因包括: MA 噪声低频分量,BW 噪声分量,IMMD 方法端点效应以及原105 ECG 信号的非零均值.经上述心动物理周期特征识别,IMF3—12 为ECG 信号分量,IMF1 和IMF2 为高频噪声,IMF13—r 为低频噪声.

为了显示所提出方法的能力,将本文方法同近年来常用VMD、小波软阈值法、EEMD 以及EMD重建105 ECG 信号进行对比,利用这五种方法重建的105 ECG 信号如图5 所示.由图5 可见,五种方法都很好地消除了BW 噪声.由于MA 噪声宽频特性,五种方法重建ECG 信号中仍然存在少量MA 噪声分量,特别是Harr 小波软阈值方法.EMD方法重建ECG 信号畸变最为严重,其次是EEMD.实际中,EEMD 对含噪105 ECG 信号的多次重建结果之间都有轻微不同,这是由辅助白噪声的随机性引起的[28].另外,VMD 方法中特征R 波的峰值失真比本文提出方法严重,例如,图5(b)中第10个R 波波峰峰值损失14.5%,本文方法为3.2%.

采用重建ECG 与原ECG 信号的相关系数R定量描述重建准确度,信噪比(signal-to-noise ratio,SNR)及均方误差(mean square error,MSE)定量描述消噪能力,五种方法重建105 ECG 信号R,SNR,MSE 的值如表1 所列.可 见,提出方法的R 和SNR 值最大,MSE 值最小,重建105 ECG 信号和消噪能力最优.

3.2 47 例含噪ECG 信号实验

为了进一步验证提出方法的有效性以及普遍适用性,选取MIT-BIH 心律失常数据库中其余ECG 信号(心律失常ECG 信号对应类型见表2),分别叠加BW 和MA 噪声,构成47 例含噪ECG信号(除去周期性极差的232 号),并采用上述五种方法重建47 例原ECG 信号.

图5 原105 ECG 信号(蓝色点虚线)与由五种方法重建的105 ECG 信号(红色实线) (a) 本文方法; (b) VMD; (c) Haar 小波软阈值; (d) EMMD; (e) EMDFig.5.Original No.105 ECG signal (blue dotted curves) and the No.105 ECG signals (red solid curves) reconstructed by 5 methods: (a) The proposed method; (b) VMD; (c) Haar wavelet with soft threshold; (d) EEMD; (e) EMD.

表1 五种方法重建105 ECG 信号的特征量值Table 1.Characteristic values of No.105 ECG signals reconstructed by 5 methods.

表2 实验采用的部分ECG 信号对应心律失常类型Table 2.Type of arrhythmia corresponding to some ECG signals used in the experiment.

由于大多数原ECG 信号本身含有一定量的低频和高频噪声,严重影响SNR 和MSE 值的准确度,因此,仅采用相关系数R对五种方法进行对比评估.利用五种方法重建5 组47 例ECG 信号与原ECG 信号的相关系数柱状图如图6 所示.其中,本文提出方法有31 例R值优于VMD,33 例R值优于Haar 小波,42 例R值优于EEMD,45 例R值优于EMD.

采用五种方法重建47 个ECG 信号的相关系数R值的统计盒形图如图7 所示,平均值及方差见表3.表3 中,本文提出方法对应相关系数均值最高,方差仅大于小波阈值.由图7 可见,本文提出方法明显优于其余四种方法.本文提出方法重建ECG 信号最为稳定、准确,其次为VMD,Haar小波阈值法,EEMD,EMD.

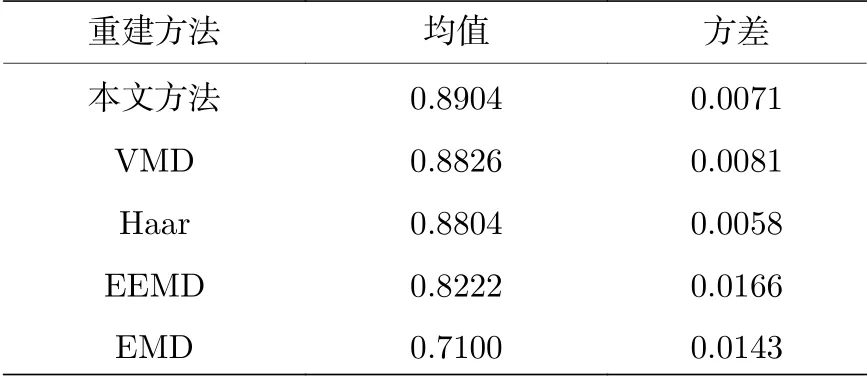
表3 五种方法重建47 个ECG 信号的R 值的均值与方差Table 3.Means and variances of R values of 47 ECG signals reconstructed by 5 methods.

4 讨论与结论

相比经验性包络相减法求均值(EMD,EEMD方法内),本文提出的IMMD 方法采用IMVT 求均值,具有严格的均值数学基础,因此,IMF 能够从信号中被准确地筛选剥离.经5000 个高斯白噪声样本的蒙特卡罗法统计验证,IMMD 方法具有比EMD,EEMD (同EMD 方 法 一 样,EEMD 具 有恒Q二分滤波器组特性[29])更优的多分辨率分解信号能力,可以有效缓解IMF 之间的模式混叠.

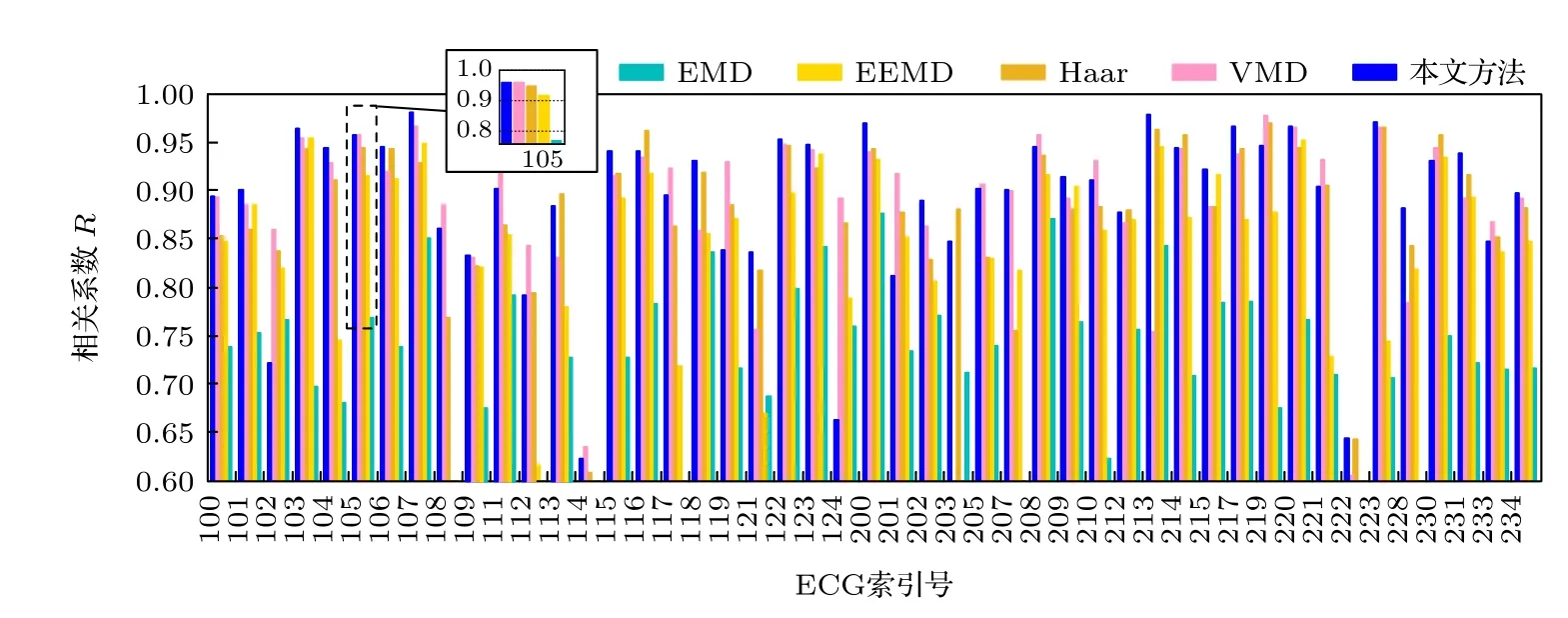
图6 采用五种方法重建47 个ECG 信号的R 值柱状图Fig.6.Histogram of R values of 47 ECG signals reconstructed by 5 methods.

图7 采用五种方法重建47个ECG信号的相关系数R 值的统计盒子图Fig.7.Five box-plots of R values of 47 ECG signals reconstructed by 5 methods.

另外,ECG 信号具有心动周期、心率等波动物理特征,ECG 信号的IMF 分量同样具有心动周期或HR 的特性.因此,本文方法中使用心动周期或HR 识别ECG 信号的IMF 分量,符合ECG 的物理本质特性.EMD,EEMD 和VMD 域内ECG 重建一般采用QRS 特征波经验性识别IMF,适用于时域中具有显著QRS 波动的IMF 识别(例如图3中IMF4).如果存在: 1) 时域中QRS 波动不显著但属于ECG 信号的低阶IMF (例如图3 中IMF3);2) 时域完全没有QRS 特征但属于ECG 信号的高阶IMF (例如图3 中IMF12),该方法识别错误.小波阈值法中固定阈值不能自适应小波系数不同局部内噪声水平波动,因此,重建ECG 信号可能存在局部消噪不理想(例如图5(c)).所以,本文提出方法,能够比上述四种方法进一步提高ECG信号重建准确度,且方法具有自适应和通用性.经47 例ECG 信号实验验证,提出的方法重建ECG与原ECG 信号相似度平均值为0.8904,方差为0.0071,且有31 例相似度值优于VMD,33 例相似度值优于Haar 小波,42 例相似度值优于EEMD,45 例相似度值优于EMD.本文提出方法重建ECG 信号能力体现了物理特征或现象在生物电信号处理中具有重要作用.

本方法中,建议通过含噪ECG 信号IMF 分量包络频谱图,经验确定HR.HR 可以通过严格的RR 波间隔得到,但需要大量算法实现.实际上,人心率一般为1—1.7 Hz (60—100 次/min).对于采集良好的ECG 信号,其IMF 分量包络的频谱图中,1—2 Hz 之间的幅度最大值对应频率即为HR,并且它常常出现在多个IMF 分量包络的频谱中,容易辨别(如图4 所示).本文选取的47 个ECG信号,都是基于上述经验方法确定HR.

提出的方法具有一定局限.对于极其特殊的232 ECG 信号(窦性心动过缓、一级房室传导阻滞和频繁异位心房运动,ECG 信号停顿持续长达6 s)重建,本文提出方法失效.关于心动周期特性极差的ECG 信号重建,以及从物理现象本质探索ECG信号处理,是本课题组下一步的工作.