考虑自旋-轨道耦合效应下SeH–阴离子的光谱和跃迁性质*

万明杰 柳福提 黄多辉

(宜宾学院理学部,宜宾 644007)

采用高精度的从头算方法研究了SeH–阴离子的基态(X1Σ+)和低激发的势能曲线、偶极矩和跃迁偶极矩.在计算中考虑了价-芯(CV)电子关联、Davidson 修正、标量相对论修正和自旋-轨道耦合效应(SOC).考虑了SOC 效应后,和态变为了弱束缚态.计算得到和跃迁具有很大的跃迁偶极矩.这三种跃迁都同时具有高对角分布的弗兰克-康登因子f00 及振动分支比R00.计算得到了和激发态的自发辐射寿命都很短,能够实现对SeH–阴离子的快速激光冷却.跃迁为三能级跃迁,中间态的存在对构建准闭合的循环能级的影响可以忽略.驱动和跃迁进行激光冷却SeH–阴离子的激光波长都在可见光范围内.本文的结果为以后激光冷却SeH–阴离子的实验提供了部分理论参考.

1 引 言

由于分子内部能级的复杂性,首次激光冷却分子的实验于2010 年实现,Shuman 等[1]采用横向激光冷却技术对SrF 分子进行了冷却.2013 年,Hummon 等[2]采用同样的技术实现了YO 分子的冷却.这是1 个三能级体系,其存在1 个中间态A′2Δ3/2.2014 年,Zhelyazkova 等[3]采用纵向激光冷却技术对CaF 分子进行了冷却.近十年,有很多学者对一系列的双原子分子进行了激光冷却的理论 研 究,如MgH[4],LiBe[5],CH[6],AlCl[7],OH[8],BaF[9]等.

相比于中性分子和分子阳离子,双原子分子阴离子具有更加复杂的能级,光谱数据非常缺乏,直到2015 年,Yzombard 等[10]才首次从理论上预测了激光冷却双原子分子阴离子的可能性.随后激光冷却阴离子吸引了越来越多学者的关注[11−16].鲁东大学的杨传路教授等预测了激光冷却NH–[11]和BH–[12]阴离子的冷却途径.Zeid 等[13]在自旋无关水平下计算了XH–(X = Mg,Ca,Sr,Ba)体系的势能曲线和跃迁偶极矩.XH–体系的↔ X1Σ+跃迁均具有很大的跃迁偶极矩和对角化的弗兰克-康登因子,他们认为这些阴离子可能是激光冷却的潜在候选体系.在我们前期的工作中,研究了激光冷却VI 簇氢化物的阴离子(OH–,SH–,TeH–)的可能性[14−16].SeH 在实验上和理论上都是一种重要的自由基,也是一种比较简单的重原子分子.本文将主要研究在考虑自旋-轨道耦合效应(SOC)下SeH–阴离子的光谱和跃迁性质,并讨论其激光冷却的可行性.

迄今为止,对SeH–阴离子的光谱常数的实验和理论研究很少.1987 年,Stoneman 和Larson[17]在磁场中采用光致分离技术观察SeH–阴离子,他们得到了SeH–基态的平衡核间距Re是SeH 分子基态1.0038(3)倍.同时采用最小二乘法得到了转动常数B 为7.7289 cm–1.1982 年,Brown 和Fackerell[18]采用CO 激光磁共振观察了SeD 和SeH 分子的振转光谱,得到了SeH 分子基态X2Π 的平衡核间距为1.4640715(25) Å.1987 年,Balasubramanian 等[19]采用二阶组态相互作用方法计算了SeH 和SeH+较低电子态的势能曲线,并得到了SeH 和SeH+基态的平衡核间距分别为1.467 Å和1.58 Å.1990 年,Binning Jr 和Curtiss[20]采用Hartree-Fock 方法计算得到SeH 基态的平衡核间距为1.463 Å.到目前为止,没有发现针对SeH–阴离子的跃迁性质的理论或实验研究.

本文将在SOC 水平下研究SeH–阴离子的基态(X1Σ+)和低激发的势能曲线和跃迁偶极矩,拟合得到各束缚态的光谱常数,预测其弗兰克-康登因子、振动分支比和自发辐射系数,最后讨论其激光冷却的可能性,并给出其冷却途径.

2 计算细节

本文采用从头算方法计算了SeH–阴离子4 个Λ-S 态的电子结构.在计算中增加了21Σ+态,以便比较11Π 和21Σ+态的能级高低.所有计算都在MOLPRO 2010 程序包[21]下完成.态对应于最低离解极限Se–(2Pu)+H(2Sg),第二离解极限为Se(3Pg) +H–(1Sg),其对应的电子态只能是3 重态,所以第二个1Σ+态对应于第三离解通道Se(1Du) + H–(1Sg).首先,采用限制性的Hartree-Fock 方法对SeH–阴离子进行波函数的初始猜测,得到初始波函数; 然后,采用完全活动空间自洽场方法(CASSCF)[22,23]产生多参考的波函数; 最后,采用多参考组态相互作用方法(MRCI)[24,25]得到各Λ-S 态的能量,同时也考虑了Davidson 修正[26].通过二阶Douglas-Kroll 哈密顿量[27,28]来考虑标量相对论效应.

在CASSCF 中,Se 原子的1s2s 壳层为冻结轨道,6 个分子轨道被选为活性轨道,包括H 原子1s和Se 原子4s4p5s 壳层,8 个电子占据了(4,1,1,0)活性轨道,写为CAS(8,6),Se 原子的1s2s2p3s3p为冻结轨道,Se 原子的3d 轨道为双占据的闭壳层.在MRCI 计算中,价-芯(CV)电子关联被考虑,CASSCF 过程中的闭壳层Se(3d)的10 个电子参与CV 关联计算.而Se 原子的1s2s2p3s3p 仍被冻结.此外,本文在MRCI+Q 水平下通过Breit-Pauli 算符[29]考虑了SOC 效应.在Λ-S 和Ω 态的所有计算中,Se 原子选择了aug-cc-pCVQZ-DK(ACVQZ-DK)全电子基组[30],H 原子选择了augcc-pVQZ-DK(AVQZ-DK)全电子基组[31].

采用LEVEL8.0 程序[32],通过求解径向薛定谔方程得到SeH–阴离子低电子态的光谱常数、弗兰克-康登因子、自发辐射系数和自发辐射寿命.

3 结果与讨论

3.1 势能曲线与光谱常数

计算了SeH–阴离子X1Σ+,a3Π,和b3Σ+态的势能曲线,这4 个电子态有1 个共同的离解通道Se–(2Pu) + H(2Sg).为了确定态的能级顺序,同时计算了第二个1Σ+态.它对应于第三离解通道Se(1Du) + H–(1Sg).所计算的电子态的势能曲线如图1 所示.可以看出11Π 是单重态的第一激发态,写为A1.

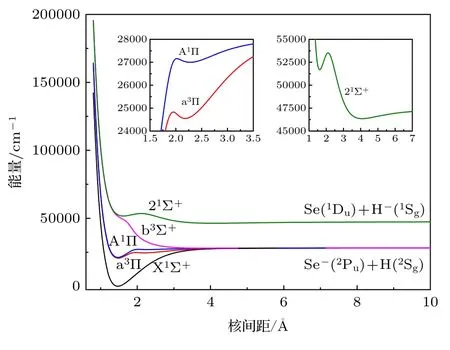
图1 X1Σ+,a3,A1,b3Σ+和21Σ+电子态的势能曲线Fig.1.Potential energy curves of the X1Σ+,a3,A1,b3Σ+,and 21Σ+ states.

SeH–阴离子的基态为X1Σ+,具有1 个很深的势阱,其离解能De为3.729 eV.X1Σ+态在平衡核间距Re处的主要组态为(1σ22σ23σ21π44σ25σ21π46σ22π41δ4)7σ28σ23π4,简写为(core)7σ28σ23π4,其权重为90.8%.Stoneman 和Larson[17]观察到SeH–基态的平衡核间距Re(X1Σ+)是SeH 分子Re(X2)的1.0038 倍.Brown 和Larson[18]测 得SeH 分 子基态X2的平衡核间距Re为1.464 Å.虽然Huber和Herzberg[33]收集了SeH 分子基态的实验值为1.475 Å,但结果不准确.本文的计算值为1.4694 Å(表1),只比实验值[17,18]小0.0002 Å,相对误差仅为0.01%.本文计算的转动常数Be为7.8507 cm–1,比采用最小二乘法拟合得到的实验值[17]大1.58%.可以看出本文计算结果与已有的实验值符合很好.同时基态的谐振频率(ωe)和非谐振频率(ωeχe)也列于表1 中,分别为2300.77 和46.10 cm–1.同时在MRCI+Q/AVQZ-DK 水平下计算了SeH–阴离子低激发态的势能曲线,在计算中没有考虑CV 关联效应,基态的光谱常数也列于表1 中,可以看出考虑CV 关联后,基态的光谱常数(Re,Be)和已有实验值符合的更好.

从图1 可以看到b3Σ+是1 个排斥态.其他3 个激发态都是具有双势阱结构的束缚态.a3Π,A1和21Σ+态的第一势阱分别位于比基态高20642.90,21240.75,51684.73 cm–1处,势阱深度分别为0.518,0.737,0.205 eV; 其平衡核间距Re分别为1.4679,1.4627,1.6113 Å.在平衡核间距位置处的主要组态分别为和(core)7σ28σα9σβ3π4,权重分别为91.32%,91.36%和88.28%.和X1Σ+→ 21Σ+跃迁主要是由3πx→ 9σ 和8σ →9σ 跃迁引起的.由于和21Σ+态电偶极矩的曲线非常平滑,没有发生突变,可以推测这3 个电子态都可能由预解离所致.从图1 可以看出这3 个态分别约在1.98,2.04,2.12 Å处发生预解离.a3Π,A1Π 和21Σ+态的第二势阱的平衡核间距Re分别为2.1787,2.2780,4.0808 Å.其势阱深度分别为0.450,0.147,0.135 eV.由于阴离子体系的光谱常数的实验值非常少,本文对比了第VI 主簇氢化物阴离子基态的光谱常数,分别列于表2 中,可以看出随着第VI 主簇原子质量的增加,其氢化物阴离子基态的平衡核间距Re逐渐地增大,但其氢化物阴离子基态的谐振频率ωe、非谐振频率ωeχe和势阱深度De都逐渐地减小.

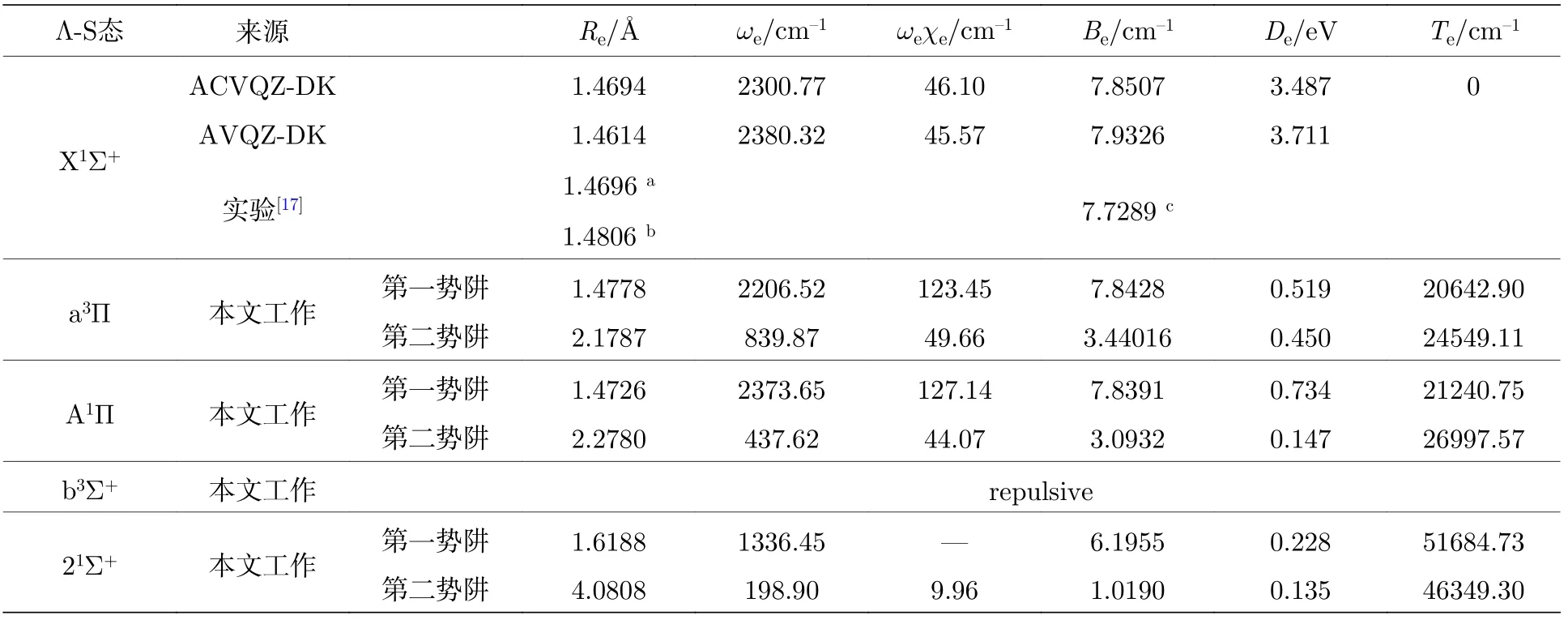
表1 Λ-S 的光谱常数Table 1.Spectroscopic parameters of the Λ-S states.

表2 第VI 主簇氢化物阴离子基态的光谱常数Table 2.Spectroscopic parameters of the ground state X1Σ+ of the Group VI-hydride anions.

考虑SOC 效应后,Se–离子的2P 原子态分裂为2P1/2和2P3/2态.和态对应于Se–(2P3/2) + H(2S1/2)离解通道,态对应于Se–(2P1/2) + H(2S1/2)离解通道.本文预测了Se–(2P)原子态的分裂常数,ASO(2P1/2–2P3/2) = 2303.77 cm–1.另外,对应于较高的离解通道Se(1D2) + H–(1S0),其与最低离解通道的相对能量为20032.24 cm–1,比实验值[34−36]大241.36 cm–1,相对误差仅为1.22%,本文计算值与已有实验值符合很好.Ω 态之间的离解关系列于表3.表3 也同样可以看出考虑CV 关联效应后,第三离解极限与最低离解极限的相对能量和已有实验值符合得更好.

9 个Ω 态的势能曲线如图2 所示,所计算的电子态都是束缚态,各Ω 态的光谱常数列于表4.对比表2,基态的势阱深度比X1Σ+态的要小约0.1 eV.从图2 可看出和态 具 有2 个 势 阱.态 是 第 一激发态,其第一势阱到基态的垂直跃迁能为19787.17 cm–1.态的第一势阱的分裂常数为:= 249.1 cm–1,1436.25 cm–1,= 4.60 cm–1.而a3Π 态的第二势阱具有更大的分裂常数,和 a3Π0−态之间的分裂常数达到了192.26 cm–1.从图2 还可以看出和在2.89 Å处交叉.考虑SOC 效应后,b3Σ+态的2 个分裂态和态都具有了1 个很浅的势阱,势阱深度分别为0.096 和0.066 eV,平衡核间距分别为3.1807和3.2046 Å,这两个态都有较大的谐振频率,均超过200 cm–1,说明这2 个分裂态都是弱束缚态.同时可以预测处b3Σ+态的分裂常数为239.22 cm–1.同样态的第二势阱也是弱束缚态.由于的势阱太小,可以认为其由弱束缚态变为排斥态.由于和b3Σ+态的分裂常数很大,可以看出SOC 效应对SeH–阴离子的势能曲线和光谱常数的影响很大.

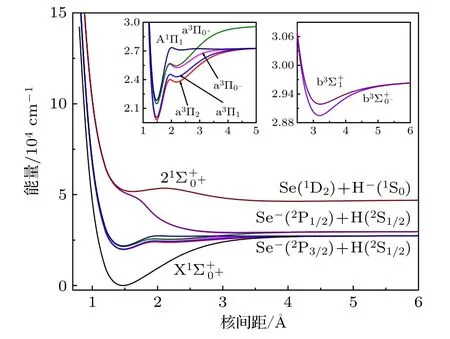
图2 9 个Ω 电子态的势能曲线Fig.2.Potential energy curves of nine Ω states.

表3 Ω 态的离解关系Table 3.Calculated dissociation relationships of the Ω states.

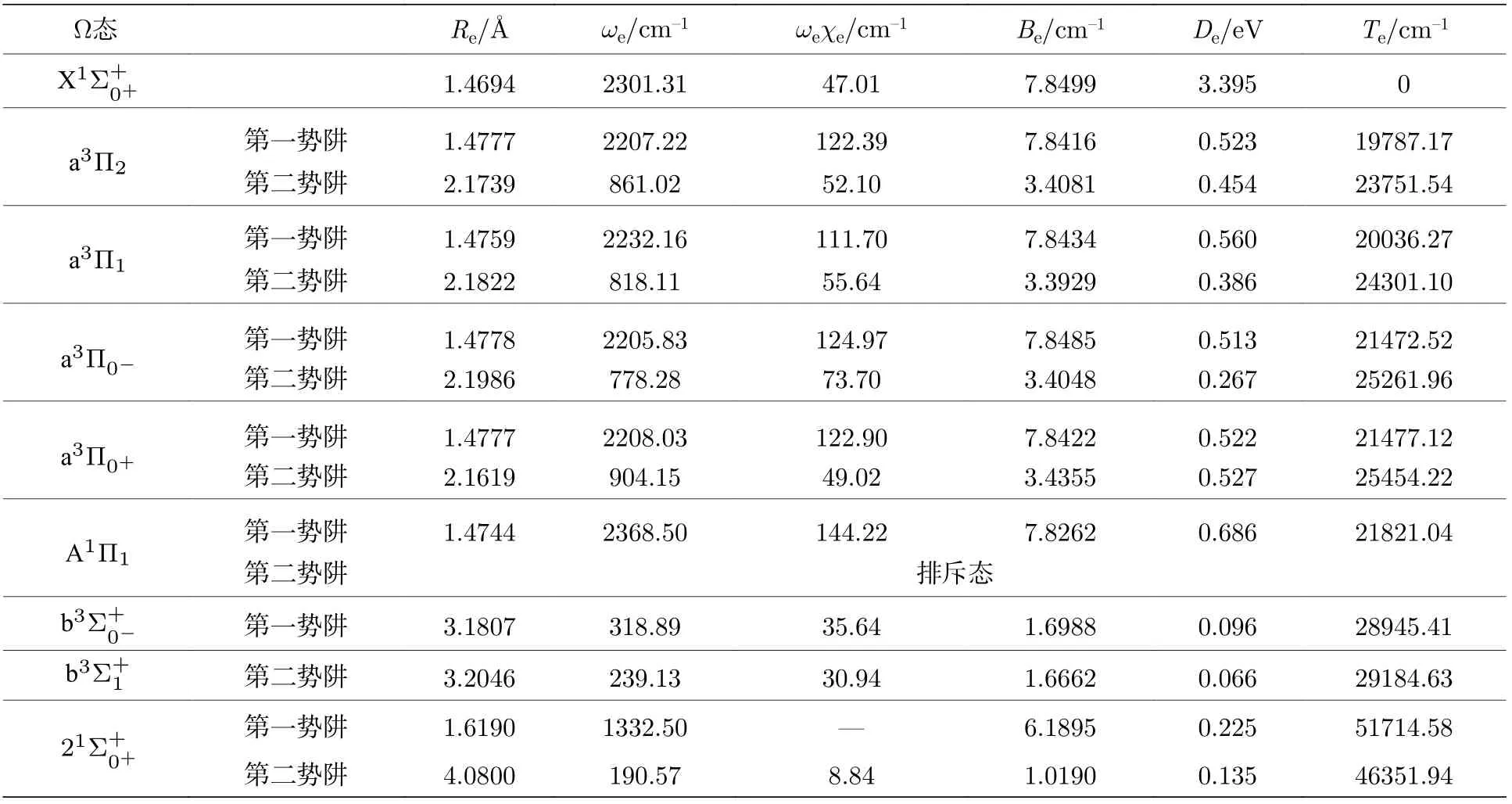
表4 Ω 电子态的光谱常数Table 4.Spectroscopic parameters of the Ω states.

3.2 Ω 态的跃迁偶极矩

图3 a 31 ↔X1Σ+0+ ,a 30+ ↔X1Σ+0+ ,A 11 ↔X1Σ+0+ ,A11 ↔a31 和 A 11 ↔a30+ 跃迁的跃迁偶极矩Fig.3.Transition dipole moments of the a 31 ↔X1Σ+0+ ,a30+ ↔X1Σ+0+ ,A 11 ↔X1Σ+0+ ,A 11 ↔a31 ,and A11 ↔a30+ transition.

3.3 振动分支比及激光冷却SeH–阴离子的可能性

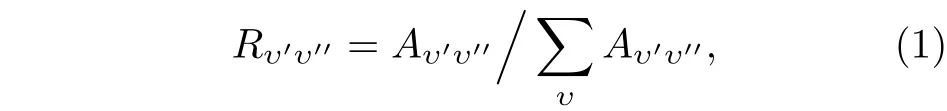
其中,Aυ′υ′′表示和跃迁的自发辐射系数.表5 列出了以上3 种跃迁的弗兰克-康登因子、自发辐射系数和振动分支比.本文分别讨论自旋阻禁和直接跃迁2 种情况来进行激光冷却SeH–阴离子的可能性.

3.3.1 自旋阻禁跃迁

表5 a 31 ↔X1Σ+0+ ,a 30+ ↔X1Σ+0+ 和 A 11 ↔ X 1Σ+0+ 跃迁的辐射系数 A υ′υ′′ 、弗兰克-康登因子 f υ′υ′′ 和振动分支比Rυ′υ′′Table 5.Emission rates A υ′υ′′ ,Franck-Condon Factors f υ′υ′′ ,branching ratios R υ′υ′′ of the a 31 ↔X1Σ+0+ ,a30+ ↔X1Σ+0+ ,and A 11 ↔ X 1Σ+0+ transitions.

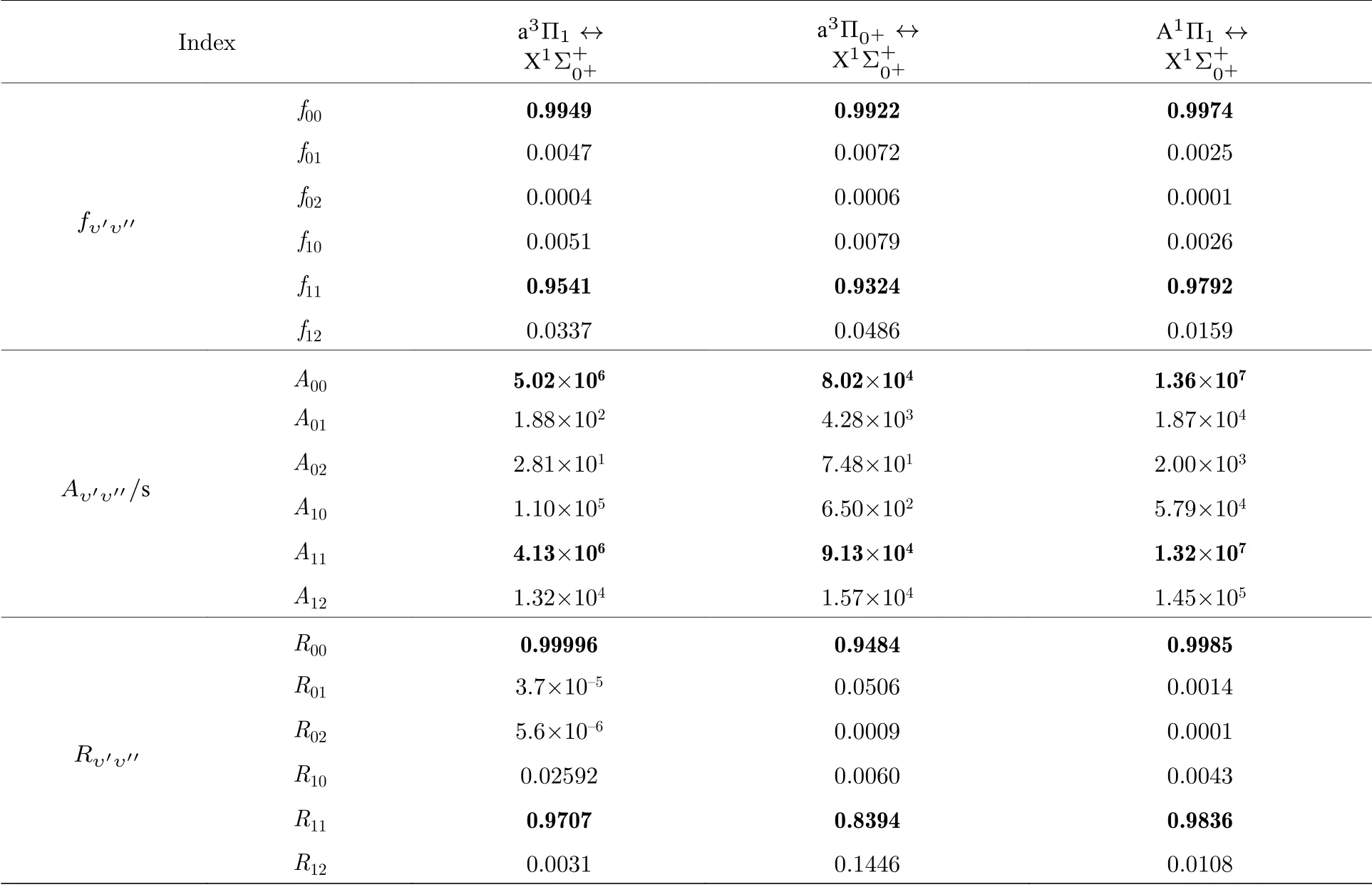
表5 a 31 ↔X1Σ+0+ ,a 30+ ↔X1Σ+0+ 和 A 11 ↔ X 1Σ+0+ 跃迁的辐射系数 A υ′υ′′ 、弗兰克-康登因子 f υ′υ′′ 和振动分支比Rυ′υ′′Table 5.Emission rates A υ′υ′′ ,Franck-Condon Factors f υ′υ′′ ,branching ratios R υ′υ′′ of the a 31 ↔X1Σ+0+ ,a30+ ↔X1Σ+0+ ,and A 11 ↔ X 1Σ+0+ transitions.

Index a3Π1 ↔X1Σ+0+a3Π0+ ↔X1Σ+0+A1Π1 ↔X1Σ+0+fυ′υ′′f00 0.9949 0.9922 0.9974 f01 0.0047 0.0072 0.0025 f02 0.0004 0.0006 0.0001 f10 0.0051 0.0079 0.0026 f11 0.9541 0.9324 0.9792 f12 0.0337 0.0486 0.0159 Aυ′υ′′/s A00 5.02×106 8.02×104 1.36×107 A01 1.88×102 4.28×103 1.87×104 A02 2.81×101 7.48×101 2.00×103 A10 1.10×105 6.50×102 5.79×104 A11 4.13×106 9.13×104 1.32×107 A12 1.32×104 1.57×104 1.45×105 Rυ′υ′′R00 0.99996 0.9484 0.9985 R01 3.7×10–5 0.0506 0.0014 R02 5.6×10–6 0.0009 0.0001 R10 0.02592 0.0060 0.0043 R11 0.9707 0.8394 0.9836 R12 0.0031 0.1446 0.0108

图4 激光冷却SeH–阴离子的方案 (a) a 31 ↔X1Σ+0+ 跃迁; (b) a 30+ ↔X1Σ+0+ 跃迁Fig.4.Proposed laser cooling scheme: (a) Using the a 31 ↔X1Σ+0+ transition; (b) using the a 30+ ↔X1Σ+0+ transition.

3.3.2 三能级跃迁

图5 采用 A 11 ↔X1Σ+0+ 跃迁进行激光冷却SeH–阴离子的方案Fig.5.Proposed laser cooling scheme by using the A 11 ↔X1Σ+0+ transition.

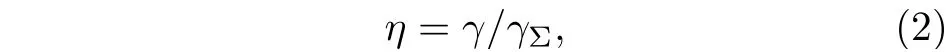
其 中,对 于SeH–阴 离 子,γ1和γ2分 别 表 示和跃迁的自发辐射系数.本文的计算值分别为2.31 和1.21×10–2s–1.γΣ表示态的自发辐射速率.这样可以得到η1=γ1/γΣ< 2.0×10–7,η2=γ2/γΣ<9.0×10–10,本文的计算结果远远小于YO 分子的振动分支损失比(< 4×10–4)[2].结果表明中间态的存在对激光冷却SeH–阴离子几乎没有影响.可以选取一束主激光来驱动跃迁时,理论上散射光子数仅为600 个.其主激光波长为459.52 nm.为了提高冷却效率,增加了两束抽运激光λ10= 511.88 和λ21= 512.83 nm,其理论上散射光子数可达到3.3×105个.相应的三能级跃迁进行激光冷却SeH–阴离子的冷却途径如图5所示.

4 结 论

在MRCI+Q/AVQZ-DK 水 平 下,本 文 计 算了SeH–阴离子5 个Λ-S 态和9 个Ω 态的势能曲线.计算中考虑了标量相对论效应和CV 关联效应.考虑SOC 效应后b3Σ+态的2 个分裂态变为了弱束缚态.所有电子态的光谱常数都是首次报道.阻禁跃迁和三能级跃迁都具有高对角分布的弗兰克-康登因子和振动分支比.并且和态的自发辐射寿命都很短,能快速地冷却SeH–阴离子.中间态和的存在不影响构造准闭合的循环跃迁.驱动跃迁只需要一束主激光,由于振动分支比不够大,驱动和跃迁需要增加两束抽运激光.所有的激光波长都在可见光的范围内.本文预测SeH–阴离子是适合激光冷却的潜在体系.