大尺度洛伦兹破缺与空间平坦性

李 静,薛 迅,2

（1. 华东师范大学 物理与电子科学学院, 上海 200241; 2. 新疆大学 理论物理中心, 乌鲁木齐 830046）

0 引 言

其中, 宇宙学密度.辐射为主的早期, 有ρa4=const (常数), 式(1)等号右边正比于a2; 在物质为主的阶段, 则有ρa3=const, 式(1)等号右边正比于a. 宇宙从极早期演化到现在, 无论在哪个时期, 宇宙尺度因子都是在不断增长的. 如果K0, 那么式(1)等号左边表达式的绝对值就应该不断增长. 宇宙的演化从普朗克时期也就是t=10−43s 到目前,a(t) 已经增大了几十个量级, 那么的值也增大了几十个量级. 观测到目前Ω对1的偏离最多为1的量级, 那么现在的值也应该是1的量级. 按照宇宙的演化规律逆推, 得到普朗克时期的宇宙学密度Ωp=1±10−N, 其中N是1个至少为几十的正数. 这说明在普朗克时期结束时, 临界密度和宇宙物质密度在很多位有效数字上是相同的, 而这两个量又不完全相等. 否则, 宇宙就不可能经过漫长的演化而具有现在的空间准平坦性.

将Ia型超新星作为标准烛光得到了宇宙是在加速膨胀的结论. 大尺度观测表明, 宇宙加速膨胀发生在较晚的时刻[1]. 因此, 人们提出了几种尝试来描述宇宙加速膨胀的方法. 通常, 对此有两种解释:一种是假定一个具有负压的能量, 称之为暗能量; 另一种是修正引力理论. 基于这两种解释, 人们又提出了许多模型. 但是由于参数空间的简并性, 很难确定哪一个模型是对的, 其中 ΛCDM 模型在一定程度上能够解释观测数据[2].

基于 ΛCDM 模型的假设,CMB的观测可以得到H0=(67.27±0.60)km/(s·Mpc)[1], 这与许多早期的H0估计值是相容的. 相反, 搭建距离阶梯的局域测量得到的更高的H0值, 误差棒较大. 来自超新星和SH0ES的最新测量结果为H0=(73.52±1.62)km/(s·Mpc), 这与 CMB测量数据有超过 3σ的差距[3],这是现代宇宙学中最难以解决的问题. 人们已经提出了多种方法来解决这个问题, 例如引入一个超越标准 ΛCDM 模型的新宇宙模型.

本文想要弄清楚的是当前的观测数据是否能够容纳一个空间曲率不为0的宇宙学模型. 当前的宇宙学观测支持宇宙是空间平坦的, 例如结合Planck2018宇宙微波背景( CMB )和重子声学振荡测量,得到ΩK=0.001±0.002[1]. 但是, 这些约束条件是基于特定宇宙学模型(如标准 ΛCDM 模型)的预先假设. 需要注意的是, 暗能量和空间曲率的观测约束是相互依赖的, 当人们试图同时约束这两个量时, 往往会出现简并[4], 因此很难同时约束这两个量. 一般来说, 在估计空间曲率的时候, 会直接将暗能量假设为不变的宇宙学常数; 反过来, 在分析暗能量的时候, 会直接假设宇宙是空间平坦的. 实际上, 如果暗能量的密度是随着时间变化, 那么宇宙的几何限制会变得更加宽泛, 甚至可能取决于暗能量的早期性质[5]; 即使实际的空间曲率很小, 直接假设宇宙是空间平坦的也可能会构建错误的暗能量状态方程.简单地将暗能量看作是不变的宇宙学常数, 是不能辨别暗能量状态方程是否是动力学的[6]. 进一步来说, 最新的SneIa数据与空间平坦的 ΛCDM 假定之间导致的H0的紧张关系[7]最终可能支持空间非平坦宇宙[8].

通常认为, 选择空间非平坦宇宙是因为早期的暴涨导致今天的宇宙几乎空间平坦, 但是空间曲率并不是完全等于0的. 如果e-折数不是很大, 空间平坦性就不是必要的[9]. 研究晚期宇宙时, 空间曲率可能仍然对Friedmann方程有贡献, 尽管观测表明空间曲率的贡献比其他能量分量小得多.

最近的观测结果使问题变得更加复杂. 观测表明宇宙膨胀的减速因子是随着时间变化的, 大约在60亿年前, 宇宙从减速膨胀变成了加速膨胀. 在 ΛCDM 模型中, 宇宙学常数可以看成是来自真空能量密度, 是导致宇宙加速膨胀的原因. 在考虑了大尺度洛伦兹破缺以后[10], 洛伦兹破缺效应所导致的大尺度挠率分布结合真空能量密度共同产生了宇宙后期的加速膨胀. 因此, 我们可以定义一个引起宇宙后期加速膨胀的有效真空能量密度: 利用物质密度ΩM的演化与初值条件将裸的宇宙学常数Λ0限制在一个可取范围内; 再利用有效真空能量密度, 将不同空间曲率取值下的Λ0限制在合理范围之内. 在允许的取值范围下, 讨论空间不平坦的大尺度洛伦兹破缺模型的表现.

1 大尺度洛伦兹破缺下的引力理论

文献[10]讨论了空间曲率为0的大尺度洛伦兹破缺宇宙模型. FRW(Friedmann-Robertson-Walker)度规的形式为

引力场运动方程为

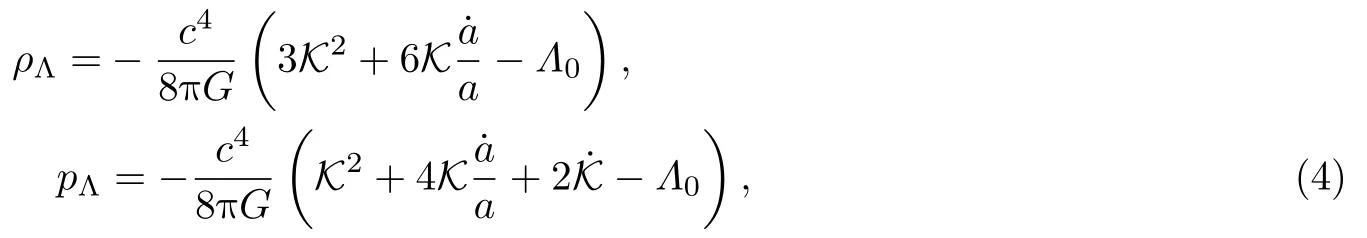
和

本文旨在探讨基于空间不平坦条件下大尺度洛伦兹破缺模型的表现. 需要注意的是模型缺乏K(t)的演化机制, 方程组(5)和(6)并不封闭. 洛伦兹破缺的区域经历了随暴涨尺度超出视界, 后期再重入视界的过程. 由此导致K(t) 的动力学演化, 原则上需要借助具体的量子引力和暴涨模型才能给出其预言. 但是唯象地, 借助 ΛCDM 这个唯象模型或者是假定暗伴满足某一状态方程, 可以对K(t) 的动力学演化给出近似. 具体地, 可以将 ΛCDM 模型Friedmann方程中独立的一个加入修正的Friedmann方程使方程组封闭, 有两种选择, 得到两种近似情形. 加入暗伴状态方程, 封闭方程组可以做出第三种近似, 文献[11]给出了3种近似, 具体如下.

第一种近似(CaseA),

第二种近似(CaseB),

第三种近似(CaseC),

式(7)–式(8)中 Λ为借助 ΛCDM 模型, 由天文或者宇宙学观测所定出的宇宙学常数的观测值, 即以当前的观测值来表示裸宇宙学常数.

注意区别: w 为宇宙介质的状态方程参数, 即 p=wρ; w0为暗伴的状态方程参数, 即 pΛ=w0ρΛ.

ΛCDM 的Friedmann可以写为

类似地, 将大尺度洛伦兹破缺模型的Friedmann方程改写为

对比式(10)和式(11), 在大尺度洛伦兹破缺模型中对宇宙加速膨胀起作用的不仅是裸宇宙学常数 Λ0,还有来自 K(t) 的贡献, 其总的贡献可以定义有效宇宙学常数

来刻画. 同样借助ΛCDM模型的Friedmann方程可以得到K(t)的初始条件. 当前时刻的contortion有两种取值可能, 分别是

为第一种初值;

从式(15)可以看出, 对于一个具体的大尺度洛伦兹破缺模型, 需要输入曲率常数 K 、当前时刻的宇宙尺度因子 a0、哈勃常数 H0和裸的宇宙学常数 Λ0. 在后文中以宇宙学常数的观测值Λ的倍数关系来表示裸宇宙学常数Λ0.

由于加速膨胀发生在宇宙的后期, 我们只考虑物质为主的时期, 在 ω=0 的情况下, 结合大尺度洛伦兹破缺模型的Friedmann方程、3个近似条件, 以及 K(t) 的初始条件, 可以得到哈勃参数 H(t) 和contortion 的演化. 在不同的取值情况下, 哈勃参数 H 随着宇宙尺度因子 a 的演化情况见图1–图3.

将图1给出的3种近似情况下哈勃参数随着宇宙尺度因子的演化曲线与 ΛCDM 模型的演化进行比较, 可以看出, CaseC2的演化与其他模型的演化之间有比较大的差异; 在宇宙尺度因子为1以后,各个模型的演化结果差异很小; 从整体来看, CaseB与 ΛCDM 模型的演化结果趋近于完全相同.

从图2和图3可以看到, 在 K=−1的情况下CaseA2与CaseC2的演化与 ΛCDM 模型差异比较大, 同时CaseA1、CaseB1、CaseC1、CaseB2与 ΛCDM 模型之间的差异很小. 结合图1、图2和图3来看, 在 K=−1,K(t)取第一种初值的情况下, 3种近似情况都与 ΛCDM 模型的演化情况非常接近.

由于光线还是沿着测地线运动, 所以大尺度洛伦兹破缺模型的红移公式与ΛCDM模型一样, 即

图1 K=+1,Λ0=−0.02Λ, a0H0=3.5的情况下, 哈勃参数随尺度因子的演化Fig. 1 The Hubble constant changes with the scale factor whenK=+1,Λ0=−0.02Λ,a0H0=3.5

图2 K=−1,Λ0=−0.02Λ,a0H0=3.5 的情况下, 哈勃参数随尺度因子的演化Fig. 2 The Hubble constant changes with the scale factor whenK=−1,Λ0=−0.02Λ,a0H0=3.5

根据光度距离dL的定义, 可以得到

其中,dL为光度距离,为哈勃距离,为当前的曲率密度. 转化为以红移z为变量的,K(z) 与dL(z) 的方程组为

图3 K=−1,Λ0=−0.02Λ,a0H0=3.0和 a0H0=2.5 的情况下, 哈勃参数随尺度因子的演化Fig. 3 The Hubble constant changes with the scale factor when K=−1,Λ0=−0.02Λ,a0H0=3.0 and2.5

定义距离模数

其中, Mpc是兆秒差距, 公式中的这一步代表无量纲化. 不同取值情况下, 光度距离dL随着红移的演化见图4.

图4 K=+1,w0=−1,a0H0=3.5,Λ0=−0.02Λ 的情况下, 光度距离随着红移的演化Fig. 4 The luminosity distance changes with redshift whenK=+1,w0=−1,a0H0=3.5,Λ0=−0.02Λ

从图4给出的不同近似模型的光度距离随红移的演化结果中可以看出, CaseA、 CaseB与ΛCDM模型的演化差距比较小, CaseC与 ΛCDM 模型的演化差距较大.

2 计算结果与数据分析

由大尺度洛伦兹破缺模型的Friedmann方程可以得到

在K=+1和K=−1两种情况下, 不同的a0H0对应的最小的Λ0取值Λmin见图5.

根据修正的Friedmann方程, 对于所有的近似情况, 可以得到物质密度ΩM随着时间的演化过程.3种近似在不同的Λ0取值下,ΩM的演化见图6.

随着Λ0的增加,ΩM会出现小于0的情况. 为了保证ΩM≥0, 也就是模型必须满足, 从而求解出Λ0的最大取值Λmax. 它表示在宇宙尺度因子为 0.01a0至 20a0的范围内,Λ0的取值大于Λmax就会出现ΩM小于0的情况. 表1和表2列出了不同取值情况下的Λmax.

图5 不同的 a0H0对应的 Λmin : a) K=+1; b) K=–1Fig. 5 Λmin changes with a0H0 : a) K=+1; b) K=–1

图6 K=+1, a0H0=3.5,Λ0=−0.02Λ 情况下, 物质密度 ΩM 随尺度因子的演化Fig. 6 The matter density ΩM changes with the scale factor when K=+1, a0H0=3.5,Λ0=−0.02Λ

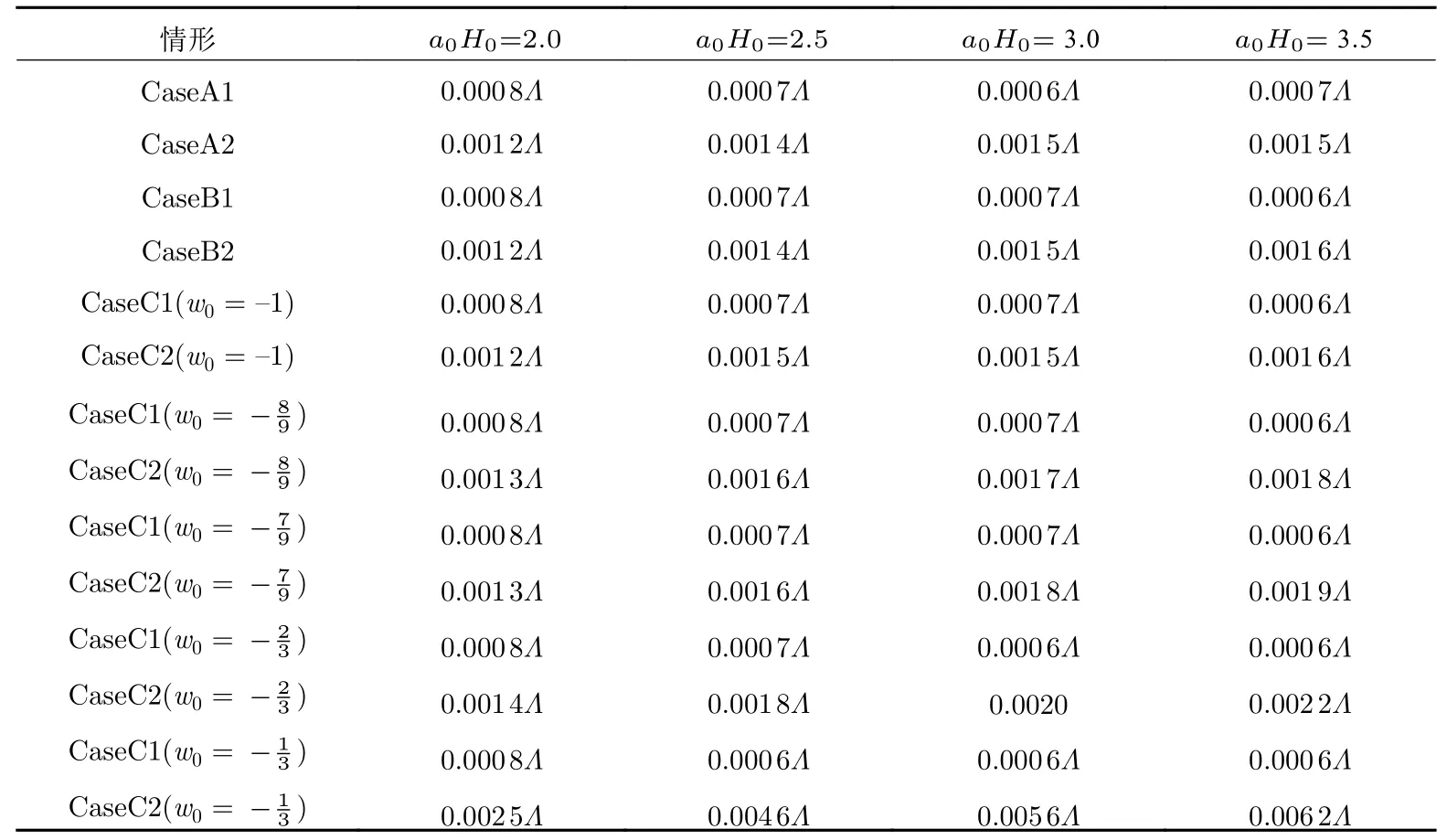
表1 K=+1情况下 Λmax 的值Tab. 1 The value of Λmax whenK=+1

可以看到,Λ0的取值大于0时都会出现ΩM小于0的情况. 因此将Λ0的值限制在小于0 的范围,也就是说Λmax≈0.

文献[11]探讨了在不同的Λ0取值下,Λeff演化行为的变化, 发现对所有的近似情况都存在Λ0的临界值Λ0-crit, 当Λ0<Λ0-crit时,Λeff的行为为随时间单调下降, 当Λ0>Λ0-crit的时候Λeff的演化存在局域极小, 并且Λ0-crit取值近似为0; 归结起来, 其结论为当Λ0来自弦景观时,Λeff单调下降, 当Λ0来自沼泽地时,Λeff具有局域极小. 文献[12]表明, 如果用基于标量quintessence场的势能V(ϕ)模拟Λeff,当Λ0来自弦景观时,V(ϕ)为单调下降的quintessence势,Λ0来自沼泽地时,V(ϕ) 为有局域极小的亚稳de Sitter势. 我们在这里研究了K=+1,K=−1的Λ0-crit随Λ0的取值不同而产生的变化, 表3和表4给出了其数值结果, 具体的解如图7所示. 从图5可以看到, 在K=+1的情况下,a0H0<2时,Λmin>0, 也就是说此时出现了Λmin>Λmax, 因此不需要讨论K=+1,a0H0≥2 的Λ0-crit情况.

表2 K=−1情况下 Λmax 的值Tab. 2 The value of Λmax whenK=−1

表3 K=+1 时Λ0-crit的值Tab. 3 The value of Λ0-crit whenK=+1

表4 K=−1 时Λ0-crit的值Tab. 4 The value of Λ0-crit when K=−1

图7 K=+1,a0H0=3.5情况下,Λeff 从单调下降的quintessence类型到出现局域极小类型的转变Fig. 7 Λeff transitions from a monotonically decreasing quintessence type to a local minimum type with changes in the scale factor whenK=+1,a0H0=3.5

从图8–图13可以看到, 在我们限制的Λ0取值范围内, 在不同的空间曲率取值下, 3种近似情况下, 距离模数的理论预测值都在观测误差之内. 也就是说, 观测结果并不能对我们的模型进行有效的筛选.

图8 K=+1,Λ0=−0.02Λ,a0H0=3.5 情况下, 距离模数的模型预言值与测量值的对比Fig. 8 Comparison of the measured distance modulus with its expected value when K=+1,Λ0=−0.02Λ,a0H0=3.5

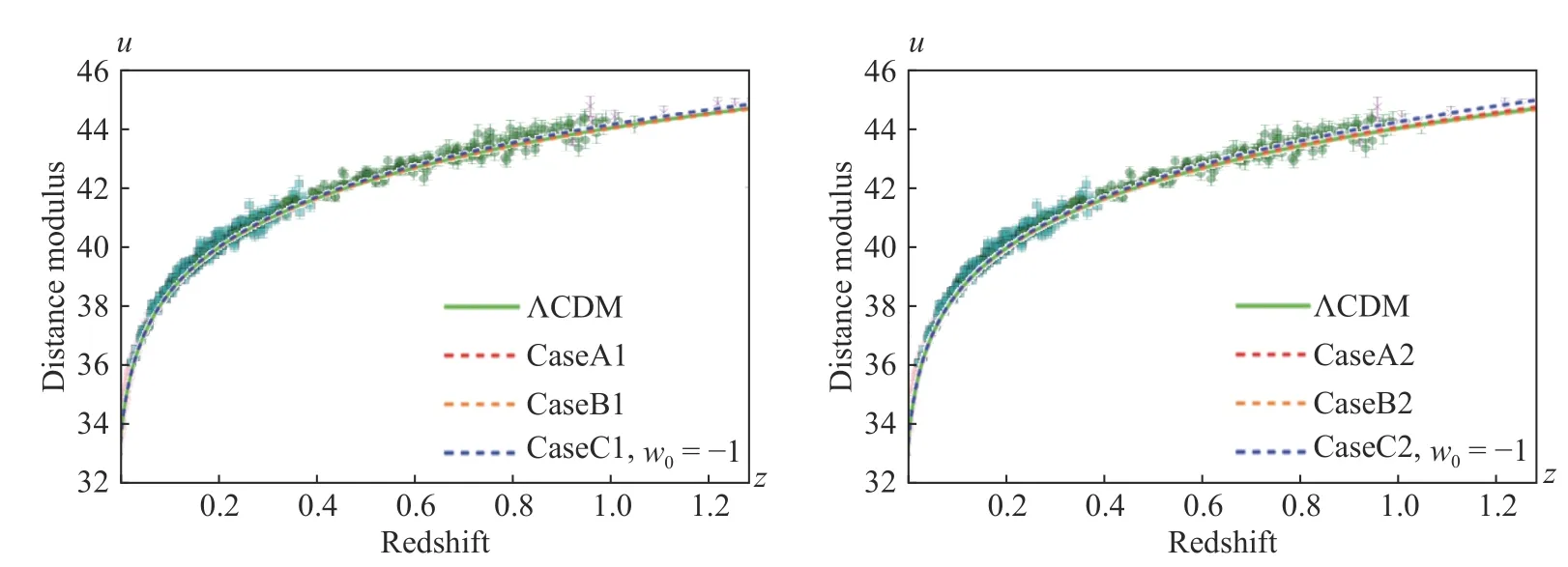
图9 K=+1,Λ0=−0.02Λ,a0H0=3.0 情况下, 距离模数的模型预言值与测量值的对比.Fig. 9 Comparison of the measured distance modulus with its expected value when K=+1,Λ0=−0.02Λ,a0H0=3.0

图10 K=+1,Λ0=−0.02Λ,a0H0=2.5 情况下, 距离模数的模型预言值与测量值的对比Fig. 10 Comparison of the measured distance modulus with its expected value when K=+1,Λ0=−0.02Λ,a0H0=2.5

ΛCDM模型中的ΩΛ、空间平坦的大尺度洛伦兹破缺模型中的Ωeff(K=0) 、空间不平坦的大尺度洛伦兹破缺模型中的Ωeff(K=±1)以及ΩK随着宇宙尺度因子的演化结果见图14, 其中大尺度洛伦兹破缺模型均以CaseA1为例.

从图14可以看到ΩΛ、Ωeff(K=0) 和Ωeff(K=±1) 的演化结果是相近的, 所以单纯从效果上看,它们的贡献是简并的.

图11 K=−1,Λ0=−0.02Λ,a0H0=3.5 情况下, 距离模数的模型预言值与测量值的对比Fig. 11 Comparison of the measured distance modulus with its expected value when K=−1,Λ0=−0.02Λ,a0H0=3.5

图12 K=+1,Λ0=−0.02Λ,a0H0=3.0 情况下, 距离模数的模型预言值与测量值的对比Fig. 12 Comparison of the measured distance modulus with its expected value when K=+1,Λ0=−0.02Λ,a0H0=3.0

图13 K=+1,Λ0=−0.02Λ,a0H0=2.5 情况下, 距离模数的模型预言值与测量值的对比Fig. 13 Comparison of the measured distance modulus with its expected value when K=+1,Λ0=−0.02Λ,a0H0=2.5

根据修正的Friedmann方程可以得到曲率密度 ΩK随着宇宙尺度因子的演化结果, 在K=+1 和K=−1这两种情况下, 曲率密度的演化见图15.

由此可以得到ΩK的最大值与最小值. 在K=+1的情况下, CaseC1具有最小的曲率密度ΩK=−0.34 ;在K=−1的情况下, CaseA1具有最大的曲率密度ΩK=0.6. 曲率密度的绝对值都是先增大, 在到达最大值后, 逐渐减小, 直至趋近于0. 曲率密度绝对值也可以参考图1—图3,H的演化是衰减的,a2H2在演化过程中具有最小值.

图14 K=+1,a0H0=3.5,Λ0=−0.02Λ 情况下, 3种模型之间的比较Fig. 14 Comparison of the three models whenK=+1,a0H0=3.5,Λ0=−0.02Λ

图15 K=+1,a0H0=2.5,Λ0=−0.072Λ情况下,ΩK 随尺度因子的演化Fig. 15 ΩK changes with the scale factor whenK=+1,a0H0=2.5,Λ0=−0.072Λ

在我们考虑的限制条件下, 根据修正的Friedmann方程可以得到a¨ 的演化, 也就是宇宙膨胀的加速度.K=+1和K=−1情况下,a¨ 随着宇宙尺度因子的演化见图16. 从图16可以粗略地得到, 在宇宙尺度因子为 0.5a0之前宇宙是减速膨胀的, 在此之后, 宇宙变为加速膨胀, 这与观测到的宇宙由减速膨胀变为加速膨胀是一致的, 从而进一步地加强了空间非平坦的大尺度洛伦兹破缺模型的可信度.

图16 随尺度因子的演化: a) K=+1,a0H0=3.5,Λ0=−0.02Λ ; b)K=−1,a0H0=3.5,Λ0=−0.02ΛFig. 16 changes with the scale factor: a) K=+1,a0H0=3.5,Λ0=−0.02Λ ;b)K=−1,a0H0=3.5,Λ0=−0.02Λ

3 总结与展望

导致高红移测量与低红移测量之间的H0紧张关系的原因迄今未知. 人们已经提出了很多解决H0紧张关系的方法. 有人提出是因为存在系统误差, 然而这些主张很快就被否定了[13-16]. 双中子星并合产生的引力波[17]或许能对H0进行独立的测量[18], 虽然未来的观测应该能够将误差减小[19-24]. 但是目前这种测量方法的误差较大(因为是单个事件), 因此并不能解决H0测量值之间的紧张关系. 此外, 作为ΛCDM 模型最简单的替代模型之一: 在非平坦的FRW宇宙中, 具有光滑势能的, 缓慢或者中等速度滚动的quintessence场, 被期望可以解决哈勃常数测量之间的紧张关系. 但是在结合了最新的CMB,SNe和BAO数据后发现, 这种模型并不能减缓哈勃常数的紧张关系[25].

在文献[26]中, 提出了基于Simsilum仿真与射线跟踪算法来解决H0测量值之间紧张关系的方法,由于宇宙结构的相对论性与非线性演化导致出现了空间曲率不为0的现象. 由此推断出的哈勃常数H0=(68.1±2.0)km/(s·Mpc)能够减缓CMB与距离阶梯之间的H0测量值之间的紧张关系. 因此, 导致空间曲率不为0的非线性相对论性演化能够缓解CMB与距离阶梯之间的H0测量值之间的紧张关系, 并且认为出现这种紧张关系是FLRW几何的刚性体现.

当前阶段, 空间曲率不为0似乎是解决哈勃常数问题的可行方法. 实际上, 我们也可以反而言之,低红移和高红移测量之间存在的紧张关系是空间曲率不为0的一个间接证据. 从天文观测的角度来看, 目前在低红移还没有对空间曲率进行直接测量(得到的约束也仅仅是将FLRW拟合到数据的结果, 这并不等价于直接测量).

总而言之, 虽然空间不平坦的大尺度洛伦兹破缺模型相较基于K0 的 ΛCDM 模型, 多出了一个宇宙学尺度上的contortion参量, 但是通过多种方式能够将各个输入值很好地限制在一定的范围内,并且在此范围内得到的距离模数、宇宙膨胀加速度等理论预言都能比较好地与观测结果吻合.

结合 CMB温度涨落功率谱, 利用 ΛCDM 模型可以严格限制各宇宙学参数. 同样地, 基于大尺度洛伦兹破缺模型, 结合当前的 CMB 数据, 也能够限制空间不平坦的大尺度洛伦兹破缺模型预言的哈勃常数, 再将其与基于 ΛCDM 模型 CMB得到的H0, 局域测量得到的H0比较分析来确定空间不平坦的大尺度洛伦兹破缺模型能否使H0测量问题得到改善. 具体计算需要借助类似Code for Anisotropies in the Microwave Background(CAMB)的计算软件包, 由 CMB 数据得到具体的宇宙学模型下的宇宙学参数值, 最新研究也指出H0的测量疑难[7]可能与空间平坦 ΛCDM 假定有关, 空间非平坦的宇宙可以是一个备选选项[8]. 本文研究了空间非平坦大尺度洛伦兹破缺模型中空间曲率密度受到的限制, 发现空间曲率非零与现有的观测是可以协调的, 这为利用空间曲率非零的宇宙学模型解决H0紧张关系提供了一个可行的前提. 我们拟在将空间曲率非零的大尺度洛伦兹破缺模型与 CMB 温度涨落功率谱结合,利用诸如CAMB之类的相关计算软件包计算相应的H0值, 在解决H0的紧张关系方面开展进一步的研究.