规则波跨越潜堤传播新型数值模型

2021-02-06张哲交通运输部天津水运工程科学研究所

珠江水运 2021年1期

◎ 张哲交通运输部天津水运工程科学研究所

近岸水域水体运动复杂多变，波浪作为重要的要素之一，一直是学者研究的热点。波浪自海上生成后，由深海向岸边进行传播，当传播至岸边时，由于水深变浅发生破碎。波浪破碎区域的水流会产生剧烈运动对海岸造成破坏，对近岸水域波浪传播进行研究具有重要的价值。目前业界研究的方法主要有三种：现场观测法、物理实验法和数值模拟法。现场观测法较为直观，数据最为真实可靠，但需长时间蹲守来获取足够数据，这在一定程度上加大了人力和物力的投入。物理模型法可以在按比例尺缩小的物理模型内开展研究，适于处理边界复杂和多维难题，但也有着变态影响、场地限制和可重复性差等缺点。数学模型研究与前两种方法相比无需投入大量的人力和物力，经济节约、可重复性高且不受场地条件限制，受到业界的广泛应用。

对规则波跨越潜堤传播进行数值模拟涉及干湿动边界的捕捉和波浪破碎的处理，基于有限差分方法求解Boussinesq方程，通常采用涡粘、水滚等方式人为引进可调参数近似处理，造成了不确定性。将有限体积法和有限差分法耦合求解Boussinesq方程可以规避上述不确定性。文章建立了基于限体积法和有限差分法耦合求解的一维Boussinesq水波模型，并对规则波在潜堤上的传播形态进行了模拟，吻合度良好。

1.数值模型

1.1 模型方程

Kim将Boussinesq方程推导为如下形式：

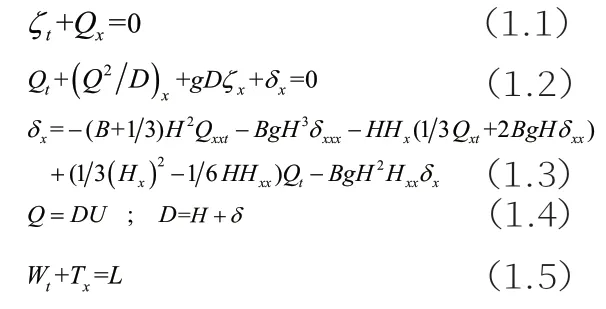
1.2 有限体积离散

有限体积法离散过程如下：

将公式（1.5）在单元体上求积分，运用散度定理转化方程，求得下式：

公式（1.6）中，Γ代表单元的边界；Ω代表求解的单元区域；nx则是单元体的外法向量。

对计算域进行空间、时间离散。空间上离散形式如下：

公式（1.7）中Δx为空间步长，N为水平方向网格数目，i代表网格编号。时间上离散形式为：

公式（1.8）中，Δt为时间步长，应用格林定理在有限体积[xi-1/2，xi+1/2]×[tn，tn+1]内对控制方程（1.5）进行积分，得到方程如下：

1.3 干湿动边界处理

采用薄层水体法处理干湿动边界，将0.001m水深作为阀值，即网格处若水深大于0.001m视为水域，网格处若水深小于0.0 01m视为陆地，并将陆地水深赋值为0.001m，流速取零。

1.4 边界条件

在计算域左端设置三个虚拟网格：-3、-2、-1，计算域右端同样设置三个虚拟网格：N+1、N+2、N+3，分别按照下式取变量值：

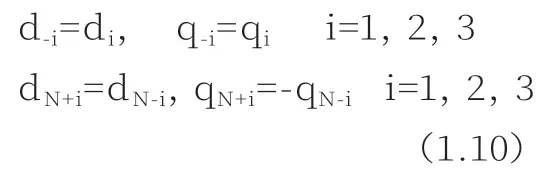
将源项引入质量方程中产生波浪，为吸收计算域两端的波浪采用设置海绵层法，每一时间步的数值解乘以光滑函数 f(x)。f(x)中xs为海绵层长度，取1.5倍波长。

采用CFL稳定性条件保证计算收敛：

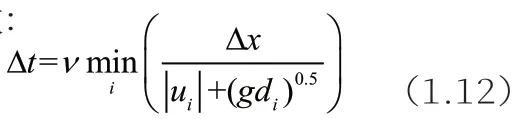
公式（1.12）中v=0.5。

1.5 时间积分方法

采用三阶龙格-库塔方法进行时间积分：

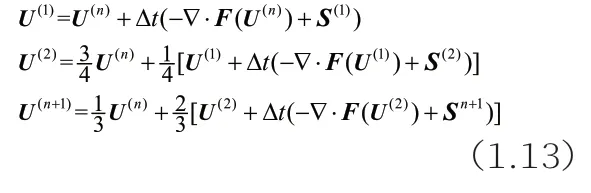
2.数值验证

选取Luth et al.的规则波在潜堤上传播的物理实验验证本文数值模型，图1给出了实验地形。图2中曲线为本文模型模拟数值，圆圈为实验数据。图中可以看出，波浪未传播至潜堤时，传播速度恒定，波幅和形状恒定不变。波浪到达潜堤前坡时，水深减小，在浅化作用下波高变大，产生高次谐波，波谷逐渐趋于平坦，非线性增强。波浪越过潜堤的顶面后，到达潜堤后面的常水深位置后非线性变小，谐波在非线性作用下锁相波变化成了自由波。由图可知，数值模拟结果与实验数据高度拟合。验证了本文建立的数值模型适用于波浪在复杂地形上传播的模拟。