基于多目标可靠性优化平台的车身前部结构设计＊

高丰岭 燕唐 战楠 卜晓兵

（中汽研汽车检验中心（天津）有限公司，天津 300300）

主题词：多目标可靠性优化 车身结构优化 序列更新代理模型 概率充分因子

1 前言

车身研发是复杂的系统问题，需要考虑包括结构耐撞性，静、动态力学特性及轻量化水平等多种因素。与仅提供1个最优解的单目标优化相比，多目标优化在车身设计中更常用，其可为设计人员提供由一系列折衷方案组成的帕累托最优前沿（Pareto Optimal Front，POF），以便后续决策[1]。

在实际工程问题中，制造公差、载荷条件、材料特性、几何结构等存在一定程度的不确定性[2]，为了避免执行确定性多目标优化时得到实际不可靠、不可行的设计方案，考虑上述不确定性因素开展车身结构多目标可靠性优化设计十分必要。国内外学者在此方面开展了大量的研究工作。Shetty 和Nilsson[3]对B 柱总成的侧面耐撞性设计进行了研究，比较了多目标确定性、可靠性和鲁棒性优化结果。Duan 等人[4]提出了一种改进的多目标可靠性优化方法，并应用于概念车身设计。Lv 等人[5-6]分别实现了汽车前端和保险杠系统的多目标可靠性优化。在这些研究中，代理模型在提升优化效率方面起到了重要作用，但代理模型的构造更多凭借工程经验，如何兼顾优化精度与效率仍需深入研究。

改善代理模型从而保证优化精度的方法通常有2种[7]。一种是一步构造高质量代理模型。这种方法思路直接、流程简单，在工程上广为应用，但往往需要在整个设计域内大量采样以增加其在真实解邻域内出现的概率从而满足精度要求，难以平衡优化精度与效率。另一种为序列更新代理模型。其利用本次迭代得到的优化结果生成补充样本点，进而不断提高优化精度逐步逼近真实解。由于初始样本点数量较少，后续补点可控，因此该类方法在整体优化效率方面较前者更好。尽管该类方法具有广阔的应用前景，但基于其开展车身结构多目标可靠性优化仍然存在一些挑战，比如可靠性约束的处理、优化算法的选择以及补点策略的制定等较难统筹，因而在不损失优化精度的基础上保证整体优化效率存在困难。

鉴于此，本文集成概率充分因子法、自适应加权多目标优化算法、径向基函数代理模型以及自适应补点方法，构建基于序列更新代理模型技术的车身结构多目标可靠性优化平台，并对其进行测试和应用。

2 多目标可靠性优化平台

多目标可靠性优化的数学表达式为：

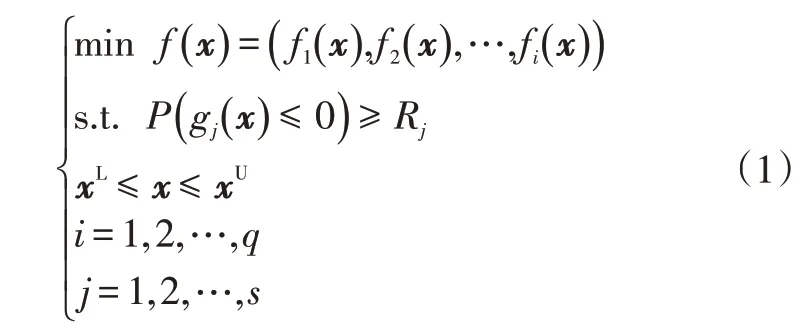
式中，fi(x)、gj(x)分别为第i个设计目标和第j个确定性设计约束；x为具有一定分布特征的设计变量向量；xL、xU分别为x的下限和上限；P()为以Rj为目标可靠度的概率约束；q为设计目标总数；s为约束总数。

通过适当的概率约束处理，将可靠性优化问题转化为确定性优化问题，利用代理模型代替耗时的仿真模型并持续更新模型提升精度，采用高效多目标优化求解器，即可求解得到高精度近似POF。建立的多目标可靠性优化平台计算流程如图1所示。

2.1 径向基函数代理模型

由于对非线性物理模型具有良好的描述能力，同时对离散多变量数据进行插值的能力较强，径向基函数（Radial Basis Function，RBF）模型在工程界与学术界都受到了高度重视。通常，RBF模型分为数量为m的径向基函数和数量为n的带加权系数的多项式项，其数学表达式为：

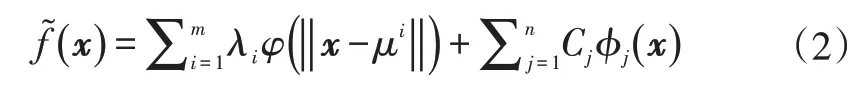
式中，‖x-μi‖为设计点x与观测输入μi之间的欧几里德距离；φ为径向基函数；λi为未知权重因子；φj(x)为多项式项；Cj为系数。

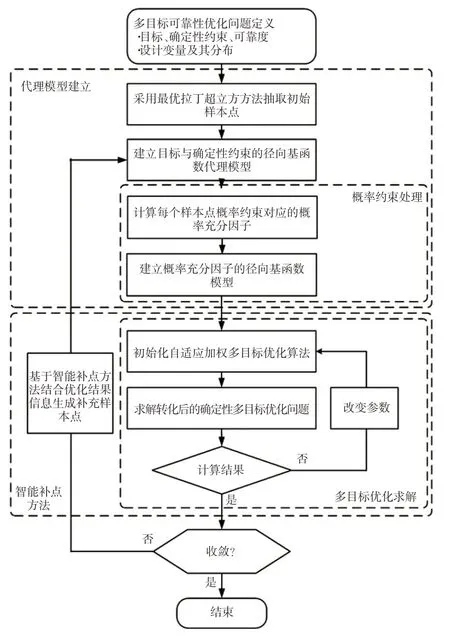
图1 多目标可靠性优化平台计算流程

2.2 概率充分因子法

通过将安全因子与蒙特卡洛仿真得到的失效概率相结合，概率充分因子（Probabilistic Sufficiency Factor，PSF）法可以在仅增加一小部分计算量的条件下足够精确地处理可靠性优化问题[8-10]。基于概率充分因子法，式（1）中相应的概率约束可替换为：

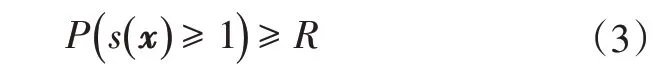
式中，s(x)为由确定性约束的上界或下界与其在优化过程中计算的实际响应之比决定的安全系数；R为Rj的集合。

概率充分因子V是可靠性水平大于或等于R的安全系数，因此，式（3）可以进一步改写为：

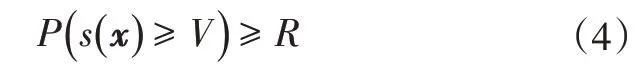
在蒙特卡洛仿真基础上，V可由式（5）计算得出：

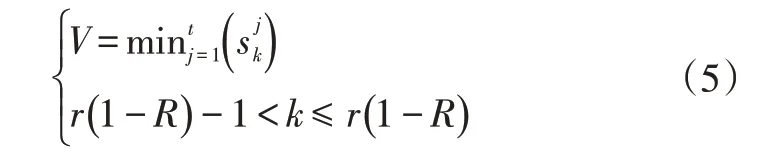
当V≥1 时，可靠性水平等于或高于目标值，因此设计方案满足规定的安全要求；当V＜1 时，设计方案不满足安全要求。此外，在优化过程中，V可以用代理模型估算。

2.3 自适应加权多目标优化算法

为了克服进化类算法计算效率低、传统基于梯度信息的加权算法在非凸区域解分布不均或者无解的缺点，Kim 等人提出了一种自适应加权多目标优化算法[11-12]。其基本思想是在传统加权算法得到初始POF的基础上，通过增加额外约束并进行子优化的方式在分布不均匀的初始POF 上寻找未知区域的非支配解。优化求解流程如图2所示。

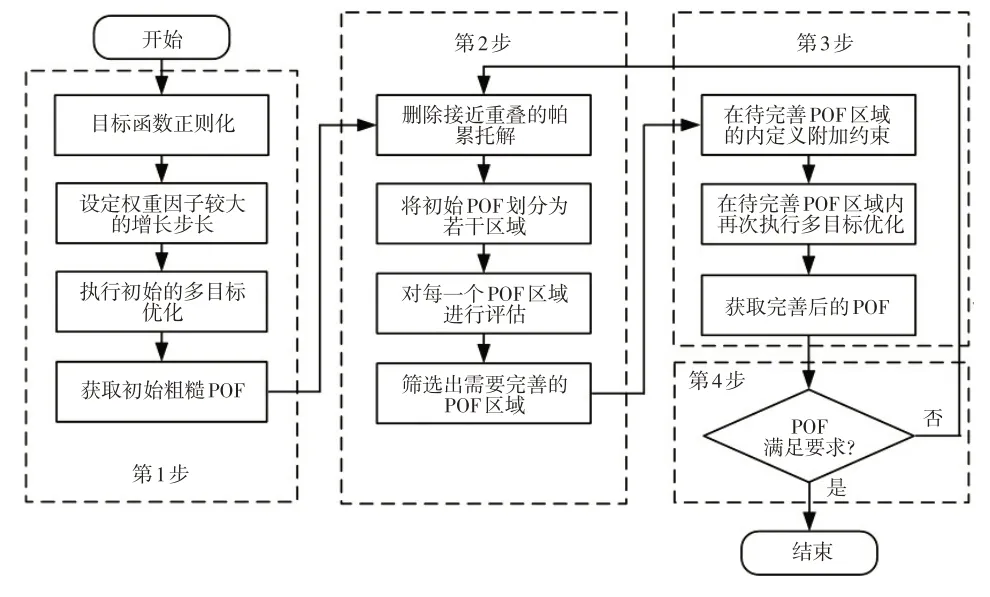
图2 自适应加权多目标优化算法流程

2.4 智能补点方法

为了保证最终近似POF的精度，本文引入智能补点方法来序列更新RBF模型。智能补点方法基于本次优化所得POF的极值点、最大、最小距离点以及设计域边界等信息插值生成补充样本点[13]，其详细流程如图3所示。

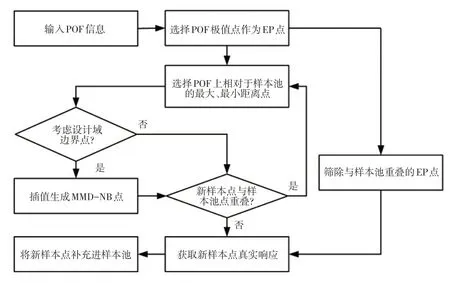
图3 智能补点方法流程[13]

2.5 收敛准则

阈值η的默认值为20%，当优化结果满足式（6）时算法收敛：

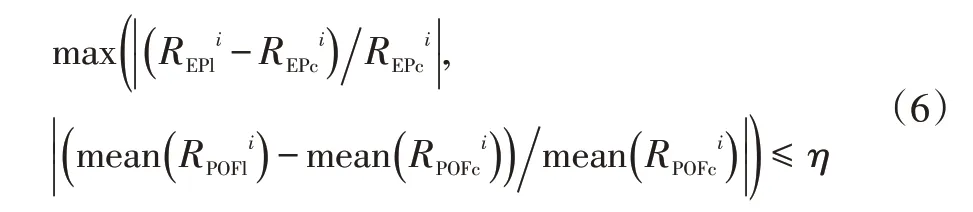
式中，REPli、REPci、RPOFli、RPOFci分别为第i个设计目标上次和本次迭代得到的POF 极值点、上次和本次迭代得到的POF点。

3 数值算例

本文通过工字梁设计算例对建立的多目标可靠性优化平台性能进行验证。如图4所示，工字梁的设计要求为在2 个给定力的作用下，梁的垂直挠度最小，以梁的截面积和几何尺寸作为设计变量，同时要满足应力约束。这里设计变量均服从正态分布，作为输入的不确定性因素。

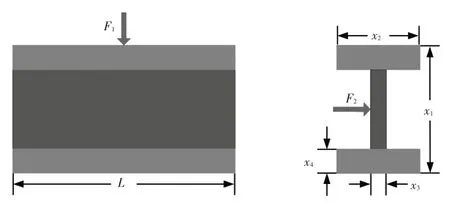
图4 工字梁设计问题

该问题的相关参数为：梁的容许弯曲应力为60 MPa，杨氏模量为0.2 GPa，最大弯曲力F1=600 kN、F2=50 kN，梁的长度为L=200 cm。

无量纲化处理后，该确定性多目标优化问题可以表述为：

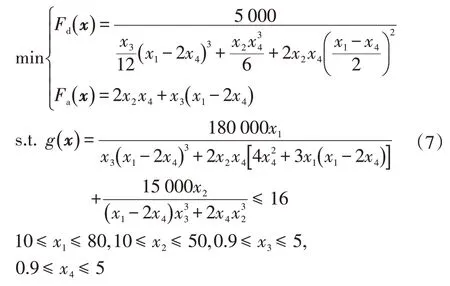
式中，Fd(x)、Fa(x)分别为该工字梁的垂直挠度和横截面积；g(x)为梁在上述工况下的应力约束；x=[x1,x2,x3,x4]为尺寸设计变量，具体见图4。

将应力约束可靠度及设计变量变异系数分别设为99%和10%，建立与式（7）对应的工字梁多目标可靠性优化数学模型：

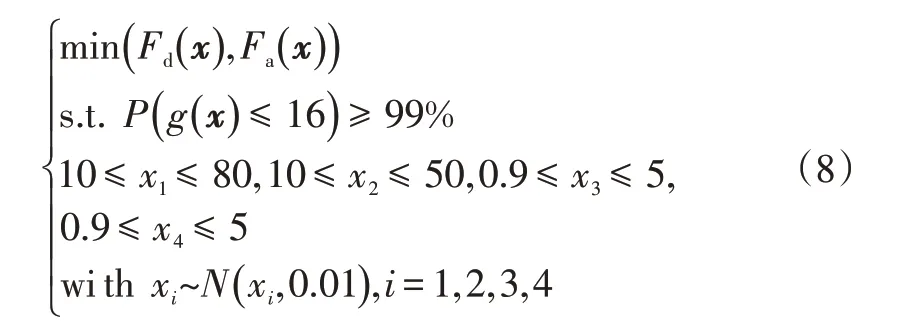
根据概率充分因子方法，可将该梁设计问题的多目标可靠性优化模型进一步转化为：

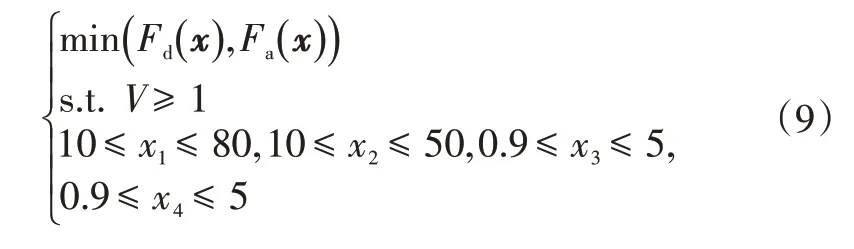
为对比分析，首先采用最优拉丁超立方方法抽取30个初始样本点，经过5次迭代后，算法收敛，共增加10个新样本点。图5给出了近似POF的逼近过程，由于最终近似POF 与真实POF 的一致性良好（除了上端部），该优化平台的有效性得到了证明。

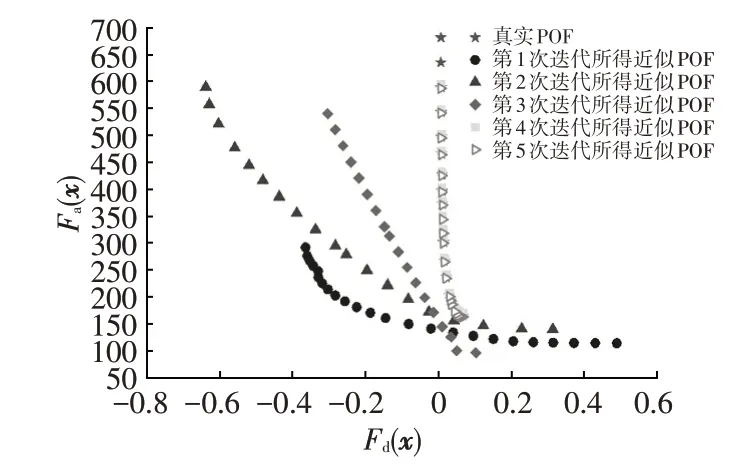
图5 近似POF的逼近过程

除提出的优化平台（方法1）外，为了深入比较研究，采用另外2 种方法求解该设计问题，包括标准的基于代理模型的PSF方法[14]（方法2）和工程中常用的安全系数法（方法3）。在方法2 和方法3 中，采用最优拉丁超立方方法生成50 个样本点一步构造RBF 模型，选择多目标粒子群算法作为求解器，考虑到算法的精度，将多目标粒子群算法中的种群大小和最大迭代次数均设置为100。此外，方法3中的安全系数设为1.2。

3 种方法的优化结果如表1 所示，与另外2 种方法相比，提出的优化平台在控制样本点数量及提高算法效率方面都具有一定优势。图6给出了3种方法所得近似POF 与真实POF 的对比结果。3 种方法所得近似POF的左侧部分与真实POF高度一致，因此可以满足可靠度R≥99%的设计要求。其右侧部分，尽管方法1 和方法2的Pareto解精度并不十分理想，但与真实POF的误差相对较小。因此，该优化平台能够平衡优化精度与效率之间的关系，可以在结构优化领域有效应用。

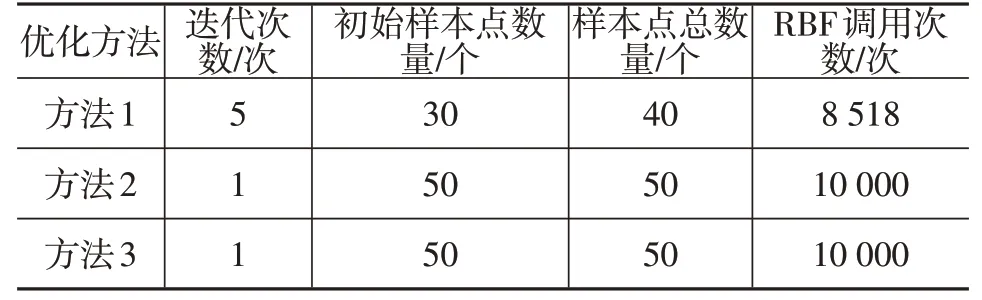
表1 3种方法的优化结果

4 白车身性能仿真分析

4.1 白车身有限元建模

对某款纯电动汽车的全承载式白车身进行设计，电池包位于该车身下部。以2D壳单元为主建立白车身有限元模型，如图7所示。模型中的材料以Q235钢为主，采用线弹性各向同性材料模型进行模态与刚度分析，采用分段线性塑性材料模型进行耐撞性分析。

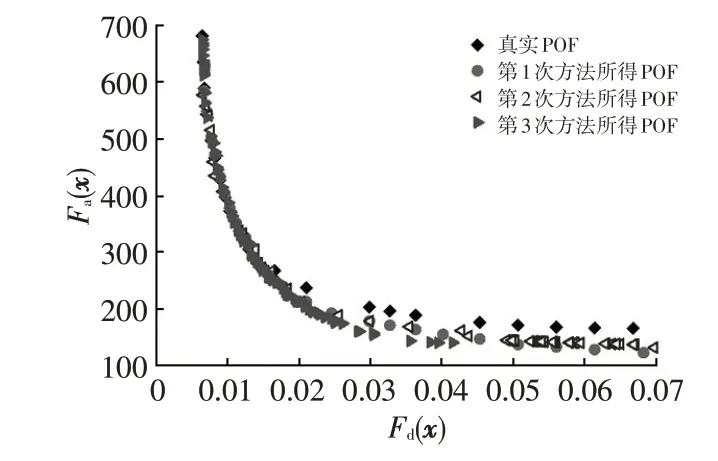
图6 3种优化方法所得POF与真实POF的对比

图7 白车身有限元模型

4.2 模态分析

基于Lanczos方法，计算了白车身前6阶固有频率，其值与相应的振型如表2 所示。较高的车身基频（1 阶模态频率）可以有效降低来自路面的加速度冲击，而对于乘用车，基频通常需要达到18～32 Hz 的范围。初始设计的白车身基频为26.24 Hz，基本满足要求。

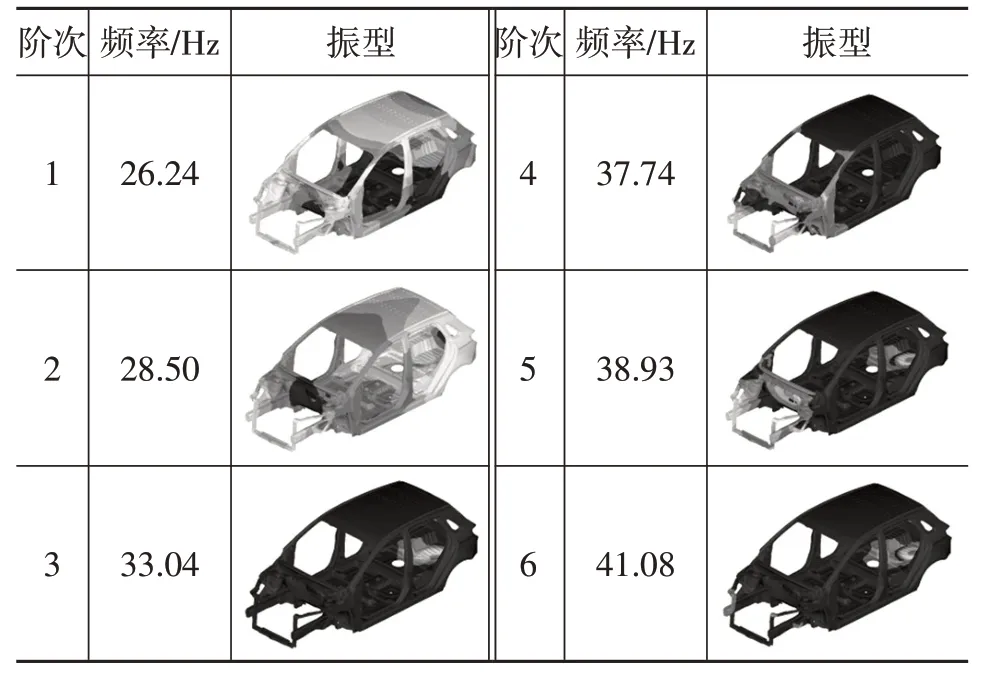
表2 白车身前6阶固有频率及振型

4.3 刚度分析

通过在白车身有限元模型上施加集中（F1～F4）与均布载荷（P1～P3），并限制前、后4个悬架连接位置的所有自由度，建立了弯曲刚度分析工况，如图8所示，表3给出了弯曲工况相关参数。

扭转刚度分析工况如图9 所示，边界条件定义为：在前轴的悬架减震塔处作用一对沿Z轴方向相反的力|FT|=5.89 kN，约束前轴中点Y轴和Z轴上的平动自由度及旋转自由度，其他边界条件与弯曲刚度工况一致。

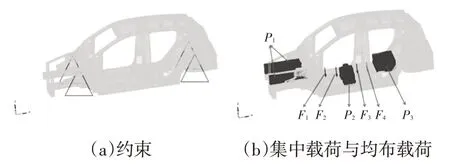
图8 弯曲刚度工况边界条件

表3 弯曲刚度载荷

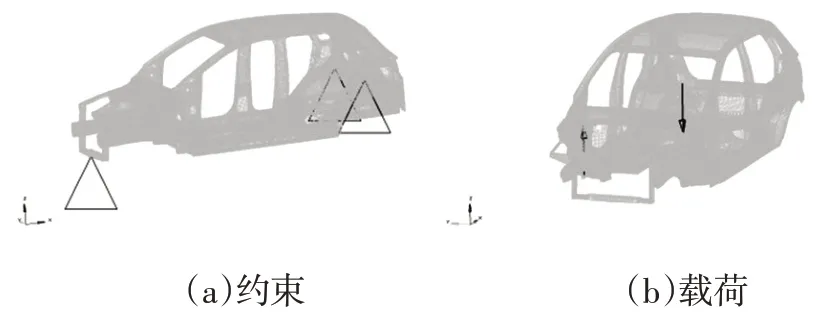
图9 扭转刚度工况边界条件

为了计算白车身的弯曲、扭转刚度，在有限元模型上定义了一系列观测点，如图10所示。

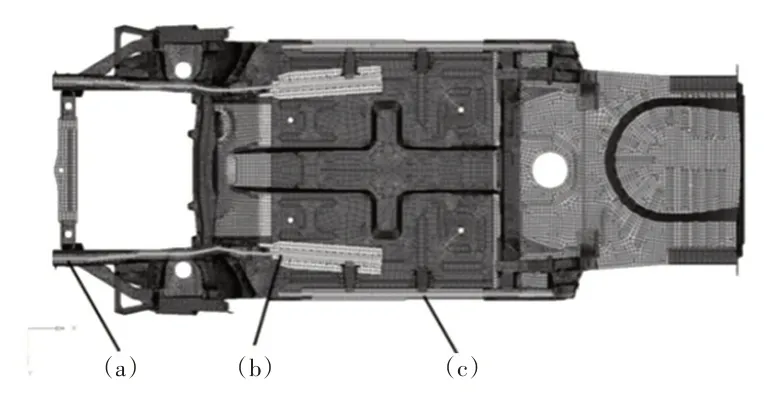
图10 白车身刚度计算观测点

白车身弯曲刚度KB、扭转刚度KT计算公式为：

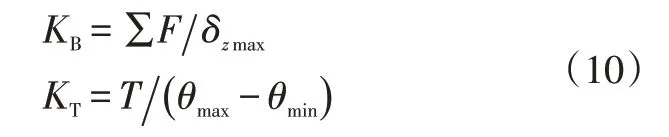
其中，ΣF为表1 中所列载荷总和；δzmax为观测点的最大弯曲挠度；T为作用在前轴上的扭矩；θmax、θmin分别为由观测点得到的车身最大、最小扭转角。

计算可得，KB=5 545.8 N/mm，KT=5 021.0 N·m/(°)。

4.4 100%重叠正碰耐撞性分析

由于该工况下白车身变形主要集中在前部，为了提高效率，仅保留前部车身结构，在车辆质心位置定义质量点代替与前端刚性连接的乘员舱及后部模型，简化处理后的仿真模型如图11所示。碰撞初速度设为50 km/h，碰撞仿真时间为25 ms。计算可得总吸能与最大碰撞力分别为15.27 kJ和417.18 kN。

5 前部车身结构多目标可靠性优化

5.1 优化问题定义

考虑到对白车身整体性能的巨大贡献，对车身前部结构进行优化设计。鉴于电动汽车节能与安全的重要性，以正碰吸能量以及前部车身结构质量为设计目标，而最大碰撞力、基频、弯曲刚度、扭转刚度均不能低于初始设计水平。定义5 个部件厚度作为设计变量，如表4所示，考虑部件制造公差为不确定因素，设计变量服从正态分布，变异系数为10%。

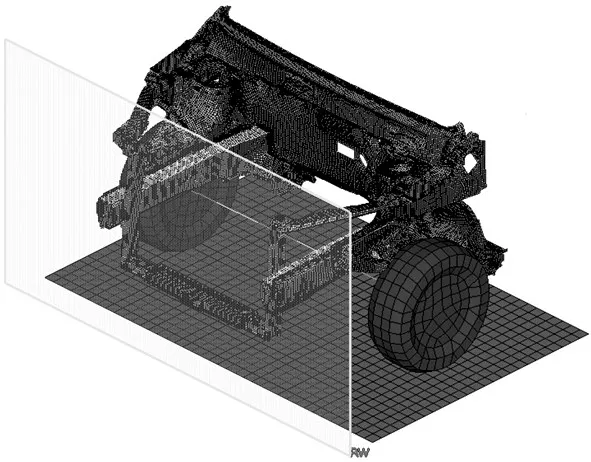
图11 简化后的正碰模型

前部车身结构的确定性多目标优化数学模型为：

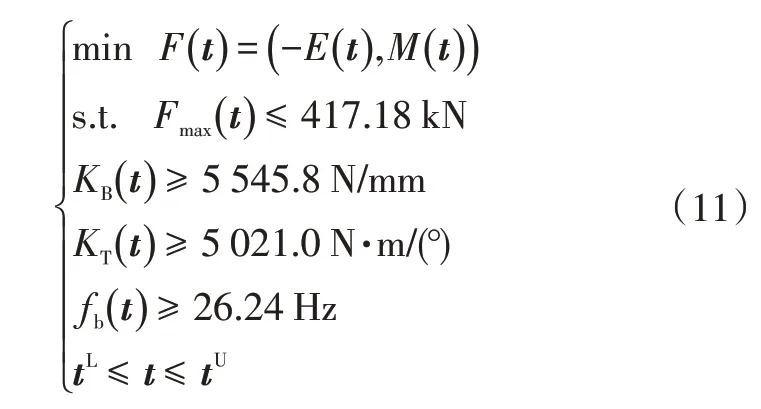
式中，t=[t1,t2,t3,t4,t5]为设计变量；tL、tU分别为t的下限和上限；E(t)、M(t)、Fmax(t)、fb(t)、KB(t)及KT(t)分别为吸能量、质量、最大碰撞力、基频、弯曲刚度及扭转刚度。

相应的多目标可靠性优化数学模型为：

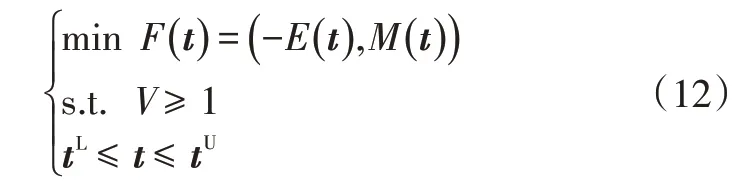
5.2 结果与分析

基于优化平台，采用最优拉丁超立方方法抽取30个初始样本点，经过4次迭代后优化收敛，共生成7个补充样本点。最终的近似POF 包含了20 个备选设计方案，如表5所示。从表5中可知，尽管有3个解没能满足设计要求（V≥1），但其值已经十分接近1，满足工程需要。图12 给出了近似POF 的迭代过程，可以看出车身前部吸能量与质量相互制约，如果倾向于提高吸能量，则最终POF 左上部分的解（表5 中序号较大者）可作为备选方案，如果倾向于轻量化，则最终POF 右下部分的解（表5 中序号较小者）可作为备选方案。考虑到前部车身的综合性能，这里选择质量相对较轻，力学性能均优于初始设计的第18 个Pareto 解作为最终设计方案。如表6所示，由于与对应的有限元仿真结果相比误差可被接受，所以优化精度满足要求。

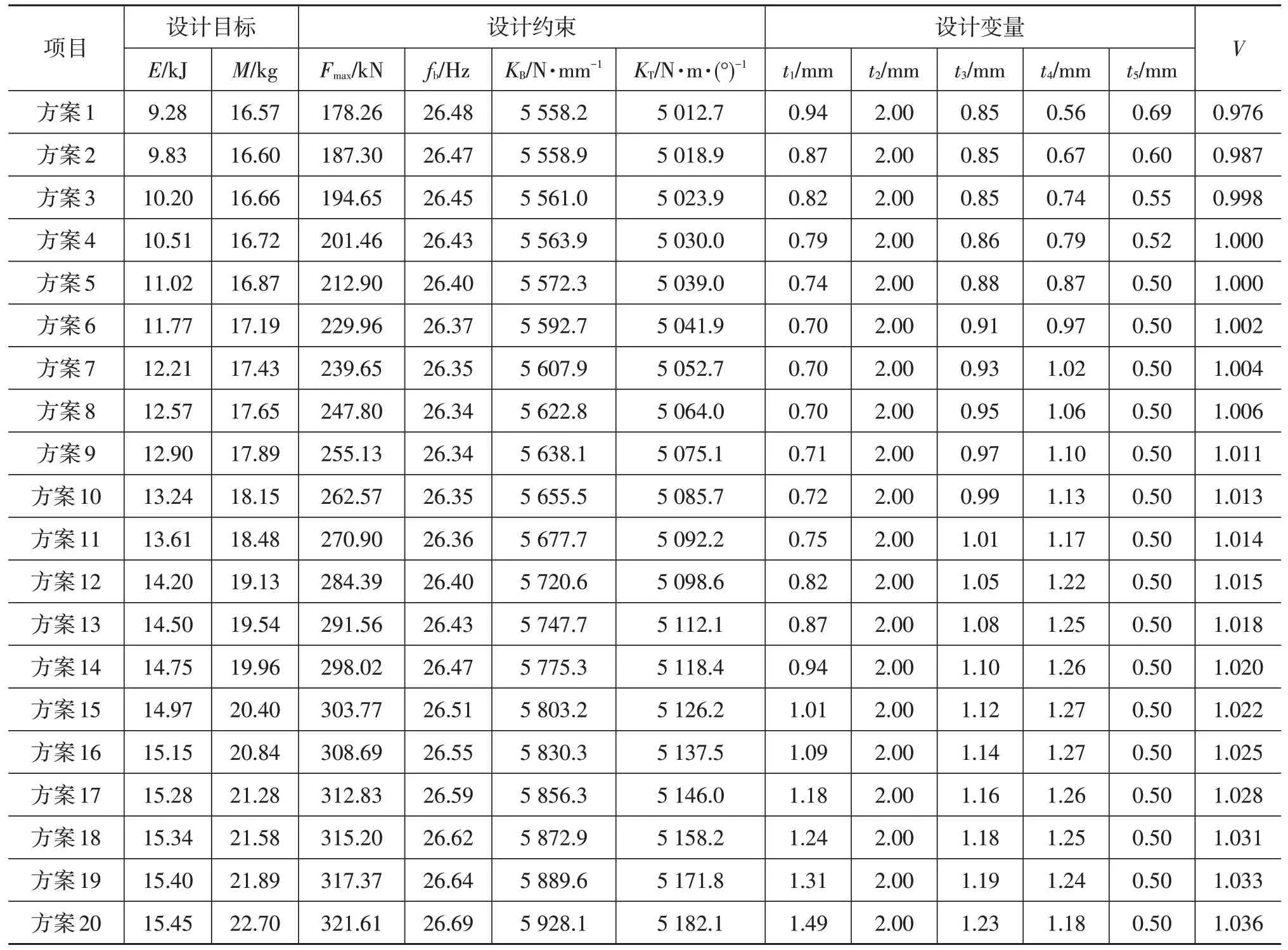
表5 最终近似POF中的备选设计方案

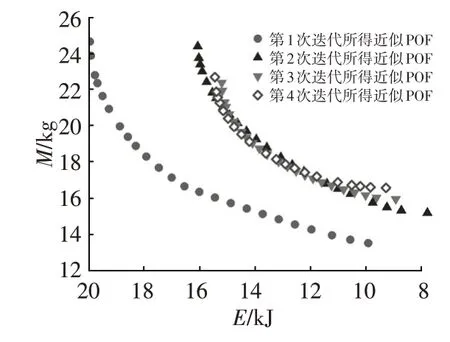
图12 近似POF迭代过程

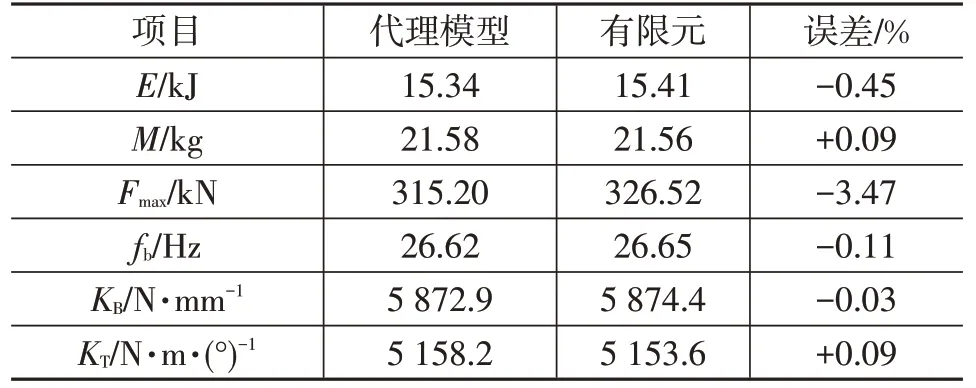
表6 最终近似POF中的备选设计方案

6 结束语

本文基于RBF 代理模型、概率充分因子方法、自适应加权多目标优化算法及智能补点方法建立了一个车身结构多目标可靠性优化平台。以工字梁设计问题为数值算例，对优化平台的实际应用效果进行了验证。通过与一步建立径向基函数模型的概率充分因子方法及安全系数法对比分析，证明了优化平台在保证近似POF精度可接受的同时，在样本量控制和计算效率方面具有一定优势。

最后，考虑模态、弯曲与扭转刚度、正碰耐撞性及轻量化水平等性能，应用优化平台对某款白车身前部结构开展了优化设计。最终的优化方案在保证前部车身结构吸能量提升的同时降低了质量，并满足可靠度要求。