内燃机歧管多分支动量守恒边界模型研究
2021-02-05王映远胡志龙邓康耀钱跃华
王映远,胡志龙,张 琨,邓康耀,钱跃华,刘 博
(1.上海交通大学 动力机械及工程教育部重点实验室,上海 200240;2.中国船舶集团有限公司第七一一研究所,上海 201108;3.中船动力研究院有限公司,上海 200120)
0 概述
船舶内燃机增压系统中排气气流能量在排气多分支接头的传递和转换是影响增压效果的重要因素[1-2]。随着内燃机功率密度的提升和转速范围的拓展,对其动力性、经济性、响应性的要求也进一步提高。特别是近些年来内燃机的增压程度不断提高,排气管系中的气体流速不断增大,气体压缩性对流经歧管多分支气流的压力损失影响越来越大[3],但现有歧管多分支模型以不可压缩流模型为主,模型的适用性和计算精度越来越难以满足内燃机增压系统设计技术体系的要求。为此,建立较高精度的排气管系多分支边界模型对提高内燃机一维循环仿真精度具有重要意义。
目前针对进排气歧管多分支边界模型研究以不可压缩流模型为主,可压缩流模型开发起步较晚。较早出现的歧管多分支模型为文献[4]中提出的等压边界模型,该模型对于歧管分支数大于3的结构有较好的适用性,但是该模型不能体现出歧管多分支夹角等结构参数对流动的影响,模型精度较低。为了提高歧管多分支边界模型的仿真精度,出现基于经验系数的压力损失模型,如文献[5-7]中分别基于稳态试验获得压力损失系数,拟合出不同结构和不同流动参数对压力损失的影响表达式。基于经验系数的压力损失模型对确定的结构获得结果比较便捷,但受试验条件限制使得研究对象比较单一。为了能够拓展压力损失模型的应用范围,基于理论推导的压力损失模型得到发展,具有代表性的是Winerbone压力损失模型[8-11]及在此基础上发展的模型[12-14]。基于理论推导的压力损失模型考虑了夹角、面积比等结构参数和流量比等流动参数对压力损失系数的影响,模型通用性较好,但是模型基于分支接头不可压缩流的流动,未考虑气体压缩性的影响;并且模型结构形式多以斜T型为主,只有3个分支,对于具有更多分支的结构形式没有进行更进一步的研究。文献[15-17]中提出了新的可以表征T型管接头绝热可压缩流的压力损失系数模型。该模型考虑了气体可压缩性的影响,但其适用性具有较大局限性,无法用于90°的T型管接头以外的多分支流动边界计算。
本文中基于动量守恒方程,考虑多分支歧管结构参数和工质压缩性的影响,推导出适用于任意分支数的动量守恒边界模型,并搭建瞬态仿真激波管算例和内燃机整机循环仿真模型,对比分析歧管多分支动量守恒边界模型与传统边界模型预测的精确度。
1 模型建立
1.1 模型假设
由于多分支歧管内部流动较为复杂,且流动状态存在多种不确定性,为了在歧管汇合区域即控制体内建立动量方程,作以下假设:(1) 歧管汇合区域内部流动绝热,流动过程无摩擦;(2) 各分支经过汇合区域进出口为单向流动;(3) 在某一时刻仅有一个端口为流入或流出,该支管定义为总管(com);(4) 接头内部流径流动满足分界流线假设,且各流径间只有动量交换,无能量和质量交换。
根据假设条件(3),建立了分散流和汇合流两种多分支接头流动形式,如图1所示。对于不同的流动类型,其对应的边界控制体动量方程也不同,应分别推导建立控制方程。

图1 多分支接头流动形式示意图
1.2 基本方程
多分支边界计算采用特征线的处理方法,需引入带星号的黎曼变量,动量守恒边界模型的连续性方程(式(1))和能量方程与等压边界模型相同[11]。
(1)
式中,下标j为端口号;F为端口截面积;AA为熵值的无量纲量;A为无量纲音速;U为无量纲速度;γ为绝热指数。带星号的黎曼变量定义为:
(2)
(3)
非等熵流动流过歧管多分支时有能量损失,因此对能量方程提出以下假设:当分支中的流体流入交汇区域(U*>0)时,其流体熵值不变,等于来流的熵值;流入汇合区域的流体在交汇区域充分混合后从流出端口流出,因此当分支中的流体为从交汇区域流出(U*<0)时,其流体熵值改变,其值等于流入接头总熵值的流量加权平均值。
(AAj)joining=AAj
(4)
(5)
式中,(AAj)joining为从支管j与交汇区域连接截面处流入的熵值;(AAj)separating为从交汇区域与支管j连接截面处流出的熵值;N为分支接头端口数。
1.3 动量方程建立补充方程
内燃机歧管多分支动量守恒边界模型计算需要先确定求解变量、已知变量、已建立方程与待建立边界方程。对于端口为N的多分支接头,当边界模型采用特征线方法时,需要确定3N个边界特征值。根据边界特征值的基本理论,流入歧管的端口有2个特征值为已知,流出歧管的端口有1个特征值为已知,则分散流和汇合流的已知特征值数分别为N+1和2N-1。接头边界处可建立1个连续性方程,分散流可建立N-1个能量方程,汇合流可建立1个能量方程。因此,为建立多分支歧管封闭的边界方程组,两种流型需要补充N-1个边界方程。

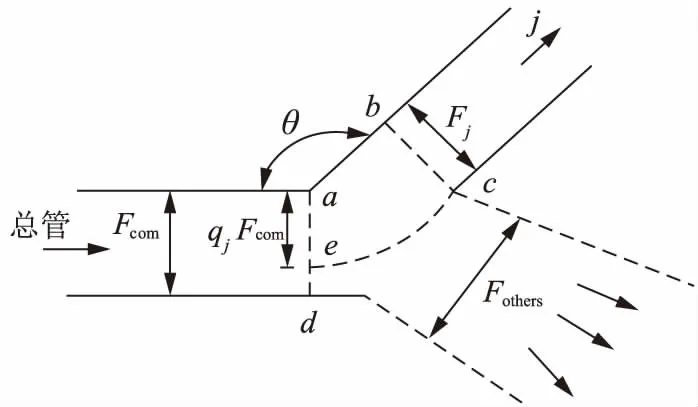
图2 多分支分散流流径控制体示意图
根据分界流线假设,总管流入支管j的通流面积与支管与总管的流量比相关,为qjFcom,其a-b-c-e区域与其他支管的边界控制体有动量交换而无能量交换。以边界控制体a-b-c-e区域为研究对象,沿支管j方向建立动量方程为:
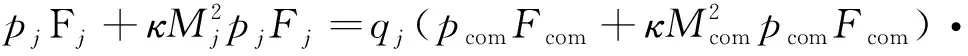
(6)
式中,pj和pcom分别为支管j和总管的压力;Mj和Mcom分别为支管j和总管的马赫数;κ为比热容比;pe-c为分界流线e-c对控制体的作用力平均值,该值可近似为e点和c点压力的平均值,即:
(7)
e点压力为总管来流压力pcom,c点压力近似为总管流体流动的滞止压力p0,com,即:
pe=pcom
(8)
pc=p0,com
(9)
将式(7)~式(9)代入式(6)可得:
(10)
式(9)为分散流任意支管j与总管流径控制体建立的边界动量方程。依次对所有流出端口与总管的流径建立相应的动量方程,可实现对多分支分散流边界相关参数的封闭求解。
图3为多分支汇合总管与任意支管j的流径示意图。根据假设条件(4),a-d截面为总管接头区域流出的总通流截面,流出支管j的工质由b-c截面流入接头,从a-e截面流出接头区域,该流径与其他支管(当量面积为Fothers)的流线分界线为e-c,则a-b-c-e

图3 多分支汇合流流径控制体示意图
区域为多分支汇合流支管j的边界控制体,针对该区域建立动量方程。
与分散流的分析过程相似,根据分界流线假设,支管j流入总管的通流面积与支管与总管的流量比相关,为qjFcom,其a-b-c-e区域与其他支管的边界控制体有动量交换而无能量交换。以边界控制体a-b-c-e区域为研究对象,沿支管j方向建立动量方程为:
cos(π-θ)+pe-c[Fj-qjFcomcos(π-θ)]
(11)
式(11)方程形式与分散流一致,但分界流线平均作用力pe-c的求解方法不同,对于汇合流e点压力为总管的压力,c点为支管j来流压力,即:
pe=pcom
(12)
pc=pj
(13)
将式(12)和式(13)代入式(11)可得:
(14)
式(14)为汇合流任意支管j与总管流径控制体建立的边界动量方程。依次对所有流入端口与总管的流径建立相应的动量方程,可实现对多分支汇合流边界相关参数的封闭求解。
2 模型验证与对比
上述推导过程是基于多分支展开的,因此动量守恒模型可以适用于任意分支数的结构。考虑三分支是多分支的一个特例,并且在实际应用中较为广泛,本文中选用三分支作为验证算例。文献[18]中开展了激波流经多分支的试验研究[18],如图4所示,可以借鉴该试验结果,建立相同算例,验证不同多分支模型预测的准确性和计算效率。图中,p1、p2、p3分别为测点1、2、3的压力。
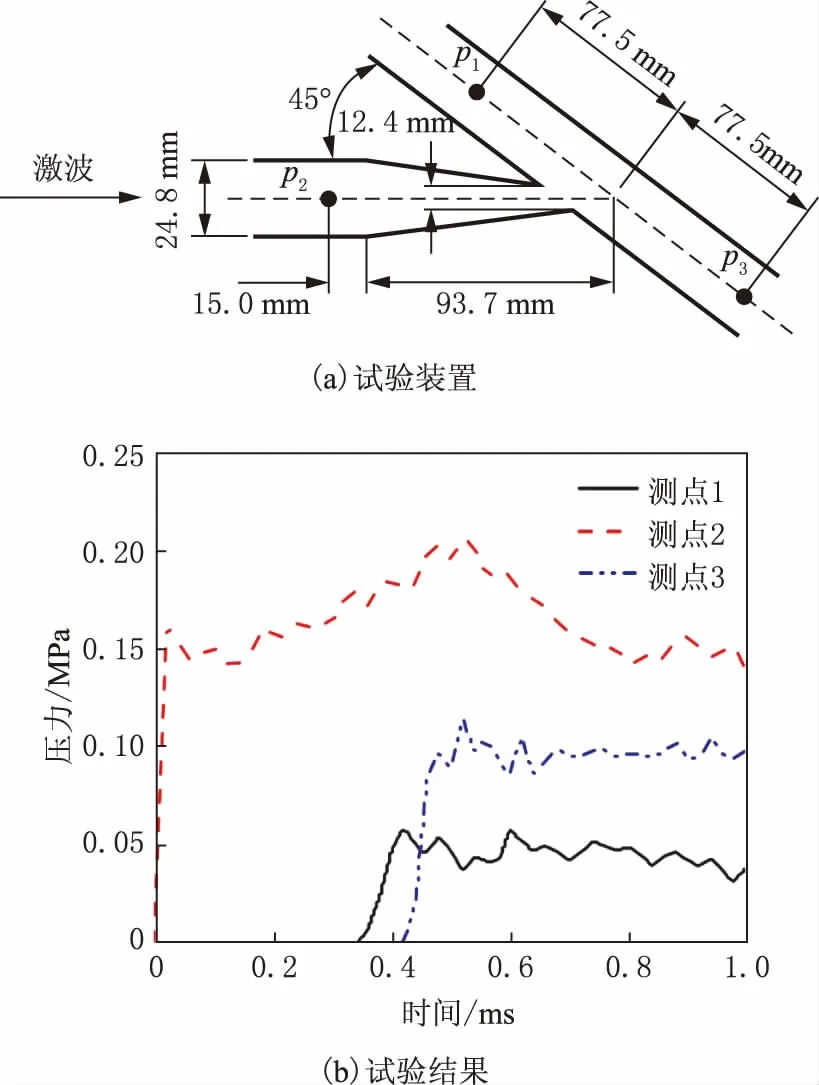
图4 文献[18]中试验装置及针对三分支开展的试验结果
该测试算例由1个多分支接头组件(管接头)、3个管道组件(管道1、管道2、管道3)和3个开口环境组件(环境1、环境2、环境3)组成。三分支组件夹角45°,各分支管结构参数如图5所示。管道组件管长为1.0 m,其中管道2为激波管,靠近环境2的 0.5 m 为高压端,靠近管接头的0.5 m为低压段,各组件初值参数在表1中已列出。激波管管道2的测试初值示意图如图6所示。

图5 三分支模型测试算例

图6 激波管管道2测试初值

表1 各组件测试初值参数
仿真时间为2 ms,管道离散尺度均为10 mm,管道组件计算采用二阶TVD格式,三分支分别选用Benson的等压模型、Winterbone的压力损失模型及本文建立的动量守恒模型。按照图4中标注的距离设置测点输出压力波结果,对比分析各测点不同模型激波流经后的压力变化。
2.1 仿真精度对比
图7为不同多分支模型预测结果与试验结果对比,压力波到达测点2为0时刻,对比1 ms时间内各测点的压力值变化。测点2由于未经过三分支交汇区域,等压模型和动量守恒模型和压力损失系数模型所预测压力波基本一致。压力波到达测点1后压力值迅速上升,随后由于后段管道截面收缩,测点压力值缓慢上升,当压力波到达三分支节点后产生反射波叠加,测点2压力值下降,最后逐渐稳定在0.147 MPa。测点2压力预测值与试验结果吻合度较高拟合度较好,平均值误差分别为4.6%、4.5%和4.2%,压力平稳段平均值误差分别为1.2%、1.0%和1.1%。等压模型假设交汇区域处各分支静压值相等,测点1与测点3压力值仿真结果在0.4 ms时迅速上升,并都稳定在0.076 MPa,仿真结果与试验测量结果趋势一致,但平稳段压力值有较大误差,平均值误差为29.8%。与等压模型不同,动量守恒模型和压损模型由于考虑各流径结构和流动参数引起的压力损失影响,测点1与测点3达到平稳段时压力值不同,与试验结果吻合度较好,两种模型测点1平稳段平均误差分别为10.20%和1.82%,测点3平稳段平均误差为7.17%和3.36%。压力损失系数模型由于基于实际测量压力损失数据建立,因此其计算精度较高。与等压模型相比,动量守恒模型预测精度已经有大幅提高,同时模型不依赖于试验数据,对于缺少压力损失试验数据的多分支接头计算具有一定的应用价值。

图7 不同多分支边界模型仿真与试验结果对比
从图7可以看出,仿真结果中压力波到达测点1和测点3的时间基本相同,而试验结果中压力波先到达测点1而后到达测点3,大约相差0.08 ms。这是由于仿真模型中忽略三分支管几何形状,假定其为节点,而在试验过程中,由于存在斜向分支,当压力波从斜向分支管道2向水平分支管道1和管道3传播时,压力波会先进入与其夹角小的管道1。由于间隔时间短,且其对压力波波形预测影响较小,所以在内燃机一维非定常流动仿真中通常可以忽略该微小的时间间隔。
2.2 仿真效率对比
在本算例中,等压模型虽然预测精度低,但是其计算效率高于其他两种模型。算例中模拟时间为1 ms,压力损失系数模型计算用时为1.12 s,动量守恒模型计算用时为1.56 s,而等压模型用时为0.36 s。这是由于压力损失系数模型和动量守恒边界模型有3个循环迭代过程,而等压模型仅有1个循环迭代过程,压力损失系数模型和动量守恒边界模型计算程序设计较复杂,迭代收敛较慢,模型计算效率较低。
2.3 3种模型适用性分析
表2从四方面对3种模型进行适用性分析,分析可知:从上述仿真结果对比中,可以很容易地看出各模型在计算时间和计算精度上的优势和劣势。动量守恒模型在建立过程中考虑了工质压缩性的影响,因此适用于可压缩流。等压模型对于多分支结构和流动状态没有限制,其通用性最好;动量守恒模型适用于有1个端口流入或1个端口流出的流动形式,模型的通用性略受影响;压力损失系数模型仅适用于有3个端口的结构形式,模型通用性最差。
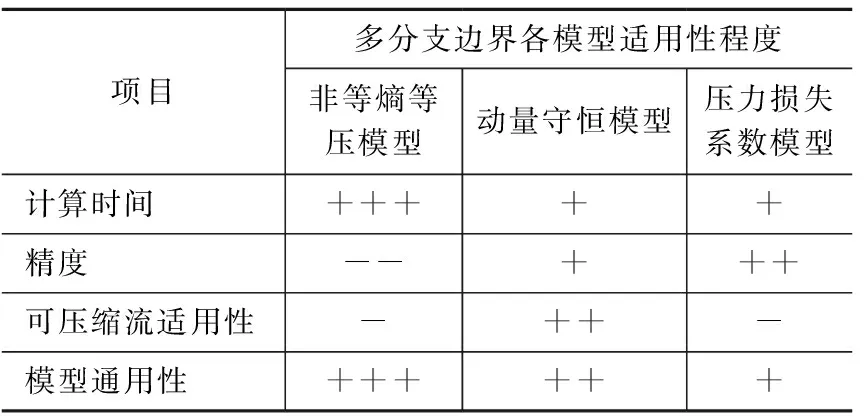
表2 三种模型适用性分析
因此,在考虑模型压缩性和通用性的基础上,通过平衡计算精度和计算效率,本文中建立的动量守恒模型可获得较好的综合优势。
3 模型整机验证
为验证本文中建立的多分支动量守恒模型对内燃机整机性能预测及排气压力波预测的准确性,针对文献[19]中某两级增压高功率密度内燃机标定转速工况建立整机循环仿真模型,管道计算采用TVD格式,缸内计算采用双Wiebe燃烧模型。考虑选用机型的进气马赫数较低(最高为0.25),可以忽略气体压缩性影响,同时为了减少计算耗时,进气歧管多分支接头均采用等压模型,排气歧管多分支接头分别采用等压模型和动量守恒模型,整机性能参数预测结果如表3所示。从表3中可以看出,采用等压模型时整机性能预测最大误差是空气流量的误差,为 217.47 g/(kW·h),转换为相对误差后为7.58%,采用动量守恒模型后该项误差为-65.7 g/(kW·h),转换为相对误差后为2.47%,计算精度得到提高。这主要是由于该机型排气过程中马赫数峰值将达到0.65,动量守恒模型考虑了工质压缩性的影响,误差降低。
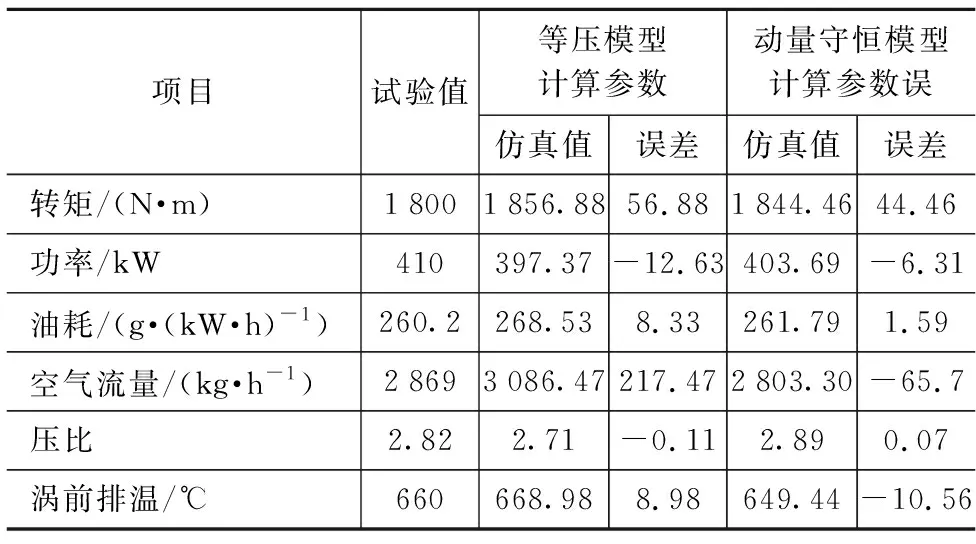
表3 多分支不同模型高功率密度内燃机性能预测结果
4 结论
(1) 在连续性方程和能量方程基础上,考虑到分支结构和流动参数影响造成工质流经多分支接头时的动量变化,建立了适用于任意分支数的多分支动量守恒边界模型。
(2) 相较于等压模型和压力损失系数模型,综合考虑模型的计算时间、计算精度、可压缩流适用性和通用性,本文中建立的内燃机歧管多分支动量守恒边界模型具有较大优势。
(3) 对于某型高功率密度内燃机,传统的等压模型在标定转速工况内燃机性能预测最大误差为7.58%,采用动量守恒模型后最大误差为2.47%,预测精度得到大幅提高。本文所提出的多分支动量守恒模型不依赖于试验数据,与传统的等压模型相比能够有效提高内燃机整机性能预测精度。
