基于地铁线路的常规公交局域网络协调调度模型

胡宝雨 艾雨豪 程国柱†

(1.东北林业大学 交通学院，黑龙江 哈尔滨 150040；2.北京交通大学 交通运输学院，北京100044)

随着我国城市居民对出行方式多样化的要求不断提高，居民借助多种交通方式完成一次出行的现象也更加常见。为保证不同交通方式间衔接顺利，提升居民出行效率，大部分城市正建设以常规公交为主体、地铁为骨干的多种交通方式相互协调的公共交通体系。其中，保证地铁与常规公交间有效的协调调度，是构建公共交通体系的基础。因此，设计合理的公交时刻表，对于优化基于地铁线路的常规公交局域网络的协调调度,则显得尤为重要。

关于公共交通网络协调调度与时刻表优化的关系，国内外学者进行了较为深入的研究，主要分为两大类：①以区域内车辆相遇总次数最大为目标建立优化模型。Kang等[1]指出了地铁发车时刻对乘客换乘时间的影响。Ceder等[2]分析了时刻表优化与车辆同步到达的关系，构建了单目标的同步换乘模型。石琴等[3]探讨了同步换乘的基础上多辆车在换乘点同时相遇的情况。刘志刚等[4- 5]均考虑同时优化乘客时间成本与企业运营成本，建立双目标优化模型。郭小乐等[6]则在以乘客时间成本与企业运营成本最小化为目标的优化模型中，加入了换乘等待时间过长下的乘客流失的惩罚机制。Wu等[7]构建了以乘客换乘时间、优化后的时刻表与原时刻表偏差最小化为目标的双目标优化模型。Guo等[8- 9]对轨道车辆间同步换乘进行研究，运用启发式算法对模型进行求解。马天山等[10]分析了一条地铁线路与一条接运公交线路在共同站点的同步换乘情况。Wei等[11]提出了公交与不同客运方式间同步换乘的时刻表优化模型。②考虑乘客换乘时间窗，以协同次数最大化为目标建立优化模型。吴影辉等[12- 13]考虑车辆协同到达时间窗，构建了车辆协同到达次数最大化的时刻表优化模型。Fouilhoux等[14- 15]探讨了车辆在高峰、平峰时期发车间隔变化的情况下，如何以协同次数最大化为目标建立时刻表优化模型。张姚等[16]根据站点重要性不同，对乘客等待时间设立相应权重，建立了乘客等待时间最小化的优化模型。

出行选择与换乘作为居民出行中的两种常见现象。例如，城市外围区居住的工作型客流需乘坐公交前往地铁站并换乘地铁到达城市中心区上班，在城市中心区的生活型客流需要乘坐公共交通工具前往超市、医院、游乐场等目的地，这部分出行者希望拥有多种出行选择前往目的地，在错过一种交通方式时能及时选用另一种交通方式出行。

本文将地铁线路与其相关联的常规公交线路组成的局域网络作为研究对象，把常规公交与地铁先后到达共同站点的时间间隔处于某一预先设定的时间范围(称为时间窗)记为1次协调(属于单向协调)；考虑公交线路与地铁间的关系，将局域网络分为协同换乘子网络与协作运输子网络；在线路发车间隔、时间窗约束下，构建了一种从子网络优化入手，达到局域网单向协调最大化的双目标优化模型，并运用启发式算法求得与地铁线路协调调度的常规公交时刻表，以便在提升换乘效率的同时，为居民提供多种出行选择机会，使出行者在错过地面公交时能及时转入地下乘坐地铁，完成一次“无等待”的出行。

1 问题描述

本文构建了一个基于地铁线路的常规公交局域网示意图，如图1所示。图中：b为地铁线路与公交线路的共同站点，k为共同站点总数；公交线路i的发车间隔di，由于受到运营成本、客流量等的影响，将会介于一个最小发车间隔hi和最大发车间隔Hi之间；fi、fj分别为规划周期内公交线路i、地铁线路j发出的总车次数。

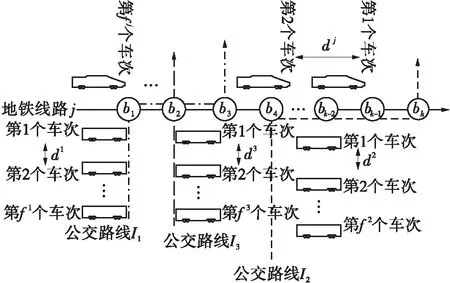
图1 基于地铁线路的常规公交局域网示意图

根据地铁线路与其关联公交线路的布局关系，可将常规公交局域网内线路分为协同换乘线路和协作运输线路。协同换乘线路、协作运输线路则分别构成协同换乘子网络与协作运输子网络。协同换乘、协作运输线路的分类根据公交线路的比例系数μ界定：

μ=ki/ci

(1)

式中，ki、ci分别为公交线路i上共同站点的数量和所有站点的数量。

当线路的比例系数满足0<μ<0.5时，该线路属于协同换乘线路；当线路的比例系数满足0.5≤μ≤1时，该线路属于协作运输线路。因此图1中，I1、I3为协同换乘线路，并构成协同换乘子网络；I2为协作运输线路，并构成协作运输子网络。

协同换乘线路与地铁线路相交于少数共同站点，这些共同站点则作为枢纽站点供乘客换乘地铁；协作运输线路与地铁线路有较长的共线路段，共线路段上众多共同站点为出行者提供更多的出行选择机会：地铁或是公交。因此，为使居民在枢纽站点换乘时有足够的时间从正在乘坐的公交车下车换乘地铁,在共线路段出行时能在错过地面公交的情况下及时进入地下乘坐地铁完成出行,应对协同换乘子网络与协作运输子网络分别设立不同的时间窗，令协同换乘子网络与协作运输子网络内协调次数最大化，同时保证乘客在枢纽站点集中换乘，在共线路段有更多的出行选择机会。为此，协同换乘线路的协调应在尽量少的共同站点集中发生，协作运输线路的协调应在尽量多的共同站点分散发生。为解决此问题，需构建双目标优化模型，以降低乘客的出行等待时间，提高出行效率。

2 模型的构建

由于高峰时期公交、地铁发车间隔均较小，只要公交能按照时刻表运行，公交与地铁就能够达到相互协调运行的状态。为此，本文以平峰时期为研究场景，构建基于地铁线路的常规公交局域网络协调调度模型，模型假设如下：

(1)不考虑二次候车，在共同站点处乘客将会乘坐第一趟到达的车次，不会因为其他因素而考虑继续等待下一个车次；

(2)公交车与地铁均严格按照时刻表运行，不会出现中途停车与掉头现象。

(2)

(3)

由式(1)可将局域网络分为协同换乘子网络与协作运输子网络，当两个子网络的协调次数Y1、Y2同时达到最大化时，

(4)

(5)

建立优化目标函数1，使局域网络内总协调次数Y达到最大化，即

(6)

式中，IM和IN分别为协同换乘线路集合和协作运输线路集合，M、N分别为协同换乘、协作运输线路上共同站点的集合，Bij为公交线路i与地铁线路j的共同站点集合。

(7)

建立优化目标函数2，使协同换乘子网络上的协调点数Z1最小化、协作运输子网络上的协调点数Z2最大化(若干辆公交与地铁在同一个共同站点内产生协调，则记为1个协调点数)，即

(8)

(9)

约束条件为

(10)

(11)

(12)

(13)

(14)

(15)

3 模型求解

本文所建立的模型为复杂的整数双目标优化问题，启发式算法更适合该类问题的求解，能够在合理时间内获得满意解。为方便叙述，下面对一些概念进行定义。初始共同站点：至少有一条确定发车间隔的公交线路经过该共同站点，该线路发车次数小于fi。有效共同站点：线路i在初始共同站点确定了发车间隔，称该共同站点为线路i的有效共同站点。有效初始发车时刻范围：线路在有效共同站点确定的初始发车时刻范围。本文启发式算法以基于地铁线路的常规公交局域网内共同站点的选择为基础来确定公交线路各班次的发车时刻，算法的流程图如图2所示，具体的步骤如下。

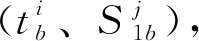
2)所有共同站点初始化为初始共同站点。

3)根据式(1)对公交线路进行分类，若线路为协同换乘线路，则转步骤4)，否则转步骤5)。

4)按照协同换乘模块计算。

图2 模型求解流程

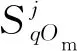
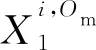
(16)

(17)

发车间隔di按照以下方法确定，即

hi≤di≤Hi

(18)

(19)

(4.3)确定发车间隔已知的公交线路的初始发车时刻。为使线路上的协调次数最大化，公交车辆应尽可能在除有效共同站点外的其他共同站点与地铁产生协调。根据式(20)求出公交线路在除有效共同站点外的其他共同站点与地铁发生协调的初始发车时刻范围，

(20)

判断有效初始发车时刻范围是否与上述求出的初始发车时刻范围产生交集，最终求出的交集需保证公交车能在有效共同站点和尽量多的其他共同站点与地铁发生协调。公交线路初始发车时刻为交集内的下限值。

(4.4)判断协同换乘线路上是否还存在初始共同站点，如果存在则证明有公交线路发车频率小于原始发车频率，算法需转到步骤(4.1)直至遍历完所有初始共同站点，使协同换乘子网络中不存在初始共同站点，保证优化后的发车频率与原发车频率一致，协同换乘模块子流程结束。

5)按照协作运输模块计算。

(21)

(22)

协作运输线路发车间隔di按照式(18)、(19)确定。

(5.3)与步骤(4.3)相同。

(5.4)判断协作运输线路上是否还存在初始共同站点，如果存在则证明有公交线路发车频率小于原始发车频率，算法需转到步骤(5.1)直至遍历完所有初始共同站点，使协作运输子网络中不存在初始共同站点，保证优化后的发车频率与原发车频率一致，协作运输模块子流程结束。

4 算例分析

图3为某地区地铁与公交线网图，包含1条地铁线路j、5条常规公交线路(I1,I2,…,I5)，而b1,b2,…,b14为共同站点。建立共同站点数据结构，包括公交线路从始发站到各共同站点的行程时间(见表1)与地铁线路首班车到达各共同站点的时刻(分别为0:09、0:14、0:19、0:24、0:29、0:33、0:37、0:41、0:45、0:48、0:51、0:54、0:57、0:60)。

图3 实际的地铁与公交线网图

初始化，使所有共同站点均为初始共同站点，并根据式(1)对公交线路进行分类，建立地铁线路以及各条公交线路的数据结构，包括hi、Hi、fi、fj和经过共同站点编号Bij，如表2所示。

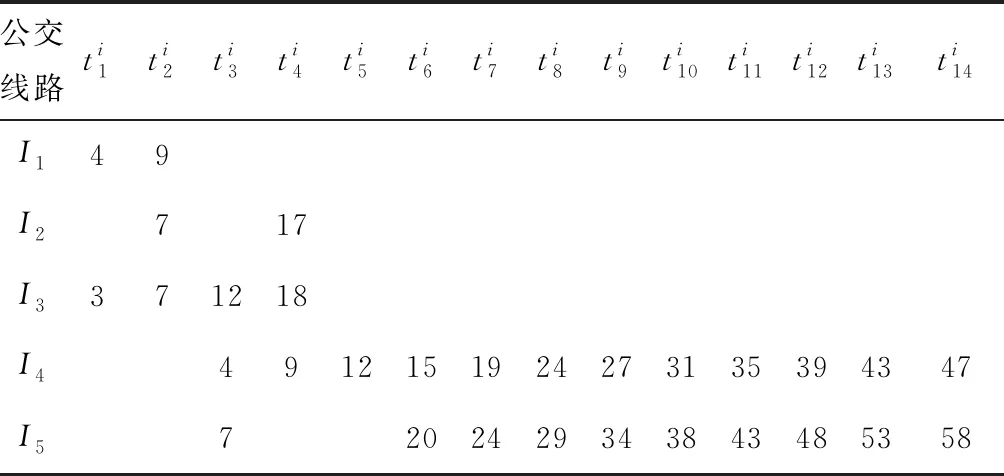
表1 公交线路从始发站到各共同站点的行程时间

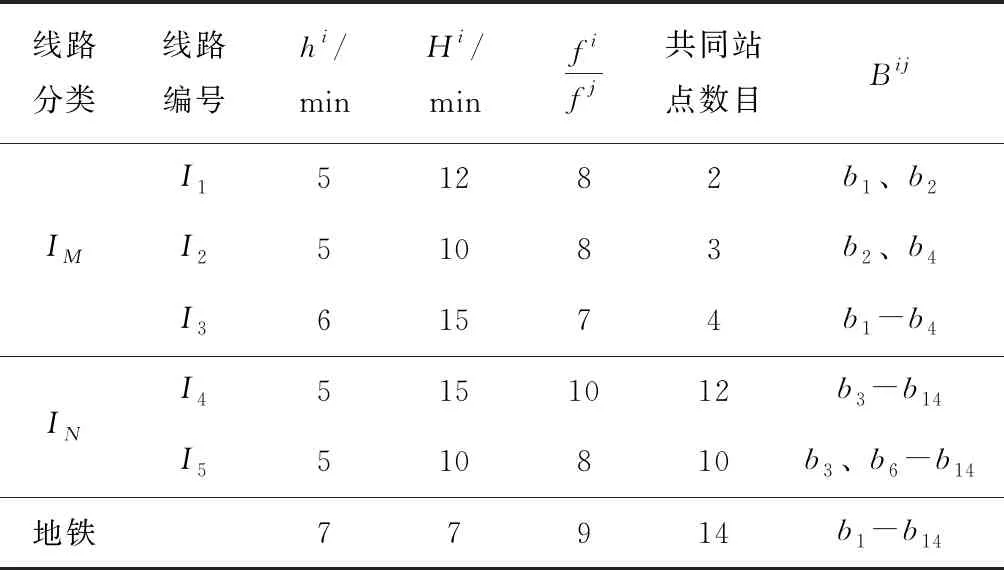
表2 线路数据结构

根据表2，本算例中协同换乘线路为I1、I2、I3，协作运输线路为I4、I5。I1、I2、I3根据协同换乘模块计算，协同换乘线路上的共同站点的时间窗取[2,4]。I4、I5根据协作运输模块计算，协作运输线路上的共同站点的时间窗取[1,3]。

4.1 协同换乘模块计算

执行步骤4)协同换乘模块。

(4.1)从初始化有效共同站点中选择Om点。对于条件①，算例中公交线路发车时刻均未确定，故无法确定Om点；对于条件②，通过共同站点b2的协同换乘线路最多；对于条件③，只有b2满足条件②。故选择b2作为Om点。

(4.3)确定各线路的准确发车时刻。将在共同站点b2求出的初始发车时刻范围作为有效初始发车时刻范围，其余共同站点所推出的初始发车时刻范围见表3。

表3 线路I1、I2、I3的初始发车时刻范围

选择交集范围内发车时刻的下限值，得到协同换乘线路时刻表(见表4)。

表4 协同换乘线路的时刻表

协同换乘线路时刻表确定后，协同换乘模块内不存在初始共同站点，故协同换乘模块子流程结束。

4.2 协作运输模块计算

执行步骤5)协作运输模块。

(5.3)确定线路I4的初始发车时刻后，可推出其余共同站点b5,b6,…,b14的初始发车时刻范围为[0:14,0:15]、0:15、[0:11,0:13]、[0:14,0:15]、0:15、[0:14,0:15]、[0:13,0:15]、[0:12,0:14]、[0:11,0:13]、[0:10,0:12]。

选择交集范围内发车时刻的下限值，得到线路I4的初始发车时刻为0:14。

(5.4)由于还存在初始共同站点，故返回步骤(5.1)，选择共同站点b3作为On点，同理求得线路I5的初始发车时刻为0:10，发车间隔d5=7，发车次数f5=8。协作运输线路的时刻表见表5。

协作运输线路时刻表确定后，协作运输模块内不存在初始共同站点，故协作运输模块子流程结束。

4.3 结果分析

根据表4、表5公交线路时刻表计算，本模型求解结果见表6。该公交局域网内总协调次数Y=94；协同换乘线路协调次数达到55，协调点数却只有27；协作运输线路中协调次数达到39，协调点数为30。

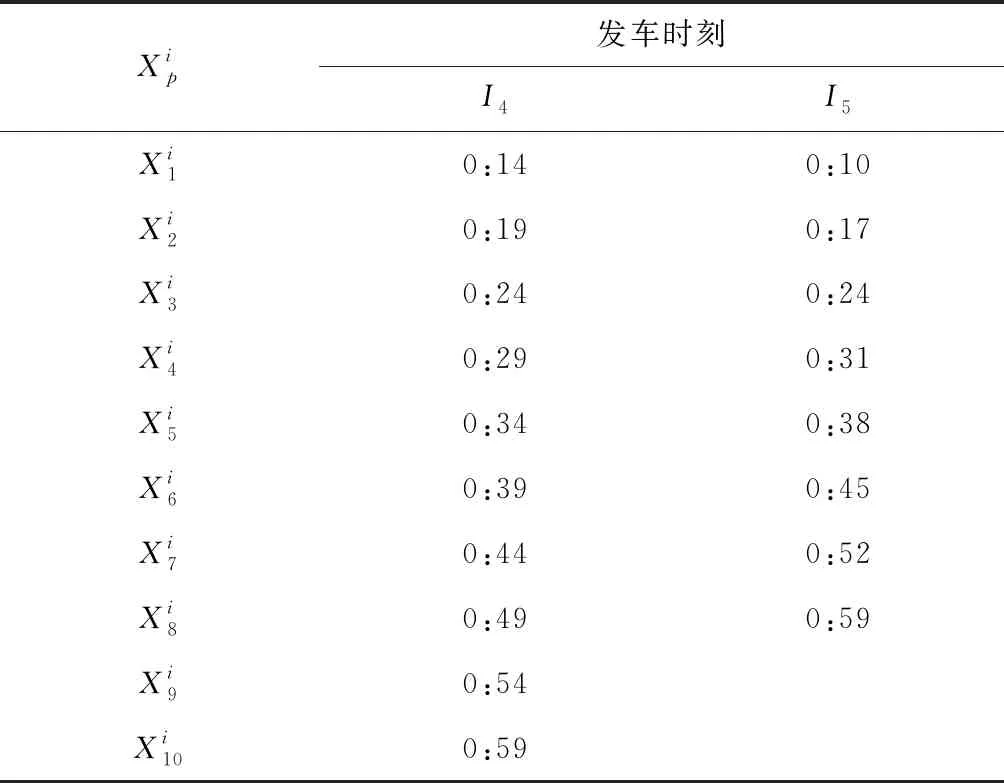
表5 协作运输线路的时刻表

表6 模型求解结果

上述分析结果表明：该模型和启发式算法能在保持公交线路发车频率不变的情况下，最终输出与原发车频率一致的常规公交时刻表，在提高与地铁线路运营的协调性的同时，避免了导致公交线路发车频率过高和供需不平衡的现象。该时刻表以局域网内与地铁协调总次数最大化为第一目标，保证协同换乘子网络内多辆公交车与地铁产生协调的几率最大、协作运输子网络内多辆公交车与地铁产生协调的几率最小为第二目标，说明协调优化后的时刻表能够为出行者提供更多的出行选择，减少乘客在出行过程中的等待时间。

5 结论

本文针对地铁线路与常规公交线路间的协调调度问题，从分析二者布局关系入手，在整个局域网络背景下，将网络划分为协同换乘子网络与协作运输子网络，并对不同类型线路设立不同的时间窗；在发车间隔、时间窗的约束下，构建基于地铁线路的常规公交局域网络协调调度模型，通过对公交初始发车时刻以及发车间隔的调整来实现整个网络内总协调次数最大化的目标，并保证协同换乘子网络内协调点数最小化、协作运输子网络内协调点数最大化；针对双目标整数混合优化问题的复杂性，设计了启发式算法，并借助算例分析了算法的有效性，该算法能对两个目标同时进行优化，从而达到局域网络内部地铁与公交协调调度的最佳状态。

本文的应用场景为平峰时期的交通系统，此时道路运行条件较好，车辆运行顺畅，到站准时性较高；结合公交专用道、信号优先等智能公交手段，能最大限度降低地面交通对公交到站时刻的影响，提升公交准时性。目前公交到站时刻具有一定的不确定性，可将模型拓展，在车辆到站时刻、发车间隔内加入不同的浮动因子，以模拟公交到站时刻与发车间隔的浮动变化。