乘员胸部钝性冲击下主动脉瓣的动力学响应

童芳 兰凤崇 陈吉清 李雄

(华南理工大学 机械与汽车工程学院，广东 广州 510640)

在人体正常生理状态下，心脏的周期性收缩可保证体内的血液循环。主动脉瓣是血液循环中连接左心室和主动脉的重要阀门，保证血液的单向流动。当汽车乘员胸部受到钝性冲击时，心脏及主动脉内血压突变直接冲击主动脉瓣，导致主动脉瓣膜功能受损而可能引发充血性心力衰竭或死亡[1- 2]。因此，在胸部钝性冲击下针对瓣膜及其周围血液的动力学分析，对其损伤机理研究以及汽车乘员保护具有重要的意义。在心动周期的任意动态时刻，心肌及血管的形态、血液流速及压力等都在不断变化。活体动物试验以及人体尸检研究表明：心脏在不同心动周期受到撞击时的损伤存在差异[3- 5]；胸部主动脉压力在不同时刻胸部碰撞下的最大值和波形变化都很大[6]；胸部钝性冲击引起的瓣膜破裂以及脱落更容易发生在舒张期，此时瓣膜关闭并且跨瓣压差增大[7- 9]。这些研究都强调了与心动周期有关的胸部碰撞时刻对瓣膜及心血管系统的钝性冲击损伤有不可忽视的影响。

对人体生理状态下钝性冲击的响应分析的主要难点是人体生命特征和人体精细化结构。目前，在实验方面，用于台车碰撞实验的尸体标本(PMHS)没有生命特征，所以关于撞击时刻对损伤影响的研究大多停留在活体动物实验的水平[6,10- 12]。由于实验条件的限制，准确地获取瓣膜血液的物理特性，并量化不同碰撞时刻下的损伤差异是困难的。不仅如此，活体动物实验虽然在心动周期等方面解决了生命特征的问题，但动物跟人体在结构上的固有差异，必然影响碰撞的损伤形式。尤其当涉及瓣膜血液等流体和固体的相互作用时，结构的差异会放大整体响应结果的差异。在数值模拟方面，基于人体结构的生物力学仿真是一种研究损伤响应和机理的重要方法。目前的损伤生物力学模型，如丰田的安全人体模型(THUMS)[13]、全球人体联盟模型(GHBMC)[14]、福特的整人模型[15]、中国人体模型(CHUBM)[16]，在人体碰撞损伤研究方面都取得了重要的进展。文献[17]建立了精细的人体上肢有限元模型并研究了乘员侧碰下的锁骨骨折问题。文献[18- 19]利用肋骨变形、胸部黏性准则或胸部接触力等数据来评估胸部整体的响应。文献[20- 21]通过部分器官如肺、肝、整体的应力应变来研究其损伤风险。然而，这些模型主要研究人的整体响应，在精细化建模方面关注不足。没有人体的详细解剖结构，如主动脉瓣、主动脉根部，也缺乏血液的表达，无法分析胸部钝性冲击下心脏瓣膜以及血液的动力学响应。

研究生理状态下瓣膜的钝性损伤响应，不仅存在精细化建模、生理边界模拟等问题，当模拟生命特征时，血液与瓣膜的耦合计算方法也是难点。由于主动脉瓣的非线性大变形以及导致的流体域畸变等问题，将结构响应和血流动力学结合起来进行计算分析，一直是一个挑战。目前常用的流固耦合(FSI)模型大部分都是通过基于网格的方法建立的[22- 26]，例如任意拉格朗日欧拉法(ALE)需要在计算过程中保持高的网格质量。浸入边界法(IBM)是一种用于求解结构浸没在流体网格中的问题的无边界协调方法。这些方法在流固耦合方面各有特点，然而仍然有一些局限性，如数值不稳定、网格重构耗时、流体域碎片化以及计算成本高等。近些年，光滑粒子动力学(SPH)方法逐渐被用于解决复杂的流固耦合问题，它是一种基于拉格朗日粒子的无网格方法，可用于解决几何和边界的大变形以及流体域的碎片化等问题，用其解决主动脉瓣与血液间的耦合问题具有重要的意义。

为了解决流体域畸变引起的计算不稳定性问题以及流体域分割等难点，本文采用SPH方法建立了一个主动脉瓣与血液的FSI模型，用于分析胸部钝性冲击产生的突变血流与压力下主动脉瓣的动力学响应，其中主动脉瓣采用有限元(FE)方法进行建模，主动脉瓣内的血液利用SPH粒子将其离散化;然后分析了主动脉瓣在正常生理边界条件下一个心动周期的响应并与实验对比，以验证模型的可靠性；最后，将动物实验在不同心动周期(射血期、舒张早期、舒张中期)碰撞时所产生的突变血压边界条件与人体生理条件相结合，施加到模型上，分析碰撞时刻对瓣膜动力学响应的影响，并对瓣膜径向位置变化、瓣膜的应变及应力变化等仿真结果进行了评估。

1 主动脉瓣-血流的FE-SPH耦合模型

在生理条件下，心脏收缩期时血液由左心室经过主动脉瓣流向主动脉，舒张期时左心室停止向主动脉射血，其中主动脉瓣的开闭运动保证了血液的单向流动，如图1(a)所示。瓣膜组织柔软，在血液中运动时会引起流体域边界的大变形。当使用基于网格的方法来模拟流体域时，为了避免网格畸变，需要在计算过程中不断重新划分流体域网格，以保证高的网格质量，这将耗费大量的时间与计算资源。当瓣膜完全关闭时，还会将流体域切割成不相连的子区域(见图1(b))，这种问题对于基于网格的FSI方法来说仍是一个难点。尤其在钝性胸部碰撞载荷下会引起主动脉瓣内的血压急剧变化以及瓣膜的不规律运动，以上流体域网格畸变问题将会加剧，给计算带来更大的挑战。

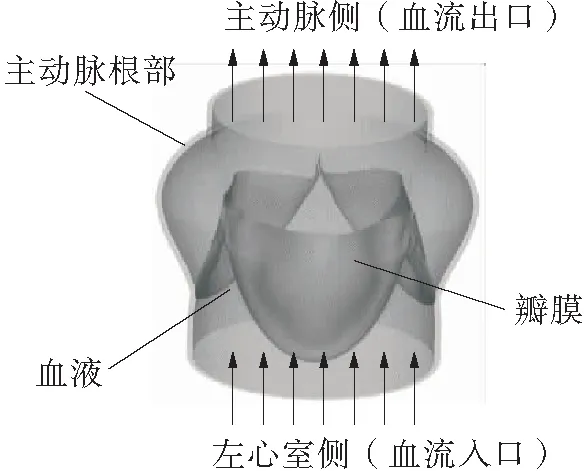
(a)主动脉瓣结构与生理功能

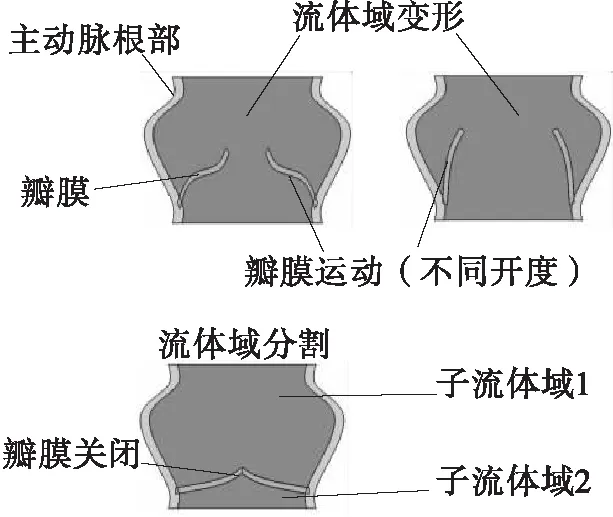
(b)血液流体域变形2D示意图

SPH方法是利用拉格朗日形式的纳维-斯托克斯方程来求解,而不是传统的欧拉形式。利用SPH方法建立瓣膜和血液的耦合模型，将流体域离散成一系列的球形粒子。与每一个粒子相关联的流体体积为其外切小正方体的体积，其中正方体边长的一半称为粒子的特征长度。所有粒子加在一起时，这些立方体将填充整个流体体积(见图2)。

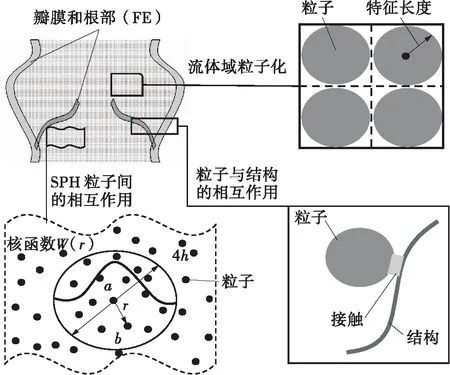
图2 主动脉瓣-血液的FE-SPH耦合模型

每一个SPH粒子都有压力、流速等物理特性来表示周围的液体。粒子间不需要通过网格来连接，任意粒子的物理性质都是周围粒子通过核函数W(r)插值得到的，其数学表达方法为[27]

(1)

式中：A、r、m和ρ分别为粒子的物理性质、位置、质量和密度；下标a和b分别表示不同位置的粒子a和粒子b；W(·)为核函数；h为光滑长度，它决定着每一个点有多少个粒子参与插值。

SPH框架下的质量、动量守恒可表示为

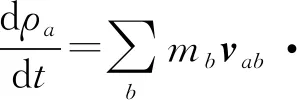
(2)

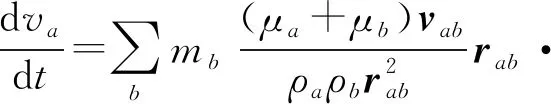
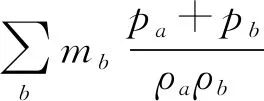
(3)

式中，vab为粒子a和b的相对速度，rab是粒子a和b的相对位置，Wab为粒子a和b之间的核函数关系，pa、pb分别为粒子a、b的压力。

主动脉根部和瓣膜采用FE方法进行建模。模拟血液的SPH粒子可以通过接触与主动脉根部及瓣膜进行相互作用。此时流体粒子被看作是一个基于节点的面，与有限元网格通过基于罚函数接触算法传递数据。

1.1 主动脉根部和瓣膜的结构化

医学上在建立人工瓣膜时，利用5个尺寸设计参数(基准半径Rb、缝合半径Rc、主动脉高度H、缝合高度Hs及瓣膜开启时与垂直方向的夹角β)来描述瓣膜的几何形状[28]。多项式函数拟合的主动脉根部能够较好地模拟出其几何形态特征[29]。本研究基于此建立了主动脉根部和瓣膜的几何模型，如图3所示，详细尺寸来源于志愿者CT扫描，具体如下：瓣膜参数Rb=12.41 mm，Rc=11.04 mm，H=14.27 mm，Hs=2.60 mm，β=5.5°；主动脉根部参数中，中心点到主动脉窦的最大径向距离L1=17.00 mm，中心点到主动脉心室连接处的距离L2=11.04 mm，主动脉窦的特征角α=60°。

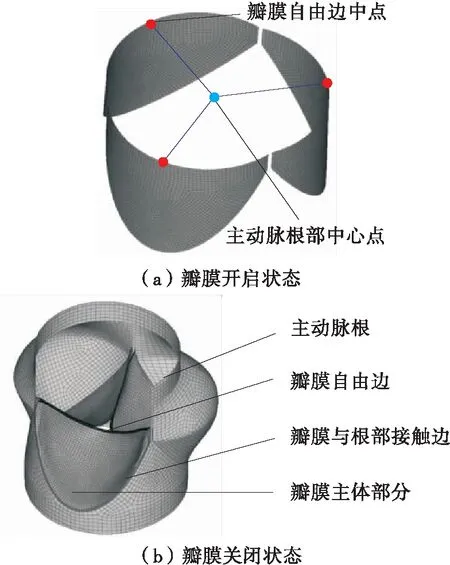
图3 主动脉根部及瓣膜的FE模型

将建立的几何模型导入Hypermesh中进行网格划分。瓣膜包含5 838个四节点壳单元，厚度为0.3 mm，主动脉根部包含5 736个四节点壳单元，厚度为0.6 mm。由于生理状态下瓣膜的变形远大于主动脉根部，故在模型中将主动脉根部假设为刚体，与瓣膜之间用绑定约束。主动脉瓣作为一种生物软组织材料，具有变形非线性及不可压缩的特性,本文采用Ogden超弹性模型来表示它的性质，其应变能函数表示如下：

(4)

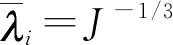
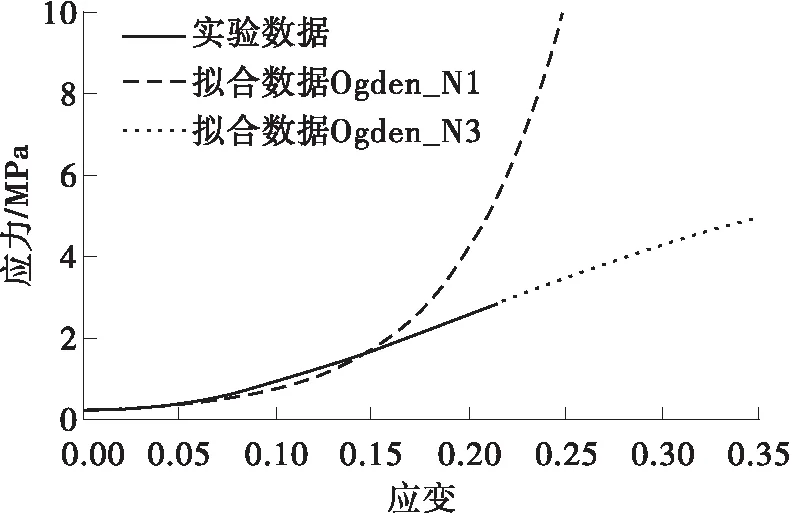
图4 瓣膜材料模型的拟合结果

用以上方法建立的瓣膜是处于开启状态(如图3(a)所示)，然而瓣膜的无应力状态通常认为是关闭的。为了达到关闭的形态，施加一个11.33 kPa的均匀压力到主动脉侧、0.93 kPa的压力到左心室侧[31]。变形后的网格如图3(b)所示，将其保存为瓣膜的初始形态进行后面的仿真。

1.2 血液的粒子化

血液SPH粒子的流体力学行为是通过状态方程来描述的，将压力定义为密度和内能的函数。本研究中采用的Mie-Grüneisen状态方程适用于模拟高压下的流体，其常见形式为

(5)

式中，Γ0、c0和s为材料常数，ρ为当前密度，ρ0为参考密度，Em为单位质量的内能，η为公称体积压缩应变。其中血液被看作是牛顿流体[32]，在人体正常体温(37 ℃)下，设置其密度为1 056 kg/m3，动力黏度为0.003 5 Pa·s。为了使模拟的血液具有良好的流动性与扩展性，将流体域划分成30 996个SPH粒子。参考网格大小敏感度验证[33]，将粒子的特征长度设置为0.7 mm。仿真的增量步长控制在10-7到10-6范围内，以保证计算稳定性的同时减少计算资源的消耗。

2 生理及碰撞条件下的仿真

2.1 仿真模型

在主动脉根部FE模型的上游和下游连接两根刚性管道并固定在空间中。粒子化的血液在主动脉瓣两侧足够远的距离均匀地充满整个主动脉根部以及刚性管。通过在固定体积的血液两侧施加压力载荷，使主动脉瓣周围的血液产生速度和压力，推动瓣膜的开启和关闭运动。SPH粒子的特性使其边界条件的施加不像有限元那样直接。压力等分布载荷不能直接施加在粒子上，而是通过施加在刚性板上并设置与粒子间的接触作用间接施加在主动脉两侧的血液上[33]。仿真模型如图5所示，通过在两侧刚性板上施加不同的压力载荷来模拟生理状态及碰撞载荷下的主动脉瓣响应。

2.2 正常生理条件下模型的验证

根据FSI关系与仿真模型的加载方式，有必要首先考虑并论证正常生理条件下瓣膜和血液的作用关系。图6(a)显示了正常生理条件下一个心动周期内主动脉与左心室的血压变化[34]。当t=0 ms时，左心室与主动脉内血压相等，主动脉瓣的跨瓣压差为0，瓣膜处于无应力状态。随后在心脏的收缩下左心室压力大于主动脉，主动脉瓣开启，左心室向主动脉内射血。当左心室射血完毕时主动脉瓣开始关闭，在300 ms左右主动脉瓣完全关闭，直至下一次心脏收缩。将此非线性压力边界施加到仿真模型，仿真持续整个心动周期，时间为800 ms。主动脉瓣在正常心动周期内的运动用瓣膜自由边中点的径向位置来表示，它能够表征瓣膜的有效开口面积。将本文FSI模型与文献[24，35- 36]方法(见表1)的仿真结果进行对比，如图6(b)所示。从图中可知：本文模型仿真得到的主动脉瓣的开启与关闭时刻、径向开口的最大值均在文献范围内；瓣膜径向位置的变化速率与文献结果具有一致性，证明了本文建立的FSI模型的有效性。

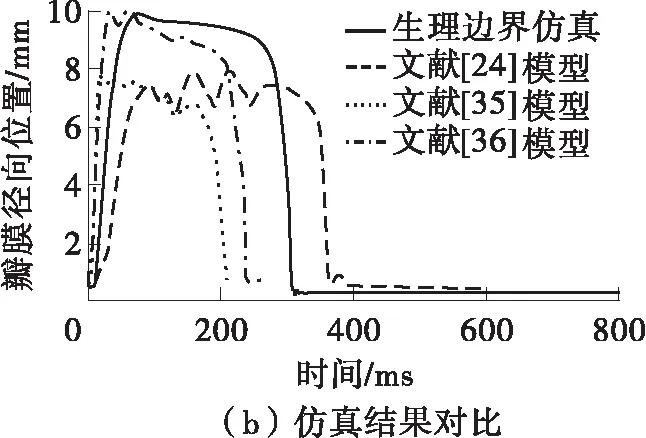
图6 生理条件下FSI模型的仿真结果比较

Fig.6 Comparison of simulation results of FSI models under physiological condition

2.3 动态血流压力边界条件

定义胸部钝性冲击引起的高压血流边界条件是具有挑战性的。在碰撞台车实验中，尸体与活人相比，死后心跳停止以及材料性质的改变都可能会对碰撞响应产生影响[10]。基于活体动物的碰撞实验能够解决“活”的问题，而猪与人在瓣膜结构和材料方面都具有极高的相似性[2]，故本研究采用了麻醉猪的碰撞实验结果来获取胸部碰撞产生的压力边界条件。Kroell等[6,11]利用41头猪进行了不同碰撞速度、压缩量以及碰撞时刻的实验，其中有3例实验(见表2)利用相同型号的传感器记录了左心室和主动脉的压力在碰撞过程中的变化。在3种突变血流仿真(见图7)中，碰撞时刻前施加在两侧刚性板上的压力为人体生理压力，碰撞时刻开始施加的是来源于动物实验的高压边界条件。仿真从喷射初期开始，碰撞后20 ms结束，记录瓣膜的应力、应变以及指定点的位移。

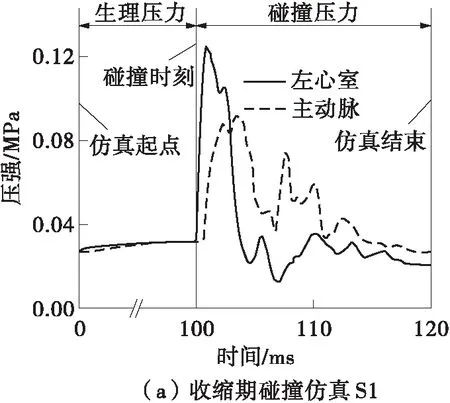
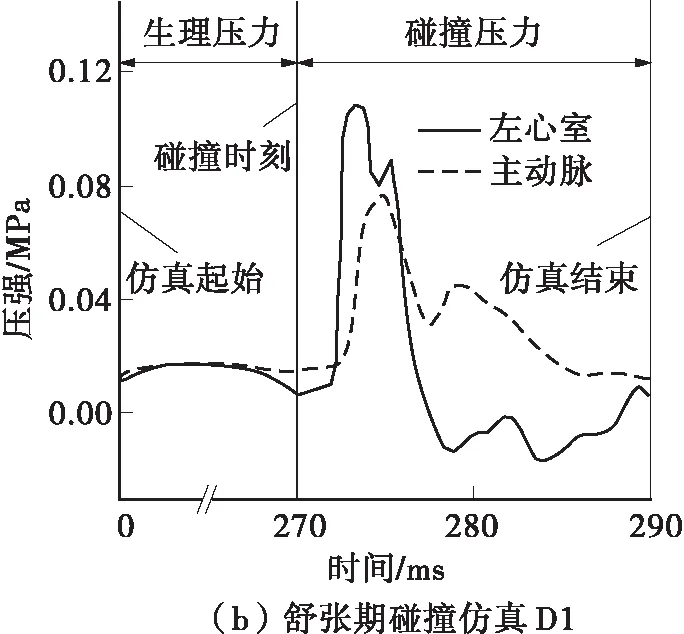
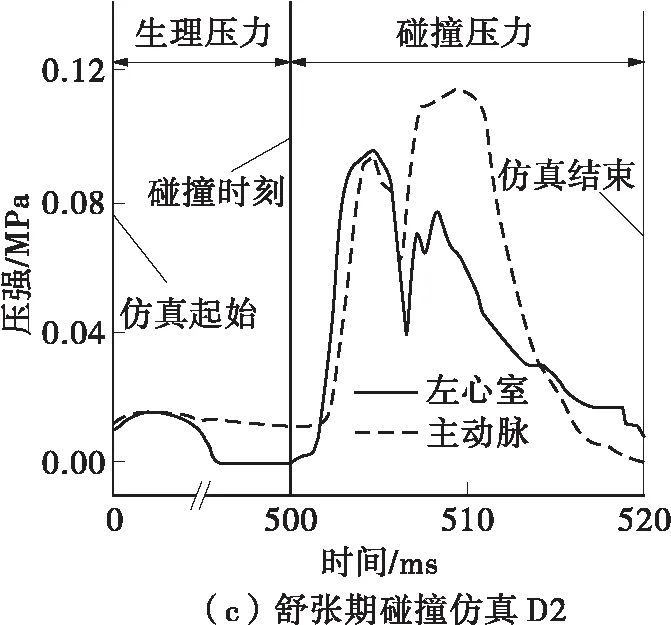
图7 仿真的压力边界条件

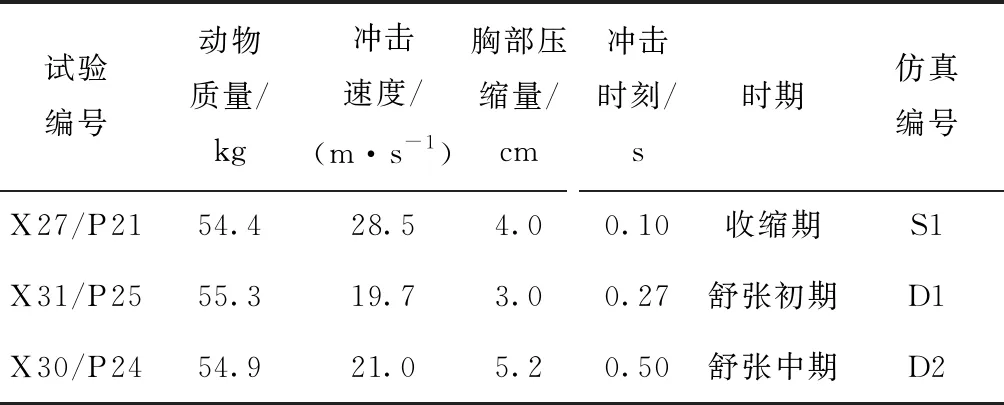
表2 实验中动物尺寸和碰撞参数

3 主动脉瓣的动力学响应分析

3.1 主动脉瓣的运动学响应

主动脉瓣的运动是通过瓣膜自由边的中点(见图3(a))的径向位置-时间关系来评估的，它能够表征瓣膜运动过程中的有效开口面积。由于仿真过程中3个瓣膜的运动学很相似，故采用它们的平均径向位置的改变来分析。与正常生理条件下相比，在3种碰撞血流边界条件下瓣膜的运动都受到了干扰，如图8所示。在仿真S1和D1中，瓣膜径向位移先是大于正常值，然后迅速减小到低于常压。可能是由于碰撞初期大量的血液由左心室流入主动脉，使瓣膜的有效开口面积增大。随后由于左心室内的压力比正常情况下下降得更快，导致瓣膜在主动脉的压力下加速了关闭过程。在仿真D2中，最初瓣膜的径向位置几乎不变，因为此时主动脉内血压远高于左心室，瓣膜的单向阀作用使其处于关闭状态，阻止血液通过；在碰撞发生15 ms之后瓣膜才逐渐打开，平衡瓣膜两侧压力差。

3.2 主动脉瓣的应变响应

瓣膜在3种钝性冲击引起的血流边界条件下的应变云如图9所示。在仿真S1中，应变在103.5 ms时达到最大值(约为0.23)，集中在瓣膜与主动脉根部的接触边。这是由于碰撞使左心室受到挤压加速射血，大量血液在短时间内通过主动脉瓣使其接触边产生拉伸力。在仿真D1中，大的应变先是集中在瓣膜底部靠近接触线处，然后随着瓣膜的关闭过程逐渐扩展到腹部。瓣膜的最大应变比仿真S1中的小，约为0.18。在仿真D2中，由碰撞引起的主动脉压力远大于左心室压力，使瓣膜处于紧紧关闭的状态，最大应变达到0.35；在碰撞15 ms之后，主动脉瓣两侧的压差逐渐恢复到正常水平，瓣膜的应变也随之减小。在准静态拉伸实验中，瓣膜的失效应变约为0.3±0.12[37]。由上面结果可以看出，仿真S1和D1中瓣膜损伤的可能性较小，而在仿真D2中的最大应变接近于静态拉伸的失效应变，有更高的损伤风险。

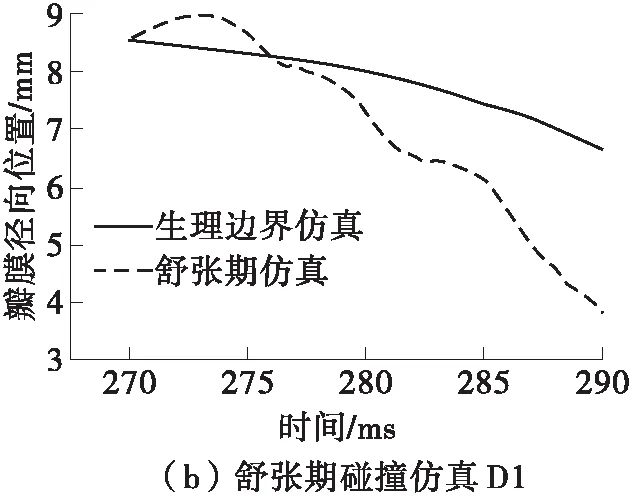
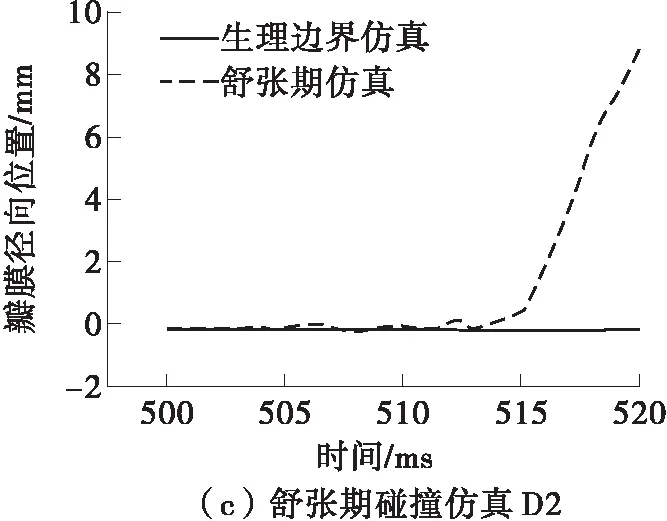
图8 瓣膜自由边中点的径向位置随时间的变化

3.3 主动脉瓣的应力响应

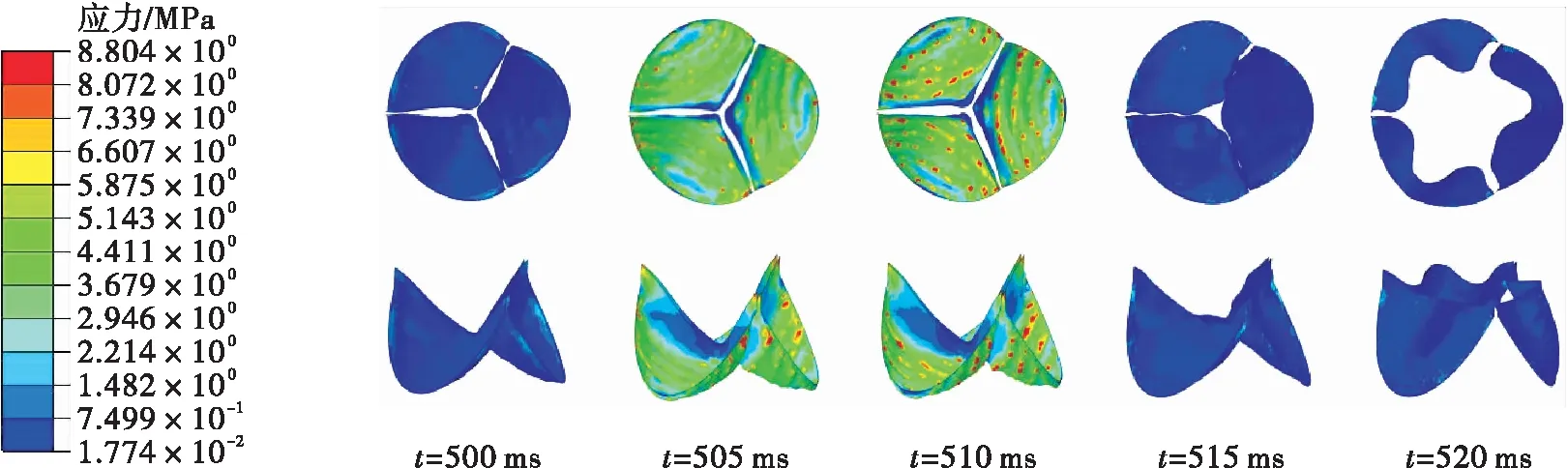
瓣膜在3种钝性冲击引起的血流边界条件下的应力云图如图10所示。在仿真S1中，应力在102.5 ms时达到最大值(约为1.078 MPa)。在仿真D1中，瓣膜的最大应力比仿真S1中的小，约为0.716 MPa，集中在瓣膜与根部的接触区域。在仿真D2中，最大应力在瞬时达到了8.8 MPa，发生在506.5 ms时；大的应力主要分布在瓣膜的腹部，该位置是血压载荷的主要承受区域。从应力大小来看，仿真D2的瓣膜拥有更高的损伤风险。在仿真D2中，由于主动脉内产生了突变的血液压力波，使主动脉瓣在高压血流的冲击下关闭，在瓣膜的缝隙之间部分的血液返流回左心室，在主动脉瓣上形成褶皱，使得瓣膜容易形成撕裂伤。这与Mehta等[7]的研究结果一致：主动脉瓣的损伤往往伴随着主动脉内的突升血压与主动脉瓣的反流现象。

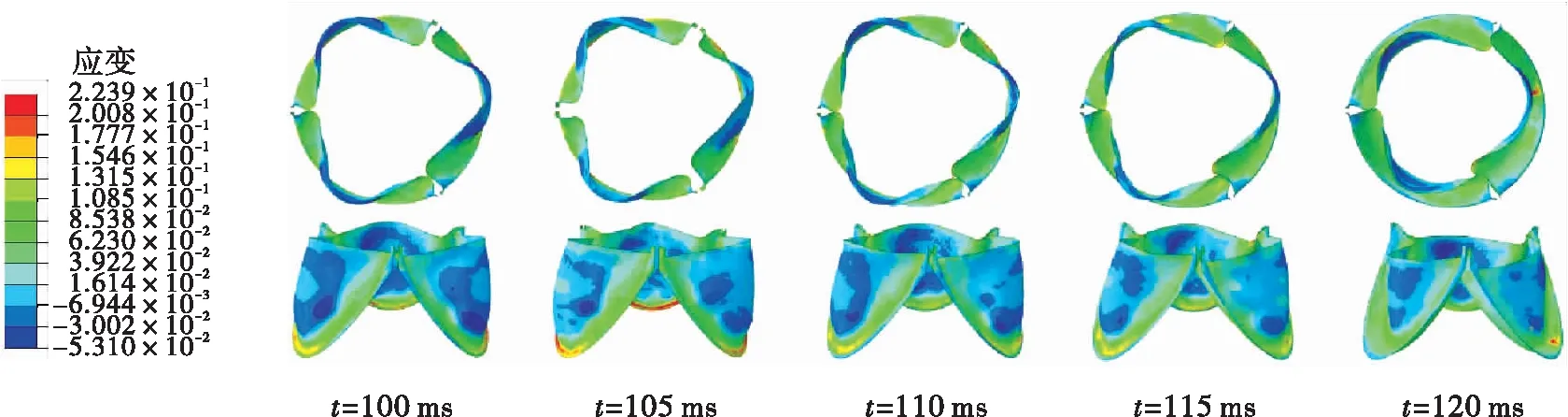
(a)仿真S1

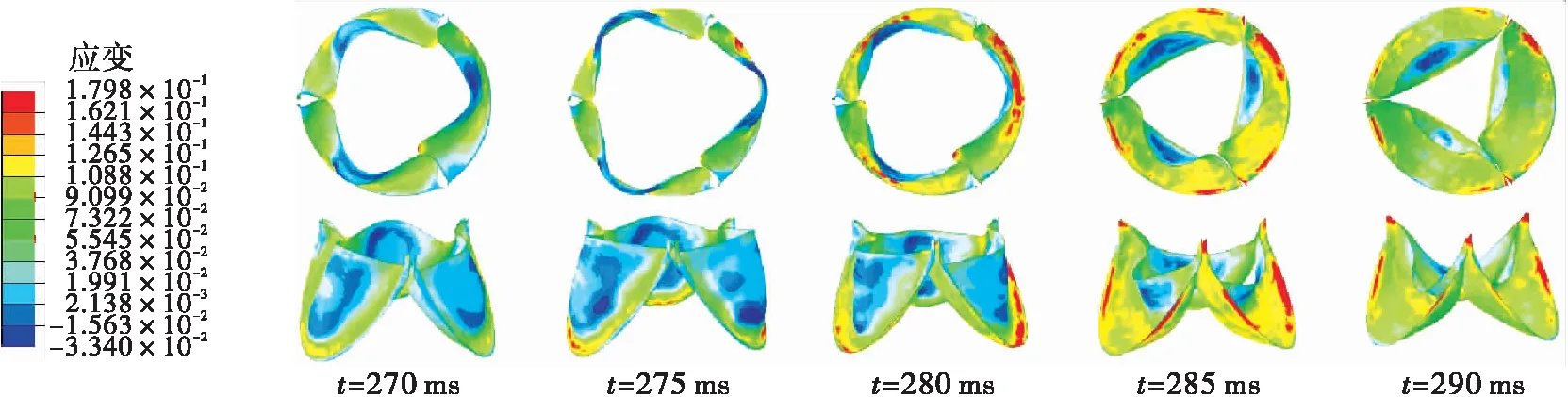
(b)仿真D1

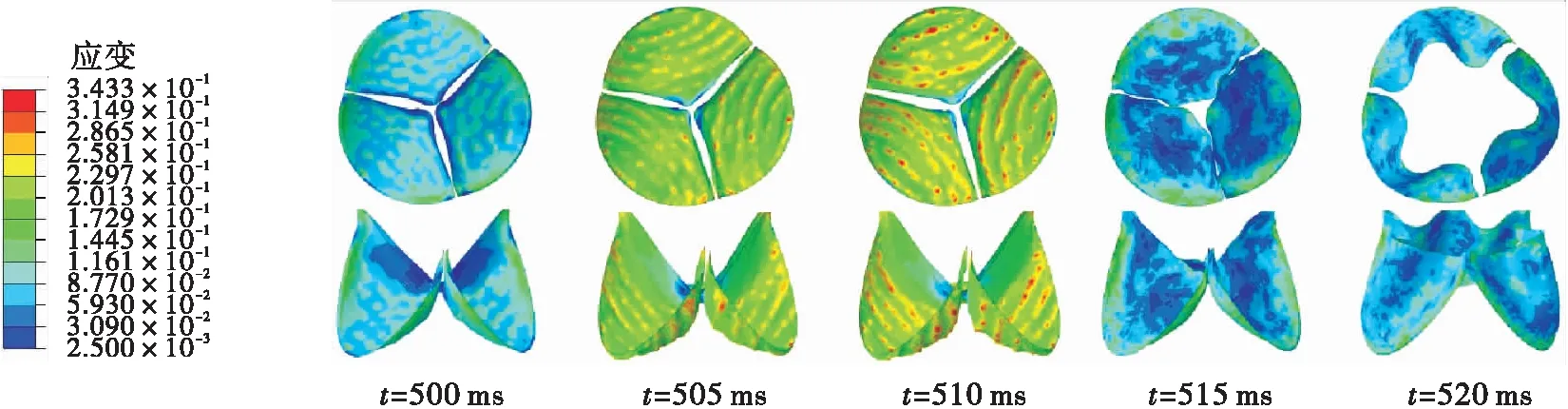
(c)仿真D2

为了进一步分析瓣膜不同区域的受力情况，本文还分析了碰撞过程中不同分区的平均应力变化，结果如图11所示。区域的划分情况见图3(b)。从图11(a)可知，在仿真S1中，瓣膜主体及自由边区域的应力较正常工况下没有太大的改变，但接触边的应力在102～107 ms内明显增大，最大平均应力达到0.369 MPa。从图11(b)可知，在仿真D1中，接触边和主体区域的应力在280～290 ms期间略高于正常工况。从图11(c)可知，在仿真D2中，瓣膜上各区域的应力都远大于生理压力下的应力值，并且具有相似的变化趋势，在506 ms时达到最大平均应力(为3.907 MPa)。

从仿真结果来看，在射血期和舒张早期进行胸部钝性冲击时,瓣膜都没有产生较大的应变，而在舒张中期的碰撞使得主动脉瓣产生巨大的应力和应变。推测瓣膜的碰撞响应可能与碰撞时刻瓣膜的初始形态(开或者关)有关。当瓣膜在碰撞时刻处于开启状态时(仿真S1和D1)，较大的有效开口面积可以使更多的血液来回通过瓣膜，尽快地平衡瓣膜两侧由碰撞引起的压力差。当碰撞发生在舒张中期时，主动脉内血压远高于左心室，瓣膜的初始形态是关闭的。主动脉内产生的高压血液持续作用在瓣膜上，产生了较大的应变。这个结果与从尸检结果中推测的结论大体一致，均认为主动脉瓣的钝性冲击损伤更容易发生在舒张期[5- 7]。

(a)仿真S1

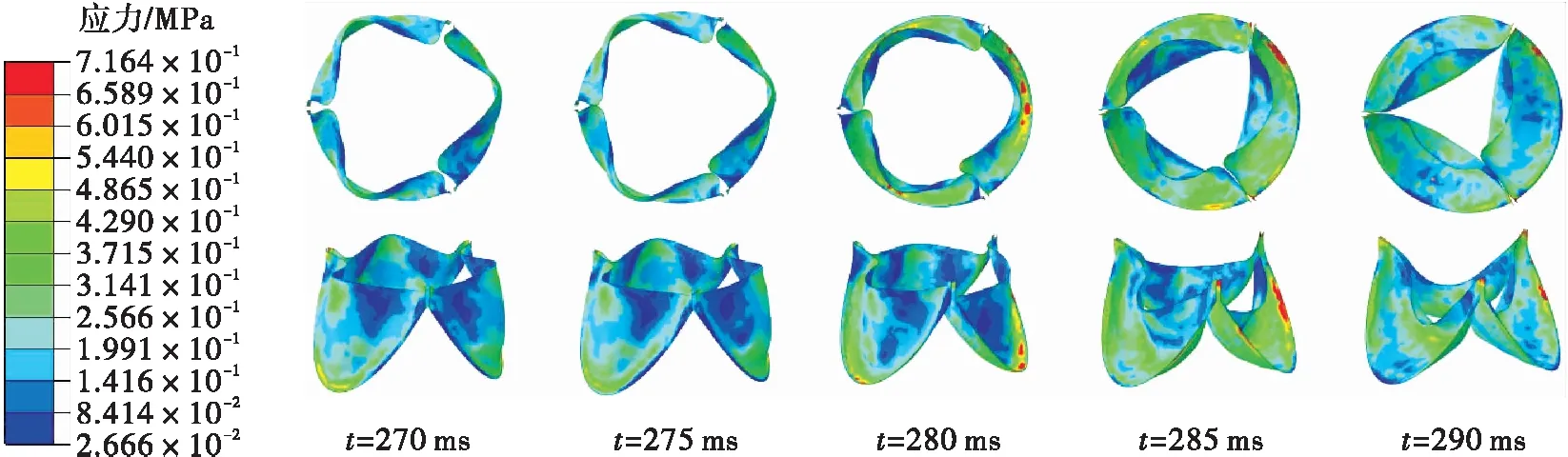
(b)仿真D1

(c)仿真D2

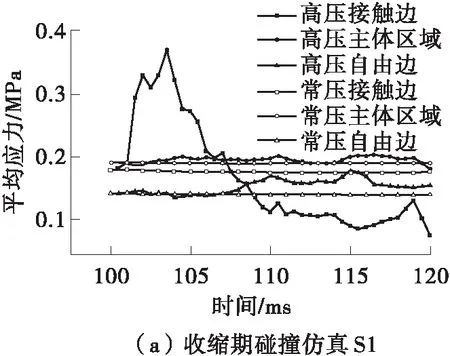
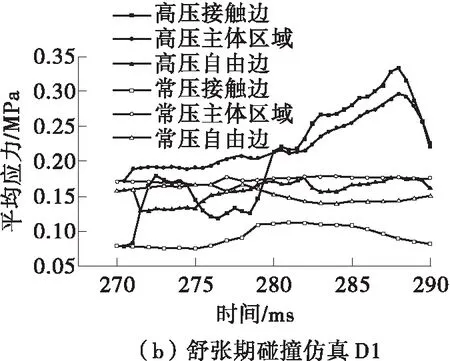
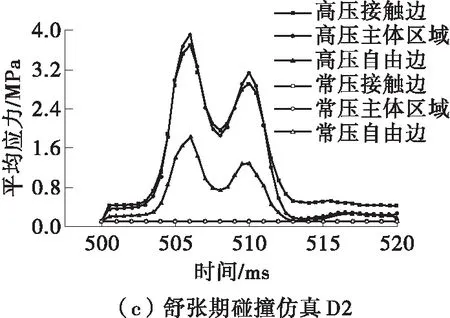
图11 瓣膜不同区域的平均压力变化

4 结论

为了获得主动脉瓣在不同胸部碰撞时刻下的损伤响应规律，本研究建立了主动脉瓣与血液的FSI模型，开展了胸部钝性冲击时刻对主动脉瓣动力学响应的研究，得到如下结论：

(1)引入SPH方法建立的主动脉瓣-血流FSI模型，有效地解决了流体域畸变以及碎片化带来的全过程求解困难和计算不稳定问题，并得到了人的正常心动周期下的实验验证，为动态血流条件下的瓣膜结构的动力学响应分析提供算法基础。

(2)将活体动物不同时刻碰撞的实验结果与人体生理压力变化相结合，可有效确定动态血流边界条件，解决了心动周期内对任意时刻生命特征捕捉的关键问题，成功模拟不同冲击时刻的主动脉瓣动力学响应。

(3)从不同冲击时刻对主动脉瓣动力学响应的影响分析可知，胸部钝性冲击下瓣膜的损伤风险与碰撞时刻瓣膜的开关状态相关性强。当瓣膜在开启状态(如收缩中期)受到冲击时，会加速瓣膜的关闭过程，但瓣膜上的应力应变较小，损伤的几率较低；当瓣膜在关闭状态(如舒张中后期)受到冲击时，瓣膜的运动学响应变化不大，但产生了很大的应力和应变，增加了损伤风险。

本文的定量分析结果为瓣膜的钝性冲击损伤机理研究提供了理论基础，对汽车乘员保护研究及航空航天领域乘员舱的安全设计具有重要的意义。