面向非随机缺失数据的协同过滤评分方法

古万荣 谢贤芬 张子烨 毛宜军† 梁早清 何亦琛

(1．华南农业大学 数学与信息学院，广东 广州510642； 2.暨南大学 经济学院，广东 广州510632；3.华南理工大学 数学学院，广东 广州 510640)

随着互联网电子商务的发展，推荐系统显得日益重要。直接使用推荐结果，用户可以减少浏览时间、提升网购的满意度，商家可以提高转化率和利润率。自Netflix奖金设立以来，推荐技术的研究尤其在协同过滤算法方面的研究日益被学术界和工业界所关注[1]。

目前大多数推荐技术的研究都基于用户历史行为，或融合一些上下文因素，如时间周期、点击间隔等[2- 3]，比较少对用户和物品的协同矩阵的内在结构进行深入理解和剖析。因此，大多数推荐算法都是基于模型或基于近邻方法，利用评分预测矩阵等代数工具进行挖掘。这些方法大多基于这种假设：评分预测矩阵的缺失或用户物品关联的缺失是随机的。这种假设使得各种评分预测方法倾向于将已有数据和预测数据看作是同一分布的，这并不符合电子商务或社交网络中的兴趣组和社群分块的实际情况。因此，目前对推荐系统的研究仍然存在至少3个方面的问题：①关联数据的稀疏性[4]。这是在大数据挖掘中普遍存在的一个特点，在推荐系统研究中，这个问题也始终没有得到很好的解决。稀疏性使得轻微的变动或计算误差将导致结果的剧烈变动。②关联矩阵规模庞大导致算法可扩展性差[5]。在推荐系统中，许多算法依赖于关联矩阵的更新，每一次更新都要将关联矩阵重新计算或分解，由于关联矩阵较大，计算的复杂性导致这些研究成果很难在应用系统中使用。③算法缺乏对不同用户社区群的区分[6]。这就导致了有些具备特殊需求的用户长期得不到正确的兴趣挖掘，影响了整体推荐精度。

基于内容的推荐的基本原理在于挖掘用户的历史行为所关联的物品内容，即与内容是相关的[7]。基于协同过滤的推荐方法不需要分析内容，即通过用户和物品的协同关系来确定给定用户可能感兴趣的物品列表[8- 9]。由于纯基于内容的推荐方法实际上是将推荐预测的关联性看作是非随机的，因此，这就容易解释为什么很多应用使用基于内容的方法比单纯使用协同过滤方法的准确度要高。协同过滤方法是推荐算法的另外一类算法，主要原理是通过用户和物品的关联协同性进行基于经验或基于模型的推荐预测。矩阵分解方法在推荐技术的研究中因具有很高的推荐准确度而受到学术界的广泛关注[10]。经典的方法有奇异值分解(SVD)法[11]和NMF非负矩阵分解(NMF)法[12- 13]。在理论研究上，矩阵分解方法可以有效地挖掘用户和物品之间的潜在关联因素，预测的精度较高。在推荐系统实践中，每次用户新购买或点击时，将会对原始的用户和物品的二分图产生影响，即原始关联矩阵将会改变。在线系统中，用户购买物品的关联动作以及用户评价物品的评分矩阵是动态变化的。随着每一个数据的细微改变，都需要对相应的矩阵进行分解，导致该类算法很难在实际系统中得到应用[14]。此外，由于缺失数据的非随机性，出现了不同兴趣聚集和社团聚集现象。为此，如果能只对矩阵的局部变化做出局部分解，既能减轻计算负担，又能有效挖掘非随机缺失的评分数据，从而使该类算法在较准确的预测率情况下应用到实际的大型推荐系统中[15- 17]。在应用系统开发中，也有人提出了间隔性增量式的分解，即不对用户的每一个动作做出即时的分解应答。这种做法虽然缓解了运算负担，但从本质上来说是以推荐模型的时效性作为代价的，而且仍然没有解决全局矩阵分解的大量运算问题。

在算法优化方面，文献[18- 19]提出了使用矩阵聚类的方法来提高算法的效率，以提高应用的可扩展性。这类方法的基本原理是先对用户或物品的行列向量进行聚类，然后以聚类为单位进行计算，从而缩小了运算的规模和粒度。也有算法[20]提出了同时对行列向量进行聚类，这样进一步缩减了后续计算的规模，具有一定的效果。这类方法在应用中具有较强的可扩展性，但规定了某用户或某物品只能属于某一个类别，这跟实际情况并不完全符合。因为在现实的电子商务环境中，用户或物品往往从属于多个类，即便是从属于同一个类，参与度也不能对等看待。

在社交网络的研究中，基于图的社区发现可以等价表示为关联矩阵的近似双边块对角结构[21- 22]。基于此思想，本文基于评分缺失非随机性假设，提出了先将用户和物品的评分矩阵转化为近似双边块对角矩阵，再在近似双边块对角矩阵上运用矩阵分解方法进行评分预测的方法，并运用协同过滤算法验证其有效性。

1 基于矩阵分解的推荐技术

推荐技术的研究往往集中于用户和物品之间的协同关系，最后预测用户和物品之间的兴趣关系。一般有Top@n推荐和评分预测两种应用问题。一般而言，Top@n推荐的研究需要建立用户和物品之间的兴趣度函数，以计算特定用户对特定物品之间的兴趣度或购买意愿。评分预测问题也可称为缺失评分填补问题或矩阵填补问题，常使用代数上已证明的矩阵分解方法来获得填补值。

矩阵分解一般是指将一个矩阵，即推荐系统中的评分预测矩阵，分解为两个或多个矩阵的乘积。在物理意义上可以理解为，用户对物品的喜好，都是基于对物品的特殊因子的喜好，不同的因子有不同的权重，对于新物品，如果它具有用户喜好的因子，则该物品被推荐的概率更大。矩阵分解式如下：

(1)

那么问题就转化为如何求得Pm×k和Qk×n矩阵中的元素问题，该问题可以通过转化为回归问题来解决。对于Rm×n矩阵中的每个元素，可以表示为如下形式：

(2)

2 矩阵分块变换

2.1 基本定义

为了方便说明问题，本文将给出双边块矩阵的相关通用定义。

定义1(双边块对角矩阵) 矩阵X被称为双边块对角矩阵，当且仅当该矩阵可以通过变换变成如下形式：

(3)

定义2(近似双边块对角矩阵，ABBDF) 当矩阵X只存在若干个非0值时，称矩阵X是一个近似双边块对角矩阵，通过行或列变换可以变成如下形式：

(4)

与定义1相比，定义2多了一个“近似”的表述，即近似双边块对角矩阵允许包含一些非0值的散点。

2.2 分块矩阵变换算法

在社区发现的研究中，高密度聚集的社区意味着兴趣爱好相似。高密度的社区可以为下一步基于矩阵分解的协同过滤评分预测提供数据基础。为清晰起见，本文提出了精确双边块对角化转换和近似双边块对角化转换算法。

(1)精确矩阵分块算法

在双边块对角化的变换过程中，基本操作就是迭代执行行和列的交换，使之形成双边块对角化形式。其中一个重要的步骤就是将某些行或列向量排列到双边。

该过程等价于在用户和物品的关联二分图中基于点割集的分割。一般而言，一个图的点割集可能有很多个，因此最优化的方式是找到最小的点分割集。在图论研究中，已知找最小的点割集是NP难问题。由于该问题的求解具有实际应用意义，因此人们提出了许多基于启发式的方法来实现图的点分割，如基于层次分析、谱分析和基于核函数的方法等。

本文算法在获得矩阵对角化时，将使用到子矩阵密度，单层双边块对角矩阵和对角块的平均密度计算方法为GetDensity(X,G)。该算法描述如下：

GetDensity(X,G) //获取密度

{输入：评分矩阵X及其二分图G(V,ε)=(R∪C,ε)，V=R∪C，R和C分别是行和列的集合。

Γv←{V1,V2,…，Vk；Vs}←GP(G)；

//使用点割集函数GP( )获得分割集

将矩阵X的行按R1R2…RkRs的顺序排列；

将矩阵X的列按C1C2…CkCs的顺序排列；

//根据行列排序后，Di互不相交

//Di对应的顶点集是Vi=Ri∪Ci}

在该算法的迭代过程中，应尽量让排列后的对角块的平均密度高于原始矩阵密度。

双边块对角化变换算法描述如下：

TwoSideBlock(X,G,ρ) //双边块对角化变换

{输入：目标密度ρ、评分矩阵X及其二分图G(V,ε)=(R∪C,ε)，V=R∪C，R和C分别是行和列的集合。

输出：排列好的双边块对角矩阵X。

ρX←ρ(X)； //将矩阵平均密度用ρX保存

ifρX<ρthen

//当平均密度小于预设目标密度ρ时

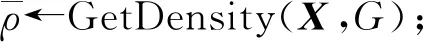
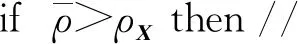
TwoSideBlock(Di,GVi,ρ)；

//对每个对角块Di递归调用变换函数

end

end

end}

在该算法中，目标密度ρ需要在函数调用时设定。当算法迭代计算达到这个阈值时终止。该阈值如果设置过高，则可能会导致迭代计算不会停止，针对这一问题，可以通过对迭代次数进行控制：在代码中针对迭代次数设置一个计时器，当迭代次数超过给定阈值时，不管密度是否达到目标值，都停止迭代。

(2)近似矩阵分块算法

与精确双边块对角化算法不同，在近似对角块变换方法中，本文通过抽取向量到边上来进一步提高密度，直到密度达到要求或迭代次数超过预设值。算法描述如下：

ApprTwoSideBlock(X,G,ρ)

//近似双边块对角化变换

{输入：目标密度ρ、评分矩阵X及其二分图G(V,ε),V=R∪C，R、C分别是行和列的集合。

输出：排列好的近似双边块对角矩阵X。

ifρX>ρthen

//当平均密度大于目标密度时，算法终止

return;

else

Γe←{V1,V2,…,Vk}←GP(G)；

//使用点割集函数获得分割集

将矩阵X的行按R1R2…Rk的顺序排列；

将矩阵X的列按C1C2…Ck的顺序排列；

//根据行列排序后，Di互不相交

{V′1，V′2,…，V′k;V′s}←ImprGetDensity(X,

G,Γe)；

//使用改进的密度函数生成分块集

for每一个对角块Dido

ApprTwoSideBlock(Di,GV′i,ρ)；

//对每个对角块Di递归调用近似分块算法

end

end}

该算法调用了ImprGetDensity(X,G,Γe)函数，该函数是改进的密度计算方法。该函数从对角块中选一处最大限度提高平均密度的向量并移动到边。最简单的做法是逐个穷举移动，并计算平均密度值，选取最大限度提高密度的移动方法。但在实际应用中，往往是专注于最小密度向量，即对子对角块中具有较少非0的向量进行缓存。改进的密度计算算法描述如下：

ImprGetDensity(X,G,Γe)

{输入：评分矩阵X及其二分图G(V,ε)，以及图G(V,ε)中的GP(G)函数的运算结果Γe，V=R∪C，R和C分别是行和列的集合。

输出：更好地提升密度的图分割结果Γ′。

{V′1，V′2,…，V′k;V′s}←{V1，V2,…，Vk;θ}；

//将目前的分块用临时变量存储

whileρ(D1,D2,…，Dk)<ρ(X)do

//当目前的分块平均密度小于整个矩阵密度时

for每一个对角块Dido

forDi的每一个行和列向量 do

//对每个对角块Di及其行列向量进行迭代

//选择对角块移除后的块平均密度,n(D)为D的非0个数，x(D)为D中对角块的非0个数，area(D)为D的区域个数。

//记录相关信息

end

end

end

将x′向量交换到双边;

V′i′←V′i′-{node(x′)};//从V′i′中移除相关节点；node(x′)为V′i′中对应向量的第i′个节点

V′s←V′s∪{node(x′)};

//将相关的节点加入到V′s中

end

returnΓ′←{V′1，V′2，…，V′k;V′s};

//记录分块信息并返回。}

2.3 基于分块矩阵的协同过滤

矩阵分解算法的执行并没有限定矩阵形态，因此将用户和物品的关联矩阵或评分矩阵进行转换后，仍然可以使用基于矩阵分解的协同过滤评分预测方法。也就是说，矩阵变换前后，其物理特性并没有改变。但在矩阵分解挖掘过程中，对具有高度兴趣社群聚集的分块子矩阵进行分解挖掘，可以更聚焦于特定兴趣的用户群，减少全局无关因素干扰，同时也提高了评分预测的整体处理效率。假设只有单核处理器对数据进行处理，矩阵分块后规模变小，子矩阵分解时间呈指数级下降，虽然需要依次处理多个子矩阵，但多个子矩阵的轮换处理仅仅增加线性倍数时间。综合考虑，本文采用先分块再进行分解的方法仍然具有很大的效率优势。双边块对角矩阵的基本结构如图1所示。

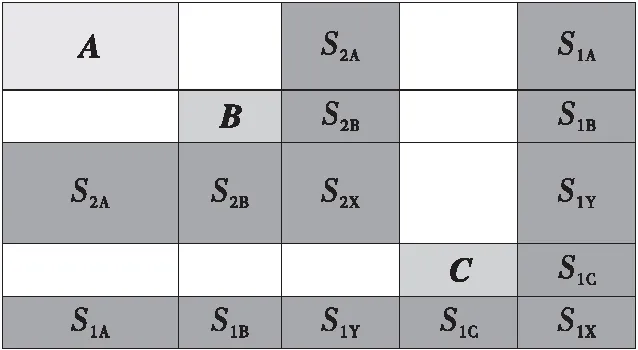
图1 双边块对角矩阵的基本结构

如图1所示，对于每一个对角块，可以通过双边拼接方法来重建子用户物品群，即可以通过挑选部分用户和物品及其关联集合来进行协同过滤推荐预测。例如可以通过A、B、C对角块重构3个子矩阵，并忽略在非对角块上的零星非0值点，结果如图2所示。

图2 根据双边块对角型矩阵抽取的子矩阵

令X∈Rm×n为一个稀疏矩阵，U∈Rm×r，V∈Rr×n，则矩阵分解算法可以形式化表示为P=(f,Dw,C,R)，其中，预测函数f是自变量和因变量都是m×n的矩阵：Rm×n→Rm×n；数据权重矩阵w∈Rm×n；Dw(X,f(UVT))≥0为损失函数，用于记录预测值f(UVT)和原始值X之间的误差；C为对分解后的矩阵U和V的约束；R(U,V)≥0是正则化项。因此，在矩阵分解模型中，需要求解以下优化函数：

其中，函数D(·,·)返回值是评分预测矩阵中各个元素的评估损失的累加和。

3 实验与结果分析

3.1 实验数据集

在本文实验中，使用了公测数据集MoiveLens- 100K(ML100K)和MovieLens- 1M(ML1M)、雅虎音乐数据集(YM)以及大众点评数据集(DP)，如表1所示。这些数据集都遵循着观看或购买后才可以点评的较高评分门槛，因此具备一定的兴趣社群特性。例如，一个用户观看电影有一定的偏向性，因此他缺失的评分就具有非随机的特点。

3.2 参数调整及分析实验

不同的目标密度会对生成的分块矩阵有不同的分布结果，对协同过滤评分预测精度也具有重要的意义。如果目标密度设置过低，则有些用户和物品的关联社区群不能充分挖掘出来；如果目标密度设置过高，则会出现较多零散社区群，也同样不利于协同过滤预测。目标密度ρ与对角块个数的关系如图3所示。从图中可知：随着ρ的增大，精确双边块矩阵的对角块个数会增加，然后进入平稳状态，其直观的原因是，当目标密度达到一定的上限后将无法再上升，即无法再进行变换；近似双边块矩阵的对角块个数基本上随着ρ的增大而增长，说明通过将低密度的行或列移动到双边来可进一步提升密度。

表1 实验使用的数据集

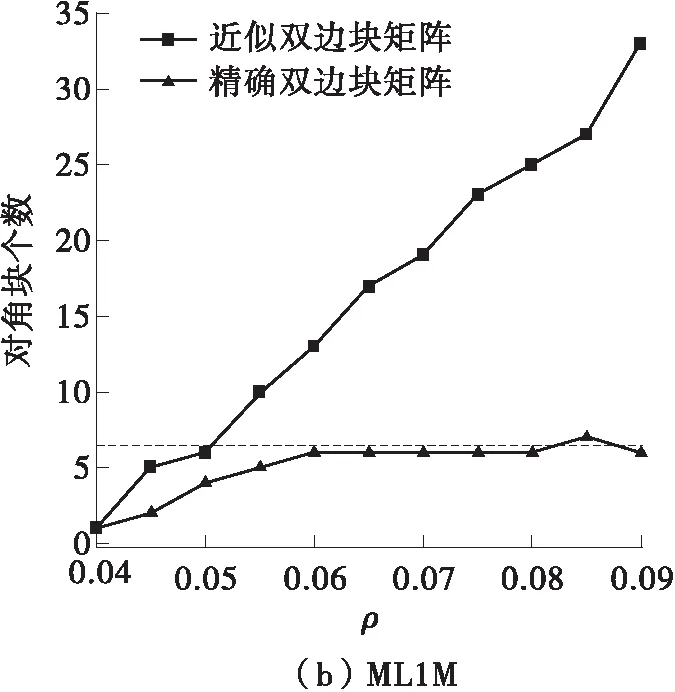
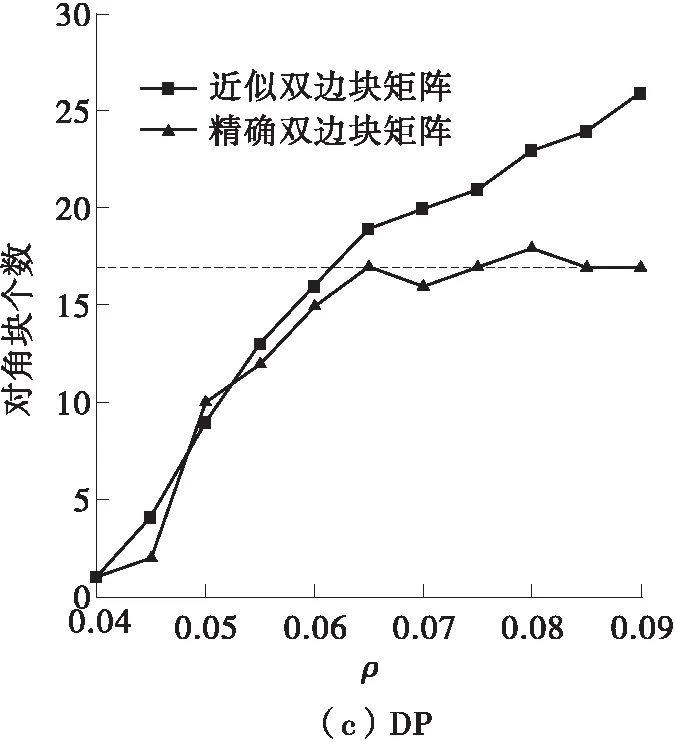
图3 不同数据集的目标密度与对角块个数的分布统计

3.3 实验结果分析

本文实验采用了10折交叉验证，即将实验数据切分为10份，其中1份作为测试集，另外9份作为训练集，然后轮换其他另外1份作为测试集，剩余的作为训练集，轮询重复10次后，获得的准确度平均值作为实验最终结果。

在矩阵分解算法中，分解因子的个数是预先设定的。如果该个数太小，则不足以近似表示原始关联矩阵的有效信息；如果该个数太大，一方面模型复杂耗时，另一方面容易产生过拟合问题。

表2 ML1M的对角块数据

目标密度取不同值时对预测精度的影响如图5所示。从图中可知，理想的目标密度参数随着数据集的不同而不同，每条虚线以下的曲线部分表示RMSE较小，意味着评分预测的准确度较高，反之，在虚线以上的曲线部分则表示RMSE较大，预测的准确度较低。因此，通过合适但并不苛刻的密度设置，本文方法可以提升评分预测的精度。但目标密度的设定需要遵循合适的经验规律，目标密度设置过高会导致预测精度降低。其直观的原因在于，本文方法在密度设置过高时会形成较多的零散碎块，从而影响最终的矩阵分解的评分预测准确度。

图4 评分预测准确度和因子个数的关系

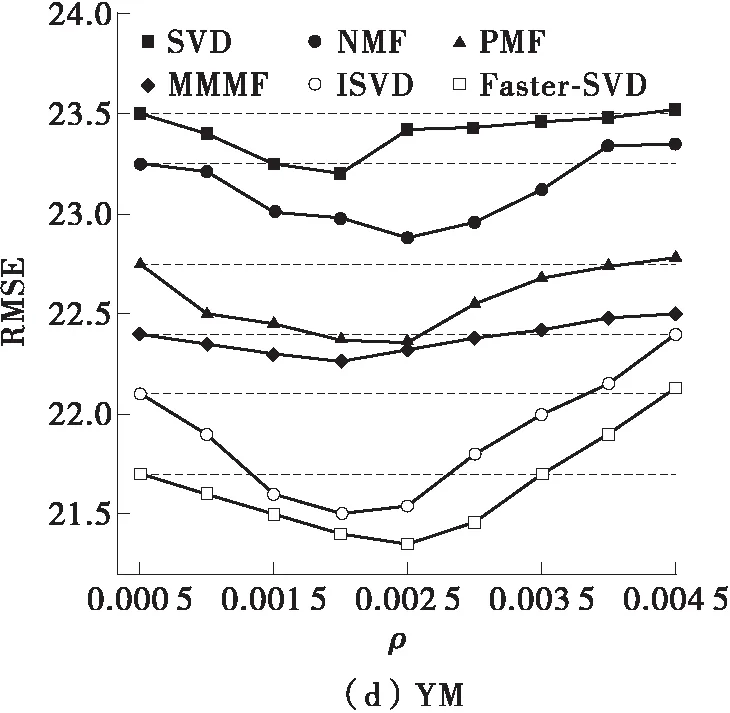
图5 目标密度和预测精度的关系

表3 ML1M在不同目标密度值下的对角块统计

本文方法先对用户和物品的评分矩阵进行近似双边块对角化变换，再对对角块进行单独的矩阵分解。这样做的好处在于：①可以局部进行矩阵分解，因此当用户单独对物品进行购买或评分后，推荐系统无需针对整个关联矩阵进行计算；②可以对每个对角矩阵进行分布式处理，从而提高推荐系统的并行化效率。本文方法的步骤如下：

1)将关联矩阵X转化为一个多层双边对角矩阵；

2)将原始矩阵切分为8个对角块，对每个对角块利用独立的处理核进行分解，使其互不干扰；

3)基于分解结构将其合并为近似预测原始关联矩阵。

在实验中记录每个步骤所消耗的时间，并统计其分布式系统的加速比(对近似双边块对角矩阵的分布式分解与对原矩阵的直接分解的运行时间之比)。为了方便对比分析，每个矩阵分解因子和前面实验相同，即r=60。实验结果如表5所示。

表4 各种矩阵分解方法的参数和预测结果

表5 各种矩阵分解方法的实验结果

从表5可知，本文提出的近似双边块对角矩阵对分布式处理具有显著的加速效果，其原因在于双边块对角矩阵可以直接拆解，互不影响，这在推荐系统应用的海量数据处理中具有重要的现实意义。经典的矩阵分解算法(SVD、NMF、PMF和MMMF)比ISVD和Faster-SVD具有较高的加速比，其原因可能是经典算法的辅助处理步骤较少，可较大限度解决单纯使用基于分而治之思想进行分布式计算带来的重复计算问题。但不失一般性，本文提出的分块方法仍然可以很容易应用于分布式处理中。

4 结论与展望

为有效挖掘用户兴趣社群，降低矩阵分解或其他协同过滤算法的运算时间，本文基于缺失评分的非随机性特点，提出了先将用户和物品的评分矩阵变换为近似双边块对角矩阵，再对对角块进行单独的矩阵分解的方法。在公测数据集上的实验结果表明：基于双边块对角变换的矩阵分解方法具有更高的评分预测精度，应用在分布式处理中具有较高的加速比和良好的可扩展性。本文提出的方法的主要优点如下：

(1)本文方法先将原始矩阵变换为分块的矩阵，从而可以针对密度聚集的子矩阵进行深入分析，有效挖掘用户兴趣社群并缓解数据稀疏性的影响；

(2)本文方法的局部计算特性，使得实际系统的数据更新不需要对整个大矩阵进行重新分解，只需要在更新点所在的高密度块进行处理，从而提高了应用的可扩展性；

(3)各高密度子矩阵的协同过滤和矩阵分解互不影响，使得算法的生成矩阵更容易并行化，提高了整体系统的预测效率。

未来将深入研究基于分块的矩阵分解的其他协同过滤算法，使得现有应用系统能无缝对接本文方法，从而实现其应用扩展。