基于糖尿病性视网膜病变数据集的支持向量机优化算法比较

张 颖，窦一峰

（天津市宝坻区人民医院泌尿外科1，网络信息中心2，天津 301800）

糖尿病性视网膜病变的计算机辅助判别问题是医学信息学上的重点课题，作为机器学习中有监督学习的代表，支持向量机算法在小样本、低维空间和线性模式下对分类问题的预测性能表现较好，而支持向量机中的惩罚参数c 以及径向基核函数中的参数g 的选择则决定了该而分类算法的分类精度和预测性能。目前主要有5 种对上述两个重要参数的寻优方法，即经验选择法、网格选择法[1]、遗传优化算法[2]、粒子群优化算法[3]、遗传或粒子群与模拟退火法[4]相结合的算法。既往基于支持向量机的改进算法在糖尿病性视网膜病变数据集上的性能研究较少，基于此，本研究选取支持向量机算法作为基础模型，利用参数优化的思想对不同改进算法在糖尿病性视网膜病变数据集上的分类效果进行比较研究，以期为机器学习算法在辅助临床诊断决策方面提供一定的参考依据，现报道如下。

1 资料与方法

1.1 数据来源 采用由匈牙利德布勒森大学的学者Balint Anta 博士提供糖尿病性视网膜病变数据集[5]进行实验研究。糖尿病性视网膜病变数据集包含1151 个实例共20 个属性，均是从Messidor 图像集中提取的特征，来预测图像是否包含糖尿病性视网膜病变的体征，具体信息见表1。

1.2 支持向量机算法原理 支持向量机算法（support vector machine，SVM）是由Vapnik VN[6]在1995 年提出的，算法的基本思想是通过非线性变换将输入数据映射到一个高维空间中并建立最优线性分类面，将两种样本类别进行正确的分类。支持向量机模型基于结构风险最小化原则，通过计算最优超平面（optimal separating hyperplane，OSH）[7]来进行分类的统计方法，最优超平面之间的间隔越大证明建立的支持向量机模型的推广能力越强。假定大小为l 的训练样本集{（xi，yi）,i=1,2,...,l}，其数据样本仅可以被分成2 类，假设xiϵRN属于第1 类样本，记为正值（yi=1），否则属于第2 类，记为负值（yi=-1），此时需要构造一个判别函数，使得该函数能够尽可能正确的对测试数据样本进行分类。

表1 糖尿病性视网膜病变数据集

如果存在分类超平面

将此时的训练样本集称为是线性可分的，其中将w·x 称为向量和向量xiϵRN的内积，公式（1-1）和公式（1-2）中的wϵRN，bϵR 都进行了规范化处理。对于公式（1-2），可改写成如下形式：

根据最优超平面的定义可以得到如下判别函数

其泛化能力最优，其中sign(·)为符号函数。最优超平面的求解需要最大化2/‖w‖，即最小化‖w‖2/2，因此可以将其转化成下面的由目标函数和约束条件组成的二次规划问题：

当训练样本集为线性不可分的时候，需要引入非负参数，即松驰变量ξi，i=1,2,...,l，此时的分类超平面的最优化问题就转换成如公式（1-6）所示的形式。

其中c 为约束参数，也叫做惩罚参数，c 的值越大则说明对错误分类的惩罚力度越大。利用拉格朗日乘子法进行求解可得

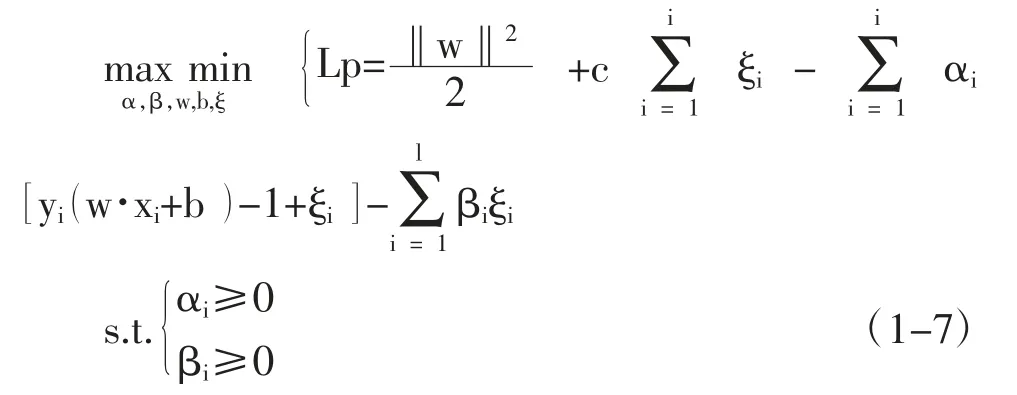
其中αi和βi表示拉格朗日乘子，进一步可得

将公式（1-8）～（1-10）代入到公式（1-7）中，得到对偶的最优化问题形式：

最优化求解得到的αi可能是（a）αi=0；（b）0＜αi＜c；（c）αi=c。由公式（1-8）可知，只有支持向量对最优超平面和判别函数有正向作用，所对应的学习方法才叫做支持向量机算法。在支持向量中，（c）所对应的xi称为边界支持向量（boundary support vector，BSV），实际上就是被错分的训练样本点；（b）所对应的xi称为标准支持向量（normal support vector，NSV），根据Karush-Kuhn-Tucher 条件[8]可知，在最优样本点时，拉格朗日乘子与对应的约束之间乘积等于0，即

对于标准支持向量（0＜αi＜c），由公式（1-10）得到βi＞0，因此，由公式（1-12）可得βi=0，由此可知，对于任一标准支持向量xi均满足

从而计算参数b 为

对所有标准支持向量分别计算b 的值，然后对结果求平均值，可得

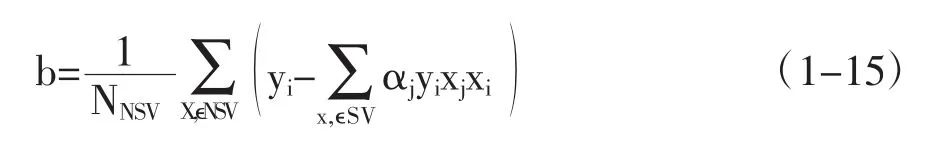
其中，NNSV 为标准支持向量的个数。由公式（1-13）可知，支持向量机模型就是满足公式（1-3）所示中要求的样本数据。

1.3 性能度量 选取数据集均为典型的二分类问题，因此为了更加全面的评价算法的性能，采用多指标评价的方法对算法分类效果进行对比分析，这里引入一个有监督学习二分类评价的混淆矩阵，见表2。

表2 二分类问题混淆矩阵

2 结果

2.1 实验结果 选取在线性模式下对小样本分类较好的支持向量机算法为基础模型，分别采用基于原始的支持向量机、基于主成分分析优化的改进支持向量机、基于网格搜索优化的改进支持向量机，基于遗传算法进行参数优化的改进支持向量机和基于粒子群算法进行参数优化的改进支持向量机。由于支持向量机算法对核的选取不敏感，因此本研究所有实验算法的支持向量机核函数均采用径向基核函数，原始算法和主成分改进算法中的参数c 初始值设置为100，参数g 初始值设置为4，其余算法的参数c 的范围为 [0.1，100]，参数g 的范围为[0.01，1000]，遗传算法和粒子群算法的参数设置见表3。采用MATLAB2016a 作为编程语言进行算法实验，为了更好的进行参数优化算法的性能比较，随机选取糖尿病性视网膜病变数据集的50%、60%、70%、80%和90%作为有监督学习的已标注数据，即训练数据，剩余的数据作为测试数据，实验中每个算法都采用3 折交叉验证方法，报告的实验结果均采用10 次重复独立运行结果的平均值，具体实验结果见表4。

表3 遗传算法和粒子群算法的参数设置

表4 糖尿病性视网膜病变数据集的实验结果

表4 （续）

2.2 参数对比结果 本研究均假定惩罚因子c 的取值范围为[0.1，100]，它主要用来控制分类模型的模型复杂度以及逼近误差的折中，如果惩罚因子c 越大，那么说明该算法对数据的拟合程度越好，但同时也会降低算法的泛化能力，不利于算法的推广应用。同时本研究也均假定所选取的高斯核函数中的参数g 的取值范围为[0.01，1000]，它决定了算法的分类精度。不同训练占比的数据集下，通过网格搜索的参数优化以及利用启发式算法进行参数优化得到的参数结果见表5。训练数据集占比为70%和80%时基于遗传算法和粒子群算法对参数寻优时适应度曲线的变化情况见图1、图2。

表5 参数结果

3 讨论

为更好地探究以支持向量机为代表的机器学习算法在辅助临床诊断决策上所发挥的作用，本研究以匈牙利德布勒森大学的学者Balint Anta 博士提供糖尿病性视网膜病变数据集为例，基于MATLAB软件进行编程，对比了不同的基于参数优化思想改进的支持向量机算法的分类预测效果。

本研究结果显示，基于粒子群算法的改进支持向量机模型在病变分类预测中占有17 项最优值，在训练数据占比为50%和60%上，粒子群改进的支持向量机模型在精确率、总精度、马修斯相关系数、F1得分、分类正确率和AUC 值等6 项指标中均取得了最优结果，在70%的指标上取得了5 项指标最优，说明粒子群算法在全局搜索上的优势比较明显，收敛速度较快且参数较少，这使得它的分类性能最好，而基于遗传算法的改进模型较差是因为遗传算法在搜索时需要经过选择、交叉和变异三步操作，而且需要设置的参数也较多，从而导致其收敛速度较慢，效果不太理想。基于网格搜索优化的改进算法整体上占有12 项最优值，在90%的训练占比数据集上产生了精确率、F1 得分、AUC 值等6 项最优结果，说明其搜索能力和寻优效果也比较令人满意。而基于主成分分析改进的算法可能由于数据集的维度较低，暂时体现不出主成分算法降维的优势，因此其参数优化的分类效果较差。

图1 遗传算法适应度变化曲线图

图2 粒子群算法适应度变化曲线图

此外，本研究中适应度值都是训练集得到的适应度值，最后用测试集得到的分类正确率会比最佳适应度值要大，原因在于本研究采用的是交叉检验，得到的适应度值是经过交叉验证后的最佳适应度值的平均值，值得注意的是适应度值图里的数据集是训练数据，然而分类正确率值用的数据集是测试数据；平均适应度值指的是PSO 分类算法和GA 分类算法的种群适应度值，因此这个结果应该是比最佳适应度值要小一些的，不是每一个粒子和基因都是最好的，与Huang S 等[3]和Tang H 等[4]研究讨论相似。

通过本研究可以看出，这些寻优算法虽有一定的应用并取得一定的效果，但是均存在不同程度的问题，如经验选择法对使用者的经验丰富度较高且对样本的依赖程度较大，缺少充分的理论基础支撑；网格选择法的弊端在对步长的选择，如果步长选择过大容易陷入局部最优，选择过小则会造成计算量过大；遗传优化算法需经过选择、交叉和变异三步，参数设置相对复杂，收敛速度较慢，且容易陷入局部最优解；粒子群优化SVM 参数的优点是收敛速度较快且参数较少，但是也容易陷入局部最优；遗传或粒子群算法与模拟退火法相结合来优化SVM 参数的方法虽然提升了收敛速度，在一定程度上改善了局部寻优能力差的不足，但在一些实际的应用中可能会出现稳定性差的问题。未来的研究方向可以考虑在机器学习领域，探究利用信息融合的思想来进行模型组合，或者以支持向量机算法为基础进行分类器集成的方式来提高糖尿病性视网膜病变数据诊断分类的精度。