DBP 和NA 在发射药中扩散性能的分子动力学模拟

丁银凤，梁 昊，丁亚军，肖忠良

（1. 南京理工大学化工学院，南京 210094；2. 南京理工大学特种能源材料教育部重点实验室，南京 210094）

1 引言

表面钝感是实现发射药燃烧高渐增性的常用途径之一，钝感剂通过扩散作用渗入发射药基体，在发射药表层呈由表及里下降的趋势，以降低燃烧初期的气体生成速率。当前中小口径武器所使用的钝感发射药，主要采用邻苯二甲酸二丁酯（DBP）、樟脑等作为钝感功能组分，取得了较好的弹道效果。但是DBP、樟脑分子量较低，在长时间贮存过程中易迁移，引起钝感剂浓度和分布的变化，对发射药的性能稳定性和使用寿命产生负面影响［1］。为降低钝感剂在发射药贮存过程中的迁移速率，提高发射药的使用寿命，目前高分子钝感剂（聚新戊二醇己二酸酯NA）已成功应用到EI 发射药（改性单基发射药）中，较高的分子量提高了发射药的长储稳定 性［2-4］。

但发射药贮存过程中，DBP 和NA 的迁移现象仍然存在，国内外主要采用显微红外光谱［5］以及激光显微共聚焦拉曼光谱［6］等实验手段测定钝感剂的浓度梯度分布数据，并依据Fick 第二定律的高斯解进行曲线拟合从而得到扩散系数，但存在耗时长、检测不准确、操作复杂等不足。目前，也有国外文献报道Bertrand R 通过等温实验确定扩散系数与温度的关系，并考虑发射药基体膨胀效应的影响，建立方程，利用AKTS-SML 软件预测扩散系数，但目前在非稳定实验条件下（例如老化期间的温度波动、膨胀效应），模拟计算钝感剂在发射药的迁移速率具有一定的局限性，而且对于其扩散的机理也没有研究［7］。

近年来，分子动力学模拟（MD 模拟）已成功应用于含能材料领域，尤其在力学性能［8］、相容性［9］等方面已经取得一系列研究成果，同时MD 模拟也成为预测扩散性能、研究扩散微观机理的有效手段，可以得到扩散运动的直观过程并计算扩散系数［10］。李红霞［11］等采用分子动力学方法模拟增塑剂在丁羟粘合剂体系中的运动，通过爱因斯坦关系式求得扩散系数，再与采用加速老化实验方法计算得到的扩散系数对比，模拟值和实验值基本一致，数量级为10-12m2·s-1。MD 模拟也能够从物质的微观信息角度提供理论支持，还具有耗时短、花费低等优点。

本研究针对发射药贮存过程中钝感剂的迁移现象影响发射药的使用寿命，采用分子动力学方法比较DBP 和NA 两种不同分子量的钝感剂在发射药中的扩散性能及机理，并探究温度、硝化甘油（NG）含量对钝感剂扩散性能的影响，以期为钝感发射药寿命的预估提供理论指导。

2 模拟计算

2.1 物理建模

依据NC（含氮量为13.1%）、NG、DBP 与NA 的化学结构式，利用Materials Studio 软件的Visualizer 模块，分别建立分子模型，相对分子量分别为11273、228、277、3000；然后根据配方组成，利用Amorphous Cell 模块构建含有11 个DBP 分子、5 个NC 分子链组成的DBP/NC 体系，两种组分的质量比为1∶19；另外构建含有1 个NA 分子、5 个NC 分子链组成的NA/NC体系，两种组分的质量比为1∶19；构建DBP/NG/NC、NA/NG/NC 体系，组分之间的质量比见3.1.2 节的表1。所构建的DBP/NC、NA/NC、DBP/NG/NC、NA/NG/NC体系模型见图1。

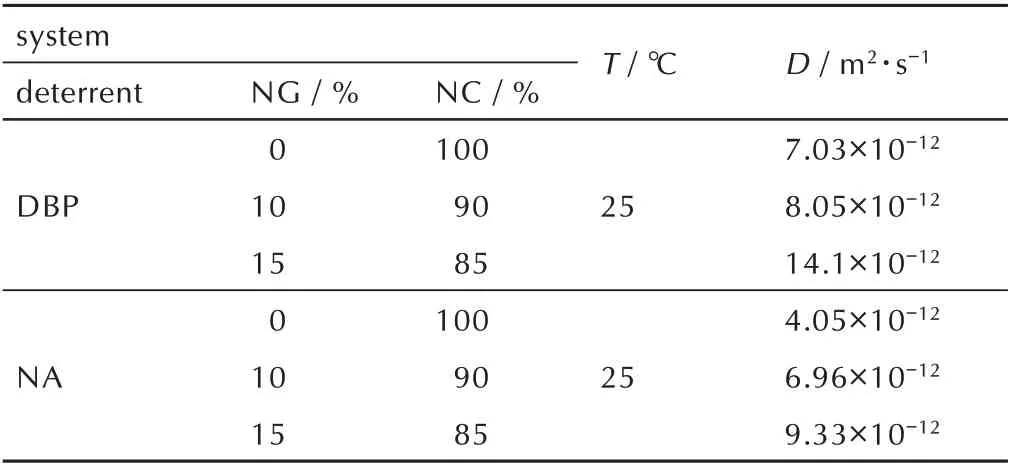
表1 DBP、NA 在双基发射药体系中的扩散系数Table 1 Diffusion coefficients of DBP and NA in double base gun propellant

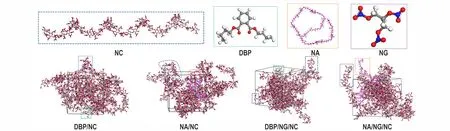
图1 DBP/NC、NA/NC、DBP/NG/NC、NA/NG/NC 体系模型Fig.1 The system models of DBP/NC，NA/NC，DBP/NG/NC and NA/NG/NC

2.2 MD 模拟细节

采用Amorphous Cell 构建DBP/NC、NA/NC 共混体系时，应用周期性边界条件，即以立方元胞为中心，周围有26 个相邻的镜像立方元胞，以达到利用较少分子模拟宏观性质的目的。利用Forcite 模块对建立的体系模型先进行几何优化（Geometry Optimization），几何优化是为了寻找局部最优构型，优化过程均采用Smart Minization 方法，选用COMPASS 立场和Fine 精度，分别用Atom-based［12］和Ewald［13］方法求范德华作用和静电作用；其次利用Anneal 进行若干次退火处理，退火可以使分子跨过局部能垒、寻找全局最优构型，退火的初始温度为300 K、中间温度为800 K、最终温度为300 K，每次退火后自动进行几何优化，这是在全局最优构型中进一步寻找，从中选取能量最低的一帧构型作为输出的最优构型。模拟过程中位能均采用球形截断法，非键截断半径（cutoff distance）取1.5 nm，样条宽度（spline width）取0.1 nm，缓冲宽度（buffer width）取0.05 nm，时 间 步 长 为1fs，采 用Andersen 控温方法［14］和Berendsen 控压方法［15］。

利用Forcite 模块的Dynamic 进行动力学模拟，先运行50 ps 的正则系综NVT（系统的粒子数N、体积V和温度T恒定）进行弛豫，然后选择恒温恒压系综NPT（系统的粒子数N、压强p和温度T恒定），在1 个标准大气压下，分别在5，25，65，85 ℃下进行1000 ps 的MD 模拟，保存全运动轨迹，后400 ps 体系已达到温度和能量平衡（温度和能量随时间的变化率小于5%），选择后400ps 期间的轨迹进行分析均方位移、径向分布函数、自由体积。用同样方法构建DBP/10NG/NC、DBP/15NG/NC、NA/10NG/NC、NA/15NG/NC 体系，并采用同样的参数进行能量优化、MD 模拟。

2.2.1 扩散系数

扩散系数是表征分子扩散迁移能力的重要参数，指的是沿扩散方向在单位时间每单位浓度梯度的条件下，垂直通过单位面积所扩散某物质的质量或摩尔数。分析MD 模拟过程中所得到的粒子的运动轨迹，可以得到均方位移曲线（MSD曲线）。均方位移（MSD）反映模拟体系中分子的空间位置对初始位置的偏移程度，MSD与时间（t）的关系式如方程（1）：

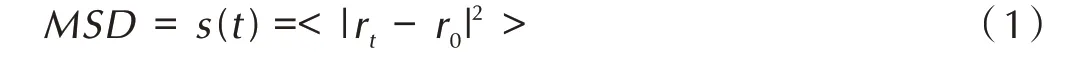
式中，rt表示t时刻分子的坐标；r0表示分子的初始坐标。

通过MSD曲线拟合计算出均方位移-时间斜率（m，m2·s-1），将 其 代 入 计 算 分 子 扩 散 系 数D的Einstein-Smoluchowski［16］方程，如方程（2）：

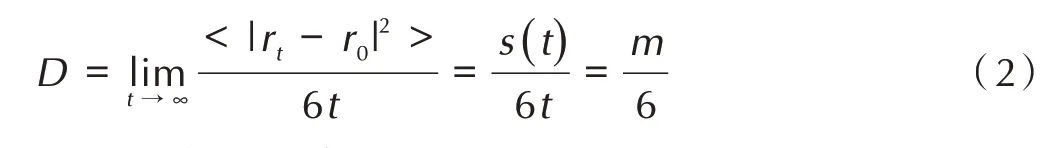
2.2.2 径向分布函数

径向分布函数（RDF）是反映材料微观结构的特征物理量，表示在离所研究原子距离为r处其他原子出现的概率，概率越大，说明这几种原子间的相互作用力越强。通常情况分子间作用力包括氢键和范德华力，氢键长度为0.21～0.31 nm，强范德华力相互作用键长范围为0.31～0.50 nm，弱范德华力相互作用键长大于0.50 nm。从径向分布函数的峰值位置r可以判断相互作用的类型，从峰值g（r）的高低进行推断作用力的强弱［17］。g（r）计算式如方程（3）为：式中，NAB表示与中心粒子A 距离r到r+dr处粒子B 数目；ρ表示粒子B 的平均数目密度。

2.2.3 自由体积分数

体系内的自由体积为分子运动和扩散提供空间，MD 中自由体积表示如方程（4）：

式中，Vf表示自由体积，Vsp表示周期箱体积，Vo表示分子占据体积，单位均为nm3。

自由体积是指除去NC 分子和钝感剂分子共同占据体积后体系的剩余体积，采用Atom Volumes &Surfaces 工具，选取0～0.2 nm 的探针半径，对DBP/NC、NA/NC 体系的自由体积进行计算。因为各体系的总体积大小不一样，为了能够比较这DBP、NA 的相对运动空间，定义自由体积分数FFV［18］为自由体积与各周期箱体积的比值，如方程（5）：

3 结果与讨论

3.1 扩散系数

3.1.1 DBP、NA 在纯NC 体系中的扩散系数

为了探究温度对DBP 和NA 在NC 体系中扩散性能的影响，主要取决于发射药钝感、储存、使用的温度环境，比如钝感温度65～85 ℃，冬天低温0 ℃左右，常温 是25 ℃，所 以DBP/NC、NA/NC 体 系 选 取5、25、65、85 ℃四个代表温度进行MD 模拟，模拟得到的DBP、NA 的MSD曲线，如图2 所示。

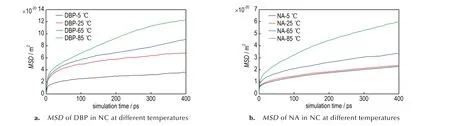
图2 DBP 和NA 在NC 中不同温度下的均方位移Fig.2 MSD curves of DBP and NA in NC at different temperatures

将图2 的MSD曲线进行拟合得到的斜率代入方程（2）求得扩散系数D，结果如图3 所示。从图3可以看出，在相同温度下，DBP 的扩散系数一直高于NA，表明高分子NA 的迁移率低于小分子DBP，这是由于钝感剂分子的大小会影响扩散，分子越小，越容易在聚合物孔洞中跳跃，2 种钝感剂分子的大小顺序为NA＞DBP，这与扩散系数大小的顺序在逻辑上是一致的，即DBP 分子越小，越容易扩散。此外，随着温度升高，DBP、NA 的扩散系数也随着增加，并且DBP 的MSD值随温度的升高的增幅高于NA，尤其65 ℃、85 ℃高温下，DBP 的扩散系数约是NA 的2 倍，比 如85 ℃时DBP 与NA 的 扩 散 系 数分别为3.42×10-11m2·s-1和1.11×10-11m2·s-1。如图4所示，采用指数方程拟合扩散系数D与温度t的关系，t越 高，D的 增 长 趋 势 也 越 大，t无 穷 小 时，D接 近于0。因此，与DBP 相比，NA 具有较好的抗迁移特性，该特性在高温时更为显著。

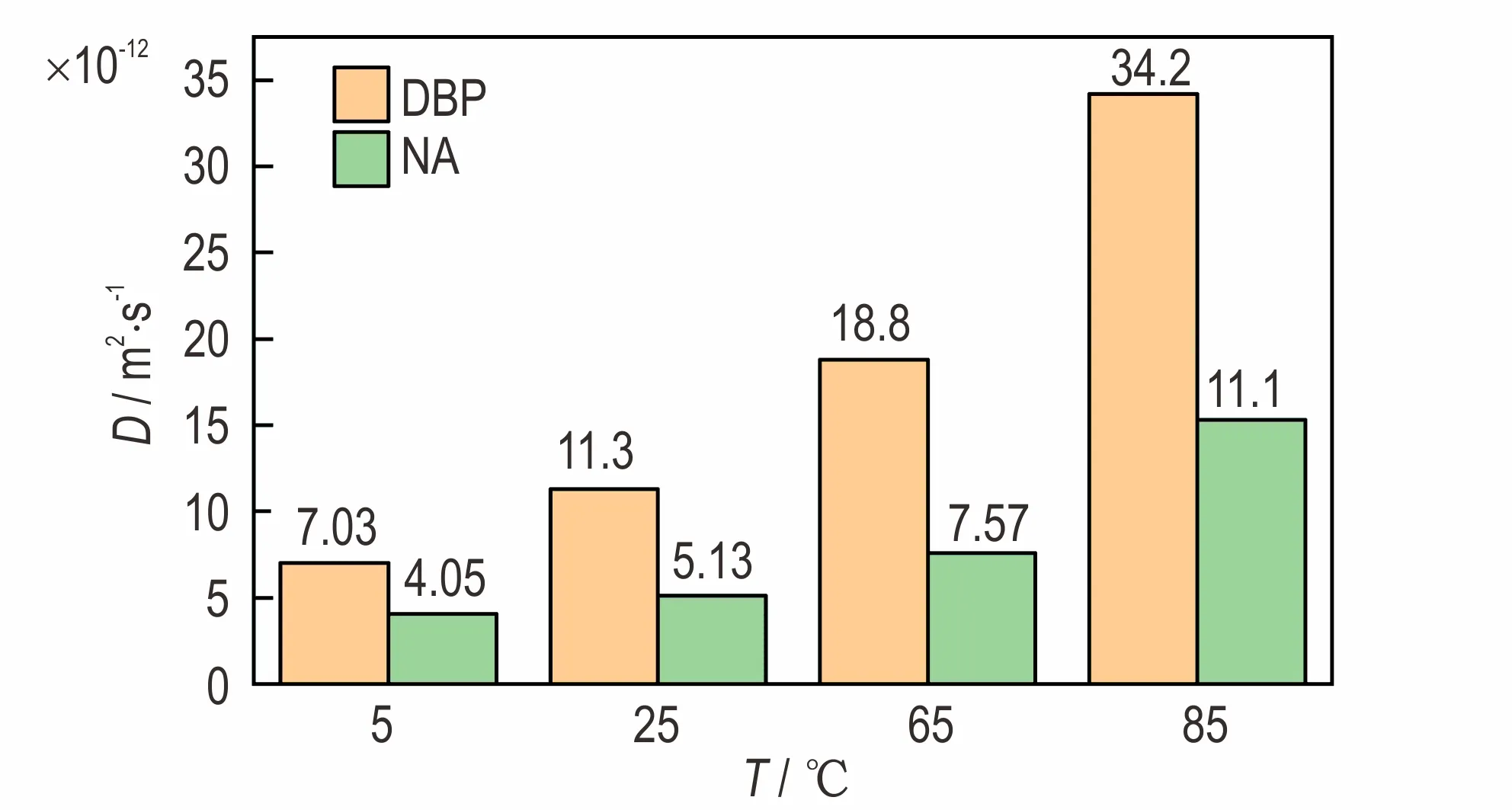
图3 不同温度下DBP 和NA 在NC 中的扩散系数Fig.3 Diffusion coefficients of DBP and NA in NC at different temperatures

3.1.2 DBP、NA 在双基发射药体系中的扩散系数

NG 既是发射药中的能量组分，又对NC 起到增塑的作用，提高加工性能，但NG 的存在也会对钝感剂的扩散迁移产生影响。通常中小口径武器一般用含有10%NG 左右的发射药，所以选取10%，15% NG 含量的双基发射药体系研究NG 含量对钝感剂扩散的影响具有实际意义。外加5%DBP 和5%NA 在双基发射药体系中的物理模型，分别为DBP/10NG/NC、 DBP/15NG/NC、 NA/10NG/NC、NA/15NG/NC 体系，由于温度较多，仅选取25 ℃作为代表进行MD 模拟，得到的MSD曲线如图5 所示。将图5 均方位移随时间的变化曲线，经拟合得到各直线斜率，代入方程（2）计算，得到的扩散系数结果如表1 所示。从表1 中可以看出，在相同温度下，DBP、NA 的扩散系数均随着NG 含量增加而增大，在含有15%NG 的双基发射药体系中运动最快，扩散系 数 分 别 为6.96×10-12m2·s-1和9.33×10-12m2·s-1。因此，提高NG 含量将会加速钝感剂的扩散迁移，从而降低钝感发射药的使用寿命。

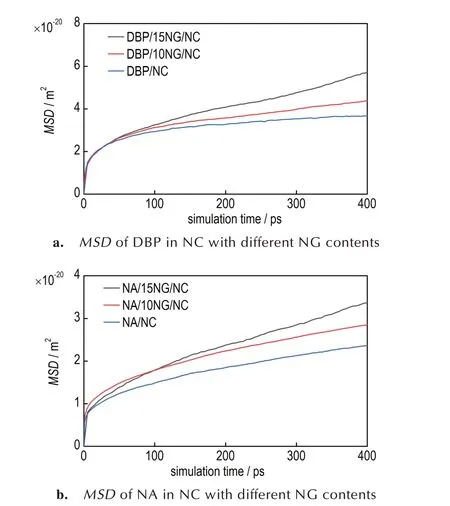
图5 DBP、NA 在双基发射药体系中的均方位移Fig.5 MSD curves of DBP and NA in double base gun propellant

3.2 径向分布函数

为 了 直 观 地 探 讨NC 与DBP、NC 与NA、NC 与NG 之间的相互作用，选取有可能形成氢键作用的NC（O、H、N）与DBP（O、H）、NA（O、H）、NG（H）原子对进行了径向分布函数分析。根据原子的力场类型，NC硝基中的O 原子、H 原子、N 原子分别标记为o12、o2n、h1、n3o，NA、DBP 的O 原子和H 原子都标记为o1=和h1，NG 的H 原子标记为h1，如图6 所示。

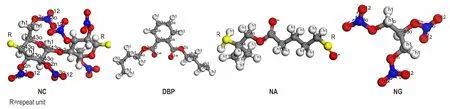
图6 NC、DBP、NA、NG 的原子分布Fig.6 Atomic distrubutions of NC，DBP，NA and NG

3.2.1 DBP、NA 在纯NC 体系的径向分布函数

根据氢键形成的原理，可以推测NC 分子中的h1、o12、o2n、n3o 原子可能与DBP、NA 分子的o1=原子形成氢键，5 种原子对的径向分布函数如图7 所示。

从 图7a 可 看 出，h1（NC）-o1=（DBP）原 子 对 在0.265 nm 附近出现峰，g（r）值为2.27；o2n（NC）-o1=（DBP）原子对在0.315 nm 附近出现峰，g（r）值为2.8；由图7b 看出，h1（NC）-o1=（NA）原子对在0.275 nm附近出现峰，g（r）值为1.96；o2n（NC）-o1=（NA）原子对在0.355 nm 附近出现峰，g（r）值为1.41。表明NC与DBP、NC 与NA 之间存在较强的分子间作用力。

根据图7a 和图7b 的峰值位置r和g（r）的强度，与h1（NC）-o1=（NA）相比，h1（NC）-o1=（DBP）的g（r）峰值更大，表明NC 与DBP 之间的氢键作用比NC 与NA 强。h1（NC）-o1=（DBP）、o12（NC）-h1（DBP）、n3o（NC）-o1=（DBP）、h1（NC）-o1=（NA）、o12（NC）-h1（NA）原子对的g（r）最大时所对应的r值均在0.21～0.31 nm 范围内，表明它们的相互作用力均属于氢键作用力，其它原子对的g（r）最大时的r值均大于0.31 nm，表明它们的相互作用力均属于范德华力。结果表明，NC 与DBP之间的氢键和范德华力均比NC 与NA 之间的大，意味着NC 与DBP 分子间的作用力比NC 与NA 之间的强，表明DBP 更易受到NC 的束缚，从而不利于DBP 扩散。虽然分子间作用力具有阻碍或者减弱扩散的作用，但是DBP 分子量小更容易扩散，通过比较3.1.1 节的扩散系数的结论可知：两者共同的作用结果是分子量影响更大。

进一步分析在不同温度下（5、25、65、85 ℃）NC与DBP、NA 之间的作用力，由于篇幅有限，因此仅选取NC（h1）与DBP（o1=）、NA（o1=）形成氢键作用力最大的径向分布函数进行分析，见图8。

如图8 所示，随着温度的升高，NC 与DBP、NA 的原子间氢键作用的峰值变低，意味着NC 与DBP、NA的分子间作用力减弱，这说明高温使NC 与钝感剂之间的相互作用变弱，因此DBP、NA 扩散速度随着温度的升高而加快。

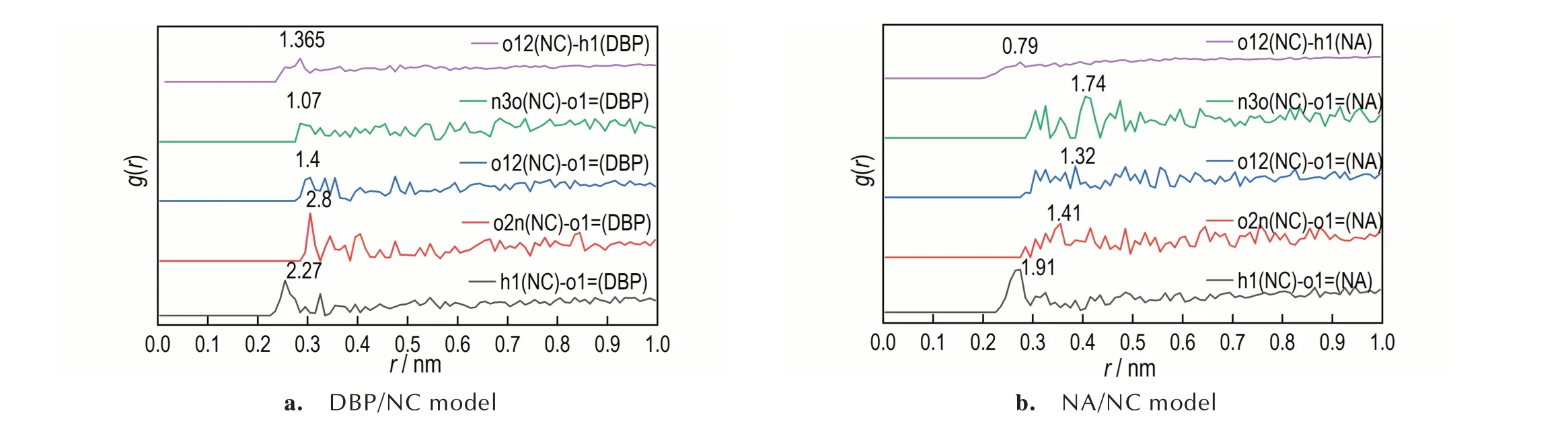
图7 DBP/NC、NA/NC 模型的径向分布函数Fig.7 Radial distribution functions of DBP/NC and NA/NC model

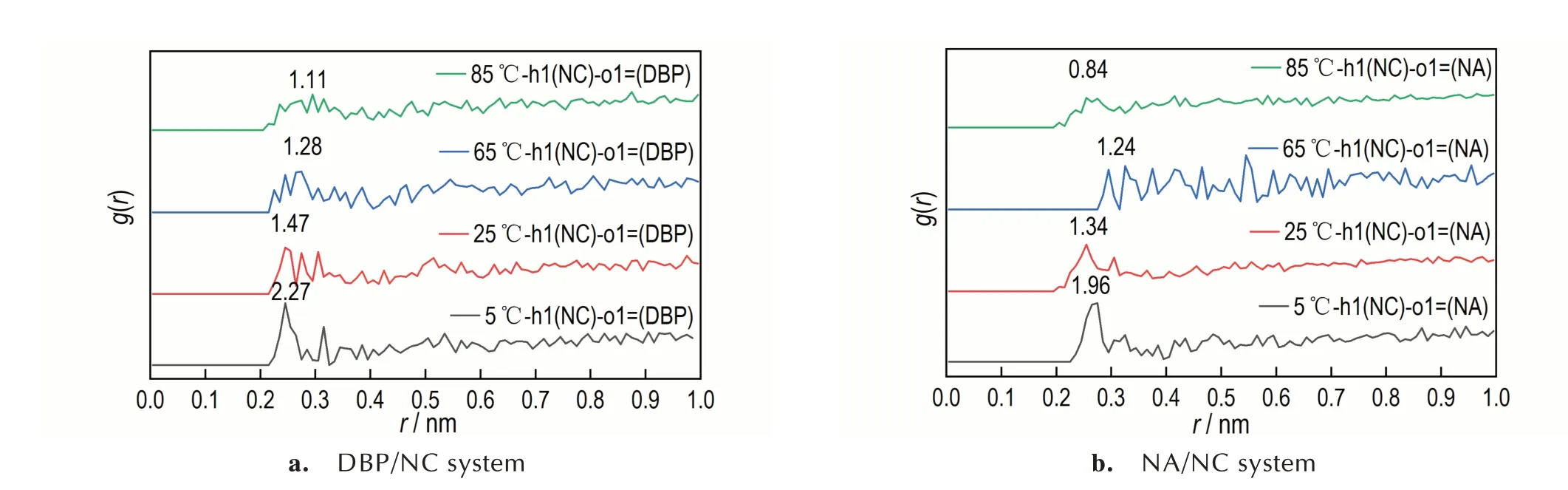
图8 DBP/NC、NA/NC 体系在不同温度下的径向分布函数Fig.8 Radial distribution functions of DBP/NC and NA/NC model at different temperatures

3.2.2 DBP、NA 在双基发射药体系中的径向分布函数

由于篇幅有限，因此仅选取形成氢键作用力最大的NC（h1、o12）与DBP（o1=）、NA（o1=）、NG（h1）原子对进行径向分布函数分析，进一步探究DBP、NA 在不同NG 含量的双基发射药体系扩散能力不同的原因。由 图9 可 见，h1（NC）-o1=（NA）、h（NC）-o1=（DBP）的峰值g（r）均随着体系中的NG 含量增加而减小，这 是 由 于NG 的h1 原 子 与NC 的-ONO2基 团 的o12 原 子 形 成 氢 键，使 得NC 与DBP、NA 之 间 的 作 用力相对微弱很多。如图10 所示，不同NG 含量的双基发射药体系的h1（NG）-o12（NC）的峰值g（r）均随着NG 的含量增多而增强。由此推测，增塑剂NG 的添加减弱了NC 与DBP、NA 之间的作用力，因此DBP、NA的运动更活跃，扩散能力增强。

3.3 自由体积分数

通过分子动力学模拟分析，分别得到了5，25 ℃和65 ℃下DBP/NC、NA/NC 的自由体积分布，结果如图11 所示。

Voccupied（Vo）是NC 和钝感剂DBP、NA 共同所占的体积，Vfree（Vf）表示分子间的间隙，即自由体积。如图11 所示，NC/DBP 的Vf均大于相同温度下的NA/NC。此外，DBP/NC、NA/NC 的Vf值均随温度的升高而显著增加，而Vo值均随温度的升高而略有减小。

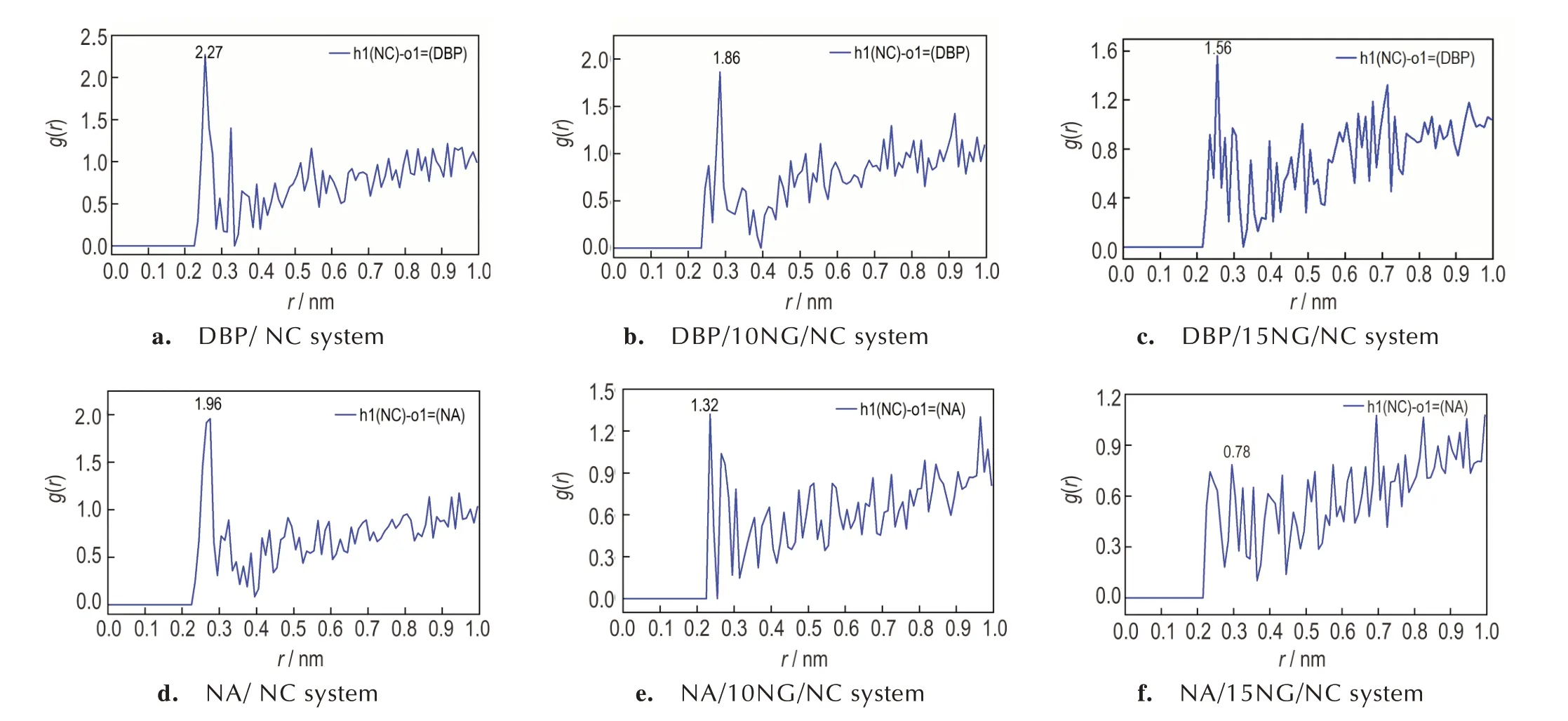
图9 DBP、NA 在双基发射药体系的径向分布函数Fig.9 Radial distribution functions of DBP and NA in double base propellant

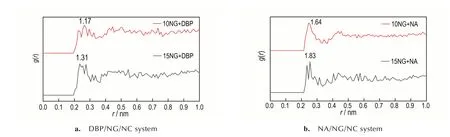
图10 NG（h1）与NC（o12）在不同体系中的径向分布函数Fig.10 Radial distribution functions of NG（h1）and NC（o12）in different systems

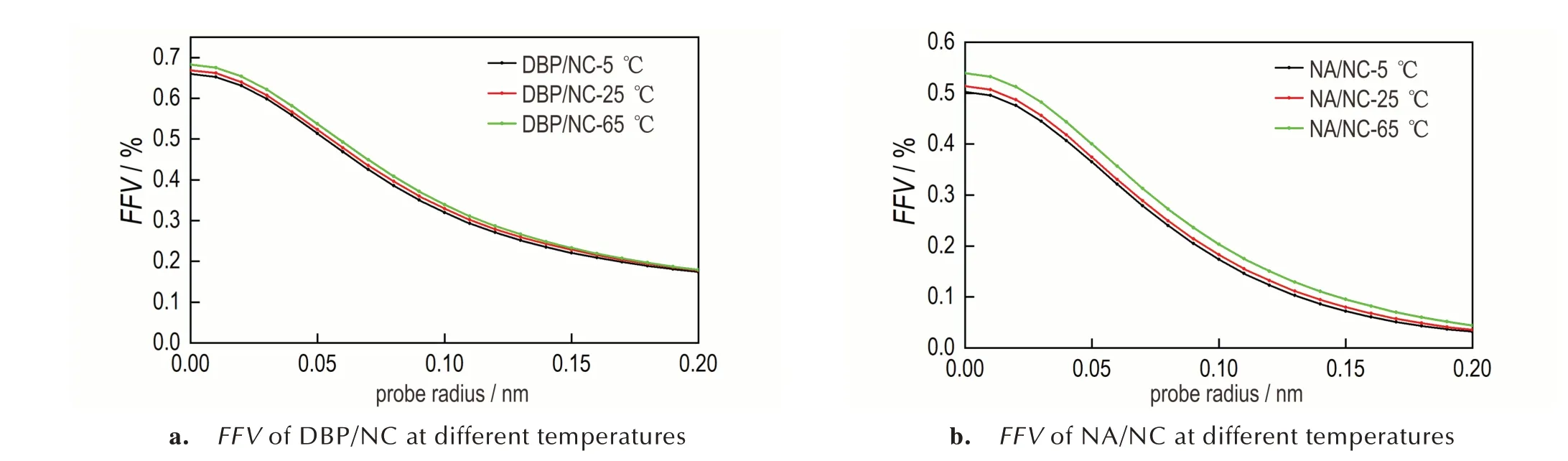
图12 DBP/NA 、NA/NC 在不同温度下的自由体积分数Fig.12 Fractional free volume of DBP/NA and NA/NC at different temperatures

体系的自由体积分数越大，提供给钝感剂运动的有效活动空间就越大，扩散也就越容易发生。由图12可以看出，相同温度下，体系内自由体积分数的大小顺序为DBP/NC＞NA/NC，可见DBP 的相对运动空间比NA 的大，这与扩散系数的顺序在逻辑上是一致的；此外，随着温度升高，DBP/NC、NA/NC 体系的自由体积分数也在增大，意味着分子的有效活动空间随着温度的升高而增大，这是由于高温使NC 的活动性增强、分子间距离增加，从而增加了体系的自由体积分数，这给DBP、NA 提供了更大的活动空间，这使DBP、NA 更易发生扩散。

4 结论

对DBP、NA 在NC 体系中扩散进行了分子动力学研究。研究结果表明：

（1）在相同温度下，钝感剂在发射药中的扩散系数大小顺序为：DBP＞NA，这说明NA 具有较强的抗迁移能力；此外，在25 ℃下，DBP与NA 的扩散系数分别为1.13×10-11m2·s-1和5.13×10-12m2·s-1，但在高温85 ℃下，DBP 与NA 的扩散系数分别为3.42×10-11m2·s-1和1.11×10-11m2·s-1，因此NA 相较于DBP 具有的抗迁移特性在高温时更为凸显。

（2）从NC 与DBP、NA 的分子间相互作用、体系的自由体积分数2 个方面分析了钝感剂扩散性能的微观机理。从微观角度解释扩散系数随着温度的升高而增大的原因为：高温导致NC 与DBP、NA 的分子间作用力减弱，DBP、NA 的运动变得更加活跃，同时体系的自由体积分数也在增大，增大了分子运动的有效活动空间，这均是DBP、NA 扩散能力增强的原因。

（3）在25 ℃下，DBP、NA 的扩散系数均随着NG含量的增加而增加，当双基发射药体系中NG 含量分别 为0%、10%、15%，DBP 的 扩 散 系 数 分 别 为7.03×10-12，8.05×10-12，1.41×10-11m2·s-1；NA 的扩散系数分别为4.05×10-12，6.96×10-12，9.33×10-12m2·s-1。这是由于NG 含量的增加使得NC 与DBP、NA 之间的分子作用力均减小，DBP、NA 的运动变得更加活跃，扩散能力增强。