典型车-桥系统气动力的雷诺数效应
2021-02-03何旭辉邹云峰
张 兵,何旭辉,周 佳,邹云峰
(1.中南大学 土木工程学院, 湖南 长沙 410075;2.高速铁路建造技术国家工程实验室, 湖南 长沙 410075)
随着高速铁路的迅速发展,列车车体轻量化和行驶高速化使得风荷载作用下的行车安全问题变得愈加突出[1-2]。既有高速列车愈加流线的外形可能会使列车气动力的雷诺数效应进一步加剧,同时列车的存在会使得桥梁对雷诺数的敏感性发生变化,为精确测量桥梁和列车受到的气动力,有必要对车-桥组合系统的雷诺数效应进行研究。
目前对于桥梁气动特性雷诺数效应的研究主要集中于桥梁单体[3-7],对于侧风下的高速列车气动特性国内外学者采用现场实测[8-9]、数值模拟[10]和风洞试验[11-12]等方法进行了大量的研究,但对车-桥组合系统的雷诺数效应的研究非常少[13-15]。李永乐等[13-14]利用交叉滑槽系统对车桥系统的气动特性进行了多工况对比研究,得出雷诺数对车桥系统的气动特性影响较小;测试了车桥组合状态下车辆沿不同类型的桥梁运行时的气动特性,得出横向风作用下,雷诺数效应对车-桥组合状态中CRH2客车的气动特性有一定的影响。郭文华等[15]以高速列车与双线简支箱梁桥为原型,测试高速列车的头车、中车及尾车各自的气动力,雷诺数效应对桥上高速列车气动力系数的影响有限,其规律不明显。由于风洞尺寸和风速的限制,学者均采用较低的风速和较小的缩尺比模型,在低雷诺数范围内进行研究,得出车-桥系统的气动力受雷诺数影响较小。因此有必要在大雷诺数范围内对车-桥系统气动力的雷诺数效应进行系统的研究,以完善和总结车-桥系统气动力的变化规律。
本文在满足风洞断面阻塞率的情况下选择最大比例车桥模型,在风洞和模型允许范围内最大程度的增加风速(中南大学风洞实验室高速段风速范围0~94 m/s),在相对较大雷诺数范围内研究车桥气动力随雷诺数的变化规律,即使不能达到实际车桥雷诺数,但是也能够反映雷诺数效应对不同的气动力的影响趋势,从一定程度上拓宽以往试验的雷诺数效应曲线。
1 节段模型风洞试验
试验桥梁模型采用32 m典型高速铁桥路梁模型,试验列车采用CRH2型经典高速动车组,模型采用1∶25的几何缩尺比。桥梁节段模型长为1.5 m,高为0.141 2 m,宽为0.492 2 m,试验列车分为头车、中车、尾车三部分,已有研究表明[16],列车在静止时,头车和尾车的阻力均远大于中车;列车处于运动状态时,头尾车的气动力变化非常明显。因此本文主要针对列车的头尾车进行研究,由于头车与尾车的外形相同,并考虑桥梁节段长度的限制,试验共制作了整列头车、整列中车、车头部分和中车部分四个节段作为简化列车形式。
风洞试验在中南大学高速实验段均匀流场条件下进行,采用测压形式进行车桥气动力测试,采样频率为312.5 Hz,采样时间为30 s,桥梁和列车测试模型及测压孔布置方式分别见图1和图2。桥梁节段模型取4个断面布置测压孔,分别为0.13、0.43、0.57、0.87L处,每个断面布置43个测点;列车头车模型布置13个风压测点断面,车头部分布置9个,车身部分布置4个,测点布置方式见图2。
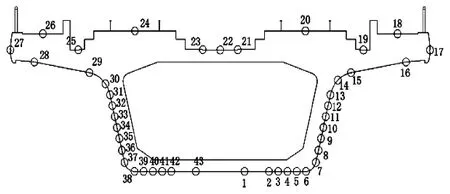
图1 高速铁路典型简支梁断面测点布置
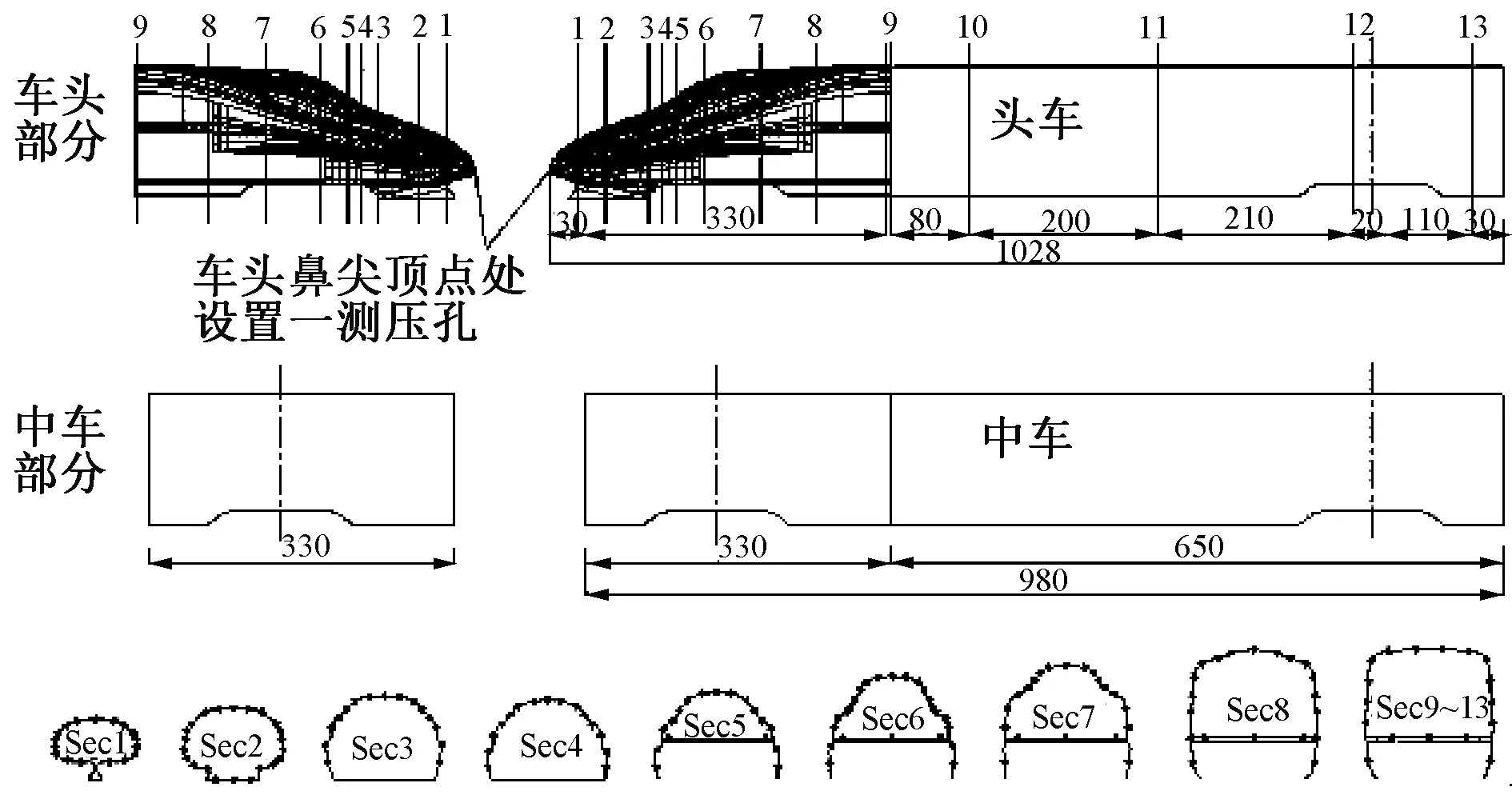
图2 CRH2高速列车断面模型及测点布置(单位:mm)
试验研究了简支梁单桥、列车和典型车 桥组合在均匀流作用下气动力特性的雷诺数效应。车桥组合工况见表1,典型车桥组合试验模型见图3。
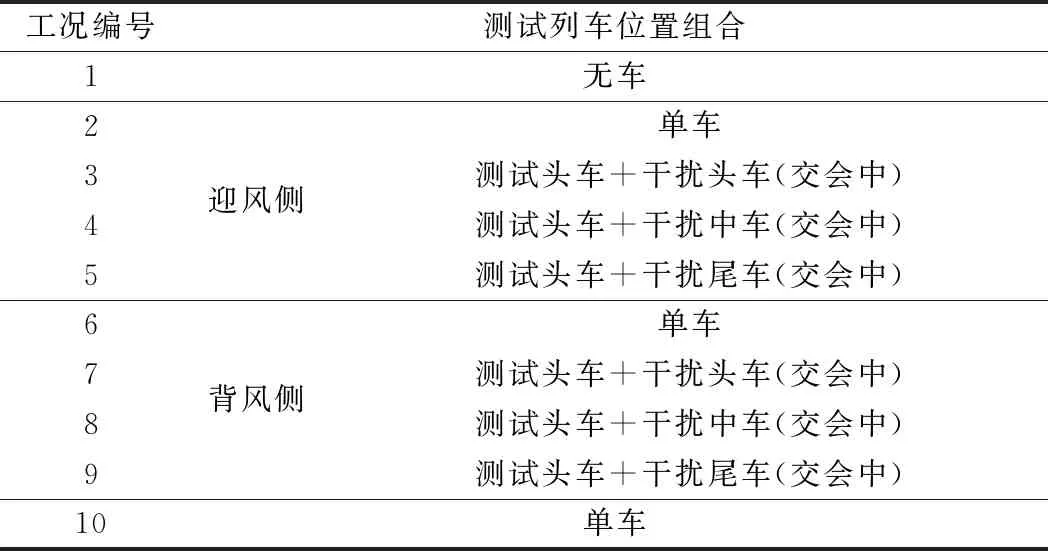
表1 车桥组合工况表

图3 工况4试验
2 数据处理
利用同步测压技术对桥梁和列车进行测压可以得到桥梁和列车表面的压力分布,每一点的风压可以用压力系数CPi进行描述,其定义为
(1)
式中:Pi为试验测点处测得的风压,以指向试验模型表面的压力为正;P∞为无穷远处试验参考高度处的静压;U∞为参考高度无穷远处的来流风速,风洞试验中取试验风速;ρ为空气密度,通常取1.225 kg/m3。
列车头车表面风压系数是某一点的受力情况,而列车头车的整体受力特性用三分力系数进行描述,其定义为
(2)
(3)
(4)
式中:CD、CL、CM分别为阻力系数、升力系数、力矩系数,其中列车的力矩系数为倾覆力矩系数,桥梁的力矩系数为扭转力矩系数;H、B、L分别为阶段模型的高度、宽度和长度;FS、FL、M分别为阻力、升力和力矩;U为来流风速。在此次试验中通过对各断面测压点的积分得到列车和桥梁的气动力,其计算公式为
(5)
(6)
(7)
式中:Pi(t)为测点风压时程;FS(t)、FL(t)、M(t)分别为体轴坐标下模型所受到的阻力、升力和力矩时程;Li为第i点对应的积分尺度;αi为第i点内法线与水平线的夹角;Xi和Yi为第i测点与模型倾覆点或扭转中心的横向距离和垂直距离。
3 试验结果分析
3.1 典型单桥状态
典型单桥状态工况试验风速5~30 m/s(其中8~30 m/s,梯度为2 m/s),桥梁模型特征长度(即高度)为0.141 2 m,在雷诺数Re=4.71×104~2.82×105的范围内测量了典型高速铁路简支梁模型的表面风压时程,总结其变化规律。攻角为-6°、-4°、-2°、0、2°、4°、6°时桥梁的气动力系数随雷诺数Re的变化规律,见图4。

图4 雷诺数对桥梁气动力系数的影响
由图4可知,当攻角为-2°~6°时,桥梁力系数受雷诺数Re的影响较小,阻力系数基本为定值在1.2左右,且随雷诺数存在微小的降低趋势;升力系数在0.4~0.6之间波动;力矩系数较小,基本为定值0.08,且随雷诺数增大存在微弱的上升趋势。而随着负攻角的增大(-4°~-6°),气动力系数分别在Re=2.26×105和Re=1.51×105处突然降低,降低幅度达到25%,这是由于随着负攻角的增大,桥梁上表面的迎风面积增加,风流过桥梁断面上表面没有明显的桥面流动分离点,在一定程度上削弱了桥梁断面的钝体程度,降低了其气动力系数。图4中曲线从某种程度上说明了桥梁在攻角较小或者正攻角状态下,流动分离点固定于桥梁上下表面的边缘上,基本不受雷诺数Re的影响,而负攻角的增加一部分减小了流体的分离,对流动的阻碍能力降低,从而降低了气动阻力,也不难理解气动升力的降低,作为阻力与升力共同效应的扭矩也在降低。
3.2 单列车状态
试验风速5~50 m/s(梯度为5 m/s),列车模型特征长度(即高度)为0.14 m,在雷诺数Re=4.67×104~4.67×105的范围内测量了列车模型的表面风压时程,总结其变化规律。
雷诺数对列车车头和车身断面气动力的影响见图5,由图5可知,由于车头的外形复杂且流线性较大,具有明显的三维绕流效应,其阻力系数明显小于车身二维钝体断面的数值。单车受雷诺数变化较为敏感,雷诺数Re<1.5×105时随雷诺数的增加,列车的阻力降低,升力在升高,且车身的改变程度高于车头;1.5×105

图5 雷诺数对列车气动力系数的影响
3.3 典型车桥组合状态
试验采用风速5~30 m/s的范围(其中8~30 m/s,梯度为2 m/s),此时桥梁雷诺数Re范围为4.71×104~2.82×105,列车雷诺数Re范围为4.67×104~2.80×105,并在此范围内研究典型车桥组合条件下的雷诺数效应。车桥经典组合工况3(迎风测试头车与干扰中车交会中)在不同攻角下列车车头、车身、桥梁气动力随雷诺数的变化规律,见图6。
由图6可知,车头和车身的阻力系数均随雷诺数的增加而降低,升力系数随雷诺数增加而升高,且车头的变化幅度相对缓慢,明显低于车身的变化幅度,阻力与升力均在攻角由负转正的过程中降低,这主要是因为随着攻角向正方向转动的过程中,桥梁迎风面积相应在减小,来流正压相对减小,即减小了迎风面与背风面的压力差值,降低了阻力。倾覆力矩为阻力与升力共同作用的结果,其随雷诺数的增加而降低,这也同时说明了力矩的贡献成分中阻力占了绝大部分。
与列车不同的是,桥梁的阻力与升力系数随攻角的增大而升高,且与单桥状态明显不同的是,桥梁由于列车的干扰对雷诺数变得非常敏感,能看到其阻力与升力在雷诺数Re<1.5×105时随雷诺数的增加而显著降低,最大降幅达到45%左右,当Re>1.5×105后基本稳定,不随雷诺数发生变化。这主要是由于列车的干扰改变了桥梁上部的外形,流线的列车,由尖锐棱角的钝体转化到具有弧形表面的钝体,使得表面边界层从层流变为紊流状态,来流分离点向下游移动,尾流区域变窄,进入雷诺数的临界区域,阻力系数发生骤降。扭转力矩与阻力升力的变化规律相同。
3.4 车桥组合类型的影响
由于列车与桥梁在不同攻角下随雷诺数的变化规律一致,故取某一攻角下的不同车桥组合状态下车桥气动力进行分析。由图7可知,迎风侧车头、车身的气动力系数对雷诺数的敏感程度明显高于背风侧工况,伴随着背风侧干扰列车与迎风侧测试列车交会的过程(工况3~工况5),气动力系数也随着雷诺数的变化程度增加,而背风侧测试列车的气动力较为稳定,基本不随雷诺数改变。
桥梁在典型车桥组合下气动力随雷诺数的变化规律见图7。由图7可知,桥梁在单体存在时,其各气动力系数基本不随雷诺数发生改变,当桥梁上有列车干扰时,在Re<1.5×105时阻力系数随雷诺数的增加而显著降低,之后趋于稳定,升力系数较之阻力系数变化幅度较小。各车桥组合工况下桥梁的气动力随雷诺数的变化规律基本一致,且有车干扰时的桥梁气动力明显低于单桥存在时的数值。
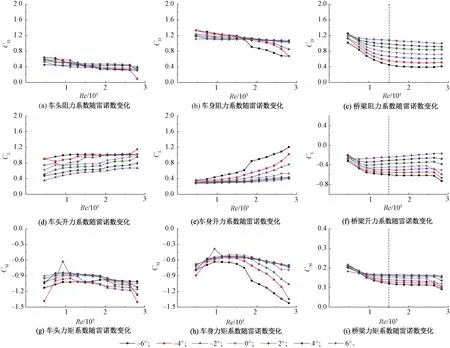
图6 不同攻角下雷诺数对列车和桥梁气动力的影响
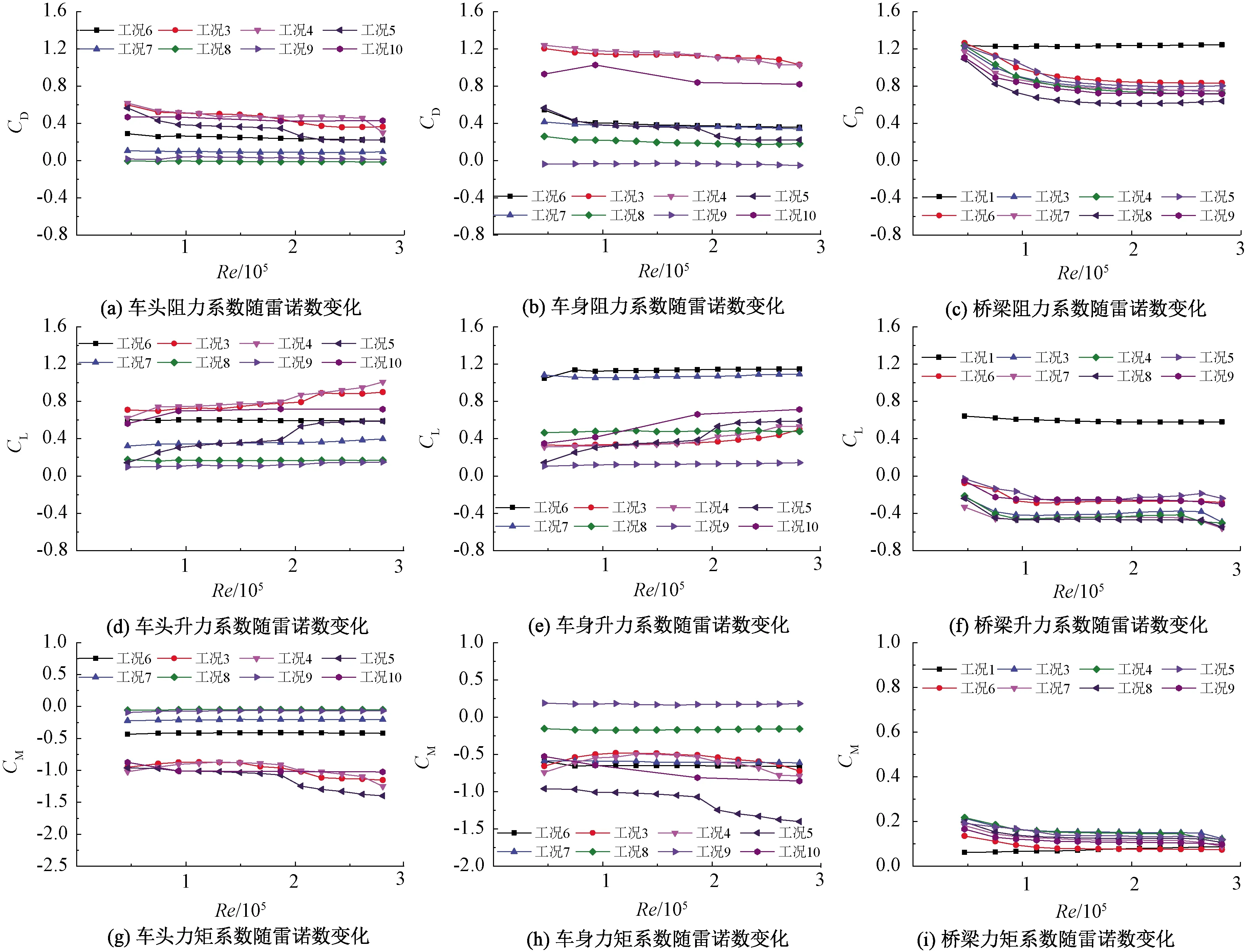
图7 不同典型车桥组合状态下雷诺数对列车和桥梁气动力系数的影响
4 结论
本文主要讨论了均匀流作用下简支梁单桥、列车和典型车桥组合气动力的雷诺数效应,分析了雷诺数对车桥气动力的影响,并总结变化规律,得到以下结论:
(1)简支梁单桥在试验雷诺数范围内的影响较小,仅个别攻角下阻力降低。
(2)对典型车桥组合工况(工况3)进行气动力分析,发现列车与桥梁气动力在不同风攻角下随雷诺数变化一致。列车在试验雷诺数范围内阻力均随雷诺数的增加而降低,升力增大;桥梁在Re<1.5×105时阻力降低显著,最大降幅达45%,说明了桥梁由于列车的干扰存在对雷诺数变得十分敏感。
(3)对迎风侧与背风侧测试列车与干扰列车交会的各工况进行分析,迎风侧列车的气动力对雷诺数的敏感程度高于背风侧工况,迎风侧列车气动力随雷诺数的增加而降低,背风侧基本没有变化。
