不同矫正位置对落叶松分位数削度方程预测精度的影响

辛士冬，何 培，姜立春

(东北林业大学林学院，森林生态系统可持续经营教育部重点实验室，黑龙江 哈尔滨 150040)

削度方程可以描绘树干轮廓，预测树干任意高度处的直径，预测树干任意区间的材积以及商品材积，也是森林经营管理和规划、林分生长与收获的重要工具[1-3]。曾伟生等[4]指出未来材种出材率表的编制将采用削度方程来进行。

树干形状的变化可能会受立地质量、林分密度、竞争和间伐等多种因素的影响。由于每一株树木的干形都不同，在削度方程中引入树干上部直径进行矫正，考虑单木之间以及林分之间的变异情况，这种矫正方式约束削度方程必须通过已知的树干上部直径位置，使削度方程的预测精度得到提高[5-6]。Czaplewski等[7]使用树干上部直径对Max-Burkhart分段削度方程进行矫正，与未矫正的模型相比，其均方根误差(RMSE)降低了10%～25%。Cao[8]研究发现利用胸高以上50%高度处的直径矫正模型最为合理。Kozak[9]利用可变指数模型提出了使用树干上部直径矫正的最佳高度区间为胸高以上40%～50%的高度；然而，Gómez-García等[10]使用Kozak的可变指数削度方程发现利用树干8 m高度处直径提供的矫正可以使模型的RMSE从1.55 cm降低到1.34 cm。Sharma等[11]基于黑云杉(Piceamariana)和北美短叶松(Pinusmariana)提出以树干总高度的34%～38%测量的树干上部直径进行矫正最好。

分位数回归方法被提出以来，已经被广泛使用于描述响应变量与解释变量的关系[12]。分位数回归估计可以量化响应变量的整个条件分布，并对响应变量不同分位数点的协变量效应进行评估，从而为分析数据提供了更丰富的信息[13]。落叶松(Larixgmelinii)是中国东北、内蒙古林区的主要树种，分布于温带及寒温带，是东北地区主要三大针叶用材林树种之一，所以对天然落叶松干形精准预测的研究具有重要意义[14]。而目前利用分位数回归以及系统研究不同矫正位置对树木干形的影响还鲜见报道，鉴于此，本研究利用非线性分位数方法建立落叶松分段削度方程，并以树干相对高20%、30%、40%、50%、60%、70%处及胸径到树尖的中间位置(50%*)的直径对削度方程进行矫正，分析使用不同矫正位置对削度方程预测精度的影响，为落叶松天然林干形的精准预测提供理论依据。

1 材料与方法

1.1 研究区概况

研究地点位于大兴安岭松岭林业局壮志林场(123°29′～125°11′E，50°9′～51°23′N)，其整个自然实体由伊勒呼里山绵延南伸的两条低山丘陵组成，西北高、东南低。海拔为400～700 m。地处寒温带，属大陆性气候。最高气温35.5 ℃，最低气温-43.8 ℃，年平均气温-3 ℃。年降雨量415～500 mm，多集中在7、8月，占全年降水量的48.9%，年无霜期为100～110 d，植物生长期为90～100 d，森林植被由东南向西北明显过渡。该林场主要树种包括兴安落叶松、白桦(Betulaplatyphylla)、樟子松(Pinussylvestrisvar.mongholica)、山杨(Populusdavidiana)等。

1.2 样本数据的采集

本研究所用的数据来源于该林场不同林分的落叶松天然林样地，树木被伐后，测量胸径、树高及树干相对高(0、2%、4%、6%、8%、10%、15%、20%、30%、40%、50%、60%、70%、80%、90%)15个位置的直径。样地采集样本214株，剔除2株明显异常的数据，用于建模的样本数量为159株，用于检验的样本数量53株，共计212株，将其以75%和25%随机分成建模数据和独立检验数据，落叶松各样本统计量见表1。

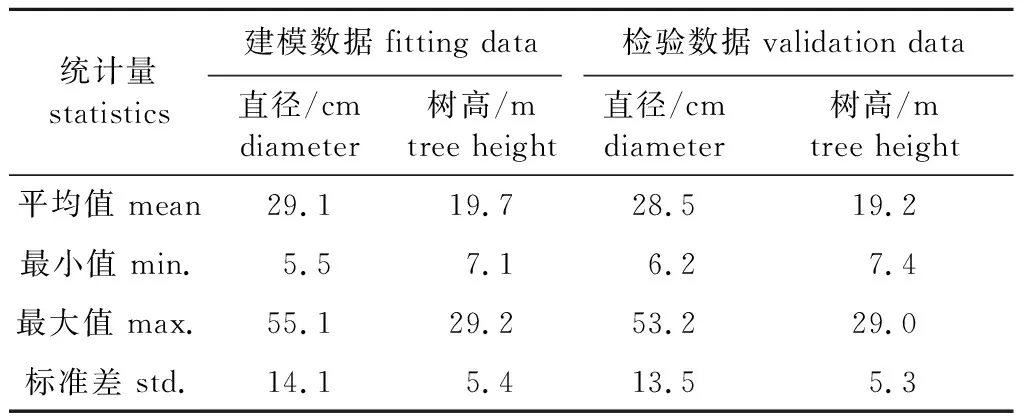
表1 落叶松天然林各样木调查因子统计量

1.3 基础削度方程

目前，削度方程在国内外成功应用主要为可变指数和分段削度方程[15-19]。分段削度方程不仅可以灵活地适应树干复杂的几何变化形状，还可以直接积分计算材积和商品材积，这也是分段削度方程在应用时优于可变指数削度方程的主要方面[20]。因此本研究采用Max and Burkhart分段削度方程作为基础模型[20]，此方程由3个不同的二次函数和2个连接点组成，能够适应树干上部、中部、下部的几何形状，其相应的几何体为锥体、抛物线体、凹曲线体，对方程进行直接积分可以得到材积方程[21]。具体方程形式如下：

y=a1(x-1)+a2(x2-1)+a3(b1-x)2I1+

a4(b2-x)2I2+ε。

(1)

式中：y=d2/D2，d为树干高h处的直径，D为胸径；x=h/H，H为全树高，h为从地面到所需位置的高度；当x≤b1时，I1=1；当x>b1时，I1=0; 当x≤b2时,I2=1；当x>b2时，I2=0；a1、a2、a3、a4为待定参数；b1、b2为树干下部和上部拐点处的相对高度；ε为模型的误差项。

1.4 分位数回归模型

分位数回归是一种估计因变量完整的条件分布和评估不同分位数预测变量影响的方法，把模型(1)表示成分位数削度方程如下：

yτ=a1τ(x-1)+a2τ(x2-1)+a3τ(b1τ-x)2I1+

a4τ(b2τ-x)2I2+ετ。

(2)

分位数回归的优势在于可以提供任意分位点处解释变量的变化趋势，包括数据的上下边界，误差的分布也不需要任何的假设，并且不受数据中异方差的影响，是一种稳健的回归建模和推断方式[22-24]。分位数回归的参数估计具体是使损失函数Lmin完成最小值的线性规划得以实现：

(3)

式中：τ=0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，具体采用SAS软件的 PROC NLP模块进行拟合[25]。

1.5 模型检验

(4)

1.6 模型评价指标

模型的评价采用平均误差[MAB，式中记为σ(MAB)]、相对误差[MPB，式中记为σ(MPB)]来对比不同矫正位置及不同检验方式模型的预测精度。它们相应的数学表达式为：

2 结果与分析

2.1 基本模型与分位数模型的参数估计

基本模型利用SAS软件中的PROC MODEL过程进行参数估计，由于落叶松干形数据存在空间相关性，不满足模型的基本假设条件，所以在参数估计过程中添加连续一阶自回归函数CAR(1)来消除干形数据的自相关性[27]。分位数回归选取9个不同的分位点(τ=0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9)，采用SAS软件中的PROC NLP过程进行参数估计，结果见表2。可以看出，不同分位数模型的参数估计值都有所波动，并且Max等[21]分段削度方程在9个分位点下都可以得到参数估计，说明分位数回归方法的灵活性较强，可以提供不同分位点下树干曲线的变化趋势，为干形数据分析提供了更丰富的信息。

表2 落叶松削度方程的参数估计值

2.2 落叶松树干曲线模拟

为了避免分位数曲线出现不能描述树干曲线的异常情况，本次试验利用拟合数据和表2的参数估计值，并以基本模型、中位数模型、基于3个分位数组合(τ=0.1、0.5、0.9)、5个分位数组合(τ=0.1、0.3、0.5、0.7、0.9)、7个分位数组合(τ=0.1、0.2、0.3、0.5、0.7、0.8、0.9)和9个分位数组合(τ=0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9)为例，模拟了落叶松的分段削度方程在不同分位点的树干曲线(图1)。基本模型(图1A)和中位数(τ=0.5)模型(图1B)只提供了数据中心位置的变化趋势。

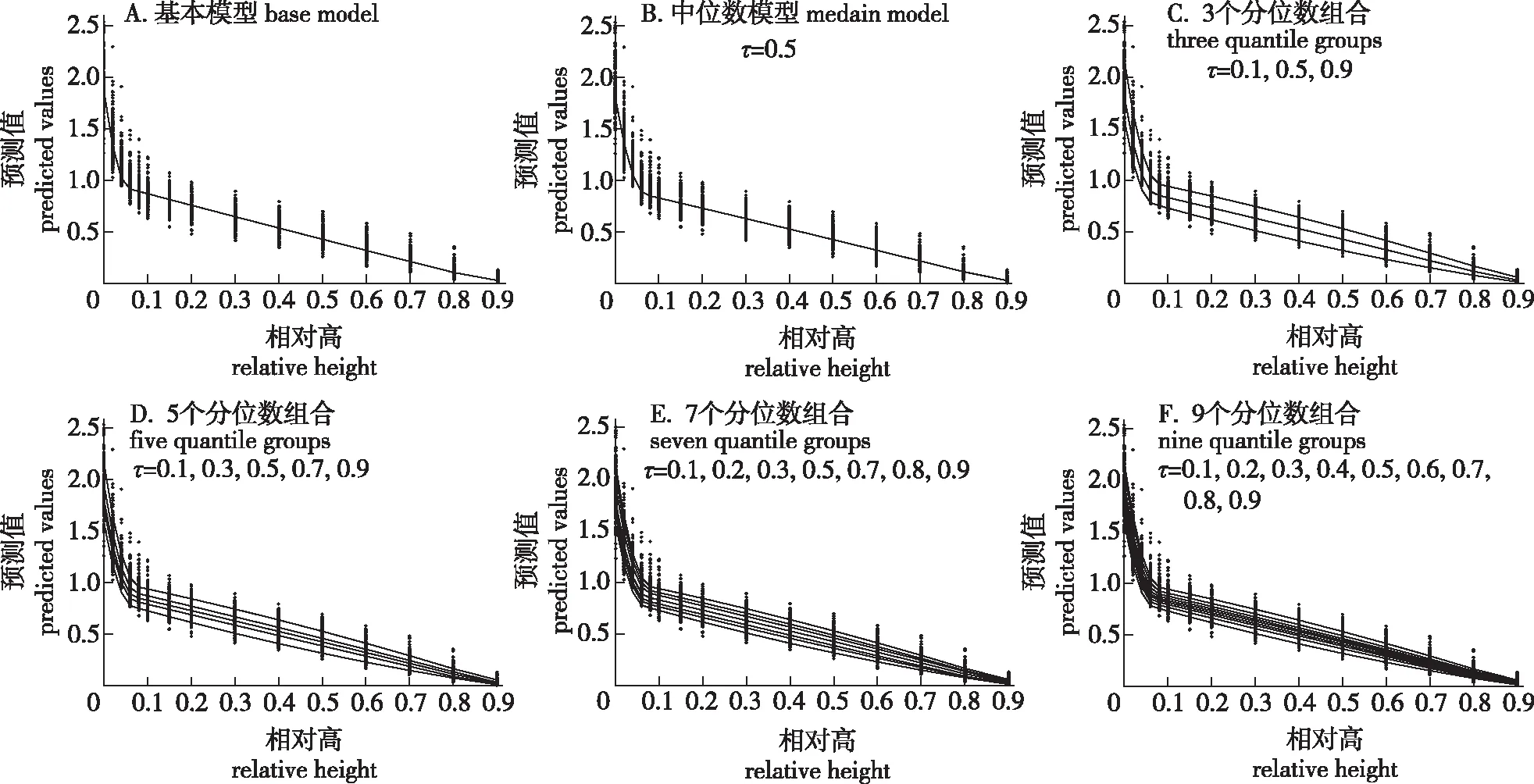
图1 落叶松树干曲线模拟Fig.1 Stem taper curve simulation of Larix gmelinii

从图1也可以看出，随着分位点个数的增加，基于分位数回归的削度方程可以涵盖的数据范围更大，提供的信息也更加丰富。无论是在数据的中间还是数据的边缘，利用分位数回归的方法都可以进行模拟，体现了分位数回归方法较强的灵活性，可以更为全面地描述树干形状的变化趋势。

2.3 模型预测精度分析

2.3.1 传统预测检验

基于表2中各模型的参数估计值和53株落叶松独立检验样本(表1)，利用SAS软件计算基本模型及各分位数削度方程的平均误差(MAB)和相对误差(MPB)见表3。从表3可以发现，分位数(τ=0.5)模型的MAB和MPB略低于基本模型，更适合于预测落叶松树干曲线的变化趋势。

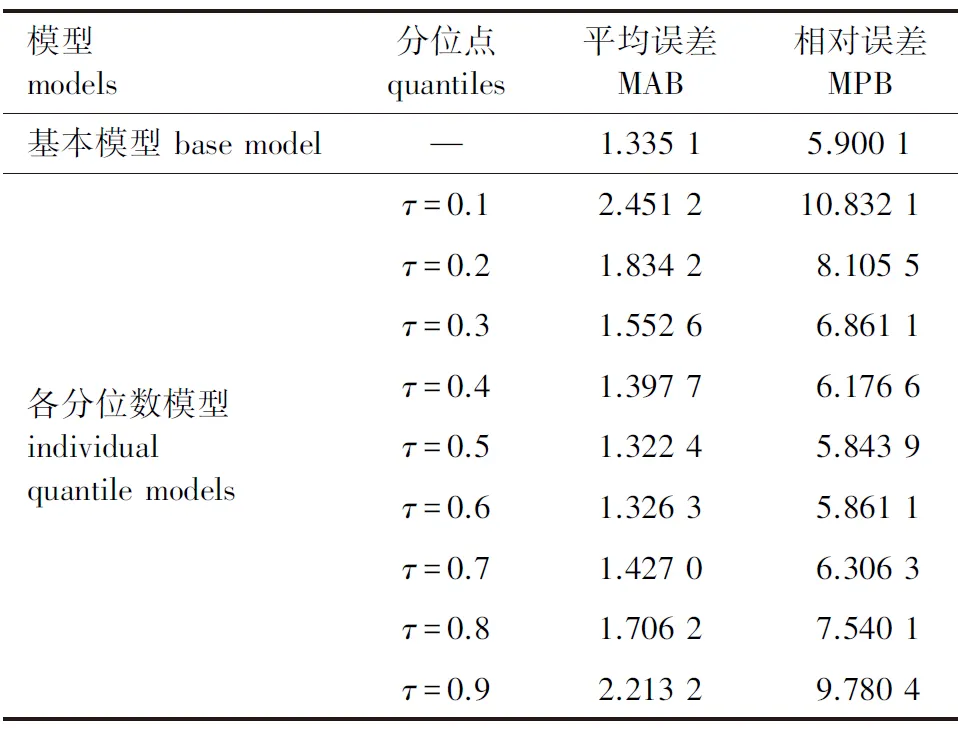
表3 落叶松削度方程的独立性检验

2.3.2 不同矫正位置对分位数组合模型预测精度的影响

使用不同矫正位置的分位数组合模型，采用Cao等[26]提出的检验方法进行检验，矫正位置的选取考虑了树干的形状变化规律，其高于胸径、低于树干最上部的拐点(即从抛物体转变为锥体的连接点)，所以本次试验选取树干相对高20%、30%、40%、50%、60%、70%的直径和胸径到树尖的中间位置(50%*)的直径对模型进行矫正。基于表2的参数估计值和公式(4)，采用SAS软件编写程序计算不同分位数组合模型及不同矫正位置的平均误差(MAB)和相对误差(MPB)，结果见表4。可以看出，利用相对高20%和70%处的直径进行矫正时，各分位数组合模型的平均误差和相对误差高于基本模型的统计量，说明矫正位置选取胸径和树干上部拐点附近不会提高模型的预测精度。使用树干相对高30%～60%处直径进行矫正的大多数分位数组合模型的统计量均优于未矫正的基本模型，而且使用树干不同高度的上部直径进行矫正时，最优的分位数组合模型并不一致，当使用相对高20%、30%、40%处的直径和胸径到树尖的中间位置(50%*)直径对分位数组合模型进行矫正时，其最优模型为3个分位数的组合模型(τ=0.3、0.5、0.7)，而当使用相对高50%、60%、70%的直径矫正时，其最优模型为5个分位数的组合模型(τ=0.3、0.4、0.5、0.6、0.7)。从表4也可以看出，并不是使用分位点越多的分位数组合模型预测精度越高，原因在于使用不同分位点的组合，树干上矫正位置高度h处的直径测量值位于不同的分位点之间，通过Cao等[26]提出的插值法生成不同的预测曲线，进而得到不同的预测值。本研究的最佳矫正位置为树干相对高40%处，其各分位数组合模型的MAB和MPB最低，最优模型为3个分数的组合模型(τ=0.3、0.5、0.7)，与未矫正的基本模型相比，MAB和MPB分别均下降13.5%。总体分位数组合模型的预测精度顺序为40% >50%*>50%>60%> 30%> 20%> 70%。

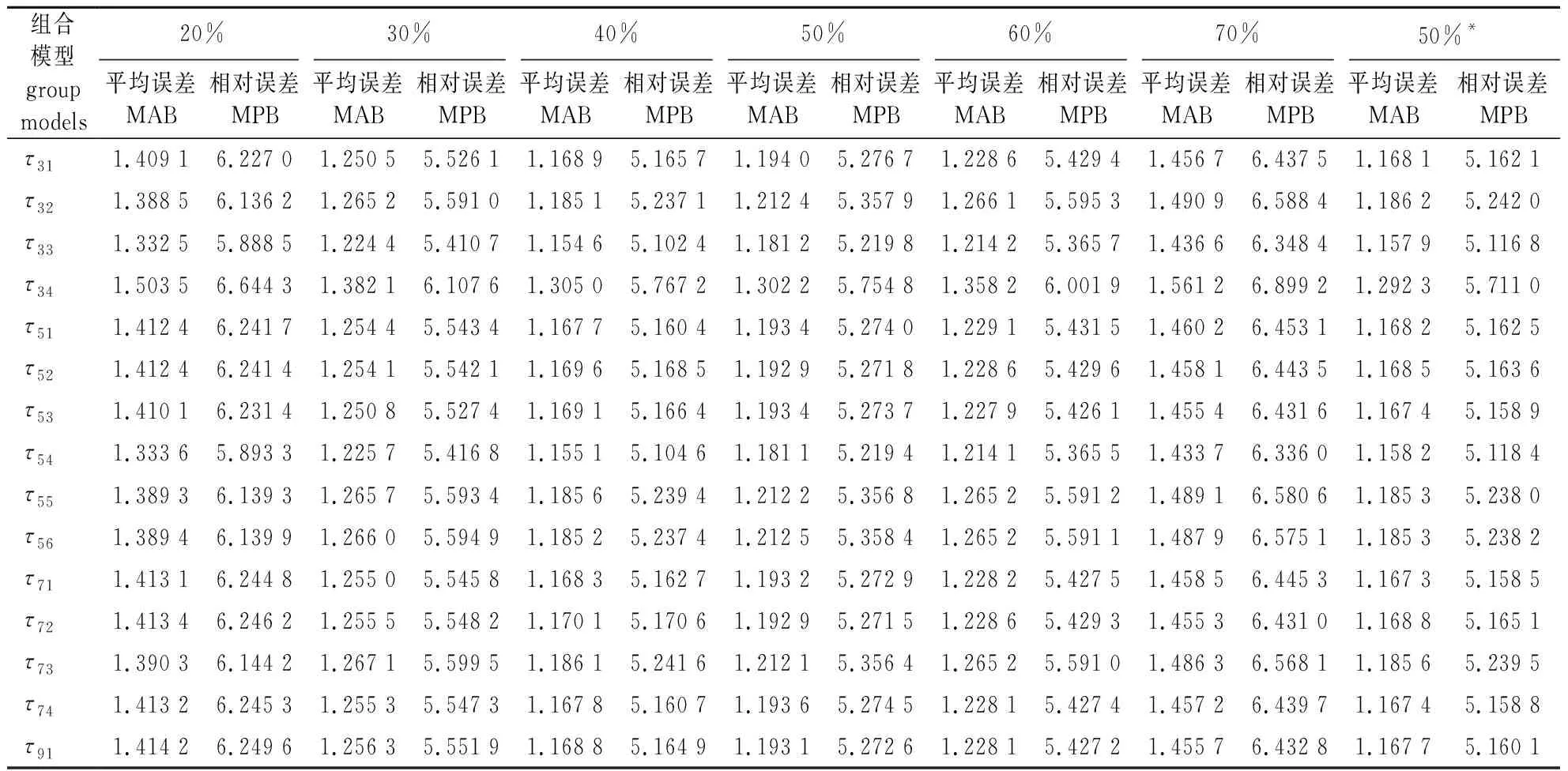
表4 基于不同矫正位置落叶松削度方程的统计量

3 讨 论

削度方程广泛应用于单木材积、林分蓄积的估算和森林碳汇的规划，具有重要的实际应用价值，其不仅是林分生长与收获模型的重要组成部分，也是森林经营管理中必不可少的手段，削度方程预测单木材积和林分材积是否精确直接决定了森林规划系统方案的科学性。本研究利用一个树干上部直径对分位数分段削度方程进行矫正，选取的矫正位置在高于胸径位置并低于树干上部拐点位置(即树干中间抛物体转变为树干顶部锥体的直径)。最低矫正位置的选择是由数据中最小树高决定的，本研究数据中胸径高度为1.3 m，最小树高为7.1 m，其胸径高度占总树高的18.3%。最高的矫正位置要低于树干上部拐点，主要由模型的参数估计值决定，基本模型的树干上部拐点参数为0.789 2，基于不同分位数的树干上部拐点参数范围为0.791 3～0.862 9，所以本研究矫正位置选取树干相对高度的20%～70%(以10%为间隔)。选取胸径到树尖的中间(50%*)处的树干上部直径作为矫正位置，是因为有研究者指出这一矫正位置为最佳矫正位置[26]。

从不同矫正位置的落叶松各分位数组合模型的统计指标可以发现，准确选择树干上部直径的矫正位置至关重要，不同的矫正位置对模型的精度影响较大。本研究的最佳矫正位置为树干相对高40%处，这与Cao等[26]研究美国路易斯安纳州的火炬松(P.taedaL.)所提出的最佳矫正位置并不一致，Cao等[26]提出5个分位数组合模型的预测精度最高，并且只研究对比了3个分位数组合(τ=0.1、0.5、0.9)和5个分位数组合(τ=0.1、0.3、0.5、0.7、0.9)模型。本次试验考虑了多种分位数组合，并构建了3、5、7、9个分位数的组合模型，但结果表明3个分位数组合模型(τ=0.3、0.5、0.7)的预测精度最高，该组合模型与未矫正的模型相比，MAB和MPB均下降13.5%，可以为该地区落叶松树干干形提供相对精准的预测。

4 结 论

1)基于中位数回归(τ=0.5)的削度模型预测精度略优于非线性回归的削度模型。

2)在削度模型中引入树干相对高40%处的直径并采用3个分位数的组合模型(τ=0.3、0.5、0.7)进行矫正，预测能力明显得以提高。

3)本研究选用Max and Burkhart削度方程，是因为该方程具有明显的几何生物学意义以及能直接积分计算各种材积[20]，当选用不同的削度方程进行矫正时，分位数组合以及矫正位置都可能发生变化。