现代有轨电车不同轨道的振动传递特性试验研究

张 迅 ，李 茜 ，郝晨曦 ，游颖川 ，陈伟杰 ，蒲 潏 ，徐煜进

（西南交通大学土木工程学院，四川 成都 610031）

随着城市化的快速发展，交通问题备受关注. 与其它交通方式相比，现代有轨电车具有环保好、运量大、造价相对较低等优势，故在我国各大城市中的应用越来越多. 为了缓解现代有轨电车引起的振动和噪声问题，当前多采用嵌入式轨道. 不同于常规离散支承的轨道结构形式，嵌入式轨道将钢轨连续嵌入弹性材料中，克服了轨道变形和受力不均匀的问题，且具有更好的动态轨道响应和阻尼特性[1-3].

国内外学者对嵌入式轨道在隔离钢轨振动和降低轨道辐射噪声方面开展了一定的研究. van Lier[4]通过对嵌入式轨道进行优化后，使得轮轨噪声相比有砟轨道降低了4～6 dB(A). Nilsson等[5]采用波导有限元-边界元法研究了嵌入式轨道的辐射噪声，重点研究了弹性材料的阻尼特性对钢轨振动的影响，分析得出600 Hz以上的声辐射水平明显降低. Michas[6]将嵌入式轨道与声屏障配合使用后，使得路旁噪声降低了16 dB(A). Zhao等[7]的仿真结果显示：嵌入式轨道槽内型式为“I”型时可以降低辐射噪声3 dB(A)；若进一步增大钢轨垫板的弹性模量，则可降低辐射噪声4 dB(A). 江小州等[8]针对声振优势频段，从轨道板长度和高度、承轨槽宽度、PVC （poly vinyl chlorid）管直径等几个参数进行了优化. 针对400～500 Hz和800～1 000 Hz两个峰值噪声频段，江小州等[9]对材料参数和降噪块形状进行了优化，最终使得辐射声功率级总值降低了1.7 dB(A). 为了控制造价，杜几平等[10]提出采用降噪块部分替换高分子阻尼填充材料，并通过优化分析确保了降噪效果不显著降低.

嵌入式轨道与列车的动力相互作用同样引起了研究者的关注. Ling等[11]建立了有轨电车-嵌入式轨道耦合动力学模型，通过与传统扣件式轨道相比，嵌入式轨道在降低轮轨相互作用力、轨道部件的变形和振动、轨道缺陷和损伤等方面具有优势. 冯青松等[12-13]对简支梁、连续梁桥上嵌入式轨道的纵向力进行了仿真分析，得出了轨道纵向阻力、垂向刚度和轨板相对位移限值. Ryjáček等[14]针对钢桥上铺设嵌入式轨道的情况，通过模型试验和数值仿真研究了桥-轨相互作用.

本文以嵌入式轨道为研究对象，对钢轨振动衰减率、轨道各部件的频响特性和插入损失等进行了分析. 首先采用锤击试验方法实测了钢轨振动衰减率. 再与同一条线路上的扣件式普通轨道在安装弹性包覆材料前、后的测试结果进行了对比，以获取嵌入式轨道的插入损失. 最后，将嵌入式轨道与现有文献中典型减振轨道的实测结果进行了对比. 本文的研究成果可为今后进一步开展嵌入式轨道的减振降噪优化设计提供参考.

1 试验原理

1.1 锤击试验

根据ISO 7 626-5标准[15]，锤击试验是对结构施加一个脉冲激励力，同时采集激励和响应信号. 一次锤击激励相当于一次“扫频”试验，可以用来分析结构的动力特性. 在锤击激励下，结构振动微分方程为

将实测锤击力作为系统输入，实测加速度响应作为系统输出，则频响函数（frequency response function，FRF）定义为加速度响应的傅里叶变换与锤击力的傅里叶变换之比. 为了降低系统误差，可以利用输出信号和输入信号的互功率谱与输入信号的自功率谱之比计算频响函数，即

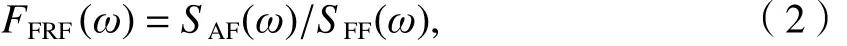
1.2 钢轨振动衰减率

钢轨振动衰减率（decay rate，DR）是量化钢轨振动沿纵向传递能力的重要指标[1,16]，单位为dB/m. 钢轨振动衰减率越小，钢轨受振动影响的长度就越大，从而导致钢轨辐射的噪声也越大. 当钢轨振动衰减率过低时（例如，小于0.1 dB/m），表示轨道系统的阻尼过小，钢轨有脱离扣件约束进行自由振动的趋势[1].

假设可将钢轨振动分解为横向和竖向两部分，且振动波幅值沿钢轨纵向按照指数衰减[17-19]. 基准点记为x0，则任意位置x处钢轨的频响函数幅值可表示为

钢轨辐射的振动能量与振动衰减率的关系为

理论上，可将钢轨振动衰减率视为频响函数幅值随着到基准点距离的增加而不断衰减的曲线. 然而，在实际操作中，钢轨振动响应被分解成竖向弯曲波和横向弯曲波，因此幅值的变化已不再是简单的指数衰减形式. 此时，采用离散点锤击测试的频响函数更符合实际情况，则式（5）可表示为

结合式（4）和式（6），可得钢轨振动衰减率为

2 试验方案

试验对象为某市现代有轨电车交通所采用的嵌入式轨道[20]（图 1）， 其中，59R2 型槽型钢轨被放置在轨道板承轨槽内，轨底设置橡胶弹性垫板，槽内填充浇筑料（高分子阻尼材料）形成弹性体，PVC管通过保持架和楔形块固定在钢轨两侧.

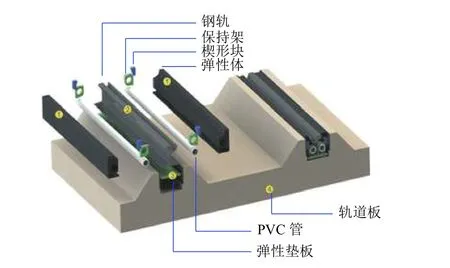
图1 嵌入式轨道示意Fig. 1 Schematic of embedded rail track

2.1 测点布置

由于在固定点进行锤击、不同位置处分别布置传感器进行测量的可操作性较低，因此根据动力互易定理，一般选择在固定点布置传感器，而在钢轨不同位置处进行锤击测试，测试方案如图2所示.

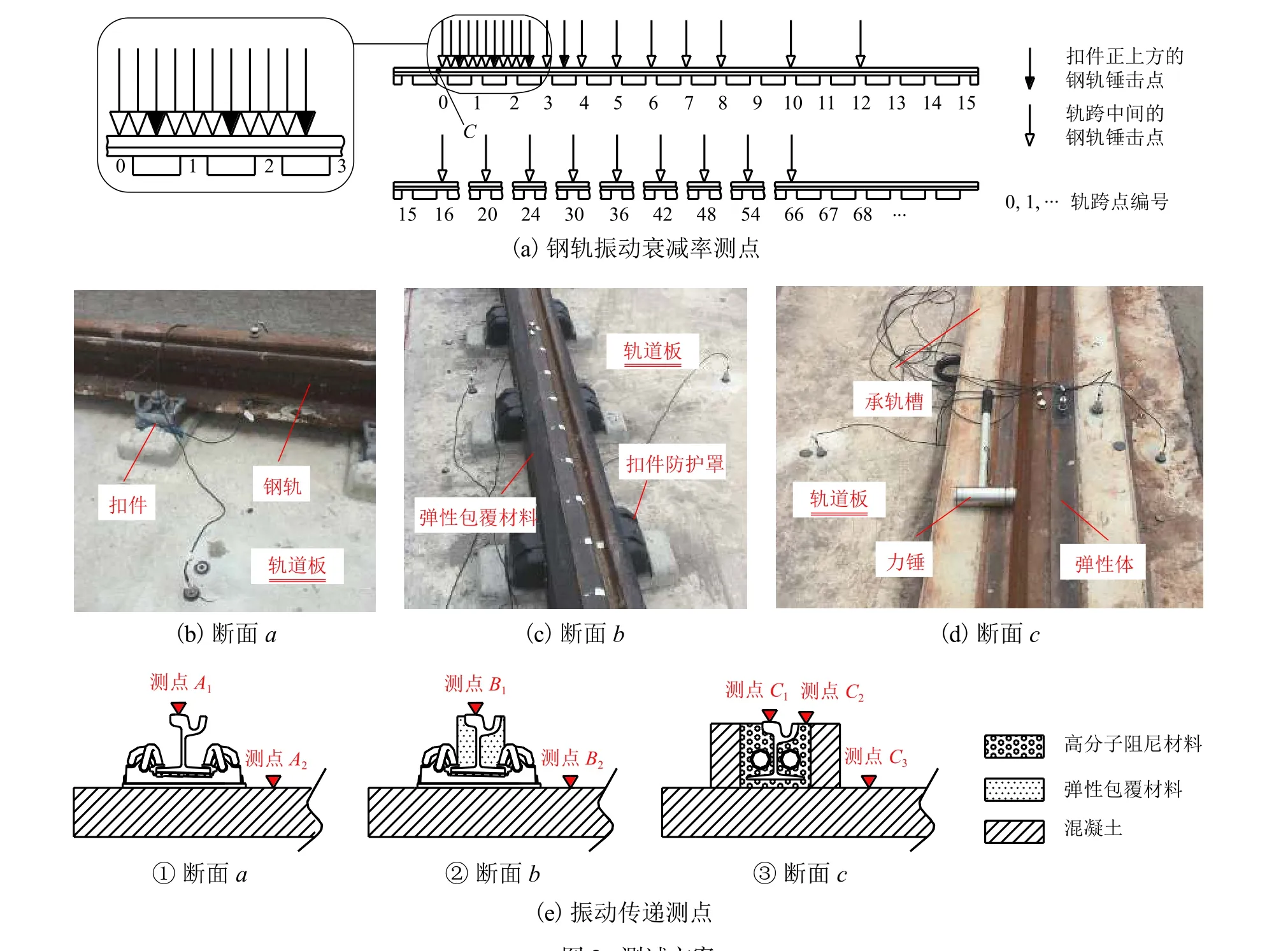
图2 测试方案Fig. 2 Measurement scheme

根据规范 BS EN 15 461: 2008 + A1: 2010[16]，钢轨振动衰减率测试中各锤击点沿钢轨纵向的布置如图2（a）所示. 加速度传感器布置在点0处（基准点），位于第1个轨跨跨中位置，即点C处. 所有锤击点按照距离基准点的远近和重要程度，可划分为测量区、近场区和远场区. 其中，测量区为点0处，该位置的频响函数作为所有试验数据的参照点，是整个测试的关键，因此锤击位置应尽可能靠近传感器安装位置. 同时，第2个轨跨跨中位置作为校核测点，布置在从点0算起的第5个锤击点处，即图2（a）中点1处正上方. 0～8号轨跨区域的锤击点组成近场区，远场区则是8号轨跨之后的所有锤击点.

本文对同一条线路上3种不同的轨道分别进行了测试，它们是未采取减振处理的普通轨道（图2（b），简称“断面a”）、安装弹性包覆材料的普通轨道（图 2（c），简称“断面b”）和嵌入式轨道（图 2（d），简称“断面c”）. 3种轨道上的振动传递测点布置如图2（e）所示，用于测试振动从钢轨到轨道板的衰减情况.

3种轨道主要部件的力学参数见表1.

在锤击试验中，应尽可能准确地标出每个锤击点的位置. 在安装传感器后，沿钢轨纵向依次测量各锤击点. 为了减小测试误差，每个锤击点应至少进行5次有效锤击，且最终的频响函数曲线应为5次有效锤击的平均值.

表1 材料参数Tab. 1 Material parameters

测试前，对所有试验设备按相关标准进行校准，以确保测试结果的有效性. 主要设备的参数如下：

1） LC0108T型加速度传感器，量程为10g，频率范围为0.35～5 000.00 Hz，灵敏度为496.00 mV/g.

2） LC0102T型加速度传感器，量程为1 000g，频率范围为2.00～13 000.00 Hz，灵敏度为5.15 mV/g.

3） LC1303B型力锤，量程为100 kN，灵敏度为0.044 7 mV/N.

4） DHDAS动态信号采集分析系统，采样频率设为12.8 kHz，同时采集加速度和锤击力信号.

2.2 数据处理

图3是断面c在力锤激励下，锤击力、钢轨振动加速度和轨道板振动加速度的典型时程曲线和频谱图. 其中，锤击点为编号6，响应点为基准点.

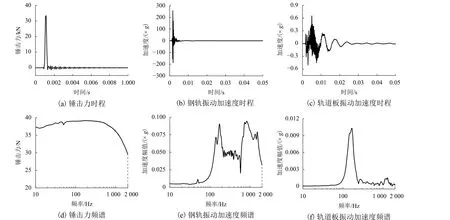
图3 典型测试样本Fig. 3 Typical test samples

从图3（a）和图3（d）能够发现，锤击力是一个持续时间很短的脉冲信号，且锤击力在2 000 Hz以内具有较大的激振能量.

从图3（b）和图3（c）可以看出，钢轨和轨道板的振动加速度随时间衰减的特征均十分明显，且钢轨的振动衰减速度明显比轨道板要大；钢轨振动加速度的峰值约为250g，轨道板振动加速度的峰值约0.6g，即从钢轨传递到轨道板的振动能量大幅度减少.

对比图 3（e）和图 3（f）可以发现，钢轨振动加速度在100～200 Hz和600～2 000 Hz频率范围内幅值较高，而轨道板振动加速度仅在100～200 Hz频段的幅值较大，这主要是由于钢轨的高频振动响应被承轨槽内的高分子阻尼材料所吸收[8-10].

3 试验结果分析

3.1 钢轨振动衰减率

钢轨受到激励后，振动能量沿钢轨两侧传递，且衰减程度与传递距离和频率有关. 以断面c为例，图4给出了测试结果的散点图，并对1/3倍频程不同频带内的钢轨振动沿线路方向的衰减规律进行了线性拟合.

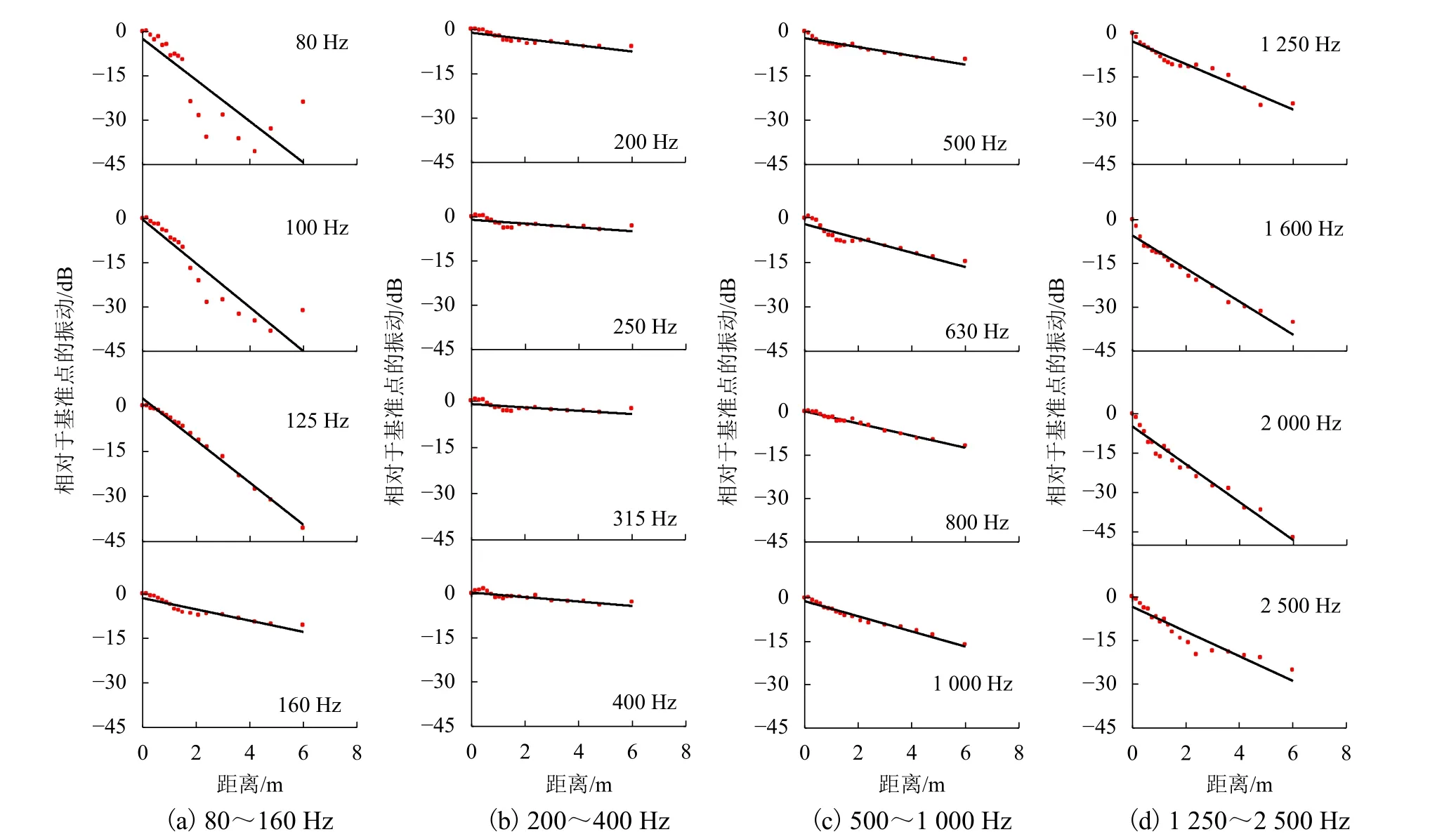
图4 钢轨振动沿线路方向的分布Fig. 4 Rail vibration distribution along track direction

从图4可以看出，钢轨振动在125 Hz频带之后随距离的衰减速度开始变慢，并在315 Hz频带附近衰减最慢；随后，钢轨振动衰减的速度逐渐开始增加，并在2 000 Hz频带附近达到最快的衰减速度.

在获得不同位置锤击时基准点处的频响函数后，再通过式（7）计算对应3种不同轨道的钢轨振动衰减率，结果示于图5中. 可以看出：

1） 对于断面 a，仅在少数几个频带（如：125、2 000 Hz）的衰减率大于1.0 dB/m，而在其余频带内的衰减率都在1.0 dB/m以下，说明沿线路方向的振动衰减非常慢.

2） 对于断面b，钢轨振动衰减率随频率变化的趋势与断面a相似. 但是，在整个频域内，断面b比断面a的钢轨振动衰减率均有显著提高，平均增大2.2倍. 由此可知，在钢轨两侧安装弹性包覆材料后，可以有效地抑制振动能量沿钢轨长度方向的传播.

3） 对于断面 c，在 1 000～3 150 Hz频带钢轨振动衰减率比较大，且比断面b更大. 钢轨振动衰减率在 1 600 Hz频带最大（≈ 5.9 dB/m），在 315 Hz频带最小. 在400 Hz以下，断面c比断面a的钢轨振动衰减率略小.

4） 总体上，在低于500 Hz时，断面b的钢轨振动衰减率最大；在高于1 000 Hz时，断面c的钢轨振动衰减率最大；在500～1 000 Hz范围，断面b和断面c的钢轨振动衰减率差异不大，但比断面a要大.

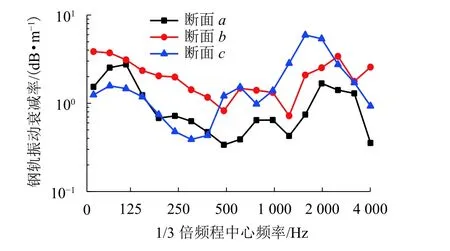
图5 钢轨振动衰减率Fig. 5 Decay rate of rails

3.2 各部件的频响特性

频响函数特征能直接反映轨道系统的固有动力特性. 在基准点处施加激励时，若锤击点与采样点重合（对于钢轨），此时获得的是直接频率响应函数.

图6给出了在基准点锤击时对应3个断面的钢轨频响函数曲线，它们均是直接频率响应函数.

图6 钢轨频响函数曲线Fig. 6 FRF curve of rails

从图6可以看出：断面a的第一个钢轨共振点出现在180 Hz附近；断面b和断面c的第1个钢轨共振点均出现在160 Hz附近，但幅值相比断面a要更低；3个断面的钢轨频响函数幅值在10～100 Hz范围差异明显，断面b最大，断面a最小；在100～160 Hz范围，断面b和断面c的钢轨频响函数幅值非常接近，且比断面a稍大；在160～2 000 Hz范围，断面a和b的钢轨频响函数幅值差异不显著，但比断面c要大.

图7给出了在基准点锤击时对应3个断面的轨道板频响函数曲线. 可以看出：3条频响函数曲线的第1个峰值频率与图6基本一致，对应了钢轨共振频率，此时断面c的轨道板频响函数最大；在整个频域内，断面a和断面b的轨道板频响函数曲线比较接近，这主要是由于轨道板测点靠近钢轨，弹性包覆材料对近场的减振效果有限；在700～2 000 Hz范围，断面c的轨道板频响函数明显小于其余两个断面，体现了高分子阻尼材料的高频减振效果优异.

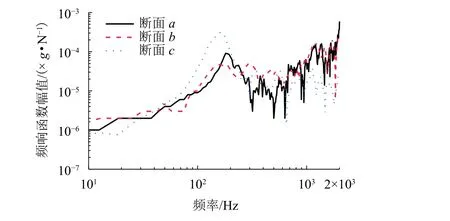
图7 轨道板频响函数曲线Fig. 7 FRF curves of track slab

针对断面c，图8对比了各部件的频响函数曲线.

对比图8发现：3个部件的第1个共振点均出现在160 Hz附近，且钢轨频响函数幅值最大（≈ 0.003 0g/N），轨道板频响函数最小（≈ 0.000 3g/N）；在500 Hz附近，弹性体（高分子阻尼材料）的频响函数要比钢轨更大，这可能是由于粘贴在弹性体上的加速度传感器的共振引起的[7]；随着频率增加（＞ 300 Hz），高分子阻尼材料的隔振效果越来越明显.

图8 嵌入式轨道各部件的频响函数曲线Fig. 8 FRF curves of all embedded rail track components

3.3 插入损失

采用插入损失可以很好地描述轨道结构采取不同措施的减振效果. 为量化减振效果，定义插入损失评价指标为

式中： Δ 的单位为dB；xdm-a为断面a在距基准点某一距离的频响函数，xdm-b,c为断面b或断面c在距基准点相同距离的频响函数.

不失一般性，以距离基准点9.6 m处的第20号锤击点的频响函数计算插入损失，结果示于图9中.根据插入损失的定义可知，若图中纵坐标数值越大，则插入损失越大，即钢轨纵向减振效果越好.

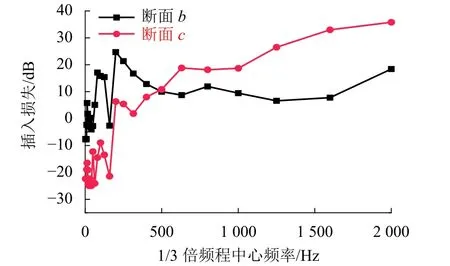
图9 插入损失对比Fig. 9 Comparison of insertion loss

由图9可知，总体上断面b和断面c的插入损失均随频率增加而逐渐增大；在10～160 Hz范围，断面c的插入损失均小于0；在50～500 Hz范围，断面b的插入损失均大于0，且比断面c要大，说明安装弹性包覆材料的普通轨道的减振效果更好；在500～2 000 Hz范围，断面c的减振效果比断面b更好，插入损失平均高13.4 dB，即嵌入式轨道对中高频振动的减振效果更好.

4 与其它减振轨道的对比

在当前的减振降噪实践中，主要措施包括钢轨减振、轨下减振和枕下减振3类[1-2]. 阻尼钢轨和钢轨吸振器是针对钢轨减振的典型措施. 轨下减振主要指各类弹性扣件，如GJ-III型、轨道减振器、Vanguard扣件等. 此外，嵌入式轨道也属于此类，其组成了一个刚度较小、衰减率较高的钢轨-扣件系统. 对于枕下减振，主要包括道砟垫、梯形轨枕轨道、浮置板轨道等，其基本原理是在枕下（或道砟下）插入一个质量-弹簧系统以隔离振动能量.

文献[17]对剪切型减振器轨道在安装调频式钢轨阻尼器（tuning rail damper，TRD）前后的钢轨振动衰减率分别进行了测试. TRD的照片如图10所示[17].剪切型减振器轨道和TRD的相关参数见表2. 需要指出的是，文献[17]中该轨道的应用场景是地铁，TRD是通过提升特定频段（200～400 Hz）扣件系统的阻尼来减小钢轨振动，进而抑制钢轨波磨的发展.

为了对比，将文献[17]与本文嵌入式轨道的测试结果如图11所示. 可以看出：与未安装TRD的剪切型减振器轨道相比，嵌入式轨道在绝大多数频带（800、4 000 Hz除外）的钢轨振动衰减率明显要大，二者的最大差值可达5.5 dB/m；与安装TRD的剪切型减振器轨道相比，嵌入式轨道的钢轨振动衰减率在1 250～3 150 Hz平均要大3.1 dB/m.

上述对比结果进一步证实，相比既有的钢轨减振和轨下减振措施，嵌入式轨道可使得高频范围（大于1 000 Hz）的钢轨振动衰减率明显提高.

图10 调频式钢轨阻尼器Fig. 10 Tuning rail damper

表2 减振轨道的技术参数Tab. 2 Technical parameters of anti-vibration tracks

图11 不同轨道系统的钢轨振动衰减率对比Fig. 11 Comparison of decay rate for different track systems

5 结 论

1） 嵌入式轨道的钢轨振动衰减率表现出明显的频率相关性. 在频率小于500 Hz时，其数值较低.在1 000～3 150 Hz范围，其数值较大，并在1 600 Hz频带达到最大值5.9 dB/m.

2） 嵌入式轨道的第1个钢轨共振点出现在频率160 Hz附近. 在大于共振频率之后，嵌入式轨道的钢轨和轨道板频响函数更低.

3） 嵌入式轨道在500～2 000 Hz范围的减振效果非常好，且比安装弹性包覆材料的普通轨道平均高13.4 dB.

4） 相比剪切型减振器轨道，嵌入式轨道在绝大多数频带的钢轨振动衰减率具有明显优势.相比安装TRD的剪切型减振器轨道，嵌入式轨道的钢轨振动衰减率在1 250～3 150 Hz范围平均要大3.1 dB/m.

通过本文的研究不难发现，嵌入式轨道具有一定的工作频段，总体上在大于500 Hz时钢轨振动衰减率更高、钢轨纵向减振效果更好. 因力锤法激励存在一定的局限性（如：激励能量小），故建议针对实际列车运行条件下嵌入式轨道的垂向减振性能进一步开展测试研究.

致谢：西南交通大学第十三期个性化实验（GX201913145）和西南交通大学大学生创新创业训练计划（190103）支持. 感谢成都市新筑路桥机械股份有限公司轨道工程公司与本文作者开展有益讨论.