灰色马尔科夫模型在建筑事故预测中的应用

周琳琳 陈 强 周银波

(1.河南省中衢建筑设计有限公司，河南 郑州 450000； 2.郑州局集团有限公司郑州工务机械段，河南 郑州 450052； 3.河南工程学院资源与安全工程学院，河南 郑州 451191)

1 研究背景

近年来，我国基础设施建设稳步发展，建筑业行业资金和人员投入也大大增加，但是我国建筑技术和管理水平仍然处在发展阶段[1]。相关数据表明，自2007年至2016年10年之间，我国建筑事故发生率和死亡率分别下降27.71%，28.66%[2]。事故发生次数整体呈下降趋势，但引发建筑事故的因素却无法避免。为了科学提高政府等部门对建筑施工的监察力度，需要对建筑事故发生次数进行预测，保障经济健康稳定发展。目前针对事故的预测方法较多，例如回归分析法、神经网络预测法、灰色预测模型、马尔科夫预测模型等，其中灰色预测模型和马尔科夫预测模型应用较多[3,4]。由于灰色预测模型应用简便，但是预测结果波动性较大，存在很大局限性，为了提高预测精度可采用马尔科夫模型对灰色预测结果进行修正。潘丽等[3]采用灰色马尔科夫模型对上海铁路客运量进行了预测，该方法可有效降低灰色模型的误差。柳子晖等[4]将该方法应用到沥青磨耗层性能预测上，对比了3种养护技术的差异。周倩倩等[5]在历年江苏冷链物流数据的基础上，对后续几年的需求量进行了预测，为江苏物流行业提供了数据参考。灰色预测法和马尔科夫模型广泛应用于随机事件的预测，建筑事故的发生受到外界因素影响较大，存在较大的波动性。单一灰色理论在该类型数据预测中误差较大，很难达到预期精度，而马尔科夫模型则能较好的描述随机变化对象的动态趋势，可以弥补灰色理论的不足。灰色马尔科夫预测模型可在实际数据的基础上，对未来状态的发展进行科学预测可在不同的领域进行应用。本文以河北省建筑事故发生统计数据为基础，采用灰色马尔科夫预测模型对事故发生的次数进行预测，为建筑施工管理提供参考。

2 模型建立

2.1 灰色模型

灰色预测模型GM(1，1)模型是一种动态预测方法，可通过累加或累减对统计数据进行处理。它的构建以原始数据序列为基础，建立过程如下：

原始序列：

X(0)=[x0(1)x0(2) …x0(n)]

(1)

累加序列：

X(1)=[x1(1)x1(2) …x1(n)]

(2)

建立具有增长趋势序列X(1)的一阶微分方程：

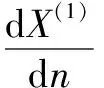
(3)

求解得到GM(1，1)模型：

(4)

(5)

式子中a,b可采用最小二乘法计算得到：

(6)

其中,

(7)

2.2 马尔科夫模型

基于随机过程理论，由马尔科夫年提出并发展而成的一种常用的预测方法，它将时间设置为随机变量，以当前状态为基础，通过状态转移矩阵来对事物发展的下一状态进行预测。通过对灰色预测GM(1，1)模型中的数据进行状态划分，假设事物发展具有n个状态，即E1，E2,…,En，建立转移概率矩阵Pn，概述事物由状态Ei随机转移到状态Ej的转移概率。样本量较少时可采用一步转换矩阵。

(8)

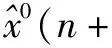
(9)

其中，N1，N2均为状态区间的边界值，当状态处于高估时取正，低估时取负。

3 预测方法在建筑事故中的应用

3.1 灰色预测模型结果

河北省建筑行业2009年—2015年事故发生统计结果见表1，数据均来自于相关事故通报[6]。

表1 河北省2009年—2015年历年建筑事故发生次数

选取2009年—2015年数据组成原始数列X(0)=[21 14 22 7 9 6 9]，根据GM(1，1)模型建立过程可得到：

X(1)=[21 35 57 64 73 79 88]

(10)

根据式(6)，式(7)和式(10)求得a=0.19，b=22.57，代入式(4)得到GM(1,1)模型：

(11)

根据灰色预测模型方程，可得到灰色预测结果如表2所示。

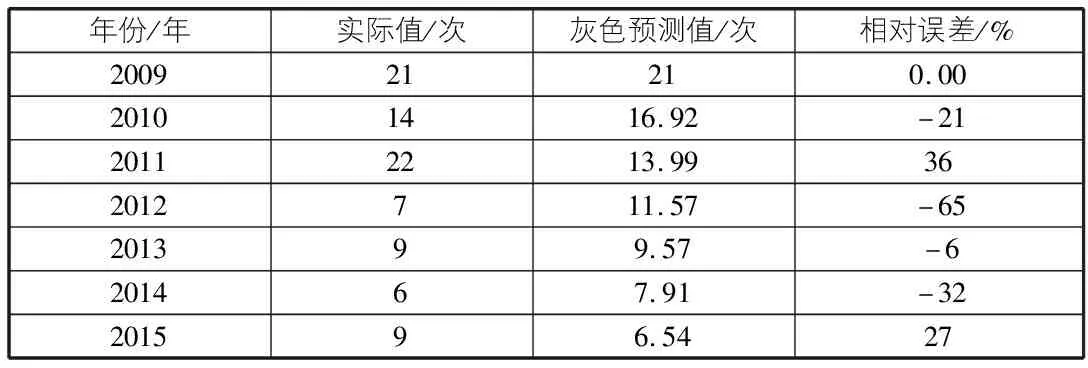
表2 河北省建筑事故发生次数灰色预测结果

3.2 马尔科夫模型修正预测值

表2中相对误差结果显示，灰色预测值与实际值之间的误差范围为(-0.65，0.36)，由于样本数较少，可将各年事故发生状态划分为三种：E1(-0.65，-0.31),E2(-0.31，0.03),E3(0.03，0.36)，得到2006年—2015年各年所处状态，见表3。

表3 2006年—2015年各年所处状态

根据表3结果，可得到一步状态转移矩阵：

(12)

根据一步转移状态矩阵，对灰色预测值采用马尔科夫修正，得到结果如表4所示。

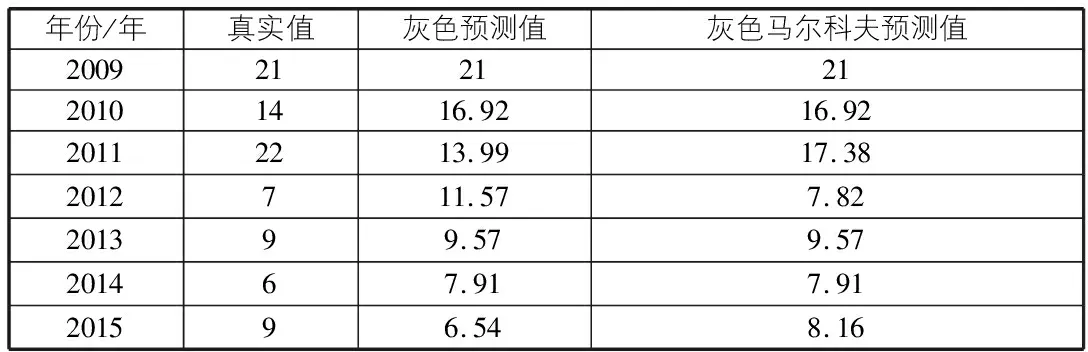
表4 模型预测结果对比

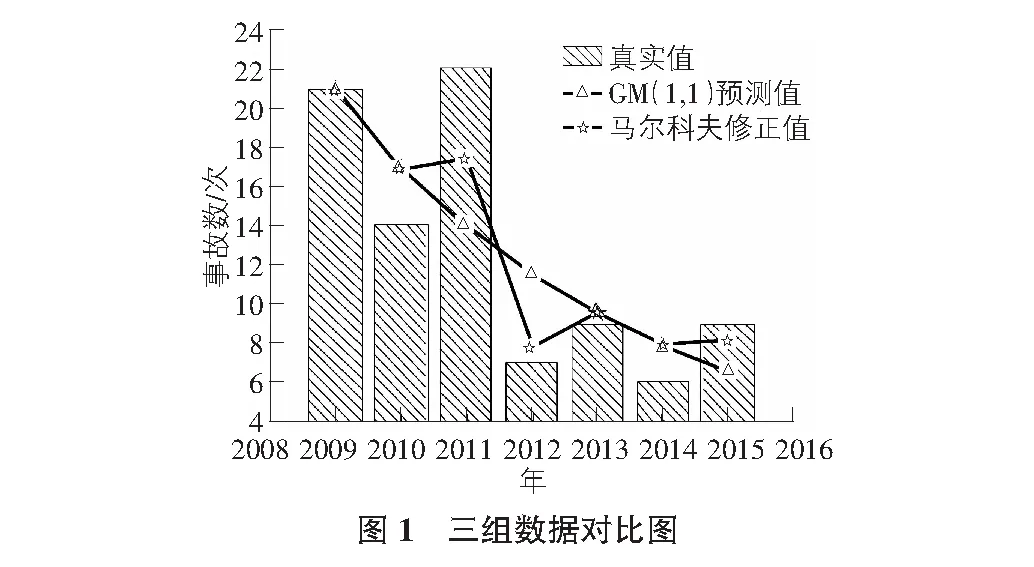
3.3 真实值、灰色预测值与马尔科夫修正值对比结果

图1对比了真实值、灰色预测值和灰色马尔科夫预测值三组数据，灰色预测结果大致呈幂函数下降趋势，与个别真实值之间误差较大，表2结果显示最大误差可达0.65。由于灰色预测模型的局限性无法对数据发展的波动性进行预测，通过采用马尔科夫模型对灰色预测模型结果进行修正可发现，在部分误差较大的数据点，修正后的灰色马尔科夫结果更加接近真实值。因此，采用灰色马尔科夫预测模型可结合两种模型优点，提高预测精度。

3.4 灰色马尔科夫预测模型对事故次数发展的预测结果

灰色马尔科夫模型在预测精度上优于灰色预测模型，在上述数据的计算基础上对2016年—2022年事故发生次数进行了进一步预测。表3显示，2015年为状态E3，根据一步转移矩阵公式得到2016年所处状态为E1，灰色预测结果为5.41，灰色马尔科夫模型预测结果为3.66。2016年事故发生次数真实值为4，可见灰色马尔科夫具有较高的预测精度。同理可得2017年—2027年河北省建筑事故发生次数的预测结果见表5。结果显示，建筑事故发生次数稳步下降，由于事故发生影响因素较多，真实情况将有所波动。通过对事故预测有利于相关部门进行参考，以便采取更加有利的措施预防事故。

表5 灰色马尔科夫对2017年—2022年建筑事故发生次数的预测结果

4 结语

1)建筑事故次数可采用灰色预测法进行初步预测，但是其误差较大，最大可达0.65，不能准确反映事故发生的发展趋势，需要提高其预测精度。

2)灰色马尔科夫模型具有更高的预测精度，预测结果能够有效的反映实际状况，河北省建筑事故次数预测结果显示，随着时间延长事故次数逐渐下降，该模型可有效反映该省的事故次数的发展趋势，可对建筑业事故发生、死亡人数等相关数据预测，为监管部门提供数据基础。