考虑润滑碰撞的精密轴承保持架动态特性
2021-02-01袁倩倩朱永生张进华杨敏燕闫柯洪军
袁倩倩,朱永生,张进华,杨敏燕,闫柯,洪军
(西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)
作为轴承重要组成部件,保持架在滚动体和引导套圈作用下运动。在变速变载复杂工况或高速条件下,滚动体容易出现打滑,引起滚动体与保持架碰撞、保持架运行不稳定、扭矩增大、轴承振动加剧[1],轴承服役性能降低,并可能导致精密机器过早失效。因此研究保持架打滑等动态特性及其影响因素,对于改善这种现象具有重要意义。
目前,诸多学者已开展了保持架动力学模型研究。在滚动体与保持架相互作用方面,周延泽等在分析保持架振动特性时发现冲击是保持架产生振动的直接原因,保持架与滚动体碰撞作用是冲击的主要来源之一,为此采用了质点与杆、梁碰撞假设,建立了保持架和滚动体碰撞模型,并分析了滚动体-保持架碰撞力影响因素[2-3]。王斌采用干摩擦碰撞模型,分析了轴承工况参数、结构参数等对保持架动态特性的影响[4]。姚廷强等忽略润滑的作用,建立了考虑保持架碰撞的球轴承动力学模型,并分析了兜孔间隙对保持架运动轨迹的影响[5]。上述模型从干摩擦碰撞分析了滚动体与保持架之间的相互作用,没有考虑滚动体与保持架之间润滑的影响。刘文秀等认为球与保持架之间的力由3部分组成:两者之间的接触载荷、流体作用力和转速不一致引起的碰撞力,并考虑润滑作用建立了滚动体与保持架的碰撞力模型,分析了保持架结构参数对保持架质心轨迹的影响,但在考虑润滑作用时只增加了润滑油膜的阻尼力,没有考虑油膜刚度[6]。刘秀海分析了润滑作用下滚动体与保持架之间的相互作用力,建立了滚动轴承的动力学分析模型,并分析了轴承结构参数及工况参数对保持架打滑及稳定性的影响,但在建立滚动体与保持架力学模型时采用了简化的Brewe公式[7]。姚譞将保持架与滚动体等效为连续碰撞系统,建立了一维不连续保持架-滚子碰撞系统模型并分析了滚动体与保持架碰撞对轴承性能的影响,但在建模时忽略了油膜的影响[8]。
在保持架动态特性影响因素研究方面,Gupta研究了保持架的运动机理,开发了轴承动力学计算程序并推出Adore软件,能够分析保持架结构参数及工况条件等对保持架稳定性的影响[9-11]。Bovet等分析轴承内部接触变形、保持架与滚道弹性流体动力接触、内部间隙和保持架跳动等多种现象,提出了一种预测大载荷下滚动轴承内部动态特性的建模方法,将预测结果与实验结果进行比较,吻合较好[12]。在上述模型的基础上,国内外学者讨论了轴承速度、保持架兜孔间隙、轴承载荷等对保持架动态特性的影响。实验结果表明,预紧力、外载荷、保持架兜孔间隙、轴承转速等是影响保持架动态特性的主要因素[13-16]。
针对目前保持架动力学分析中没有考虑润滑的问题,本文考虑轴承保持架兜孔和滚动体之间的真实润滑状态和碰撞过程,利用滚动体与保持架润滑碰撞模型建立了更为精确的保持架动力学方程。在此基础上,分析了轴承预紧力、径向载荷、内圈转速及引导-兜孔间隙比对精密轴承保持架动态特性的影响规律。
1 轴承滚动体与保持架碰撞模型
1.1 干摩擦模型
滚动体与保持架在转动过程中由于公转角速度不同会出现间歇性碰撞。滚动体与保持架之间关系如图1所示,图中平面1为轴承轴向平面,平面2为轴向平面正交的另一个主平面,Op-xpyp为保持架兜孔坐标系,Ob为滚动体中心,μ为滚动体与保持架兜孔间隙,rI1为滚动体在平面1上的曲率半径,rI2为滚动体在平面2上的曲率半径,rII2为保持架在平面2上的曲率半径。在建立球体间弹塑性正碰撞时,将碰撞过程分为弹性压缩阶段、弹塑性压缩阶段和弹性恢复阶段[17]。

图1 滚动体与保持架的位置关系
(1)弹性压缩阶段。滚动体与保持架开始接触并产生弹性作用力,使两物体的相对速度逐渐减小,同时两接触表面发生压缩变形。根据赫兹接触理论,t时刻的弹性压缩阶段滚动体动力学方程如下
(1)
式中:m和E′为滚动体与保持架的等效质量和等效弹性模量;δ为滚动体与保持架间的接触变形;κ、J1和J2为接触区的椭圆率、第一类完全椭圆积分和第二类完全椭圆积分;∑ρ为接触区曲率半径和。
弹性压缩阶段结束的标志是滚动体或保持架的接触中心达到屈服应力
(2)
式中:QC为滚动体与保持架接触碰撞载荷;a和b为椭圆接触区的长短轴半径;σp1和σp2为滚动体与保持架材料的屈服应力。
(2)弹塑性压缩阶段。当滚动体与保持架的相对速度足够大时,两物体的碰撞开始发生塑性变形,则接触区可以分为外部弹性区和内部塑性区。随着接触碰撞载荷的不断增大,两个区域的面积都不断增大,则本阶段的运动方程如下式
(3)
弹塑性压缩阶段结束的标志是两物体的相对速度减小至0,即

(4)
(3)弹性恢复阶段。滚动体与保持架在恢复力的作用下逐渐分离,相对速度开始反向增加。根据弹性压缩阶段力与位移及接触区变形,本阶段的运动方程如下式
(5)
弹性恢复阶段结束的标志是两物体的相对变形减小至塑性变形,即
δ=δp
(6)
式中δp表示滚动体与保持架间的塑性变形。
1.2 考虑润滑状态的滚动体-保持架碰撞模型
轴承滚动体与保持架之间处于半自由状态,当滚动体公转角速度与保持架公转角速度不一致时,会发生碰撞,碰撞力具有瞬时性。轴承在服役过程中,内部各零件之间存在润滑剂,滚动体与保持架接触区存在润滑油膜,润滑碰撞模型将两者之间的碰撞作用等效为刚度和阻尼系统,如图2所示,图中KT为等效刚度,CT为等效阻尼。

图2 等效碰撞模型
赵联春的研究表明,当滚动体的自旋速度远大于滚动体和保持架的相对速度时可忽略挤压运动,采用弹流润滑稳态模型即可满足计算精度[18]。润滑碰撞模型将碰撞接触区分为入口区、赫兹接触区和出口区,如图3所示,整个碰撞过程考虑了正向油膜刚度KL、赫兹接触刚度KC、入口区的油膜刚度Kef和黏性阻尼Cef的影响,U1、U2、Uz分别为滚动体自转速度、保持架转速、滚动体公转速度。

图3 润滑碰撞模型碰撞接触区
根据Dowson公式可以计算出等温条件下椭圆接触弹流中心油膜厚度hc的修正公式为
hc=2.69RU0.67G0.53W-0.067(1-0.61e-0.73κ)
(7)
式中:R为滚动体与保持架在椭圆接触区的有效半径;U为无量纲速度,U=η0us/E′R,η0为润滑剂动力黏度;us为滚动体与保持架在接触点沿滚动方向及椭圆短轴方向的平均速度;G为无量纲材料参数,G=β0E′,β0为润滑剂黏压系数;W为无量纲载荷,W=Q/E′R2。
法向接触载荷分别对接触变形和中心油膜厚度求偏导,得接触区赫兹接触刚度与正向油膜刚度为
(8)
(9)
通过分析入口区的油膜载荷与刚度和阻尼之间关系,得到入口区的油膜刚度和黏性阻尼为
(10)
(11)
由碰撞接触区的刚度和阻尼得到等效刚度和阻尼
(12)
任意时刻保持架和滚动体间运动方程为
(13)
2 轴承动力学模型及求解
2.1 碰撞模型求解过程

图4 润滑碰撞模型求解过程
步骤1:输入初始条件,包括轴承结构参数、工况条件和初始接触碰撞状态等。
步骤2:求解碰撞运动的微分方程,获得下一时刻保持架和滚动体的碰撞状态,若此时两者间相对速度小于等于0,则进入步骤3,否则重复步骤2。
步骤3:采用数值积分求解方法获得恢复阶段内任意时刻的碰撞状态,若此时两者间接触变形小于等于0,则输出最终的结果,否则重复步骤3。
2.2 轴承动力学模型及求解过程
轴承动力学模型参考文献[7],将上文建立的滚动体-保持架碰撞模型和轴承其他部件动力学模型耦合,轴承各部件运动微分方程整理如下。
(1)滚动体运动微分方程
(14)

(2)保持架运动微分方程
保持架在惯性坐标系O-XYZ中YZ平面内的运动微分方程为
(3) 试验初期,排水管壁面积的大小会影响土体梯度比Gr值下降速度。与小直径排水管壁试样相比,在大直径试样条件下,砾质黏性土下降速度变缓的时间比小直径试样早3 h,砂质黏性土早3 h,粉质黏性土早1 h。梯度比下降速度大小为:大直径排水管壁试样>小直径排水管壁试样。
(15)
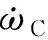
(3)内圈运动微分方程
(16)
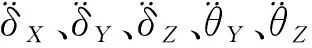
根据已知轴承参数和服役条件进行拟静力学模型计算,得到轴承各零件初始运动状态,并作为数值积分初始条件代入积分方程,采用龙格库塔法对方程组进行数值积分。
3 模型验证
3.1 保持架打滑率计算
在高速轻载等特殊工况下,由于轴承滚动体与内外圈接触点处线速度不同,导致滚动体在公转方向上打滑,滚动体打滑会引起滚道表面蹭伤和磨损,严重时导致轴承失效。保持架转动依靠套圈与滚动体产生的拖动力,当表面拖动力小于滚动体和保持架受到的各种阻力之和时,保持架实际转速便会低于理论值,发生打滑,可以通过测量保持架转速判断轴承是否发生打滑。引入打滑率来评价保持架打滑程度,打滑率越大,保持架打滑越严重。打滑率为
(17)
式中:ω为保持架理论转速[19]。
3.2 实验验证
为验证模型的正确性,搭建了保持架转速测量主轴系统实验台,如图5所示,该实验台包括激光转速传感器、反光条、信号采集系统和计算机等。实验采用的激光转速传感器型号为BK Laser Tacho Probe-MM0360,测量范围为0~3×105r/min。脉冲信号采集装置为PAK Mobile MK Ⅱ数据采集系统。将反光条粘贴在保持架端面上,激光转速传感器正对保持架端面,保持架旋转一圈返回1个脉冲信号,通过PAK Mobile MK Ⅱ数据采集系统将采集到的转速信号记录到计算机,再进行数据分析。

图5 保持架转速测量实验台
本文以国内某轴承企业设计制造的7008C/P4滚动球轴承为例,分析轴承工况参数及结构参数对保持架动态特性的影响,轴承具体参数见表1。

表1 7008C角接触球轴承的主要参数
本文将不考虑滚动体-保持架润滑(干碰撞模型)和考虑滚动体-保持架润滑(润滑碰撞模型)的仿真结果与正常润滑状态下实验结果进行对比,如图6所示,与干摩擦碰撞模型相比,考虑轴承润滑的润滑碰撞模型更接近实验结果。由图6a可以看出,干摩擦模型保持架转速最大波动量为105 r/min,润滑碰撞模型保持架转速最大波动量为52 r/min;干摩擦模型保持架平均转速比润滑模型平均转速大约低40 r/min。这是由于润滑剂具有吸振作用,使得保持架振动较小,保持架转速波动量降低。同时润滑油使保持架与引导套圈之间的摩擦阻力减小,拖动力一定的情况下,阻力减小保持架转速增大。如图6b所示,润滑碰撞模型计算的保持架打滑率更接近实验值;轴承转速为2 000 r/min时,两种碰撞模型与实验结果的保持架打滑率相差不大,最大相差0.42%;轴承转速为10 000 r/min时,两种碰撞模型与实验结果相差较大,最大相差3.25%。

(a)不同模型保持架转速

(b)不同模型保持架打滑率图6 正常润滑状态下实验与两种碰撞模型结果对比
4 结果分析
为了分析轴承工况参数、结构参数等对轴承保持架动态特性的影响,根据以上结论,润滑模型与实验结果更吻合,这里采用润滑碰撞模型进行分析。
(1)预紧力对保持架打滑率的影响。不考虑径向力,不同预紧力下保持架打滑率如图7所示,由图中可以看出:相同转速下,随着预紧力增大,保持架打滑率降低并趋于0,但不同转速预紧力对保持架打滑率影响程度不同。转速为2 000 r/min、预紧力从50 N增加到320 N时,保持架打滑率从0.37%降到0;转速为20 000 r/min、预紧力从50 N增加到320 N时,保持架打滑率从17.2%降到0.225%。低速下预紧力对保持架打滑率影响较小,高速下预紧力对保持架打滑率影响较大;低预紧、高转速时保持架打滑更严重。这是因为高速轻载条件下,由于离心力的作用,滚动体与外圈之间的作用力增大,与内圈的作用力减小,內滚道对滚动体的拖动力不足以抵消滚动体/保持架与内外圈之间的摩擦力,使滚动体发生打滑,保持架转速降低。保持架打滑率随着预紧力的增大而减小,当预紧力大于临界值300 N时,保持架打滑率很小,接近于0,因为当预紧力增加到一定程度时,滚动体和内外圈滚道之间的表面拖动力足以克服各种阻力。保持架转速趋近于理论值,即保持架的打滑率趋近于0。由此可知,足够的预紧力对防止保持架打滑具有积极的作用。

图7 预紧力对保持架打滑率的影响
(2)径向载荷对保持架打滑率的影响。当轴承预紧力为50 N时,不同径向载荷对保持架打滑率影响如图8所示,由图中可以看出:相同转速下,保持架打滑率随径向载荷的增大而减小。径向载荷对保持架打滑的影响程度受轴承转速的影响,如轴承内圈转速为8 000 r/min时,径向载荷从0 N增加到1 000 N,保持架打滑率从2.93%下降到1.69%;轴承内圈转速为20 000 r/min时,径向载荷从0 N增加到1 000 N,保持架打滑率从17.2%下降到2.84%。高速下,径向载荷对保持架打滑率的影响程度较大。与预紧力相比,相同力变化区间,预紧力对保持架打滑的影响更大。这是由于相同转速下,径向载荷越大滚道对滚动体的总拖动力越大,保持架转速越高;当径向载荷增大到一定程度,滚动体与滚道间接触力增大,滚动体与内外滚道间接触变形增大,削弱了离心力对滚动体与內滚道接触力的影响,内滚道对滚动体的拖动力可以克服滚动体和保持架受到的总阻力,滚动体与滚道之间出现轻微打滑,保持架转速接近理论转速,打滑率降低。

图8 径向载荷对保持架打滑率的影响
(3)轴承内圈转速对保持架打滑率的影响。不考虑径向载荷,轴承微预紧力为50 N、轻预紧力为100 N、中预紧力为300 N 3种预紧状态时,内圈转速对保持架打滑率的影响如图9所示,由图中可以看出:预紧力一定的情况下,内圈转速越高保持架打滑率越大;不同的预紧力下,内圈转速对保持架打滑率的影响程度不同,微预紧下,转速对保持架打滑率的影响程度最大。微预紧下,随着内圈转速增大打滑率增加,高达16.8%;轻预紧下,随着内圈转速增大打滑率增加10.5%;中预紧下,随着内圈转速增大打滑率仅增加0.23%。这是由于3种预紧中微预紧滚动体与内外圈之间接触载荷最小,拖动力最小,随着内圈转速增大,滚动体受到离心力增大,滚动体与内圈之间拖动力减小,打滑率增大。适当提高预紧力可以抑制内圈转速对保持架打滑率的影响。

图9 内圈转速对保持架打滑率的影响
(4)结构参数对保持架打滑率的影响。保持架在滚动轴承中主要受到滚动体的碰撞力以及与引导面之间的接触摩擦力,因此引导间隙和兜孔间隙会对保持架性能造成重要影响。轴承预紧力为50 N、径向载荷为500 N、内圈转速为10 000 r/min、轴承其他结构参数不变时,引导间隙-兜孔间隙比对保持架平均转速及打滑率的影响如图10所示。由图中可以看出:当引导-兜孔间隙比从0.5增加到2时,保持架打滑率从4.05%降到2.18%,保持架转速增加。减小兜孔间隙或增大引导间隙能提高保持架平均转速,降低打滑率。这是由于单独减小兜孔间隙或增大引导间隙,都会使保持架和引导套圈之间的拖动力增加,引起保持架转速增加,打滑率下降。兜孔间隙过小使滚动体与保持架间摩擦发热增大,轴承温度升高,考虑轴承工况条件、润滑剂等,保证轴承使用性能的前提下,应尽量增大引导-兜孔间隙比。

图10 引导-兜孔间隙比对保持架平均转速及打滑率的影响
5 结 论
保持架在引导套圈和滚动体耦合作用下产生随机运动,其动态特性影响精密轴承的服役性能。为了准确分析保持架的动态特性,本文考虑轴承保持架兜孔和滚动体之间的真实润滑状态和碰撞过程,建立了保持架精确动力学模型,分析了轴承预紧力、径向载荷、内圈转速及引导-兜孔间隙比对精密轴承保持架动态特性的影响规律,得到如下结论。
(1)考虑润滑的保持架动态特性分析结果与实验结果更吻合。与保持架兜孔-滚动体干摩擦模型相比,考虑润滑的保持架平均转速更高,打滑率更低,更接近理论值和实验值;考虑润滑的保持架转速波动量相比传统模型更低,轴承内圈转速影响保持架打滑率。
(2)轴承外载荷影响保持架动态特性,随着轴承预紧力的增大保持架打滑率减小最终趋于0,不同转速下,轴承预紧力对保持架打滑程度的影响不同,高转速低预紧力保持架更容易打滑,在高速下要适当增加预紧力来抑制打滑。随着轴承径向载荷增大,保持架打滑率减小,高速下径向载荷改变比低速下对保持架打滑影响更大。相比径向载荷,预紧力对保持架打滑影响更大。相同预紧状态下,随着内圈转速增加,保持架打滑率增大;3种预紧状态中,中预紧时转速对保持架打滑影响最小。
(3)随着引导间隙-兜孔间隙比的增加,保持架转速增加,打滑率降低。
