基于VLBI的高精度定位
2021-01-30李金岭王广利郑为民
郭 丽,张 宇,李金岭,王广利,郑为民,3
(1.中国科学院 上海天文台,上海 200030;2.武汉大学 卫星导航定位技术研究中心,430079;3.上海市空间导航与定位技术重点实验室,上海,200030)
引 言
深空目标的轨道计算和定位归算既有相通之处,也存在显著区别。主要区别在于,定轨计算一般要求有足够长的跟踪弧段,通过状态转移矩阵将整个弧段中不同时刻的观测资料联系起来统一求解,强调精确模制整个跟踪弧段中飞行器的动力学状态。而在定位归算中,待求参数是各给定时刻目标的位置,对跟踪弧段的长度没有苛刻要求,不需要模制飞行器的受力状况,仅依据测站与目标的几何关系实现轨迹确定。在轨道机动、软着陆以及月面行进等过程中,由于目标的受力状态不易精确模制,一般可采用定位归算,以快速确定目标飞行或行进轨迹。
我国探月工程和火星探测工程中,采用USB(United S-band)/UXB(United X-band)测距测速技术与VLBI两种手段进行联合测定轨工作[1-2]。VLBI测轨分系统由上海处理中心和位于上海、北京、昆明和乌鲁木齐的VLBI台站组成[3]。VLBI测轨分系统根据VLBI各台站的观测数据,实时给出该网的时延和时延率观测量,并将综合利用VLBI测量结果、测距测速数据对探测器各飞行段的定轨定位和轨道预报等发往北京中心。定位归算是VLBI测轨分系统的软件配置项之一[4],可快速实时给出探测器的位置信息。
在“嫦娥1号”任务期间,定位归算在月球捕获、受控撞月等关键弧段已经获得了成功应用。在“嫦娥2号”探测器的中途轨道修正、月球捕获和数次绕月轨道机动中,定位归算也成功应用于探测器轨迹的实时监测。“嫦娥4号”(CE-4)首次成功实现了月球背面软着陆和探测任务[2-12]。CE-4包括中继星和着巡组合体(以下简称着巡体),其中着巡体在月球背面着陆并开始探测,中继星在地月L2点的Halo轨道上运行,开展地月之间的信息传输。
本文将介绍实时模式下,VLBI在S、X波段单点定位的精度情况分析、在轨道机制和探测器被月球捕获阶段的轨道根数实时监测,在关键任务阶段,如轨道制动和探测器被捕获阶段定位归算实时确定探测器的轨道信息、准实时模式下,采用统计联合定位方法以及月面高程约束方法,进一步压制和降低噪声影响,提高月面的着陆器和巡视器位置信息精度,及时快速确定探测器的这些位置信息。
1 VLBI实时定位归算精度
定位归算即假设测站的坐标与运动以及地球定向参数(Earth Orbit Plane,EOP)均准确已知,设法从探测器信号同一波前观测量(VLBI时延、时延率、USB测距测速)中解析出信号发出时刻的探测器状态矢量(三维坐标与速度)。时延和测距仅是探测器坐标的函数,时延率和测速则同时取决于探测器的坐标与速度。为提高参数解的收敛速度,探测器坐标与速度的初值一般取自预报轨道,且越准确越好。若仅解算探测器坐标相对于初值的改正,一般只利用时延、测距观测量。延迟率和测速观测量对探测器坐标的约束作用相对较低,且速度初值的偏差会影响坐标改正的解算精度。
定位中采用的观测数据是实时的VLBI时延和测距两类数据,两者满足的观测方程为
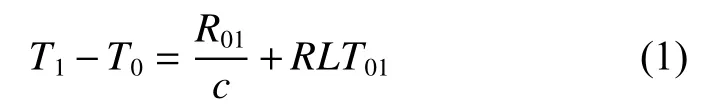
式(1)是在太阳系质心坐标系(Barycentric Celestial Reference System,BCRS)下,信号从探测器到台站1的光行时[13],等式右边第1项是探测器和台站1在响应时刻的距离与光速的比值,第2项是该项的相对论修正,通过对光行时的迭代计算可以得到探测器到达台站1和台站2的精确光行时,在BCRS下的时延即为两者的差,对于单程测距而言,测距值即为探测器到达台站1的精确光行时。时延观测量需要将TDB转换到TT时间系统,转换满足的方程为
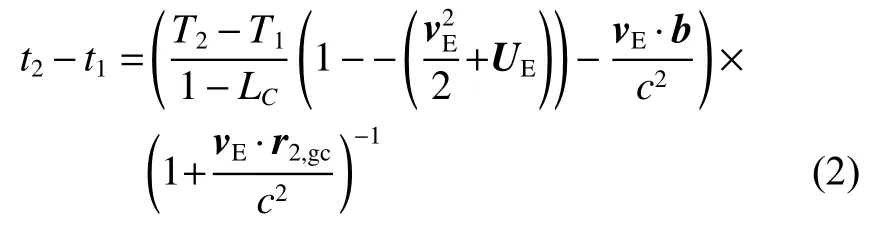
建立了观测方程得到时延和测距的理论值,通过内插得到对应于同一星上时刻的观测量后得到o-c的值,通过偏导数的解算[5],构建最小二乘方程,解算探测器的实时位置。定位归算中,不一定正好存在与给定时刻波前相对应的观测量,需依据探测器坐标采用值迭代计算所需观测量的观测时刻,进而由观测序列内插出所观测量。这与坐标初值改正的解算是一个循环和逐步逼近的过程。
2 月球探测实时单点定位精度
在月球探测中,VLBI主要是在S波段或者X波段上开展观测,其中CE-1、CE-2、CE-4中继星均在S波段,CE-3、CE-4着陆器在X波段上,“嫦娥5号”再入返回飞行试验器(CE-5T1)是在S/X双频波段上开展VLBI观测。相比于S波段,X波段上射电干扰少,电离层的误差也相对较小,测量精度相对较高。
CE-4中继星尽管也是主要在S波段观测,但是与CE-3一样,利用的是ΔDOR差分VLBI技术。在实时模式下,对探测器和其附近位置精确已知的射电源交替观测,修正相关系统误差,从而获得高精度观测量。CE-4中继星的VLBI时延测量数据定轨后残差相较CE-3的X频段数据精度略有下降,但是精度高于CE-2和CE-5T1任务[12]。
由于VLBI观测的波段不同及ΔDOR技术的采用等,定位归算得到的探测器位置精度也相应有所变化。本文将以CE-4任务的观测为例给出定位归算的精度情况。实时任务期间,定位归算除了实时测定探测器的位置外,还实时监视时延和测距数据情况,通过实时的拟前和拟后残差结果,实时判断轨道状态,及时准确地确定轨道情况。
图1和图2是CE-4探测器实时任务s8512a(代码表示S波段2018年5月12日第一次实验)实验期间测量数据拟合前后的情况,实时定位结果前观测量O与基于预报星历推算的时延(图1)和测距(图2)的拟前残差(红色所示),观测量O与定位结果后得到的探测器位置推算的时延(图1)和测距(图2)的拟后残差(绿色所示)。图3所示为在s8512a实验中,实时定位与预报轨道在赤经赤纬方向上的差异。
由图1~3可以明显看出,此次实验中进行了轨道制动,并且快速判断出制动的开始和结束时刻。以CE-4中继星任务为例(图4)显示实时定位的精度,蓝色为赤经精度统计,紫色为赤纬精度统计。可见,该精度远好于项目指标的要求精度(赤经0.05~0.37 as,赤纬0.07~0.40 as)。
3 轨控弧段定位归算
3.1 月球捕获阶段的轨道监测分析
在探月工程中,探测器在到达目标轨道之前,中途会进行多次轨道修正,比如在探测器抵达月球轨道附近,被月球捕获阶段,需要进行轨道机动。在非轨道机动阶段,轨道根数通常都是相对稳定的,通过对一段时间内所有测量数据的动力学轨道拟合和参数化的定轨计算,获得高精度的轨道参数。在轨道机动阶段,探测器受力情况复杂,除了常规摄动力外,轨道制动量随时可能发生变化,在此阶段的轨道根数实时发生变化,无法通过常规定轨方法给出。
定位归算是基于探测器与地面测站网的相对几何关系,不受探测器具体的受力情况影响,基于实时的VLBI时延、时延率以及测距测速观测量,实时解算探测器的位置和速度参数,进而实时获取6个瞬时轨道根数。因此在轨道制动阶段包括变轨过程、探测器被月球捕获阶段,以及在CE-4中继星变轨进入halo轨道阶段,实时定位方法快速地给出轨道信息,为工程提供参考,包括判断轨道机动效果和制定进一步轨道机动计划,以及判断探测器是否已被捕获或到达预订轨道等。

图1 CE-4中继星s8c12a实验中时延拟合前后残差Fig.1 The pre-fit and post-fit of delay residuals in s8c12a experiment of CE-4 relay satellite project

图2 CE-4中继星s8c12a实验中测距拟合前后残差Fig.2 The pre-fit and post-fit of range residuals in s8c12a experiment of CE-4 relay satellite project

图3 CE-4的s8c12a实验中实时定位结果与预报轨道的差异Fig.3 The differences between the positioning results in real-time and the orbit prediction in experiment s8c12a of CE-4 project
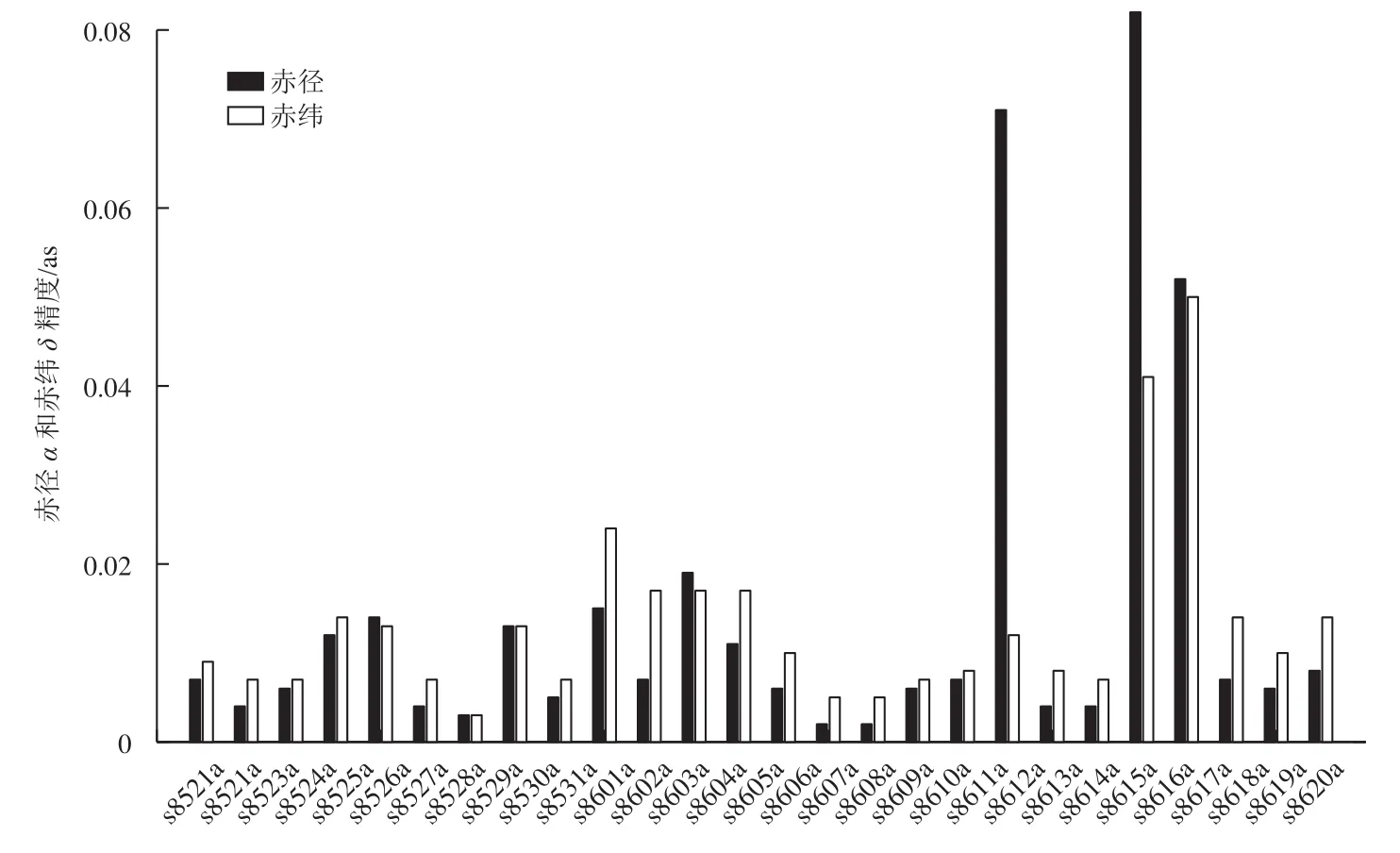
图4 CE-4中继星任务中定位精度的统计Fig.4 The position precision statistics in CE-4 relay satellite project
相比于实时单点定位,实时轨道监测还需要同时解算探测器的速度,因此,除了读取时延和测距数据外,还要借助于时延率和Doppler观测数据对速度进行解算,观测方程基于式(1)和式(2)建立起其时间差分量。同理,解算时延率和Doppler对位置速度的偏导数,构建最小二乘方程,同时解算探测器的位置和速度6维坐标,然后将其转换成轨道根数,式(3)和式(4)是由探测器的位置 r 和速度v 得 到半长径a 和偏心率 e 的方程,其中µ 是引力常数。
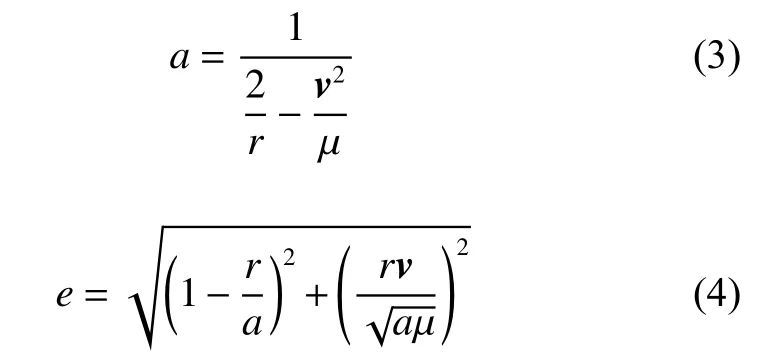
随着探测器与地月距离的变化,中心引力天体也发生变化,当距离月心小于66 200 km时,将进入月球引力范围,中心天体由地球转为月球。轨道也相应变成以月心为焦点的双曲线轨道。在2019年5月25日CE-4中继星进行了近月制动,表1给出中继星在近月制动时轨道偏心率的变化。由表1可以看出,在轨道制动的17 min内,轨道偏心率从1.303逐渐减小到0.966并稳定下来,由偏心率大于1的双曲线轨道转变为偏心率小于1的椭圆轨道,说明中继星成功被月球捕获。这是判断轨道机动效果的重要依据,也是工程成败的关键性标识。

表1 CE-4中继星近月捕获期间的偏心率变化Table 1 Eccentricity changes of CE-4 relay satellite during the baking at perilune
3.2 中继星进入Halo轨道的实时监测分析
CE-4任务中着巡体成功实现了人类历史上首次月球背面软着陆,并开展了一系列月球背面的就位探测与巡视探测。运行在地月拉格朗日L2动力学平动点附近的CE-4中继星探测器,为月球背面的着巡体探测器与地球之间提供了通讯联系,降低了轨道转移的燃料消耗,也延长了其轨运行寿命。CE-4中继星在绕L2平动点的Halo轨道上运行,Halo轨道不是通常探测器的椭圆轨道,而是三维的非规则曲线,轨道控制比较复杂[7-9]。CE-4中继星在Halo轨道做周期运动,通过定期轨控保持轨道的稳定性。在CE-4中继星进入Halo轨道前后,将实时定位归算的结果转化为瞬时轨道根数,通过轨道根数的变化判断是否成功变轨,用变轨后的定轨结果与定位归算结果比较判断是否正确进入Halo轨道。
2019年6月14日3时,中继星进行了第二次捕获机动,之后将变轨进入Halo轨道[10]。图5为变轨前后轨道根数的情况。从轨道制动开始的7 min内,中继星轨道根数出现明显变化,之后轨道根数基本保持不变,通过事后与项目指标比对,表明此次中继星在预定时间顺利完成变轨任务。

图5 CE-4中继星进入Halo轨道前后的轨道根数变化情况Fig.5 Orbital elements change during the CE-4 relay satellite entering the Halo orbit
4 月面着陆器与巡视器的准实时定位
在测定轨任务期间,定位归算实时性强,从得到观测数据至给出定位结果,定位配置项的总时间响应要求小于7.5 s,并快速给出探测器的三维位置结果;在轨道制动阶段,也实时给出高精度的瞬时轨道根数,以便监测轨道的实时状态,为工程提供重要参考。在CE-3及后续发射的CE-5任务中,将对月面目标如CE-3着陆器和巡视器以及CE-5着陆器进行定位,对这类探测器的定位模式与实时定位有所不同,月面目标的定位属于准实时的响应。因为着陆器在月面固定不动,巡视器在一段时间内也在月面上保持静止,通过积累这段时间的测量数据,采用统计联合定位模式,增加了有效观测数据的长度,压缩噪声影响,进而提高定位精度[12]。
4.1 月面着陆器定位
相比于在奔月和环月段的实时单点定位,在月面着陆器的定位中,观测方程的偏导数增加了天球坐标系到月固坐标系的转换矩阵,由两个坐标系转换的欧拉角旋转矩阵予以实现[10]。CE-3着陆器于2013年12月14日成功软着陆于月球的虹湾区域,在CE-3着陆后的1 h内,基于测轨系统提供的VLBI时延和UXB三向测距数据,进行着陆器统计联合定位计算。
月固坐标系有主轴和平轴坐标系两类,美国喷气推进实验室(Jet Propulsion Laboratory,JPL)的DE历表(采用DE421历表)能够提供转换到主轴坐标系的欧拉角[11-12],为比较结果方便,项目要求统一采用平轴坐标系,因此,CE-3着陆器定位结果统一在平轴坐标系中描述。
基于美国的月球探测器(Lunar Reconnaissance Orbiter,LRO)的激光测高数据编制的2 050阶月球地形球谐函数模型,整体精度优于10 m[11],而CE-3着陆器的位置在月球的虹湾区域,这里地势平坦,该模型的精度更高,并且,该模型也是在平轴坐标系中描述的[12-14]。因此为了提高着陆器的定位精度,利用了高程约束,测量模型为

其中:x,y,z是月固系下着陆器的坐标; r0是月球半径;r ( λ,φ)是以经纬度为函数的着陆器高程,通过读取LRO的模型获取;ϵ 是噪声。
基于式(5),得到CE-3在平轴月固坐标系下的着陆器的位置为经度-19.507 78°,纬度44.122 36°,高程-2 634 m,该位置与NASA采用的LRO探测器成像得到的三维位置差异小于100 m,与其它方法得到的三维位置差异也在100 m以内[12]。这对于38 400 km以远目标,仅相当于0.05 as的角误差。
CE-5探测器于2020年11月发射,完成我国首次月球月壤采样返回任务。CE-5的着陆器与上升器的组合体在月球北风暴洋的Rümker区着陆,采集了月面及地下的月壤后,上升器与着陆器分离,在月面点火上升器起飞,后与返回器对接,共同返回地球。因此,CE-5着陆器的定位精度尤为重要,也进行了CE-5着陆器的定位仿真与精度分析。
仿真产生CE-5着陆器的理论位置(按照CE-3着陆器的坐标形式给出)。仿真数据包括4个VLBI站的时延数据和3个台站的测距数据,仿真的噪声为时延1 ns,测距为0.5 m,结合项目的情况,仅采用0.5 h的观测数据定位,得到的仿真定位结果三维总的差异为31.6 m。满足项目精度要求。
4.2 月面巡视器定位
CE-3在巡视器和着陆器成功分离后,巡视器绕着陆器行走并在多点停留,与着陆器互拍,巡视器停留时,VLBI测轨分系统对巡视器和着陆器进行了同波束的测量,测量包括巡视器相对于着陆器的同波束差分群时延和差分相时延观测数据,其中差分相时延消除了共同的大气、电离层和仪器差等误差,大大提高了观测量的精度,但是存在整周模糊度,在定位中同时解算巡视器相对于着陆器的位置及模糊度参数。
定位中采用的是着陆器北东地坐标系下的北、东向的相对位置

其中,全局量 ε0为某基线的时延系统差(整周模糊度反映在观测量里),右侧第1项为差分时延对惯性系下巡视器位置的偏导数;第2项时惯性坐标系下的巡视器位置相对于月固系下位置的偏导数;第3项是月固系下三维位置对北东地坐标的偏导数,这里没有求解高程,因为虹湾区域地势平缓,并且两者相距仅几十m,将巡视器的高程约束到着陆器上。
通过采用统计联合方法,在高程约束下,定位归算得到了巡视器相对于着陆器的位置,采用同波束差分相时延可以获得1 m外部符合(相比于照相技术和成图技术)的相对定位精度[12]。该方法简洁、精度高,可以和照相相互比较验证。
5 结 论
本文主要介绍了我国探月工程嫦娥系列探测器项目中的定位应用。实时定位准确快速确定探测器的三维位置信息,在特殊的轨道制动阶段,如变轨、近月制动、捕获机动等,通过实时分析VLBI时延、时延率及测距和Doppler数据解析探测器的6维状态参数,并转换为瞬时轨道根数,快速准确地判断瞬时轨道,为工程提供重要参考。
准实时模式下针对月面的着陆器和巡视器定位,能够获得全部数据时,快速响应,采用联合统计定位方法以及高程约束,进一步压制噪声影响,获得了着陆器好于100 m的外部符合精度。基于高精度的VLBI同波束差分相时延观测量,实现了对巡视器外部符合1 m的高精度相对定位。
我国已发射的CE-5探测器,实现了月面软着陆及返回两大工程目标,并且也实现了上升器与返回器的交汇对接。在两个探测器的交汇对接期间,定位归算也将实时快速直观确定两个探测器的差分位置,将继续发展定位归算方法。
