过水巷道中骨料起动力学机制及两相流耦合模拟

牟 林

过水巷道中骨料起动力学机制及两相流耦合模拟

牟 林1,2

(1. 煤炭科学研究总院，北京 100013；2. 中煤科工集团西安研究院有限公司，陕西 西安 710077)

为研究动水巷道中骨料堆积状态与巷道倾角的内在关系，建立动水环境不同倾角巷道中骨料颗粒的起动判据，基于计算流体力学和离散元法建立描述骨料灌注过程的固液两相流耦合模型(CFD–DEM)，对5~10 mm、10~30 mm、30~50 mm骨料颗粒组在不同堆积厚度下的起动速度和水流携砂能力进行测试，并模拟各粒径颗粒组在不同倾角巷道中的静水休止角和动水运移规律。结果表明：起动速度在上山巷道、水平巷道、下山巷道依次减小，3种工况下骨料起动速度的平方之比值为：(tancos+sin)︰tan︰(tancos–sin)；堆积体形态由流场与灌注能力的动态平衡状态所决定，当流场的携砂能力远小于灌注能力时接顶容易，反之接顶困难；巷道倾角对堆积体相对于水平线的休止角没有影响，在相同流速条件下骨料在下山巷道中堆积形态被“拉长”不易接顶，上山巷道中被“压缩”相对容易接顶；上山段截流可降低施工难度，截流位置确定后应根据巷道倾角实时调整灌注参数，下山巷道骨料粒径适当增加，上山相应减小，使堆积长度和高度同步“生长”实现快速截流。研究成果对截流工程选址和骨料灌注参数设定具有重要指导意义。

CFD-DEM；骨料灌注；动水巷道；截流工程；固–液两相流

矿井发生突水淹井后，采用截流方法切断水源与矿井间的水力联系，是实现快速救援和排水复矿的重要方法[1]。由于施工过程具有一定隐蔽性，动水骨料灌注截流技术使截流阻水墙的建造长期处于经验摸索状态[2–8]。灌注过程中骨料随动水搬运、堆积而成的状态是影响截流进度的关键因素，巷道倾角对骨料堆积形态和灌注量有直接影响，研究其作用机制对认识截流过程有重要意义。

为研究骨料灌注过程，李维欣[9]、惠爽[10]设计多孔灌注可视化试验模型，对骨料截流过程中的影响因素进行探讨，从定性角度研究骨料灌注截流过程。骨料在水流中的运移过程，本质上为固–液两相流耦合问题，近年来采用计算流体动力学(CFD)和离散单元法(DEM)相结合求解两相流问题的方法已受到广泛关注(简称CFD-DEM)。在岩土工程领域，U. EI Shamy等[11]首次采用该方法分析土坡渗流问题及饱和土体振动液化问题，获得较好的结果；周健等[12–13]、罗勇等[14]、王胤等[15]和蒋明镜等[16]采用类似的思路开展土体渗流及液化问题的研究。骨料运移属于流化床问题，景路等[17]模拟水下滑坡坍塌过程，描述海底边坡的失稳、流动和堆积过程；刘卡等[18]分析水下抛石初始速度、粒径、密度因素对抛石运动规律的影响；苏东升[19]模拟泥沙沉降、明渠水流泥沙运动过程，研究流体运动特征及颗粒迁移分布形式；邵兵等[20]对大粒径非常规岩屑在水平井段的运移规律进行模拟，得出颗粒形状对钻井液携岩效果的影响；黄文博等[21]验证了CFD-DEM方法对求解非均匀直管填充床压降相对传统方法误差更小。以往研究工作验证CFD-DEM两相流耦合方法具有广泛的应用前景，为动水中骨料运移模型的建立提供数值计算手段，而在煤矿水害防治领域采用类似方法进行截流工程计算的研究鲜见报道，其适用性有待进一步验证。

本文通过理论分析骨料颗粒在巷道中的起动判据，采用CFD软件FLUENT描述水流运动特征，骨料颗粒系统运动状态采用DEM软件EDEM求解，通过二者间的耦合计算实现骨料灌注过程的数值仿真，研究巷道倾角对骨料堆积形态及截流过程的影响特征，探讨阻水墙建造的选址方法，对工程施工具有一定理论指导意义。

1 骨料颗粒的起动机制分析

1.1 水平巷道骨料颗粒受力分析

如图1所示，巷道中骨料颗粒为无黏性颗粒，受到的作用力主要包括拖曳力、有效重力和上举力[22]，计算公式如下：

图1 水平巷道骨料受力状态

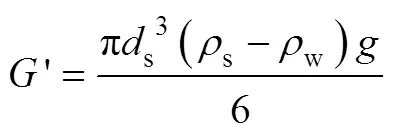
颗粒起动的临界条件：

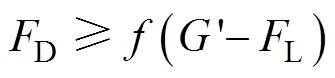
将式(1)—式(3)代入式(4)得到水平起动速度：

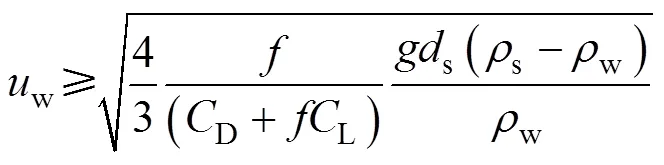
式(5)能直观反映出起动速度与颗粒粒径呈现正相关，颗粒粒径越大，起动速度越大。

1.2 上山巷道骨料颗粒受力分析

如图2所示，有效重力垂直于运动方向的分量：

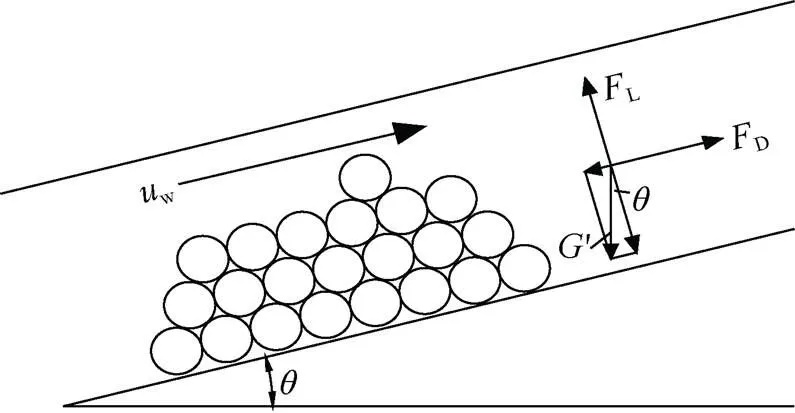
图2 上山巷道骨料受力状态

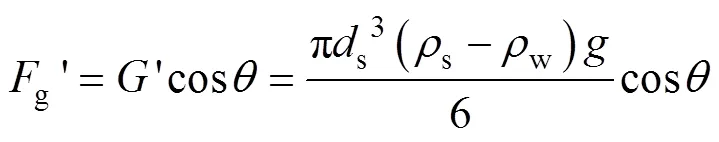
有效重力平行于运动方向的分量：

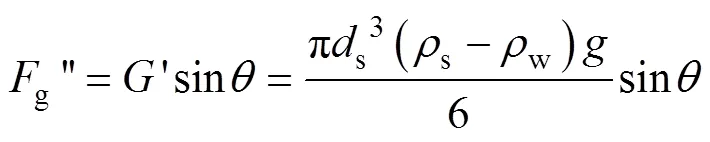
颗粒起动的临界条件：

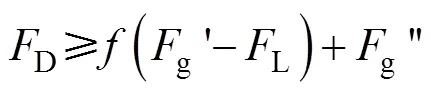
将式(6)—式(7)和式(2)—式(3)代入式(8)得到上山起动速度：

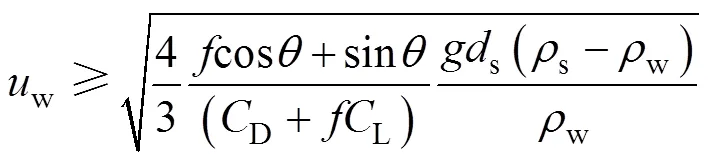
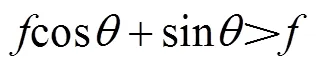
将式(10)进行三角变换可得到：

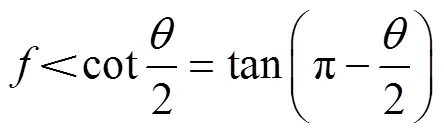
1.3 下山巷道骨料颗粒受力分析

如图3所示，有效重力垂直于运动方向的分量：

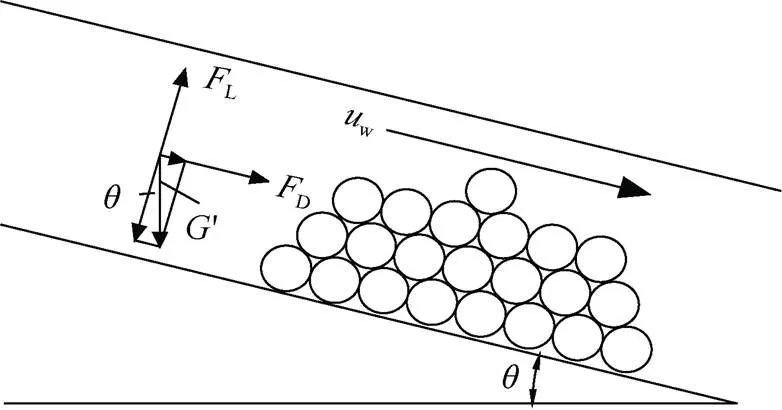
图3 下山巷道骨料受力状态

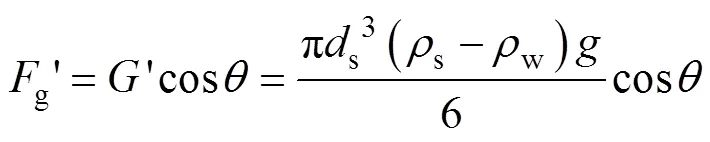
有效重力平行于运动方向的分量：

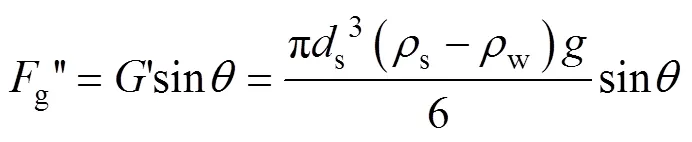
颗粒起动的临界条件：

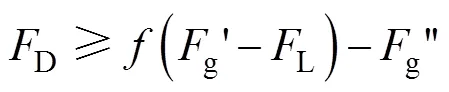
将式(12)—式(13)和式(2)—式(3)代入式(14)得到下山巷道起动速度：

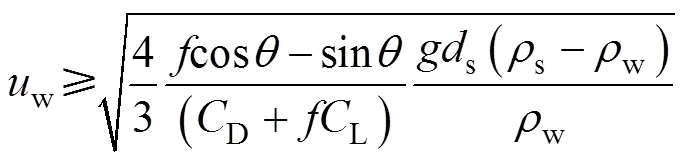
在下山巷道中，除拖曳力外，重力往下山方向的分量也组成驱动颗粒运动的力，从而导致重力垂直于流速方向的分量变小，即阻力变小。

1.4 起动速度的差异性分析

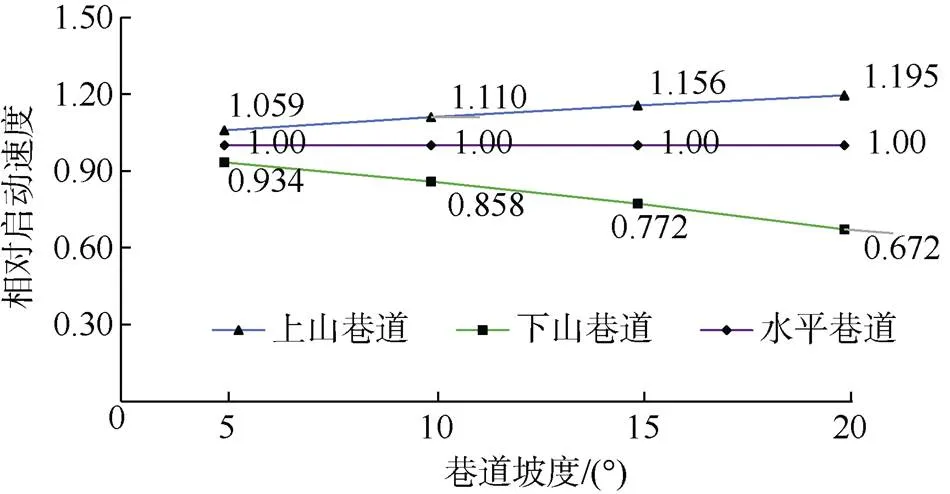
图4 骨料颗粒相对起动速度与坡度的关系

2 骨料堆积过程的流固耦合数值模拟

2.1 CFD-EDEM耦合参数设定

本文模型的模拟参数如下：模拟环境为清水，密度998.2 kg/m3，运动黏度10–6m2/s，颗粒采用Hertz-Mindlin“软球”模型，弹性模量5×106Pa，泊松比0.3，恢复系数0.3，滑动摩擦因数0.1，颗粒密度2 650 kg/m³。

2.2 骨料的有效起动流速

计算模型采用长200 cm、宽50 cm、高50 cm的模拟巷道，网格划分采用2 cm六面体，颗粒沿模型长轴起点开始运动至终点流出。令max为颗粒组最大粒径，以 5~10 mm颗粒组为例测试在1~2倍max和3~5倍max2种堆积厚度下的起动状态。厚度1~2倍max代表初期投料时骨料直接触底的情形，3~5倍max代表堆积达到一定厚度后骨料在已有颗粒表面滚动的情形。当水流流速大于一定值，颗粒组产生明显速度，其运动距离对堆积过程不可忽略时的流速可视为有效起动流速。

1~2倍max厚度下的结果如图5a、图6a、图6b所示，当水流流速为0.3 m/s时，颗粒组的平均速度为0.000 4 m/s，即1.44 m/h，此时，骨料运动速度很低，基本在原地不动。当水流速度增至0.6 m/s时，颗粒速度出现显著的平面分带性，前端高尾部低，颗粒组平均速度为0.145 m/s，即522 m/h，此时的水流流速可有效起动颗粒组。3~5倍max厚度下结果如图5b、图6c、图6d所示，当水流速度0.9 m/s时，骨料颗粒速度分布呈现空间分带性，暴露于流场迎水面及前端的颗粒速度较高，背水面及内部的速度较低，颗粒组的平均速度为0.003 m/s，即10.8 m/h，此时，骨料的运动速度对灌注过程不可忽略，水流可有效搬运颗粒组。据以往经验，为减少无效灌注，颗粒组的运动速度应小于1.5 m/h，即每天按16 h计算，运动距离小于钻孔间距25 m。

表1将3种颗粒组(5~10、10~30、30~50 mm)、2种厚度(1~2倍max和3~5倍max)下模拟的有效起动流速和前人实验拟合公式(16)[22]得出的数据进行对比，发现1~2倍max厚度下的颗粒进行起动时，起动流速靠近拟合值的下限，在3~5倍max厚度下的颗粒进行起动时，起动流速靠近拟合值的上限，实际施工中骨料厚度远大于1~2倍max，因而起动流速应取模拟和拟合值的上限。

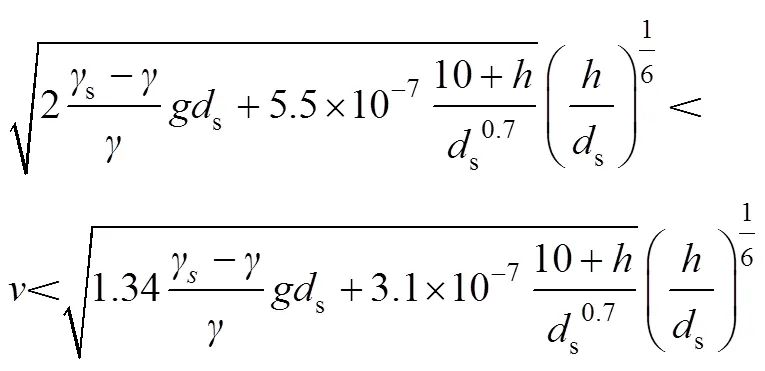
式中：v为实测的起动速度；γs、γ分别为颗粒及水的容重；ds为颗粒直径；h为未接顶高度。

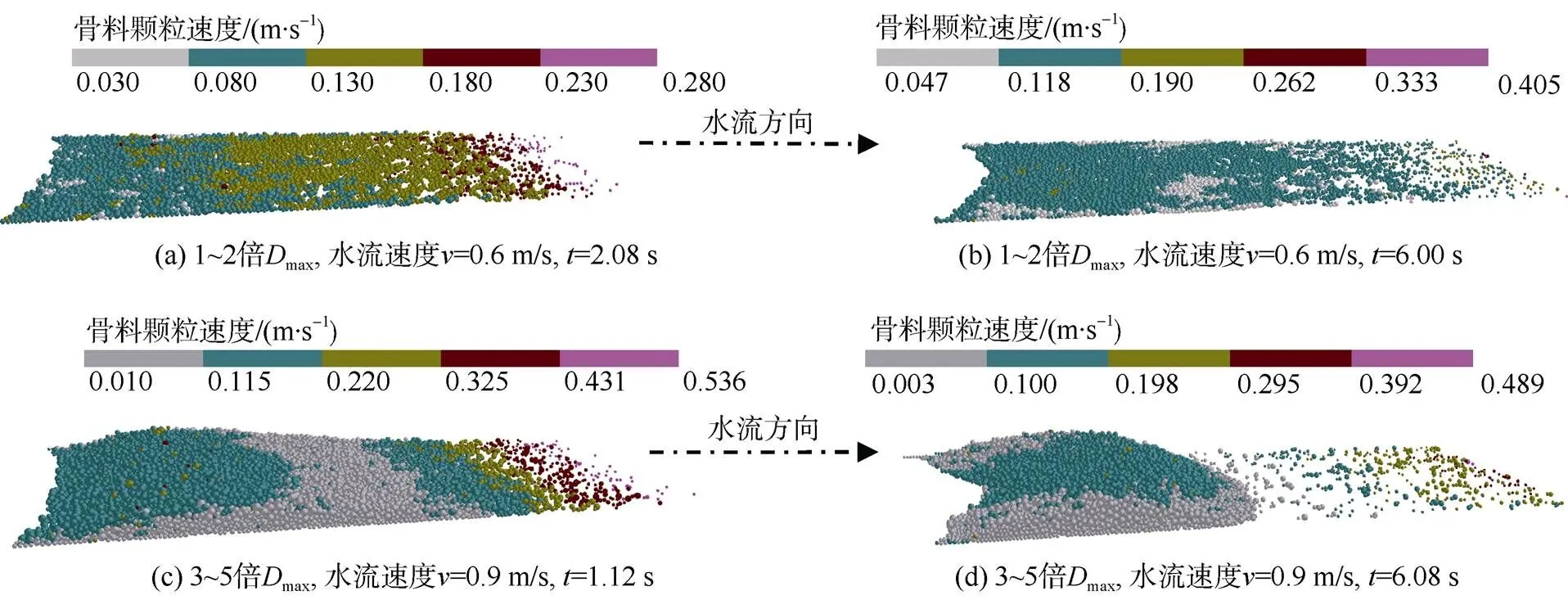
图6 不同堆积厚度的粒径5~10 mm颗粒在流场作用下的运动速度分布

表1 起动流速拟合值与模拟值对比

2.3 水流携砂能力和未接顶区流速放大率

计算模型采用长宽高分别为500、20、20 cm的模拟巷道，网格剖分采用2 cm的六面体，据现场经验推算20 cm巷宽时，单孔等效灌注速度为0.4 kg/s，下面以5~10 mm的骨料为例，模拟不同流速携带骨料的能力。

如图7所示，向巷道内持续灌注骨料并不断增加灌注速度，结果表明，特定流场携带骨料的能力存在上限。当灌注能力大于水流的携砂能力时，堆积高度将迅速增加，使流场等值线重新分布，未接顶区的流速不断增加；如果调整后的流场依然无法携带走当前灌注速度下的骨料，则堆积高度会持续增加直至达到新的平衡状态或接顶。当灌注速度小于流速携带能力时，堆积高度将无法持续增长。观察流场与堆积形态的位置关系，发现堆积区与未堆积区的过渡区对应的流场速度区间，正好与该粒组有效起动速度上限相吻合。

分别对各级骨料(5~10 mm、10~30 mm、30~50 mm)颗粒进行模拟，结果统计见表2。平均流速为关注初期巷道内的水流流速，其大小决定了骨料灌注过程中的总体流速区间，但决定携砂能力大小的关键因素为未接顶主流区所能达到的最大流速范围，这由初始流速和突水前水压共同决定。随着骨料灌注临近接顶，流量在断面空间上重新分布，已充填的细骨料可视为不过水断面，由于流量守恒未接顶区平均流速将增大至初始断面流速的数倍以上，现场初始平均流速一般为0~0.5 m/s，本次模拟直接采用较高初始流速1~2.5 m/s。

图7 水流的携砂能力测试及流速空间分布

表2 不同工况下水流携砂能力模拟统计结果

注：流速放大系数=顶区最大流速/平均流速，用于描述未接顶区流速的放大程度。

2.4 静水条件下的堆积形态

计算模型采用长宽高分别为1 000、20、20 cm的模拟巷道，网格剖分采用边长2 cm的六面体(下同)。如图8所示，静水环境下分别在水平、倾角15°的巷道中灌注骨料，发现倾斜巷道中靠下山相对于巷道底板的休止角与巷道倾角之和，刚好等于水平状态下的休止角；靠上山相对于巷道底板的休止角减去巷道倾角，也等于水平状态下的休止角。因此，巷道倾角只是改变堆积形态与坡脚的相对关系，并没有改变相对于水平线的休止角。随着巷道角度变大，同等条件下下山巷道中容易产生较长的拖尾。

图8 静水中骨料在倾斜(倾角15°)巷道、水平巷道中堆积试验对比

2.5 动水条件下的堆积形态

如图9—图11所示，分别在流速为0.5、0.7、0.9 m/s的条件下以相同的速度灌注骨料，测试骨料在下山15°、上山15°、水平巷道中堆积形态和起动速度的差异性。

如图9所示，对于30~50 mm的颗粒，经过测量发现在0.5~0.9 m/s的流速条件下，在下山、水平和上山巷道中，背水面的休止角除个别偏差较大外，总体上均在40°左右，主要原因是流速相对于颗粒粒径而言较低，堆积体倾角接近静水环境下的状态。如图10所示，对10~30 mm的颗粒情况开始发生变化，在较低速度0.5 m/s时，3种倾角巷道中骨料很快接顶，相对水平线堆积角接近静水休止角。当流速增加至0.7~0.9 m/s时，堆积角明显小于静水休止角。如图11所示，对于5~10 mm的颗粒也存在该现象，但由于颗粒粒径小，堆积角数值相对稳定。

2.6 倾角对起动流速的影响

结合图9—图11观察相同流速条件下的堆积高度，分析不同巷道倾角中水流携砂能力的差异性。所有工况均设置80%巷道高度为堆积上限，模拟未接顶前的情况。测试成果见表3，在平均流速相同的条件下，对于不同的巷道倾角，如果堆积高度越高，说明当前流速潜在携砂能力越弱，即流速进一步增加的空间越低。

模拟结果显示，在0.5~0.9 m/s流速下，30~50 mm粒组均无法被水流有效搬运导致接顶。由于该粒组在水平巷道中的有效起动速度在1.6 m/s以上(表1，取上限，下同)，且该粒组颗粒直径大，阻水消压能力弱，在未接顶区对流速的放大系数太低(表2，放大率最大1.3，下同)，导致即使在下山巷道中，对起动速度进行折减后(折减系数如图4所示，下同)仍无法有效起动该粒组，0.9×1.3=1.17 m/s＜1.6×0.77=1.23 m/s。

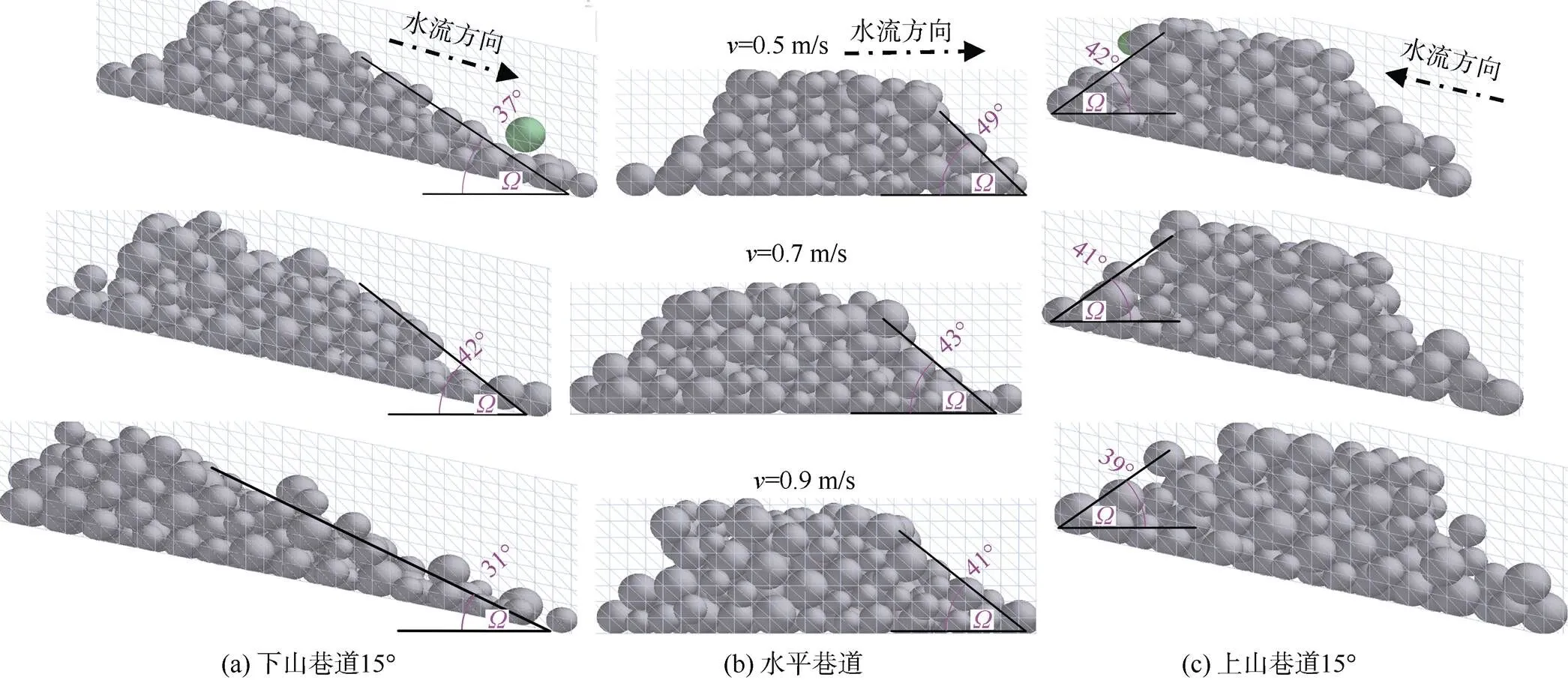
图9 粒径30~50 mm颗粒在不同流速下倾斜(±15°)及水平巷道中堆积试验对比

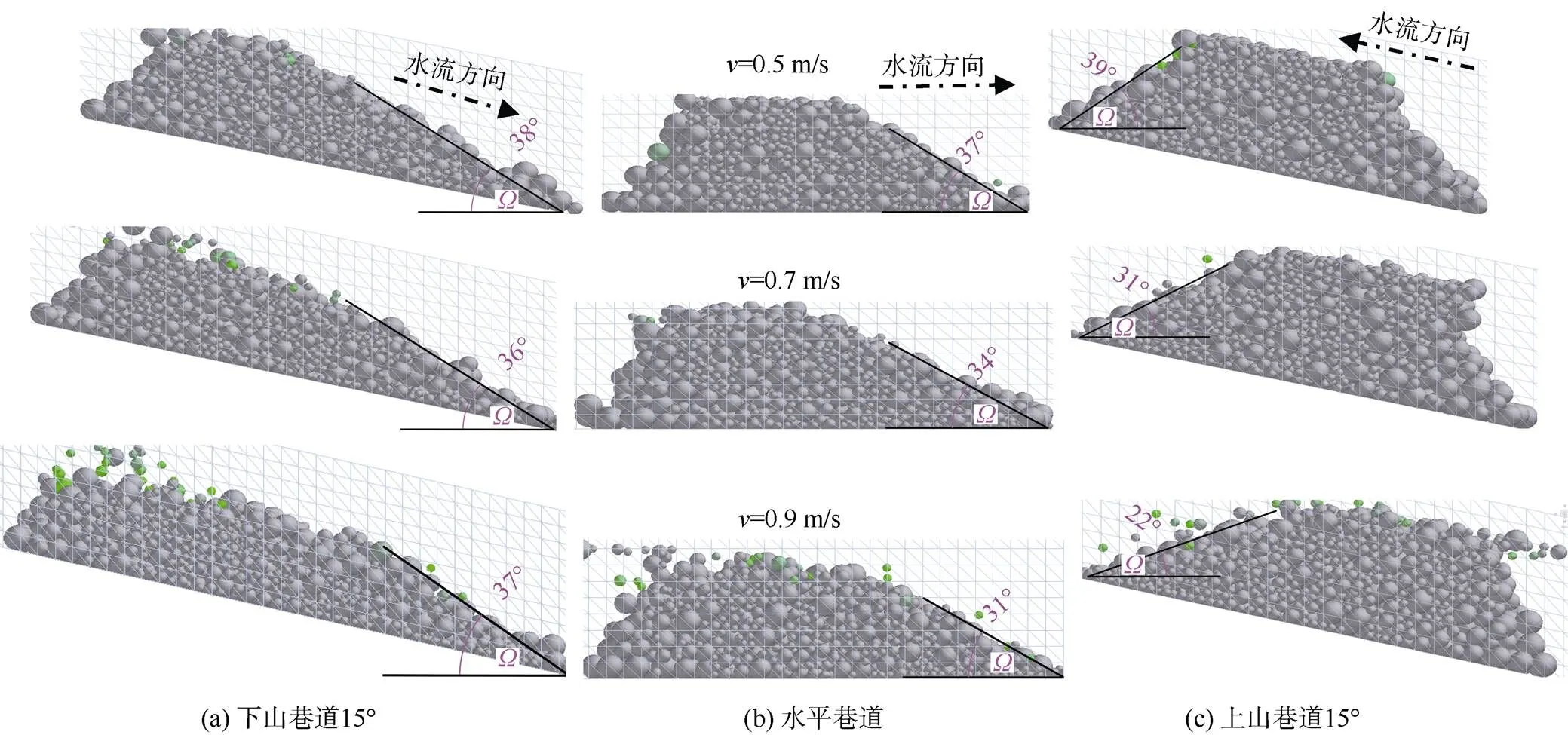
图10 粒径10~30 mm颗粒在不同流速下倾斜(±15°)及水平巷道中堆积试验对比

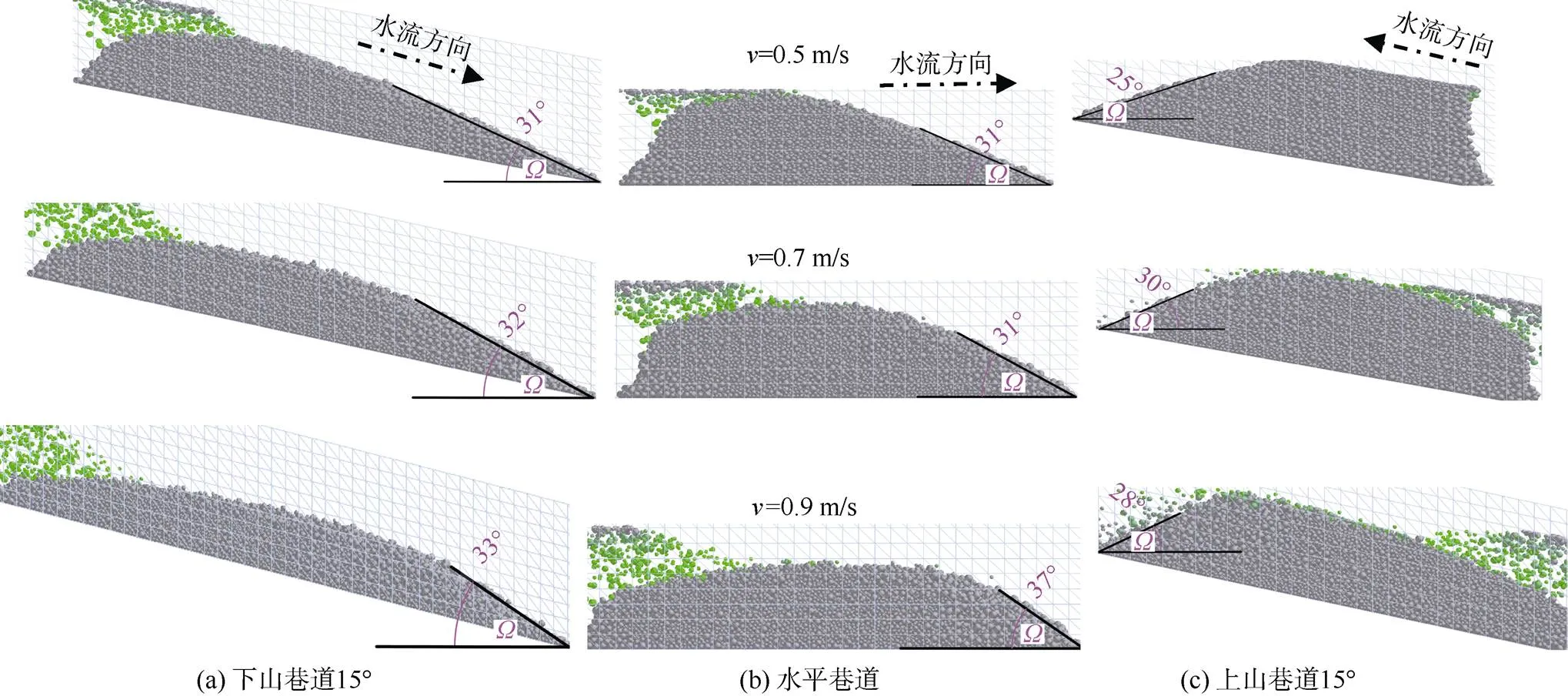
图11 粒径5~10 mm颗粒在不同流速下倾斜(±15°)、水平巷道中堆积试验对比

对于10~30 mm颗粒，水平巷道中有效起动速度1.3 m/s以上，下山巷道中按0.77折减，有效起动速度应大于1.0 m/s，当平均流速达到0.7、0.9 m/s时，按最大约2倍放大系数，顶部加速区流速可达1.4~1.8 m/s，已可以有效起动该颗粒组。对于上山巷道，起动速度按1.16倍进行增加，起动速度应大于1.5 m/s，当巷道平均流速0.9 m/s时，按最大约2倍放大系数，顶部流速可达到1.8 m/s，可以起动颗粒。对于水平巷道，堆积设置80%高度，平均速度0.7 m/s时，顶部加速区达不到1.3 m/s的流速，导致接顶，当平均流速0.9 m/s时，堆积高度达到75%时可以起动。

对于5~10 mm颗粒组，水平巷道中有效起动速度0.9 m/s以上，顶部最大约2.6倍的流速放大系数，流速0.7 m/s时顶部放大2.6倍后达到1.82 m/s，可有效起动(0.5 m/s流速受堆积高度80%限制，颗粒受阻无法起动)。对于下山，起动速度按0.77进行折减，有效起动速度应大于0.7 m/s，平均流速0.5 m/s时放大2.6倍后达到1.3 m/s，可起动。对于上山，起动速度按1.16进行增加，有效起动速度应大于1.0 m/s以上，平均流速0.7 m/s时放大2.6倍达到1.82 m/s，可起动颗粒。

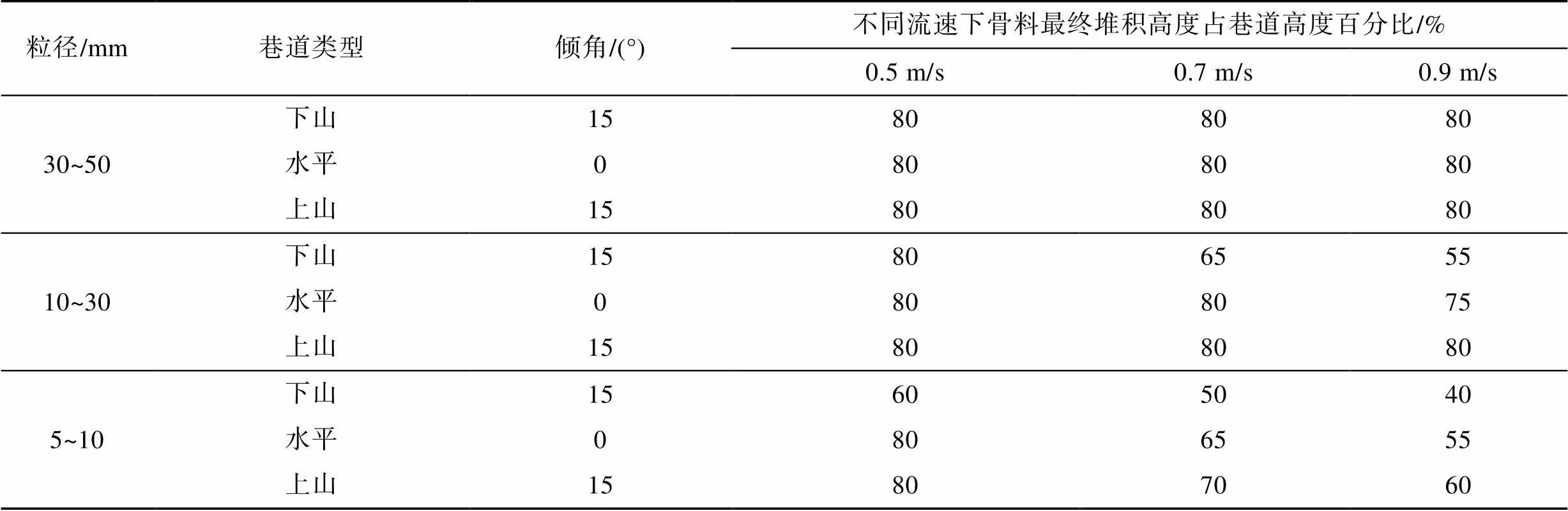
表3 不同倾角巷道中骨料堆积高度测试结果对比

以上分析进一步证明骨料颗粒的有效起动速度与巷道倾角的密切关系，也验证第1节中起动模型的正确性。在倾斜巷道中投注骨料时，应根据上山或下山及流速条件，对起动流速进行适当的折减或增加，并在此基础上做出骨料粒径选择。巷道倾角的存在，相同水流的携砂能力随倾角的增加或减小而发生密切变化，对实际工程会产生重要影响，表现为：

①同等涌水量(流速)条件下，其他灌注条件相同时，堆积高度由大到小依次为：上山、水平、下山，上山位置进行骨料灌注更容易接顶，率先达到截流条件，缩短施工周期。

②同等条件下在下山中灌注时，起动速度最低，堆积体向巷顶方向生长相对困难，向巷道长轴方向生长相对容易，这降低了截流成功的概率，因此，在允许条件下阻水墙选址应尽量设置在水平或上山巷道。

3 结论

a.建立了动水环境中倾斜巷道颗粒起动的临界判据，上山巷道起动速度相对水平巷道有所增加，下山巷道则相应折减，3种倾角巷道中颗粒起动速度的平方之比值为：(tancos+sin)︰tan︰(tancos–sin)。

b. 5~10 mm、10~30 mm、30~50 mm颗粒组在1~2倍max和3~5倍max2种堆积厚度下起动速度的测试结果线上，其分别靠近拟合值的下限和上限，灌注过程中起动速度取靠近拟合值上限时具有实际工程意义。水流的携砂能力测试发现，未接顶区和堆积区的过渡区对应起动流速上限。当流场携砂能力小于骨料灌注能力时，表现为接顶相对容易，否则接顶困难。

c. 静水环境下5~10 mm、10~30 mm、30~50 mm颗粒组在巷道中的堆积角模拟发现，巷道倾角对堆积体相对于水平线的堆积角没有影响。在0.5、0.7、0.9 m/s的动水条件下，堆积体在下山巷道中形态被“拉长”不易接顶，上山巷道中被“压缩”容易接顶。

d.骨料灌注过程中应根据当前流速和巷道倾角条件选取正确的骨料灌注参数，包括灌注速度、灌注粒径及灌注次序，以满足骨料堆积长度和高度同步“生长”，达到截流阻水的要求。

[1] 王威. 动水条件下堵巷截流技术与阻水段阻水能力研究[D]. 北京：煤炭科学研究总院，2012.WANG Wei. A study on techniques of roadway-blocking & flow-cutting off under hydrodynamic conditions and capability evaluation of water-blocking segment[M]. Beijing：Coal Science Research Institute，2012.

[2] 开滦矿务局，煤科院地质勘探分院，煤科院建井研究所. 开滦范各庄矿岩溶陷落柱特大突水灾害的治理[J]. 煤田地质与勘探，1986，12(2)：35–42.Kailuan Mineral Board，Geological Exploration Branch of Coal Research Institute，Mine Construction Branch of Coal Research Institute. Treatment of the great water inrush in karst collapse column in Fangezhuang mine[J]. Coal Geology & Exploration，1986，12(2)：35–42.

[3] 王则才. 国家庄煤矿8101工作面动水注浆堵水技术[J]. 煤田地质与勘探，2004，32(4)：26–28.WANG Zecai. Grouting technique for water-shut-off under water-flowing conditions in No.8101 work-face，Guojiazhuang coal mine[J]. Coal Geology & Exploration，2004，32(4)：26–28.

[4] 刘建功，赵庆彪，白忠胜，等. 东庞矿陷落柱特大突水灾害快速治理[J]. 煤炭科学技术，2005，33(5)：4–7.LIU Jiangong，ZHAO Qingbiao，BAI Zhongsheng，et al. Rapid holding and control for special large water inrush from sink hole in Dongpang mine[J]. Coal Science and Technology，2005，33(5)：4–7.

[5] 南生辉. 综合注浆法建造阻水墙技术[J]. 煤炭工程，2010，42(6)：29–31.NAN Shenghui. Construction technology of water blocking wall by comprehensive grouting method[J]. Coal Engineering，2010，42(6)：29–31.

[6] 邵红旗，王维. 双液注浆法快速建造阻水墙封堵突水巷道[J]. 煤矿安全，2011，42(11)：40–43.SHAO Hongqi，WANG Wei. Fast construction of water blocking wall by double liquid grouting[J]. Safety in Coal Mines，2011，42(11)：40–43.

[7] 岳卫振. 平衡压力法在极松散煤巷注浆截流堵水中的应用[J]. 煤炭工程，2012，44(8)：40–42.YUE Weizhen. Balanced pressure method applied to grouting and water sealing of loose seam gateway[J]. Coal Engineering，2012，44(8)：40–42.

[8] 姬中奎. 矿井特大突水巷道动水截流钻探技术研究[J]. 煤炭技术，2014，33(5)：12–14.JI Zhongkui. Research on drilling technology for roadway dynamic water sealing in supergiant water inrush coal mine[J]. Coal Technology，2014，33(5)：12–14.

[9] 李维欣. 圆型过水巷道骨料灌注模拟试验[D]. 徐州：中国矿业大学，2016.LI Weixin. An experimental simulation on aggregate filling to horizontal circular tunnel with flowing water[D]. Xuzhou：China University of Mining and Technology，2016.

[10] 惠爽. 矿井淹没巷道多孔灌注骨料封堵模拟试验[D]. 北京：中国矿业大学(北京)，2018.HUI Shuang. An experimental investigation on pouring aggregate to plug an inundated mine tunnel through boreholes[D]. Beijing：China University of Mining and Technology(Beijing)，2018.

[11] SHAMY U EI，ASCE S M，ZEGHAL M，et al. Coupled continuum-discrete model for saturated granular soils[J]. Journal of Engineering Mechanics，2005，131(4)：413–426.

[12] 周健，周凯敏，姚志雄，等. 砂土管涌–滤层防治的离散元数值模拟[J]. 水利学报，2010，41(1)：17–24. ZHOU Jian，ZHOU Kaimin，YAO Zhixiong，et al. Numerical simulation of piping-filter prevention in sandy soil by discrete element method[J]. Shuili Xuebao，2010，41(1)：17–24.

[13] ZHOU Jian，LI Yexun，JIA Mincai，et al. Numerical simulation of failure behavior of granular debris flows based on flume model tests[J]. The Scientific World Journal，2013：1–10.

[14] 罗勇，龚晓南，吴瑞潜. 颗粒流模拟和流体与颗粒相互作用分析[J]. 浙江大学学报(工学版)，2007，41(11)：1932–1936. LUO Yong，GONG Xiaonan，WU Ruiqian. Analysis and simulation of fluid-particles interaction with particle flow code[J]. Journal of Zhejiang University(Engineering Science)，2007，41(11)：1932–1936.

[15] 王胤，艾军，杨庆. 考虑粒间滚动阻力的CFD-DEM流–固耦合数值模拟方法[J]. 岩土力学，2017，38(6)：1771–1780.WANG Yin，AI Jun，YANG Qing. A CFD-DEM coupled method incorporating soil inter-particle rolling resistance[J]. Rock and Soil Mechanics，2017，38(6)：1771–1780.

[16] 蒋明镜，张望城. 一种考虑流体状态方程的土体CFD-DEM耦合数值方法[J]. 岩土工程学报，2014，36(5)：793–801.JIANG Mingjing，ZHANG Wangcheng. Coupled CFD-DEM method for soils incorporating equation of state for liquid[J]. Chinese Journal of Geotechnical Engineering，2014，36(5)：793–801.

[17] 景路，郭颂怡，赵涛. 基于流体动力学–离散单元耦合算法的海底滑坡动力学分析[J]. 岩土力学，2019，40(1)：388–394.JING Lu，GUO Songyi，ZHAO Tao. Understanding dynamics of submarine landslide with coupled CFD-DEM[J]. Rock and Soil Mechanics，2019，40(1)：388–394.

[18] 刘卡，高辰龙，周玉. 基于CFD-DEM方法的水下抛石运动模拟研究[J]. 中国水运：航道科技，2016(6)：1–9.LIU Ka，GAO Chenlong，ZHOU Yu. Simulation of underwater riprap motion based on CFD-DEM method[J]. China Water Transport：Channel Technology，2016(6)：1–9.

[19] 苏东升. 基于CFD-DEM耦合模拟方法的水流泥沙运动研究[D]. 天津：天津大学，2016.SU Dongsheng. Investigation of fluid-sediment particle motion based on CFD-DEM coupling simulation method[D]. Tianjin：Tianjin University，2016.

[20] 邵兵，闫怡飞，毕朝峰，等. 基于CFD-DEM耦合模型的大粒径非常规岩屑颗粒运移规律研究[J]. 科学技术与工程，2017，17(27)：190–195.SHAO Bing，YAN Yifei，BI Chaofeng，et al. Migration of irregular cuttings particles in big size by CFD-DEM coupled simulation model[J]. Science Technology and Engineering，2017，17(27)：190–195.

[21] 黄文博，李潭秋，杨润泽，等. 基于CFD-DEM的颗粒填充床压力下降仿真和实验验证[J]. 航天医学与医学工程，2018，31(5)：526–531.HUANG Wenbo，LI Tanqiu，YANG Runze，et al. Simulation and experimental validation of pressure drop in packed bed based on CFD-DEM[J]. Space Medicine & Medical Engineering，2018，31(5)：526–531.

[22] 何文社，方铎，杨具瑞. 泥沙起动流速研究[J]. 水利学报，2002，33(10)：51–56.HE Wenshe，FANG Duo，YANG Jurui. Study on incipient velocity of sediment[J]. Shuili Xuebao，2002，33(10)：51–56.

Mechanism of aggregate start-up process and coupling of two-phase flow in hydrodynamic roadway

MOU Lin1,2

(1. China Coal Research Institute, Beijing 100013, China; 2.Xi’an Research Institute Co. Ltd., China Coal Technology and Engineering Group Corp., Xi’an 710077, China)

In order to study the relationship between the aggregate accumulation state in the roadways with hydrodynamic water and the inclination angle of the roadways, the criterion for the start of aggregate particles in the inclined roadways were established. A numerical mechanics model(CFD-eDEM) describing the process of aggregate infusion was established using computational fluid dynamics and discrete element method, the start-up velocity and water carrying capacity of 5-10 mm, 10-30 mm and 30-50 mm aggregate particle groups under different accumulation thickness were tested, and the static water accumulation angle and dynamic water accumulation shape of each particle group in different inclined roadways were simulated. The results are as follows: The starting speed decreases in order of ascending roadway, horizontal roadway and descending roadway, and the ratio of the square of starting speed was (tancos+sin): tan: (tancos–sin). It was found that the shape of the accumulation is determined by the dynamic equilibrium state of the flow field and the pouring capacity. When the carrying capacity of the flow field is much smaller than the pouring capacity, it is easy for the accumulatiom to connect the top, and vice versa. It shows that the inclination angle of the roadway has no effect on the accumulation angle. Under the same flow velocity, the accumulation form of aggregate in the downhill roadway is “stretched” and not easy to connect to the top, while it is “compressed” in the uphill roadway and relatively easy to connect to the top. During the construction process, the uphill section should be selected as much as possible to reduce the construction difficulty. After the site of the project is determined, the particle size in the downhill should be appropriately increased, and reduced correspondingly in the uphill, so as to achieve rapid closure and reduce ineffective perfusion engineering.

CFD-DEM; filling aggregate;hydrodynamic roadway; water cut-off; solid-liquid two-phase

请听作者语音介绍创新技术成果等信息，欢迎与作者进行交流

TD741

A

10.3969/j.issn.1001-1986.2020.06.022

1001-1986(2020)06-0161-09

2020-08-04；

2020-10-13

国家重点研发计划开发项目(2017YFC0804100)；中煤科工集团西安研究院有限公司科技创新基金(2019XAYMS22)

National Key R & D Projects(2017YFC0804100)；Science and Technology Innovation Fund of CCTEGXIAN(2019XAYMS22)

牟林，1985年生，男，湖北松滋人，博士研究生，副研究员，从事煤矿水害防治方向研究．E-mail：258323938@qq.com

牟林.过水巷道中骨料起动力学机制及两相流耦合模拟[J]. 煤田地质与勘探，2020，48(6)：161–169.

MOU Lin. Mechanism of aggregate start-up process and coupling of two-phase flow in hydrodynamic roadway[J]. Coal Geology & Exploration，2020，48(6)：161–169.

(责任编辑 周建军)