基于权重熵的碾压混凝土坝温度场预警方法

牛景太，杨 光,雷 鹏

(1.南昌工程学院 水利与生态工程学院，江西 南昌 330099；2.华北水利水电大学 水利学院，河南 郑州 450046;3.长沙理工大学 水利工程学院，湖南 长沙 410114)

1 研究背景

目前，我国的碾压混凝土坝建设已达到国际领先水平，碾压混凝土坝是我国坝工发展最有前景的坝型之一[1]。碾压混凝土坝因采用薄层浇筑、连续上升的施工方式，坝体最高温度出现的相对较晚，降温过程也相对更为缓慢，因此，碾压混凝土坝温度变化规律与常态混凝土坝有一定的相似性，但又具有自身的特点[2]。此外，由于层面的温度线膨胀系数有别于本体，自由膨胀在竖向和横向的表现自然也不相同，本体和层面间也会产生接触附加应力。因此，有必要深入研究碾压混凝土坝温度变化规律，据此制定科学合理的混凝土大坝温度预警准则[3-6]。目前，已有部分学者对大坝温度监控指标进行了研究[7-11]，现有成果多局限于研究温度场整体性态和点温度的预警方法，缺少对整体温度场的相关探讨，实际上，针对点温度的预警方法已无法满足工程实际，碾压混凝土坝的温度场变化性态研究亟需从点扩展至空间整体。因此，研究能合理表达碾压混凝土坝空间温度场的方法，并提出碾压混凝土坝整体温度场预警方法，具有重要意义。

综合运用信息熵、协同学理论，分析大坝温度场与点温度之间的关系，将温度场视为不同贡献度的单测点相互作用、相互影响的一个系统，据此构建权重熵表达式，综合评价碾压混凝土坝温度场整体变化性态，在此基础上，应用小概率法原理，建立碾压混凝土坝温度场预警准则，依据实际工程，对本文所提出的方法进行验证和检验。

2 预警指标

熵是用来表示系统的一个状态函数[12-13]，其表达式为：

(1)

式中：dS为状态函数熵的微分；δQ为系统与环境交换的热量；下标rev表示过程是可逆的;T为热源的温度。所以，熵是系统的状态函数。

熵的物理意义为：

S=klnΩ

(2)

式中：k为波尔兹曼常数；Ω为微观量子态数目，即宏观态出现的概率。

根据玻尔兹曼的定义，熵是系统无序程度的一个度量。在实际应用中，可以通过计算碾压混凝土坝各个测点温度测量值的有序度来计算各测点的权重熵，从而确定碾压混凝土坝空间温度场的温度预警指标。

根据协同学的相关原理[14]，将碾压混凝土坝温度场视为不同贡献度特征点相互作用、相互影响的一个综合体，其结构体系如图1所示。通过研究单点对整体的贡献程度，构建碾压混凝土坝温度场权重熵的表达式。

图1 碾压混凝土坝温度场结构体系

(1)单测点温度的熵。测点i的第j个温度测值的有序度μij定义如下：

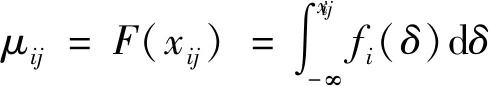
(3)

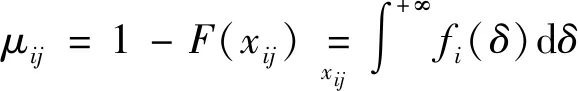
(4)

式中：fi(δ)为测点i的概率密度函数；F(x)为概率分布函数。

由公式(3)和公式(4)可知，碾压混凝土坝温度监测值偏离初始状态越大，则μij越大；温度监测值愈接近初始状态，则μij越小。从信息熵的定义出发，令xij为温度测值，其熵sij可定义为[16]：

sij=-[μijlnμij+(1-μij)ln (1-μij)]

(5)

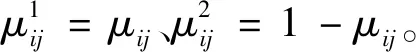
(2)温度场权重熵。在公式(5)的基础上，温度场权重熵Sj可定义为：

(6)

将公式(6)分解，可得：

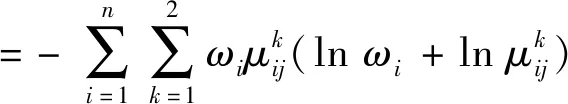
(7)

(3)权重计算。本文利用投影寻踪法(projection pursuit analysis，简称PPA)[14-19]，将高维数据投影到低维子空间，计算权重ωi。假设n测点的权重分布为{ωi|i=1,2,…,n}，则ωi满足：ωi≥0，∑ωi=1。计算ωi的步骤如下：

Step 1：构建矩阵D，可表示为：

(8)

式中：Dij=1-Sij。采用下式进行极值归一化处理：

(9)

式中：[Dj]max、[Dj]min分别为矩阵D第j列的最大值和最小值。

(10)

Step 3：构建投影目标函数。在约束条件下求解投影目标函数最大化问题，以此来估计最佳投影方向，即：

目标函数：max:H(p)=SG·QG

(11)

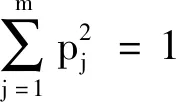
(12)

(13)

(14)

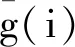
Step 4：求解出最佳投影方向P*，可计算权重值ωi，即：

(15)

3 预警准则

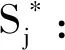
(16)

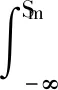
(17)

S分布求出后，确定失效概率Pα(简称α)。根据概率α和f(x)，权重熵预警指标即可被确定如下：

(18)

依据某工程的实际情况，根据不同的险情，由大至小设置若干个置信度α值：α1>α2>…>αn。算法计算流程见图2所示。

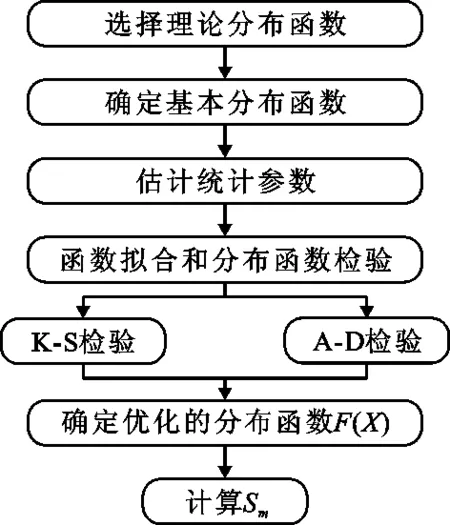
图2 预警指标计算流程图

4 实例计算与分析

4.1 工程概况

某水利枢纽主要由碾压混凝土重力坝、溢流表孔、泄槽及消力池、右岸泄洪(冲沙)底孔、左岸冲沙底孔、坝后厂房及进厂交通洞等永久建筑物及导流隧洞、围堰等临时建筑物组成。坝顶高程1 424 m，最大坝高160 m，坝顶长度640 m，以该工程6#坝段为例，验证本文所提出的方法。6#坝段温度测点布置见图3。

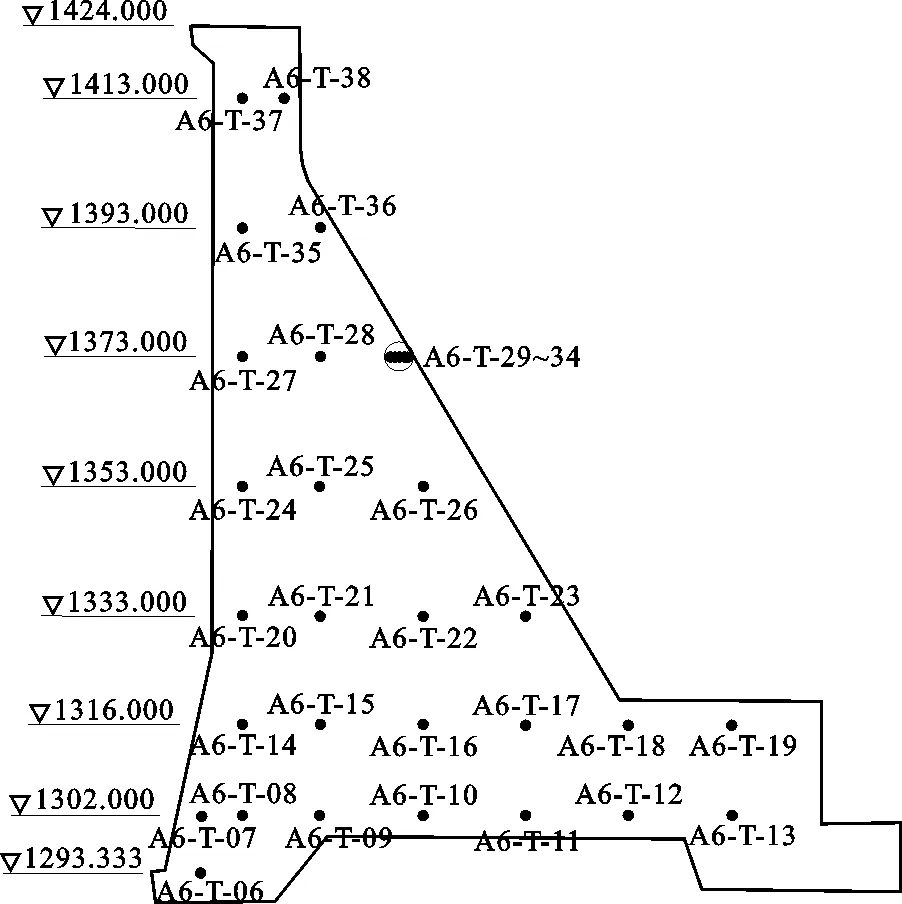
图3 实例工程6#坝段横断面温度测点布置图

本文选取2007年8月1日至2014年1月20日温度监测资料作为样本进行分析，选定6#坝段A6-T-06～ A6-T-38共33个测点的温度监测资料计算权重熵及其预警值。

4.2 温度场变化规律分析

大坝坝体混凝土施工期温度主要由混凝土水化热引起，而运行期混凝土自身热量已基本释放完毕，混凝土温度主要受库水温和气温的影响，一般呈周期性变化，因此，为了区分坝体混凝土温度不同时期影响因素的不同，将监测资料时间序列分为4个阶段：浇筑至高程1 311.0 m(2007-08-01至2008-03-06)、浇筑至高程1 360.0 m(2008-03-07至2008-08-10)、浇筑至高程1 422.5 m(2008-08-11至2009-11-26)以及大坝运行4 a末(竣工至2014-01-20)。

本文在采用 PPA 投影追踪法计算各测点权重时，分别计算了各测点在4个不同阶段的权重分布值，其计算结果如图4所示。为了验证权重分布值的合理性，特针对4个阶段采用MSC.MARC分析平台进行温度场计算，可以明显看出温度应力较高的部位对应的权重值较大，符合实际工程情况。图5为6#坝段在研究时段4个阶段末的坝体温度分布，图6为研究时段内6#坝段温度场权重熵的过程线。

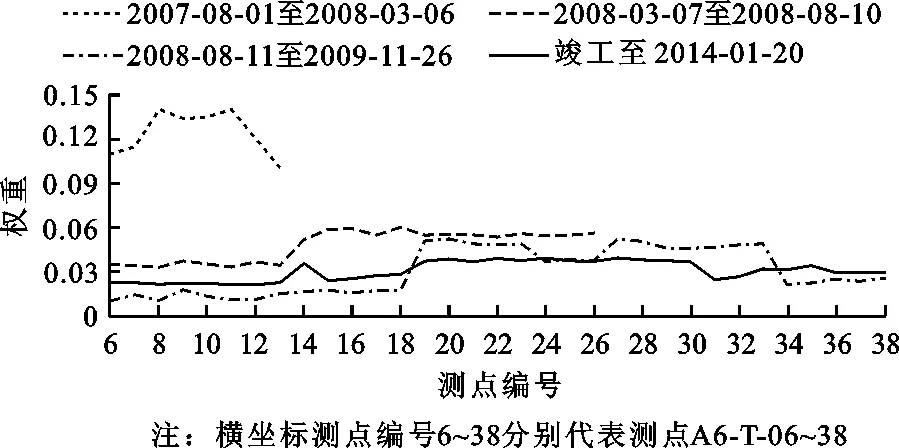
图4 实例工程6#坝段在研究时段4个阶段各温度测点权重分布

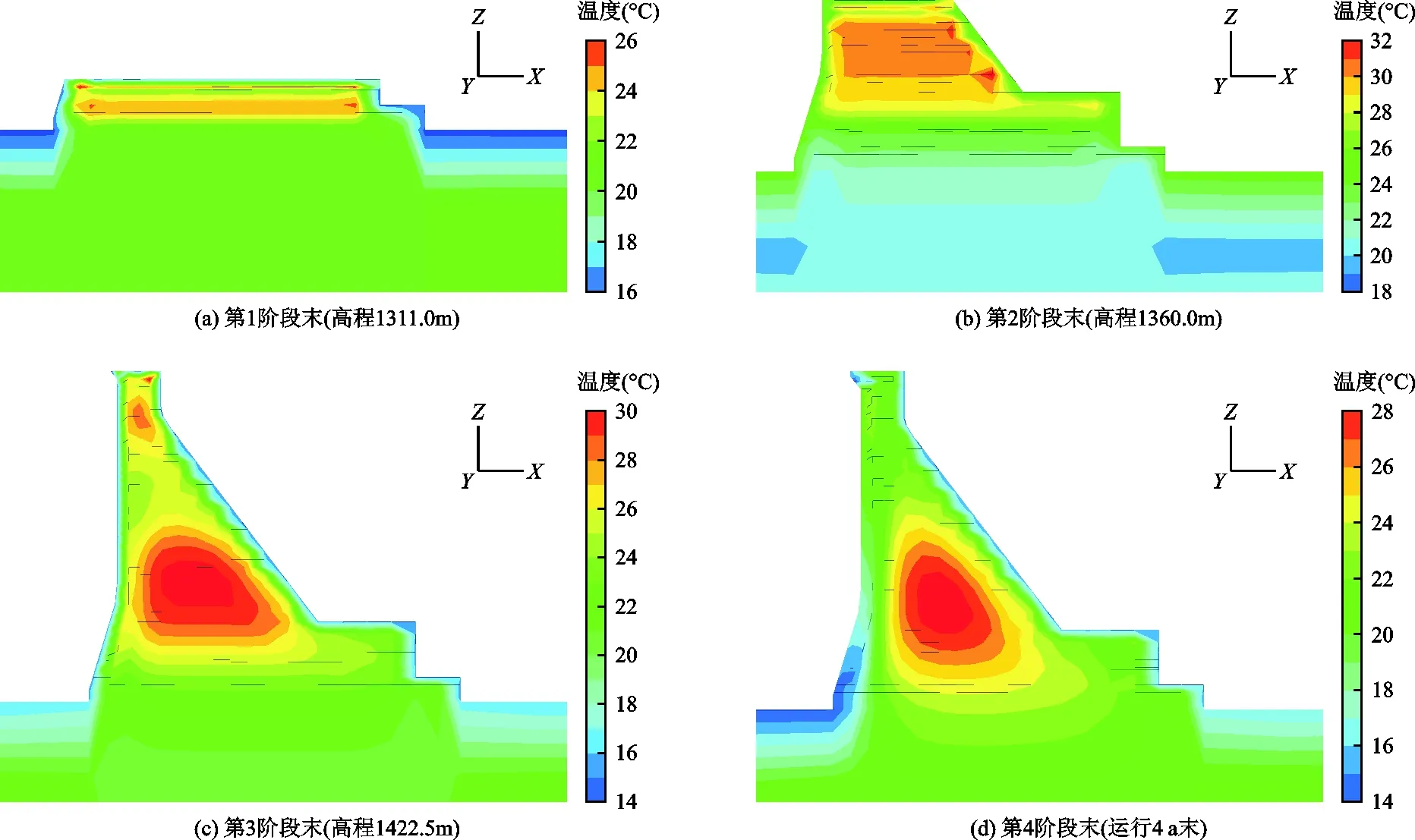
图5 实例工程6#坝段在研究时段4个阶段末的坝体温度分布

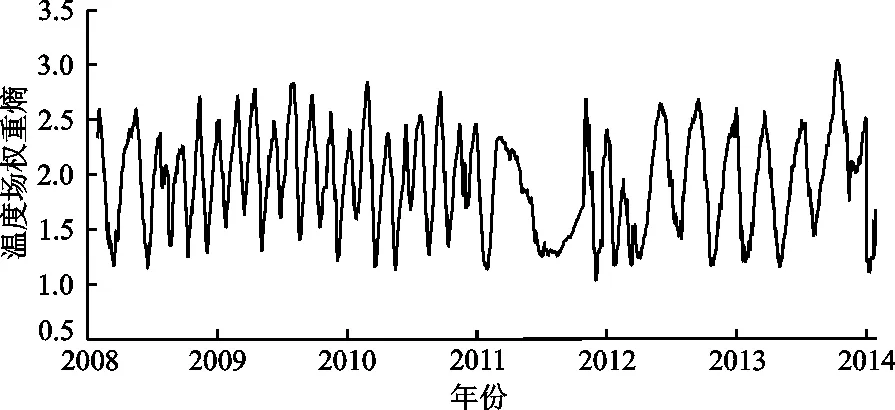
图6 研究时段内实例工程6#坝段温度场权重熵过程线

现根据上述成果，结合6#坝段典型测点(A6-T-21测点)温度监测值时间序列(图7)及该工程环境气温过程线(图8)对坝体温度场权重熵的变化规律进行分析。由图6 ～8可知：(1)施工期温度场权重熵受混凝土自身水化热影响非常显著。施工期每个阶段前期，坝体温度场权重熵逐渐减小，这是因为混凝土初期释放了巨大热量，导致坝体温度急剧上升。而由于排水管降温和自身散热作用，坝体混凝土温度随之逐渐下降，此时权重熵又逐渐增大。总体来看，施工阶段权重熵过程线波动频繁，权重熵多次出现最小值(图6)，表明混凝土浇筑过程中坝体温度多次出现波峰，这与实际坝体温度变化规律一致；(2)自第3阶段结束后，大坝进入正常的运行期，坝体温度主要受气温等环境因素影响，坝体温度开始逐渐下降并趋于平稳，而且由于环境因素的影响表现出周期性变化(图7)，此时的权重熵计算值也呈现周期性波动，显然与测点实测温度过程线的变化规律一致。

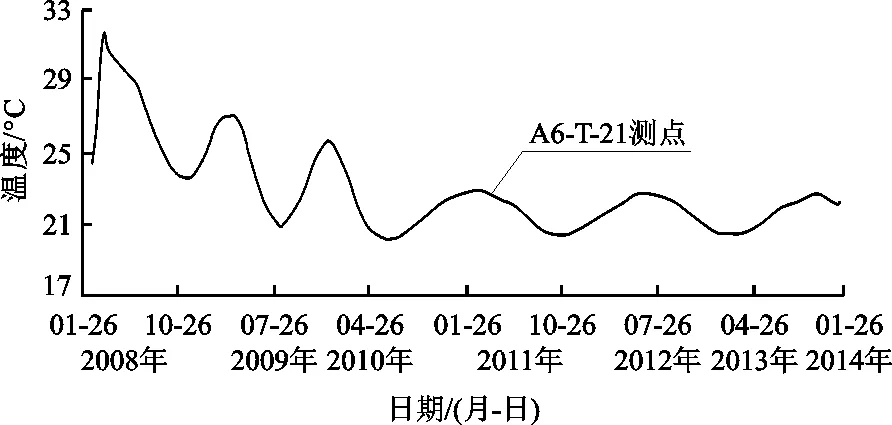
图7 实例工程研究时段6#坝段典型温度测点监测值时间序列

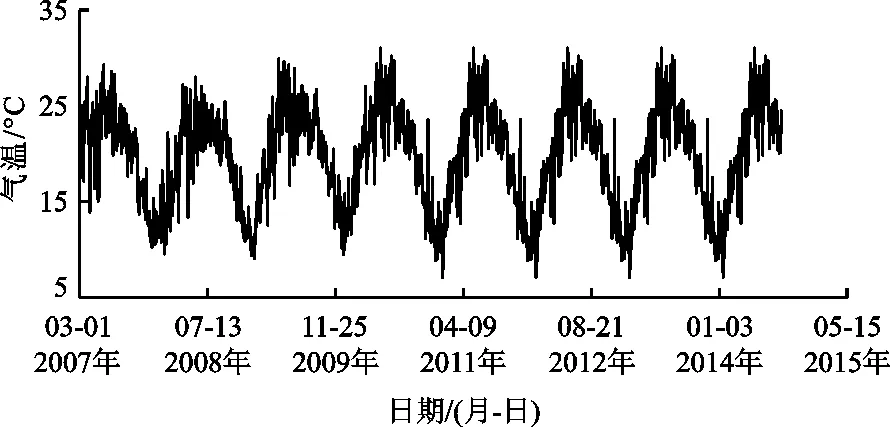
图8 实例工程研究时段环境气温过程线

综上所述，本文结合不同阶段坝体温度主要影响因素，综合考虑坝体所有测点的贡献度，根据温度场协同有序演变的特点，构建的权重熵计算公式可以准确地反映坝体温度变化规律，而且与工程实际情况吻合。

4.3 预警指标拟定

选取6#坝段权重熵的极值，基于小概率法采用自编的MATLAB程序计算权重熵预警指标，研究时段内各年份权重熵的年最小值见表1。

表1 研究时段内各年份6#坝段温度场权重熵最小值统计表

经K-S检验，最小值的最优分布均为正态分布，其均值和标准差分别为1.14和0.0589，考虑到该工程坝体较高、施工层面大，一旦坝体温度变化剧烈将不可避免地产生裂缝。因此，预警等级设置为两个，即一级预警(α=5%)和二级预警(α=1%)，分别用于甄别、处理早期碾压混凝土坝坝体温度变化，以及发现坝体温度骤变从而进行紧急控温，计算结果见表 2。根据表1、2和图6～8，可判别和预警大坝整体温度场性态。

表2 坝体温度场权重熵预警值

5 结 论

现有碾压混凝土坝温度场预警多是基于单个测点进行分析，针对这一不足，从结构有序演变的角度出发,构建了碾压混凝土坝温度熵表达式，提出了针对碾压混凝土坝多测点综合信息进行温度预警的方法。

(1)基于概率法定义了温度监测值的有序度和无序度，利用投影追踪法研究了各空间测点的权重分布；根据温度场协同有序演变的特点，应用各测点的有序度序列值和权重分布值，构建了能描述碾压混凝土坝温度场有序性的权重熵。

(2)在上述研究的基础上，应用典型小概率原理，提出了碾压混凝土坝温度场预警准则。基于本文的研究成果，分析了某碾压混凝土坝单个坝段的整体温度场，结果表明，温度场有序性的权重熵与环境量及温度实测值的变化规律一致，验证了所提出方法的有效性。