基于渗流-管流耦合模型的辐射井取水效果影响因素分析

高文冰，夏 岩，喻晓琳，郭 路,胡海洋

(1.中国石油长庆油田分公司勘探开发研究院，陕西 西安 710054;2.低渗透油气田勘探开发国家工程实验室，陕西 西安 710054;3.长安大学 水利与环境学院，陕西 西安 710054)

1 研究背景

辐射井的结构较为复杂，主要由竖井和辐射管组成[1]。竖井一般位于河岸，而辐射管设置于地面以下一定深度，延伸到河床下部的含水层中，并与竖井连通，这样就能够将河水转化为相对纯净的地下水。目前，辐射井已广泛应用于水源地取水[2]、大坝防渗[3]、尾矿库降排水[4]、求取水文地质参数[5-6]、治理黄土高原滑坡[7]等方面。

起初辐射井等非管井的计算模型大多是根据线汇理论推导出来的，通过等强度分布的线汇方式对井管进行刻画[8-13]。此后，陈崇希等[14]总结了线汇理论刻画辐射井所存在的缺陷，并采用等效渗透系数的概念，对辐射井进行了重新定义，给出了新的辐射井计算模型。Wang等[15]在“渗流管流”耦合模型和“等效渗透系数”等理论的基础上，结合MODFLOW软件，不再用等效渗透系数刻画含水层中的井管，而是将其概化成由一系列相互连接的节点和管道组成的离散管网，并对黄河某水源地的允许开采量进行了计算。此后，众多学者纷纷采用这种方法对不同水源地的允许开采量进行了计算[16-19]。

然而，上述大多数学者的研究主要集中在计算模型和取水量上，对于影响辐射井取水量的因素研究较少。因此在辐射井建成后由于缺乏理论的指导，往往出现取水效率低，取水成本较高等问题。潘治霖[20]通过大型砂槽物理实验讨论了辐射管仰角、辐射管埋深及河流渗漏补给能力对辐射井取水效果的影响。然而，由于实验条件过于理想化，辐射井的取水机理在实际条件下可能并不适用。

因此，本文通过大型砂槽物理实验，对辐射井计算模型进行验证，并将验证后的模型应用于陕西省志丹县洛河金鼎水源地，模拟不同井结构条件下辐射井取水量的变化，揭示了相对复杂条件下辐射井的取水机理，这对辐射井的实际施工具有重要的指导意义。

2 物理实验装置与方法

通过大型砂槽物理实验对辐射井取水模型进行验证，将验证后的模型应用于洛河金鼎水源地，根据不同的影响因素，建立不同的数值模型，用逐步优选的方法，确定出辐射井的最优结构，并对影响因素进行分析。

2.1 砂槽物理实验装置

砂槽实验装置示意图及辐射井缩微模型如图1所示。实验所用的砂槽长363 cm，宽50 cm，高117 cm，坐标原点选在其平面图的左下角(图1(a))。砂槽由5 mm厚的钢板制成，在砂槽的前后两个侧壁共有180个(18列×10层)测压观测孔，它们伸入砂槽的长度不同，以观测不同位置的水头变化。流量采用三角堰和量筒测量。实验所用的辐射井缩微模型由7根辐射管和1个竖井组成(图1(b))。每根辐射管长253 mm，外径20 mm。辐射管上分布着梅花状的进水孔，孔径5 mm。辐射管间的水平夹角为22.5°，仰角为15°，一端封闭，另一端通过连接头与竖井相连。为了对辐射井的计算模型进行验证，一共设计了相互组合的6种实验方案(2种河流渗漏补给能力×3种降深)。

图1 砂槽实验装置示意图及辐射井缩微模型

本次实验选择粒径为0.25～1.0 mm的中粗砂作为充填材料，在装砂之前，对砂子进行充分水洗、筛分，并去除其杂质。在砂槽底部铺1层厚度约为80 mm的卵石层，保证饱水时水流能够从砂槽底部均匀上升。同时在砂槽的4个侧壁铺上1层薄砂，以增加侧壁的粗糙度，减少侧壁效应的影响。填砂过程中需要逐层装填，使砂层分布均匀，填砂厚度为970 mm。

2.2 砂槽物理实验过程

安装完所有的实验仪器后，打开砂槽底部的4个进水阀门，控制进水从砂槽底部缓慢上升，尽可能排除砂槽中的气泡，以减少对实验的影响，注满整个砂槽的过程一般需要24 h。本次实验全部采用蒸馏水以减少水中离子或胶体产生的絮凝作用。模拟强渗漏补给河流时，在河流与含水层之间铺上透水性较好的纱网；模拟弱渗漏补给河流时，则铺上透水性较差的彩条布。实验开始前，关闭底部的进水阀门。通过顶部的水箱给砂槽供水，并保持“河流”水位为定值，多余的供水从砂槽一端的溢流槽流出。实验开始时记录所有仪器的初始值，然后打开竖井的放水阀门，等到流量与水头稳定时记录仪器数据。依次完成3个降深，结束实验。

3 数值模型的建立与拟合

3.1 数值模型的建立

在数值模型的建立中，砂槽区域的概念模型相对简单，砂槽四壁和底部都可以用零流量边界概化。数学模型与潘治霖[20]所描述的数学模型一致。

3.2 数值模型的求解与拟合

采用地下水流数值模拟软件MODFLOW进行求解。模型一共剖分为15行×91列，垂向上剖分为24层(辐射管位于第16层，平管位于第17层)。调整数值模型中含水层渗透系数K以及河流渗漏补给性能C值(conductance)，使模型计算流量及模拟水位降深与砂槽物理实验实测值相拟合，最终拟合结果见表1和图2。由表1可见，数值模型计算流量与实测流量的绝对差值在0.000 6～0.010 6 L/s之间，最大相对误差为3.24%；由图2可见，各实验方案数值模型模拟水位降深与实测水位降深误差均很小，除个别观测点外，误差均在±0.03 m以内，满足模型精度要求。

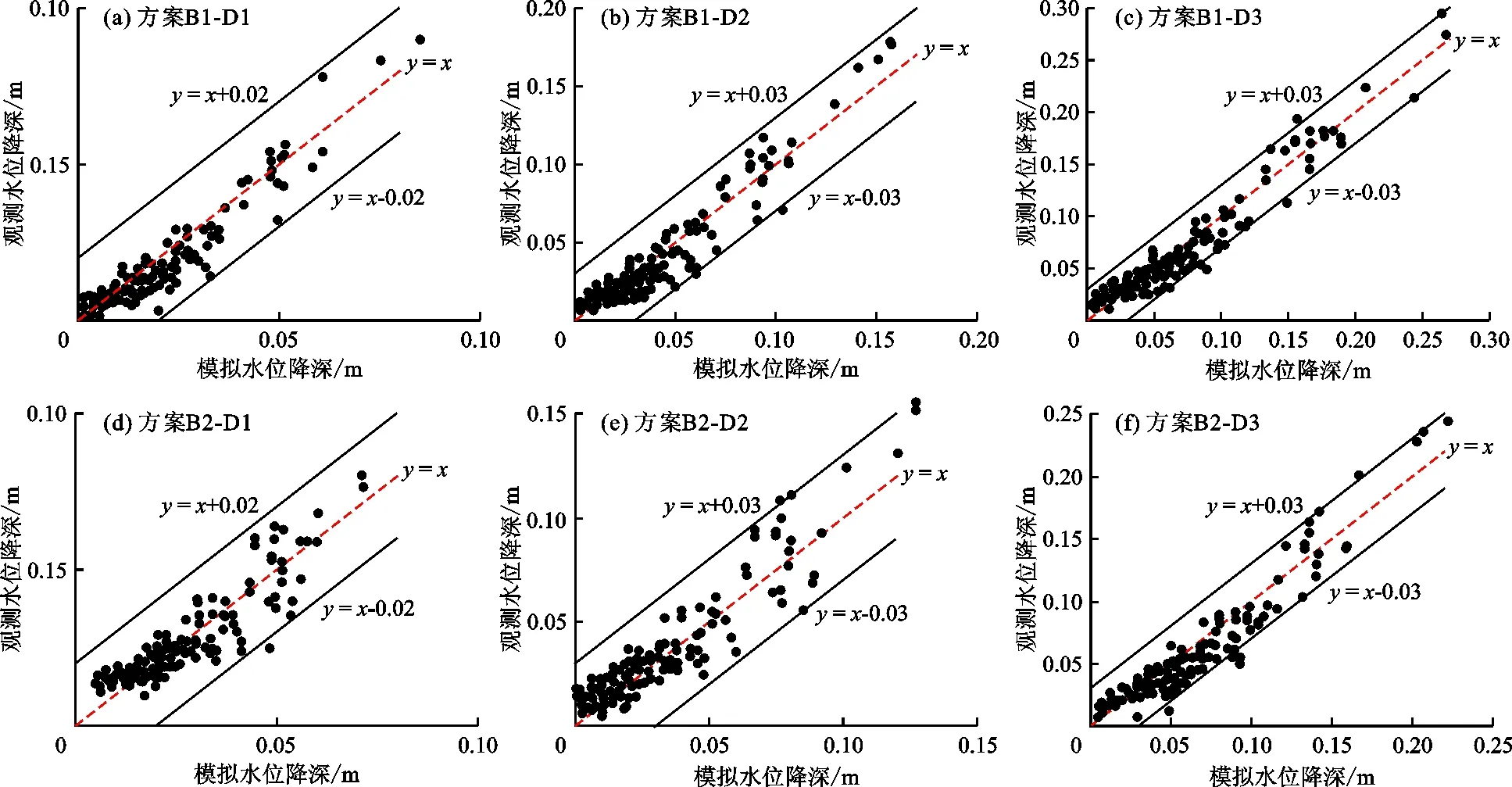
图2 各实验方案数值模型模拟水位降深与实验观测孔水位降深拟合结果

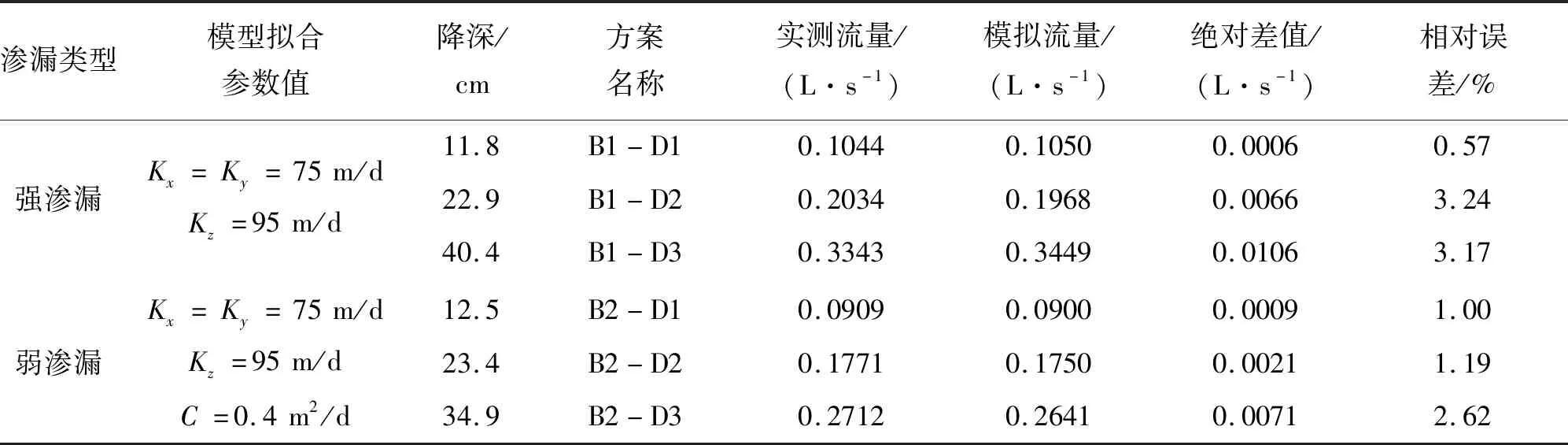
表1 各实验方案数值模型计算流量与砂槽物理实验实测流量拟合结果

数值模型拟合的渗透系数(粗砂为20～50 m/d、均质粗砂为60～75 m/d)大于经验值的原因可能是：实验前砂子经过了充分的水洗、筛分，并且在实验中重复利用多次，造成部分细小颗粒的流失，同时砂层经水沉作用填埋好后，并没有经过夯实，导致砂层的密实性较差，结构相对于实际地层蓬松，致使其渗透系数偏大。

4 辐射井取水效果影响因素的分析与讨论

为分析影响辐射井取水效果的因素并确定辐射井的最优结构，以洛河金鼎水源地为研究区，设计不同的方案讨论辐射井取水效果的变化。具体思路为：以具有3根长为50 m、仰角为25°、辐射管埋深为30 m的辐射井为初始方案，沿着垂直河流的方向，整体移动辐射井系统，由此可以确定最优的辐射管末端位置；辐射管末端位置确定后，沿着垂直河流的方向移动竖井(辐射管的长度和仰角都会变化)，确定竖井的位置；辐射管末端和竖井位置确定后，改变辐射管仰角(辐射管水平投影长度不变)，确定辐射管仰角；仰角确定后，增加辐射管根数，确定最优的辐射管根数；辐射井结构确定后，讨论渗透系数、河流深度、向竖井所在河岸增加辐射管对辐射井取水效果的影响。

4.1 研究区水文地质概况与模拟

研究区洛河金鼎水源地位于陕西省志丹县金鼎镇，年平均降水量为474.5 mm。研究区含水层类型为第四系全新统冲积层及白垩系环河组砂泥岩含水层，含水层总体厚度较大，为非均质轴对称各向异性介质，即Kx=Ky≠Kz。天然条件下，研究区内地下水的主要补给来源为大气降水入渗、地下水侧向径流以及农田回归灌溉。区内地下水径流、排泄主要受地形条件控制，地下水顺地势由东、西两侧向河流汇流，然后自北向南径流，排泄方式主要为向地表水排泄、少量的人工开采以及河流下游边界以地下水侧向径流排泄。

洛河及其上下游断面均概化为第一类定水头边界。模拟区周边边界为分水岭，可概化为第二类零流量边界。模拟区的上边界为潜水面边界，接受大气降水入渗补给，下边界为隔水边界。

4.2 数值模型的应用

将前文中拟合后的辐射井计算模型应用于洛河金鼎水源地，改变该模型的边界条件和模拟区的剖分网格，对辐射井的取水量进行计算。采用100 m×100 m的正交网格对平面区域进行划分，在河流区域采用20 m×20 m的正交网格进行加密处理，将辐射管部分进一步加密，精细划分为1 m×1 m的网格。将计算域剖分为362行、769列，垂向上共剖分为22层。

区内含水层可分为第四系松散岩类孔隙潜水含水层和白垩系环河组碎屑岩类裂隙孔隙含水层，第四系含水层与下伏白垩系环河组含水层有密切水力联系。根据钻孔抽水试验资料，河谷区第四系水平渗透系数为1.92 m/d，白垩系环河组的水平渗透系数可确定为0.15 m/d，各层的垂向渗透系数均设定为水平渗透系数的1/10。

模拟区两侧为分水岭，顶部为潜水面边界，河谷区大气降水入渗补给强度为118.5 mm/a(多年平均降水量为474.5 mm，大气入渗补给系数按0.25计)。山区黄土层的大气降水入渗补给强度为47.5 mm/a(大气入渗补给系数按0.1计)。洛河及其主要支流设置为第一类定水头边界。

4.3 结果分析与讨论

辐射井的结构主要由辐射管末端位置、竖井位置、辐射管根数和辐射管仰角确定。不同井结构条件下辐射井的取水量计算结果见表2。由表2可见，在确定辐射管末端位置时，辐射管完全穿过河流时(河流宽度为20 m)的取水量最大，这是因为辐射管末端完全穿过河流时，能同时激发河流两侧的地下水补给。应该指出，这一结论建立在辐射管的水平投影长度大于河流宽度的基础上，若辐射管的水平投影长度小于河流的宽度，则可能得到不同的结论。

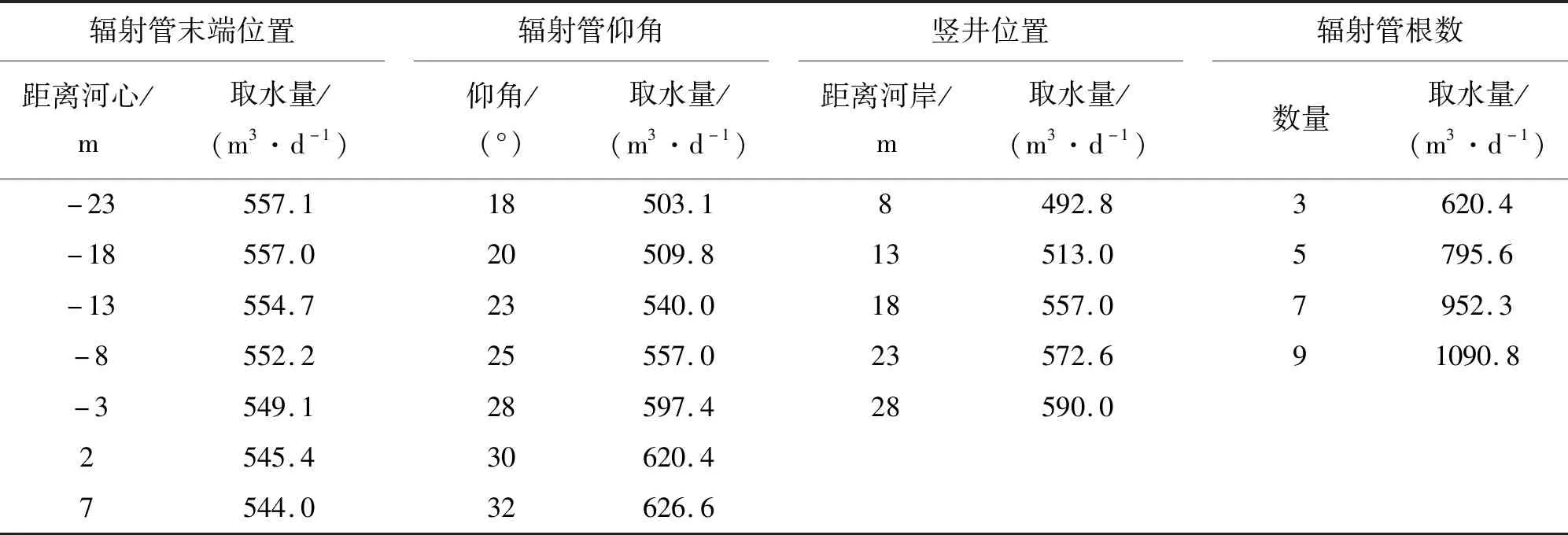
表2 不同井结构条件下辐射井的取水量

利用逐步优选的方法，将辐射管末端固定在距离河心-18 m处，移动竖井，可得到不同竖井位置下辐射井的取水量(表2)。考虑到竖井远离河岸的过程中，辐射管长度和取水量会同时增加。因此，本文综合考虑取水量和取水效率来确定最佳的竖井位置。取水效率用单位长度辐射管的取水量来衡量。辐射井的取水量和取水效率随竖井位置的变化曲线见图3。

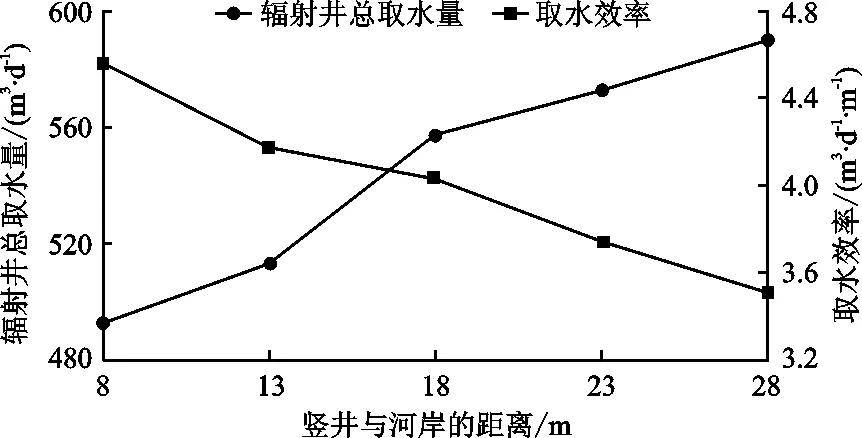
图3 辐射井的取水量和取水效率随竖井位置的变化曲线

由图3可以看出，辐射井的取水效率随着竖井的远离持续降低。在竖井与河岸相距约18 m时，既能满足一定的取水量，又能保证辐射井的取水效率处于较高的水平，因而在此处布设竖井的效果较好。应该指出，这个结论是在辐射管末端完全穿过河流且距离河心18 m时得到的。若辐射管末端位于其他位置，竖井的最佳位置可能略有差异，但辐射井取水效率随着竖井的远离而降低的趋势不会改变。

由计算结果(表2)可以看出，辐射井的取水量随着辐射管仰角、辐射管根数的增加而增加。但实际情况中并不是辐射管仰角越大、数量越多越好。因此，为确定辐射井的最优结构，仍然需要从辐射井取水效率的角度去考虑。辐射井的取水量和取水效率随辐射管仰角的变化曲线见图4。需要说明的是，辐射管末端位置和竖井位置均确定后，随着辐射管仰角的增加，辐射管的长度随之增加。图4表明，辐射井的取水效率随着辐射管仰角的增加呈现先增大后减小的趋势，辐射管仰角为30°时，取水效率达到最高。这是因为随着辐射管仰角的增大，辐射管与河床的距离变短，取水效率升高，但辐射管仰角进一步增大会使辐射管间的相互影响加大，最终导致取水效率降低。因此，辐射管的仰角可以设计为30°，这样既能满足一定的取水需求，又能使辐射井的取水效率处于较高的水平。

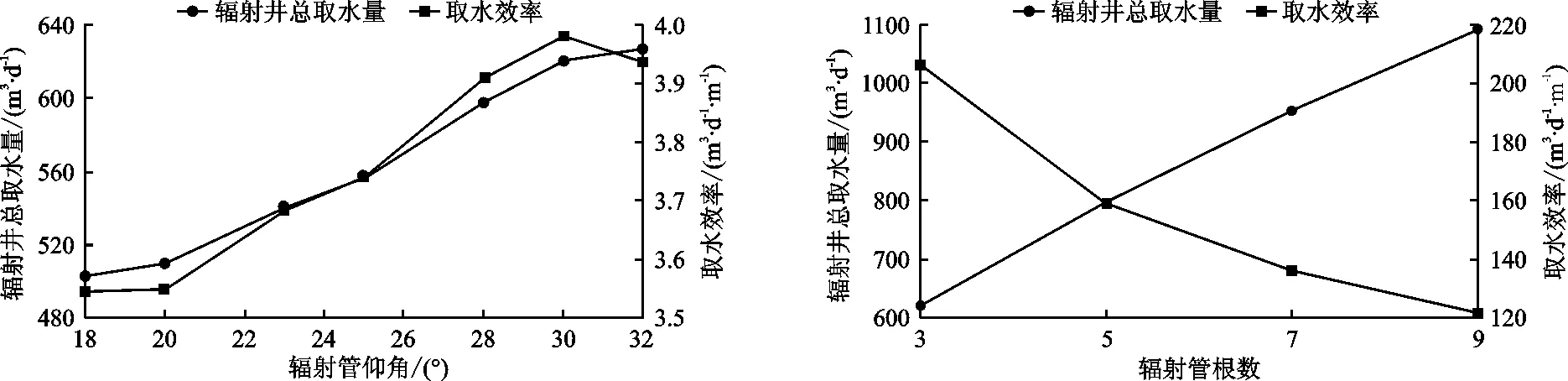
图4 辐射井的取水量和取水效率随辐射管仰角的变化曲线 图5 辐射井的取水量和取水效果随辐射管根数的变化曲线(辐射管仰角为30°)

在辐射管仰角为30°的条件下，辐射井的取水量和取水效率(此时取水效率以单根辐射管的取水量衡量)随辐射管根数的变化曲线见图5。从图5可以发现，辐射管根数由3增加到9时，辐射井的取水效率几乎降低一半，这是因为随着辐射管根数的增加，辐射管之间的相互影响也随之增大，因而取水效率明显降低。因此，辐射管的根数不宜过多，在满足取水需求的条件下，以5～7根为宜。

确定辐射井的结构后，通过计算来讨论辐射管埋深、河谷区渗透系数、河流深度等对辐射井的取水量的影响。在7根仰角为30°的辐射管的条件下，设计不同方案进行计算，计算结果见表3。由表3可以看出，辐射井的取水量随着辐射管埋深的增加而减少，随着渗透系数的增加而增大，随着河流深度的增加而增大。由达西定律Q=K·I·A(Q为取水量，m3/d；K为渗透系数，m/d；I为水力坡度；A为渗流断面面积，m2)可知，辐射管埋深增大，则水力坡度减小，而渗透系数直接影响辐射井的取水量。河流的深度影响的是河床的渗透性能，河流深度越大，则河床的渗透性能越好。因此，在实际施工过程中，辐射井应该尽量布设在渗透系数较大、河流较深的区域，以获得更好的取水效果。

由表3还可以看出，在竖井所在的河岸增加一根辐射管后，辐射井的取水量明显增加。位于河床下的7根辐射管的取水量主要来自河流，而新增加的辐射管的取水量主要来自河谷区的地下水。从两种方案的潜水面降深等值线图(图6)可以看出，在竖井所在河岸增加1根辐射管后，引起的附加水位降深很小。因此，在实际的施工过程中，如果在河岸增加辐射管不会引起河谷区产生较大的附加水位降深，则可以在竖井所在河岸增加辐射管，以获得更好的取水效果。

表3 不同方案下辐射井的取水量(辐射管为7根，仰角为30°)

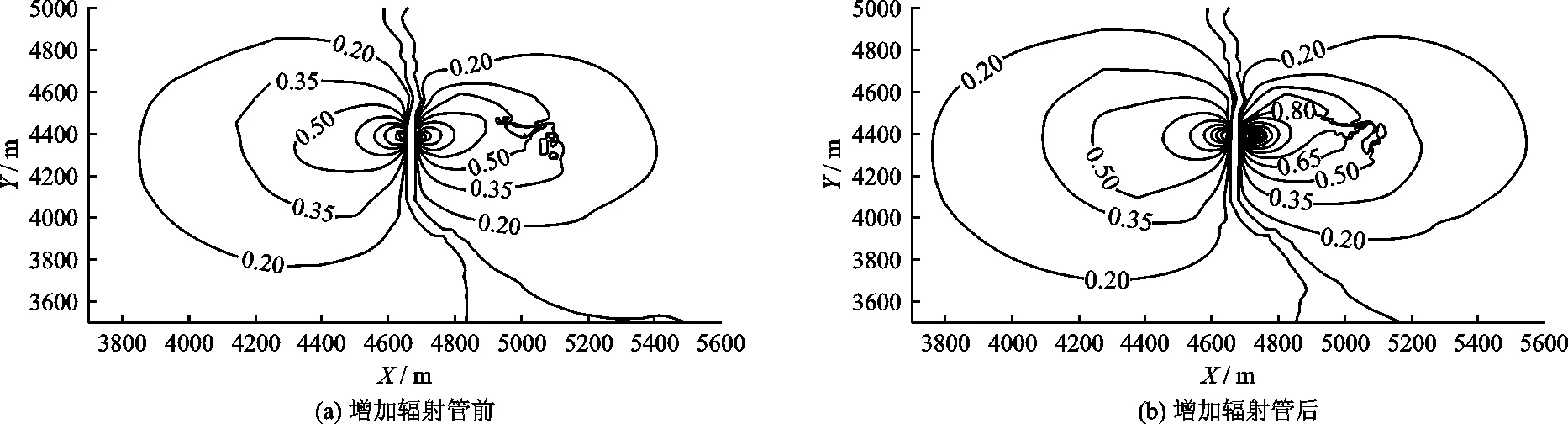
图6 增加辐射管前后潜水面降深对比(单位：m)

5 结 论

本文对辐射井的计算模型进行拟合验证，并将验证后的模型应用于洛河金鼎水源地，对不同辐射井结构下的取水效果进行分析，得到以下主要结论：

(1)利用MODFLOW软件，将井管看作离散的节点、将含水层中的渗流与井管中的管流进行耦合的方法计算辐射井的取水量是合理的。

(2)辐射井的取水效果与辐射井的结构、含水层性质、河流深度等影响因素密切相关。一般情况下，辐射井的取水量和取水效果并不能同时兼顾，在实际施工过程中需要综合考虑。

(3)在不引起竖井所在河岸地下水位大幅度下降的条件下，可以在竖井所在河岸增加1根辐射管，以获得更好的取水效果。