不同支付方式下城市轨道交通检票闸机通过能力研究

马超群，王 云，宁 静，张 勇

（1. 长安大学 运输工程学院，陕西 西安 710064；2.西安市政设计研究院有限公司 第四市政设计研究分院，陕西 西安 710068)

0 引言

自动检票闸机作为分隔城市轨道交通车站付费区与非付费区的标志，在客流高峰时期，往往会聚集大量乘客造成排队现象，成为城市轨道交通车站的瓶颈，因而加强检票闸机通过能力研究可以为解决进出站拥堵、确定检票闸机配置数量等提供依据。

近年来，一些学者进行相关研究：周慧娟等[1]基于Delphi和改进模糊层次分析法建立自动检票闸机通过能力评价指标体系，机器自身性能、数量、设置位置及客流特征是影响检票闸机组通过能力的重要指标；吴娇蓉等[2]通过研究得出性别对通过检票闸机时间间隔无显著影响，携带包裹的大小、持卡类别、年龄及熟练程度对通过检票闸机时间间隔有显著影响；覃松涛等[3]得出三杆式检票闸机的实际通过能力为1 058人次/h，门扉式检票闸机的实际通过能力为1 480人次/h；刘双庆等[4]对地铁车站晚高峰时段客流进行视频录像，采用逐帧回放的方式，统计乘客连续通过检票刷卡的速度和乘客通过检票闸机的间隔时间；冯建栋等[5]研究检票闸机组空间利用不均衡度及时间利用不均衡度与路径选择的关系；王子甲等[6]和付佳等[7]通过仿真验证垂直人行路径和平行人行路径的检票闸机布局形式对检票闸机组通过能力的影响。因此，检票闸机类型与乘客特征及检票闸机布局对检票闸机的通过能力有所影响。

随着智慧城市轨道交通的建设，除传统的使用磁卡和非接触IC卡进出站外，人们逐渐使用移动扫码支付进出站的形式。移动扫码支付是通过识别乘客手机软件乘车二维码控制进出检票闸机的方式，支付方式或者持卡类别对通过检票闸机时间具有显著影响。以西安地铁小寨站工作日晚高峰期间进站客流为例，对不同支付方式下的检票闸机通过能力进行分析，将进站乘客按支付方式分类，并统计不同支付类型下乘客所需检票闸机服务时间，进而研究检票闸机类型为门扉式检票闸机、设置位置垂直于客流步行走向的情况下进站检票闸机的通过能力，优化车站检票闸机配置，解决高峰时段进出站拥堵问题。

1 不同支付方式下城市轨道交通检票闸机通过能力

1.1 自动检票闸机

自动检票闸机是城市轨道交通自动售检票系统的组成部分。设置检票闸机的目的是为了保证客流能够有序、顺利地进出车站并完成计费[8]。其按照功能分为进站、出站和双向检票闸机，按拦截方式可以分为三杆式和门扉式。进站方向的门扉式检票闸机的长度为1.85 m，布置间隔为0.65 m。检票闸机属于车站乘客服务设施中的节点类设施，乘客在通过检票闸机的过程中，包括减速、排队、刷卡、等待、通过等行为[9]。自动检票闸机每次开启仅供1名乘客(或乘客带小孩)通过，乘客通过自动检票闸机示意图如图1所示。图中A，B，C，N表示乘客；①，②，③表示位置。

具体流程为：乘客A在位置①检票，门扉打开后前进，到达位置②；乘客B到达位置①，准备检票，同时观察A；乘客B观察乘客A到达位置③，B即开始检票；乘客A从位置①到达位置③，完成整个通过检票闸机过程；其他乘客重复乘客A的过程，直至所有乘客均通过检票闸机。

1.2 不同支付方式下检票闸机通过能力分析

检票闸机通过能力是指单位时间内允许乘客连续不断通过检票闸机的人数，检票闸机服务时间是影响检票闸机通过能力的决定性因素。进站支付方式对进站的方便程度和检票闸机的反应时间有显著影响。据调查，目前地铁车站自动检票闸机实现的进站支付方式包括3类：磁卡(单程地铁票)、非接触IC卡(城市一卡通)及地铁乘车码(移动扫码支付)。磁卡和非接触IC卡支付检票方式是乘客刷卡后检票闸机直接识别卡内信息，而移动扫码支付检票方式是检票闸机通过识别乘客手机软件中的二维码信息完成检票。由于进站时磁卡和非接触IC卡感应识别无明显差异，同时城市工作日高峰时段使用磁卡(单程地铁票)进站乘客占比较少(为2.5%)，因而主要针对移动支付和刷卡支付的进站方式进行研究，其中地铁乘车码为移动支付，磁卡和非接触IC卡为刷卡支付。

检票闸机通过能力计算公式为

式中：C为单个检票闸机实际通过能力；γ，β分别为刷卡支付和移动扫码支付乘客使用比例；t1，t2分别为使用刷卡支付和移动支付乘客所需检票闸机服务的平均时间。

其中，乘客刷卡支付所需检票闸机服务时间和移动扫码支付进站所需检票闸机服务时间均服从对数正态分布，对应的概率密度函数为

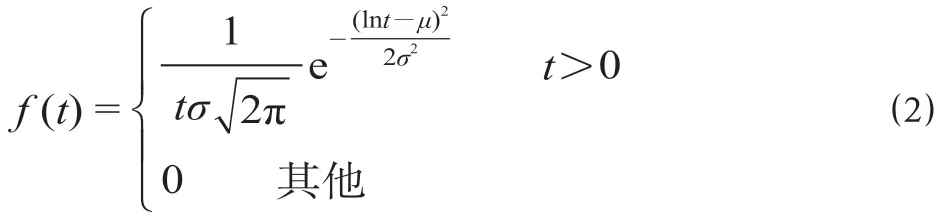
式中：t为检票闸机服务时间；μ为lnt的均值；σ为lnt的标准差。

1.3 西安地铁检票闸机通过能力分析

通过对西安地铁进站客流高峰时期的观测，乘客实际占用检票闸机的时间t由以下2部分组成。一是乘客到达位置①后到开始识别的准备时间，乘客的熟悉程度、进站前是否提前准备好交通卡或者提前打开二维码等行为产生的影响都反映在内；二是乘客从位置①识别进入检票闸机到达位置③所需的检票闸机服务时间。统计每个乘客所需检票闸机服务时间应将乘客的准备时间和通过占用时间都考虑在内。

由于车站客流呈现不均衡性，连续通过检票闸机的乘客状态更符合求取通过能力的数据状态，因此研究对象应选择客流量大的地铁车站。西安地铁小寨站是地铁2号线和3号线的换乘站，位于西安城市副中心小寨片区，车站周边用地开发强度大，以商业及办公用地为主，客流量大。基础数据选用小寨站工作日晚高峰期间(18 : 00—19 : 00)进站客流通过检票闸机的时间数据，前期采用录制视频获取原始资料，后期利用软件编写精确度为1.0 ms的计时器读取视频时间数据，每组数据读取3次取其平均值。

2 刷卡支付城市轨道交通检票闸机服务时间分析

2.1 刷卡支付检票闸机服务时间对数分布拟合

刷卡支付所需检票闸机服务时间是否服从正态分布，可以采用峰度(Kurtosis)和偏度(Skewness)来判断。峰度是描述某变量所有取值分布形态陡缓程度的统计量，是和正态分布相比较的。当峰度= 0时，与正态分布的陡缓程度相同；当峰度＞ 0时，比正态分布的高峰更加陡峭；当峰度＜ 0时，比正态分布的高峰平缓。偏度是衡量数据偏斜方向和程度的度量，即非对称程度。偏度= 0时，概率密度函数左右对称；偏度＞ 0时，对应分布正偏(左偏)；偏度＜ 0时，对应分布负偏(右偏)。偏度系数的绝对值越大，数据偏离度越大，中位数和平均值显著偏离。如果数据服从正态分布，那么峰度、偏度应均为0。

刷卡支付进站乘客占用检票闸机服务时间描述统计如表1所示。从表1中看出，峰度和偏度分别为1.770，1.012，因此，刷卡支付检票闸机服务时间不符合正态分布。基于刷卡支付检票闸机服务时间的数据分布特征，假设其服从对数正态分布，并进行假设检验。

表1 刷卡支付进站乘客占用检票闸机服务时间描述统计Tab.1 Statistics of gate service time for card payment

刷卡支付检票闸机服务时间对数正态Q-Q图如图2所示。对数据分布情况进行分析，数据越接近表示越服从该分布，比较发现乘客所需检票闸机服务时间接近对数正态分布。进而拟合得到相应的概率密度分布图像，刷卡支付检票闸机服务时间对数分布图如图3所示。

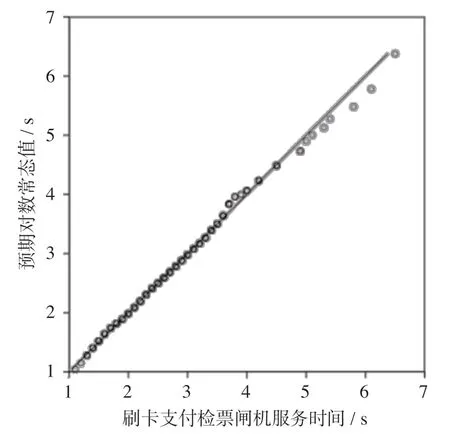
图2 刷卡支付检票闸机服务时间对数正态Q-Q图Fig.2 Lognormal distribution Q-Q graph of service time for card payment

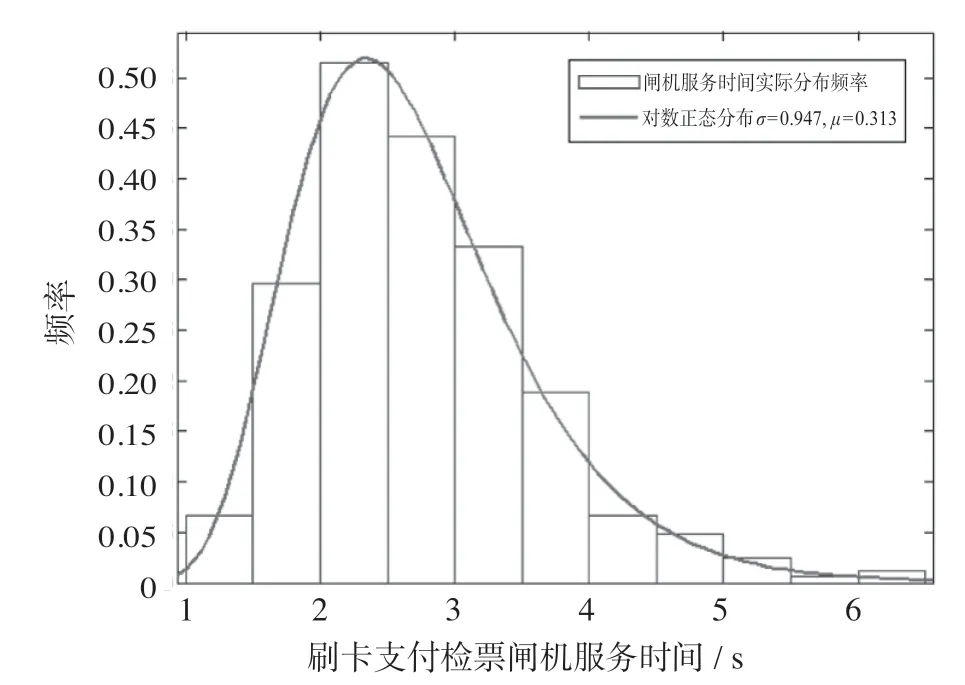
图3 刷卡支付检票闸机服务时间对数分布图Fig.3 Logarithmic distribution of gate service time for card payment

由图3可知，乘客刷卡支付所需检票闸机服务时间近似服从均值μ为0.947、标准差σ为0.313的对数正态分布，对应的概率密度函数f(t1)为

2.2 卡方检验

对上述频率分布拟合优度进行卡方检验。卡方检验描述统计样本的实际观测值与理论推断值之间的偏离程度。卡方值越大，表示越不符合；卡方值越小，偏差越小，越趋于符合假设。定义卡方检验的原假设H0为样本的总体分布符合所采用的理论分布。卡方值χ2计算公式为

式中：mi为第i个区段的实际频数；n为总样本量；pi为第i个区段的理论频率；k为计算卡方值时分段的组数。

对于离散数据，采用卡方检验时，各分组理论频数应不小于5，并且需要满足总样本量n≥40。刷卡支付检票闸机服务时间的实际频率与理论频率比较如表2所示，从中可以看出刷卡支付检票闸机服务时间主要集中在1.5 ～ 4 s范围内，闸机服务时间超过4 s后分布较为离散。

表2 刷卡支付检票闸机服务时间的实际频率与理论频率比较Tab.2 Comparison between actual frequency and theoretical frequency of gate service time for card payment

当显著水平α= 0.05，H0成立时，卡方值不应过大，有拒绝域

式中：s为用样本估计总体的参数个数。

在该案例中分段组数k= 9，样本估计总体的参数个数s= 2，则可以计算卡方值χ2= 4.104。在单侧95%置信度水平下查表得12.592，显然，有(6)，说明接受原假设，即该组数据服从对数正态分布。由此可知，使用刷卡支付进站乘客所需检票闸机服务时间t1服从均值μ= 0.947、标准差σ= 0.313的对数正态分布。则利用公式 ⑴ 可以计算得到，全部使用刷卡方式进站情况下城市轨道交通检票闸机实际的通过能力为1 396人次/h。

3 移动支付城市轨道交通检票闸机服务时间分析

3.1 移动支付检票闸机服务时间对数分布拟合

关于使用移动支付进站乘客所需检票闸机服务的时间分析，采用相同的办法对数据进行统计研究，移动支付进站乘客占用检票闸机服务时间描述统计如表3所示。

表3 移动支付进站乘客占用检票闸机服务时间描述统计Tab.3 Statistics of service time for mobile payment

从表3中看出，峰度和偏度均大于1，可见移动支付检票闸机服务时间也不服从正态分布。同理，采用Q-Q图进行探索分析，移动支付检票闸机服务时间对数正态分布Q-Q图如图4所示。比较分析表明在选用对数正态分布拟合时，图中数据点最接近分布于直线周围，认为数据大致服从对数正态分布，移动支付检票闸机服务时间对数分布图如图5所示。

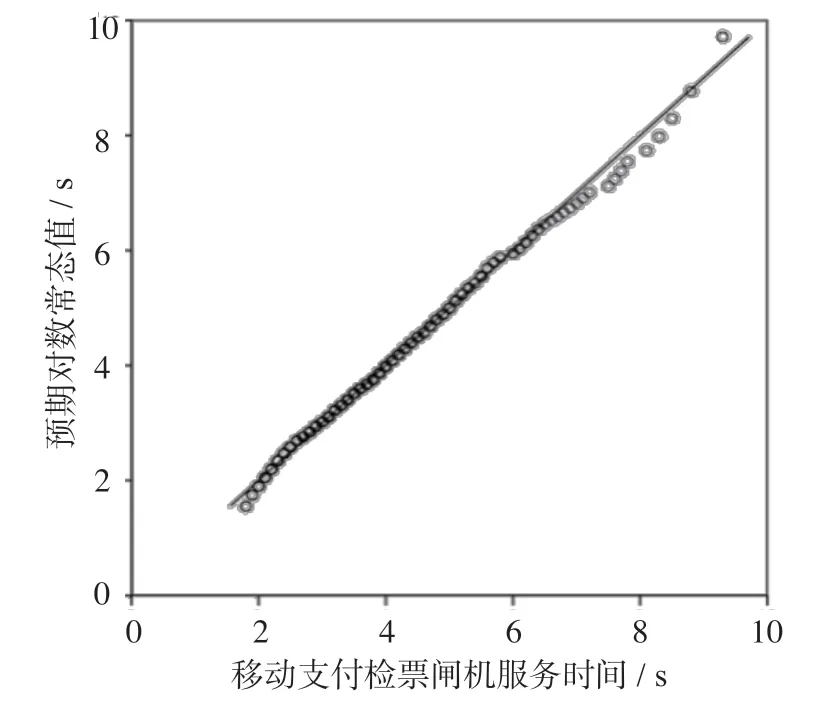
图4 移动支付检票闸机服务时间对数正态分布Q-Q图Fig.4 Lognormal distribution Q-Q graph of gate service time for mobile payment

乘客移动扫码支付进站所需检票闸机服务时间近似服从均值为μ= 1.326、标准差为σ= 0.327的对数正态分布，对应的概率密度函数f(t2)为

3.2 卡方检验

同样采用卡方值进行检验，移动支付闸机服务时间实际频率与理论频率比较如表4所示。从中可以看出，移动支付闸机服务时间主要集中在1.2 ～ 6.0 s区间范围内，占样本总数的92.3%，其中2.4 ～ 4.8 s区间范围占样本总数的67.1%。

在该案例中分段组数k= 10，样本估计总体的参数个数s= 2，则计算卡方值χ2= 3.644。在单侧95%置信度水平下查表可得，显 然，有，说明接受原假设，即该组数据服从对数正态分布。由此可知，使用移动支付进站乘客所需检票闸机服务时间t2服从均值μ= 1.326、标准差σ= 0.327的对数正态分布。则利用公式 ⑴ 可以计算得到，完全使用移动支付方式进站情况下，城市轨道交通检票闸机实际的通过能力为956人次/h。

图5 移动支付检票闸机服务时间对数分布图Fig.5 Logarithmic distribution of gate service time for mobile payment

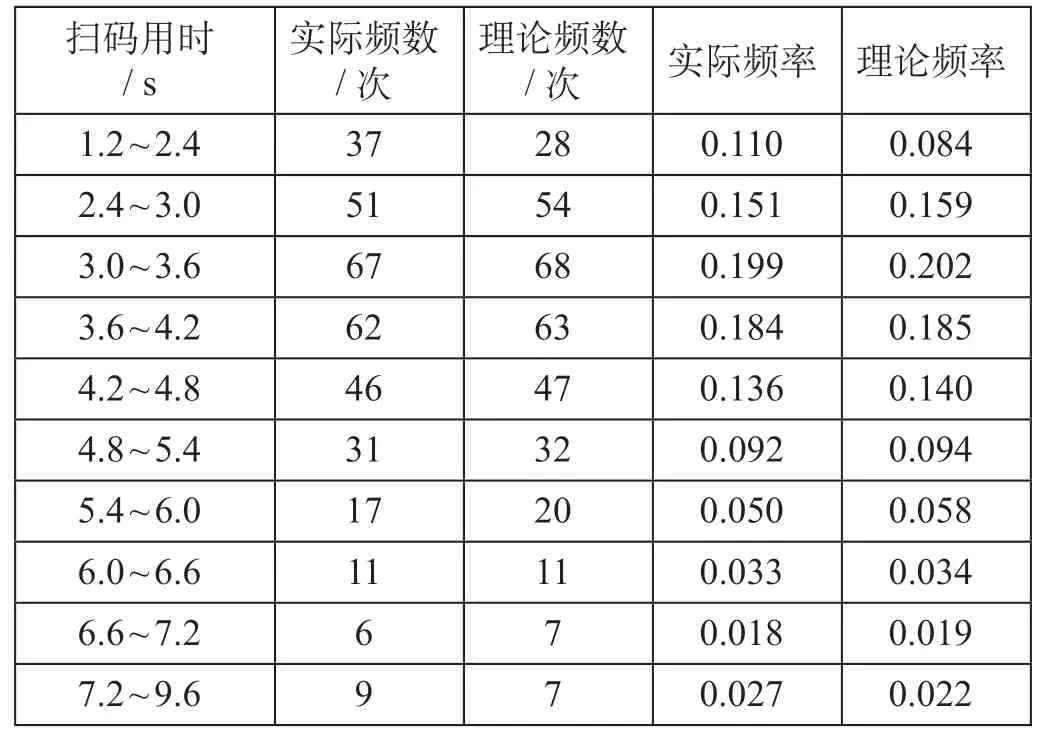
表4 移动支付闸机服务时间实际频率与理论频率比较Tab.4 Comparison between actual frequency and theoretical frequency of service time for mobile payment

乘客移动支付下检票闸机通过能力比刷卡支付下小440人次/h，差异显著。究其原因，一方面是由检票闸机的扫码系统和刷卡系统本身的差异造成的，且相比刷卡通过检票闸机，乘客对移动扫码的熟悉操作程度较低；另一方面，通过检票闸机时，扫码支付乘客需进行准备手机、打开软件、找到乘车码等行为，比刷卡通过复杂，导致乘客对于扫码时的准备时间大于刷卡乘客的准备时间。

4 研究结论

（1）检票闸机实际通过能力为车站检票闸机数量配置提供重要依据。《地铁设计规范》中给出门扉式检票闸机刷卡方式为非接触IC卡时的通过能力推荐值为1 800人次/h，而实测通过能力仅为1 396人次/h，远低于规范推荐值；而使用移动扫码支付的检票闸机实际通过能力为956人次/h。

（2）对于门扉式检票闸机，刷卡支付方式下乘客进站检票闸机服务时间服从均值μ= 0.947、标准差σ= 0.313的对数正态分布；移动扫码支付方式下乘客进站检票闸机服务时间近似服从均值μ=1.326，标准差σ= 0.327的对数正态分布。

（3）随着智慧城市及智能交通的建设，城市轨道交通自动检票闸机移动扫码支付方式将更加普及，在车站检票闸机布局设计中应对检票闸机通过能力按不同支付方式分类研究，结合车站客流强度、接受排队长度和排队等待时间等因素，合理确定检票闸机数量和布设方式。