考虑磁透镜边缘场的质子成像系统优化设计*

陈锋 郝建红 许海波

1) (中国工程物理研究院研究生院, 北京 100088)

2) (华北电力大学电气与电子工程学院, 北京 102206)

3) (北京应用物理与计算数学研究所, 北京 100094)

1 引 言

1995 年, 美国科学家Chris Morris 提出用质子代替X 光进行辐射照相, 与X 射线相比, 质子照相在穿透能力、密度分辨率和多次成像等方面有着明显的优势, 这为流体动力学实验的研究提供了一种先进的诊断方法[1,2].美国科学家通过800 MeV和24 GeV 的加速器验证了质子照相技术的空间分辨率、连续成像能力以及反准直器的应用[3−8].俄罗斯科学家通过800 MeV, 50 和70 GeV 的质子照相系统对流体动力学实验展开了研究[9−11].德国科学家利用4.5 GeV 的质子加速器进行了质子照相研究[12].中国原子能研究院设计了100 MeV的质子成像系统[13], 兰州近代物理研究所设计了600 MeV/u 的碳离子照相系统和800 MeV 的电子照相装置[14,15], 中国工程物理研究院对质子成像系统以及成像模糊等问题展开了研究[16,17], 清华大学展开了电子照相在高能量密度物理中的应用研究[18].

质子成像系统由两组四极磁透镜对和准直器组成, 如图1 所示.四极磁透镜使系统实现点对点成像, 角度准直器可以控制通量, 从而实现调节对比度、密度重建和材料诊断[19].理想磁透镜的磁场梯度在边缘处突变为零, 在透镜内部, 磁场梯度沿轴向为常数, 而实际透镜的磁场边界向外延伸, 如图2 所示.在质子成像系统中, 边缘场将影响质子的输运状态, 从而影响成像系统的性能.目前, 高能质子照相相关的研究中, 系统参数均是以理想透镜给出的[20−22], 没有考虑磁透镜边缘场以及其对质子通量的影响, 本文通过对四极透镜边缘场的研究, 给出了一种优化系统的方法.中国散裂中子源的质子能量是1.6 GeV, 本文给出了1.6 GeV 的成像系统考虑边缘场时的系统参数.通过数值模拟,研究了考虑边缘场的优化后的系统参数对准直器孔径的影响.通过对比使用理想系统、优化前后系统的质子通量分布, 研究了边缘效应对质子通量的影响.

图1 质子成像系统示意图Fig.1.Diagram of proton imaging system.

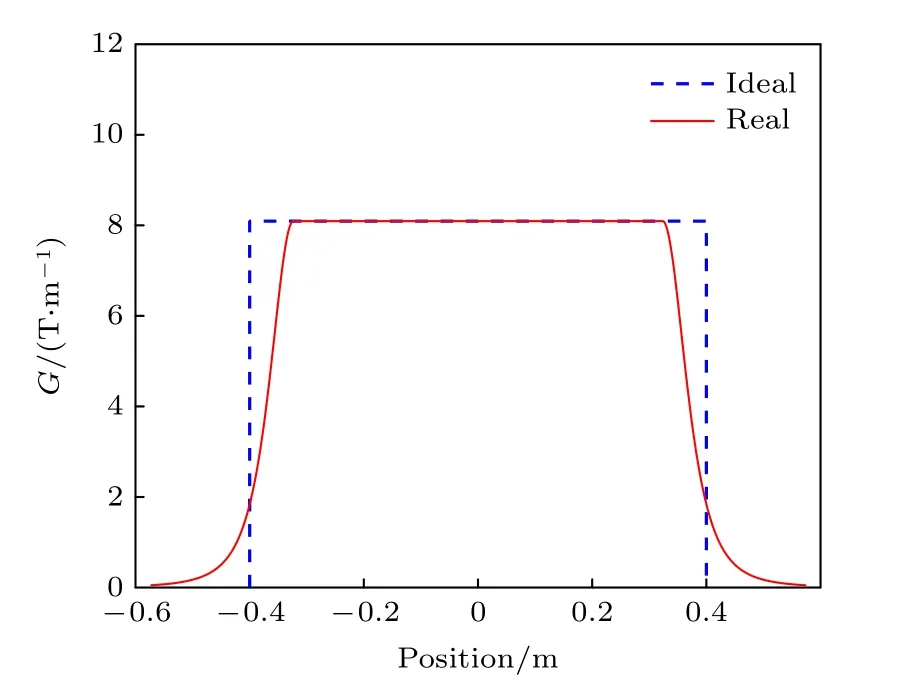
图2 磁透镜中磁场梯度分布Fig.2.Magnetic field distribution in the quadrupole lens.

2 考虑边缘场的成像系统优化方法

处理边缘场问题时, 可以用磁场梯度积分相等的矩形场近似实际场, 得出磁铁的等效长度:

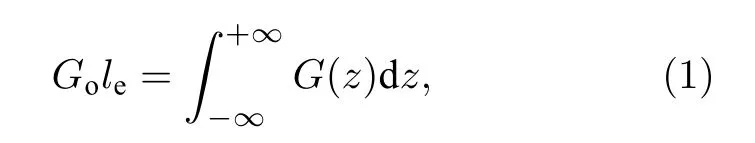
其中 Go为平坦区的磁场梯度值; le磁透镜的等效长度.此时原磁场分布区间的传输矩阵等效为两段等效漂移距离和理想四极磁透镜[23]:

其中 RB是原磁场分布区间的传输矩阵; S 是等效漂移段矩阵; M 是理想四极磁透镜传输矩阵.

根据(2)式可以得出等效漂移距离长度:

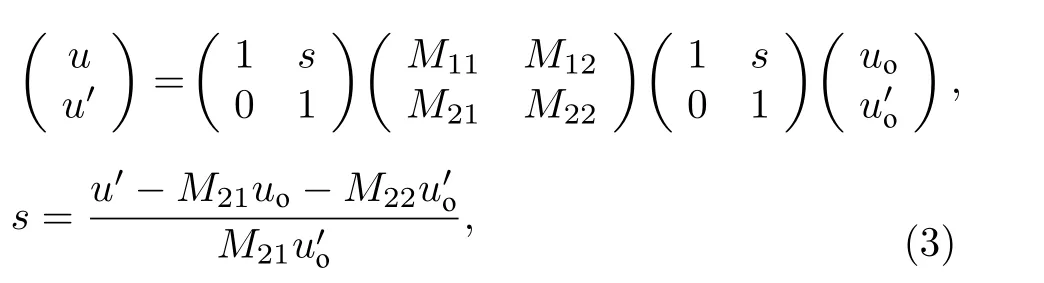
图3 等效漂移距离随着初始位置的改变Fig.3.Equivalent drift distance varies with the initial position.

设 so为系统中磁透镜的中心轴线上对应的等效漂移距离, s 为任意等效漂移距离, 记等效漂移距离相对值为 Δ s=s −so.记 (为客体平面坐标,为成像点坐标, 此时有

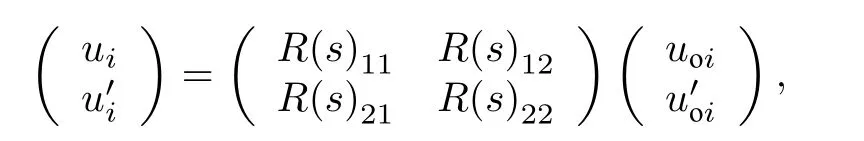
理想成像系统的传输矩阵 R =−I , 因此坐标误差可以写成

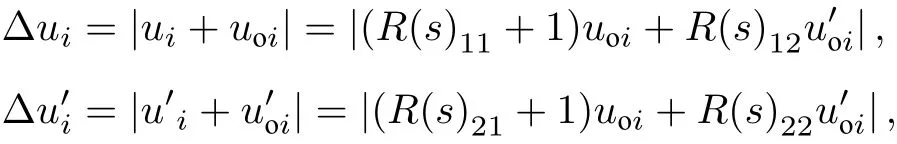
使得视场范围内坐标的平均误差值小于误差允许上限, 可得优化漂移距离的集合:

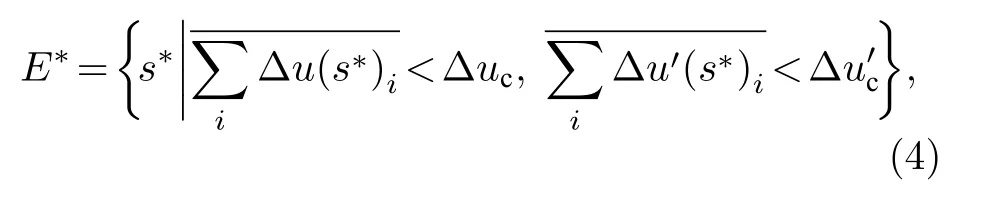
其中 Δ uc和表示误差的允许上限.以中心轴线上对应的等效漂移距离为初值, 并以等效漂移距离相对值 Δ s 为变量, (4)式可以写成:

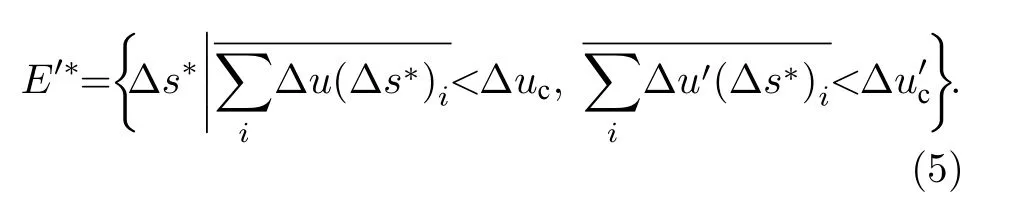
可以根据(5)式给出的方法得出优化漂移距离, 并通过蒙特卡罗模拟程序Geant 4[24,25]实现优化过程.具体步骤如下: 1) 通过Geant 4 模拟成像系统, 并设定等效漂移距离相对值的初值; 2) 随机产生初始质子, 计算质子在客体平面和成像平面时的位置误差和角度误差, 并求平均值; 3) 改变等效漂移距离相对值.重复步骤2)和3)可以得出一定范围内的等效漂移距离相对值所对应的平均位置误差和角度误差, 再根据误差允许上限可以选择出符合要求的等效漂移距离的相对值集合.质子照相中, 期望平均位置误差和角度误差均尽量小, 又要利用角度准直器进行角度截断, 因此可以通过绘制优化曲线来确定角度误差最小时的等效漂移距离相对值(mm 量级舍入).含边缘场的磁场梯度用贝尔函数近似[26]:

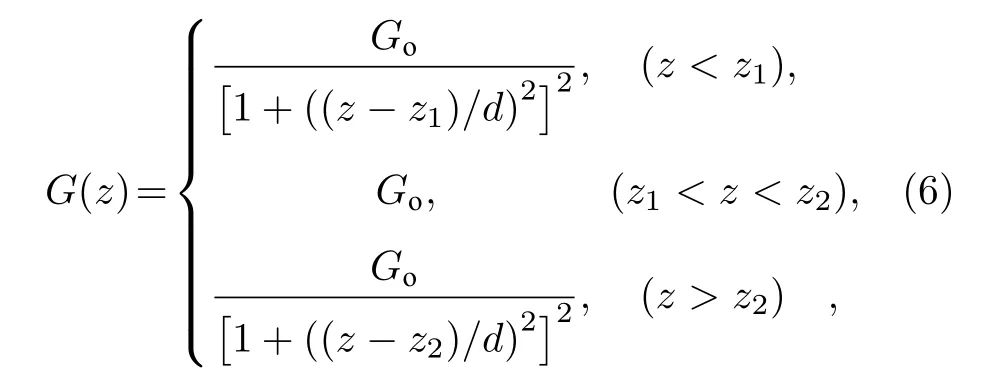
其中 Go是平坦区梯度值, d 是边缘场参数.本文采用1.6 GeV 的成像系统, 通过Geant 4 程序进行数值计算, 并使得理想透镜的梯度积分和含边缘场透镜的梯度积分的差值(积分差值)分别等于0 和1%.表1 列出了理想系统和含边缘场系统优化前(初值)的具体参数.图4 是质子成像系统参数示意图,其中 Ds是外漂移距离, F 是聚焦四极透镜, l 是透镜厚度, Dt是内漂移距离, D 是散焦四极透镜, cz 是准直空间.通过优化曲线可以得出等效漂移距离相对值, 从而得出优化后的成像系统中的漂移段长度.

通过(5)式可以得出磁铁的等效漂移距离相对值, 图5(a)是积分差值等于0 时的优化曲线, 可以得出等效漂移距离相对值等于3 mm.图5(b)是积分差值等于1%时的优化曲线, 可以得出等效漂移距离相对值等于8 mm.表2 列出了含边缘场系统优化后的参数.

表1 优化前质子成像系统参数Table 1.Parameters of the proton imaging system before optimization.

图4 质子成像系统参数示意图Fig.4.Diagram of parameters of proton imaging system.

图5 等效漂移距离相对值的优化曲线 (a) 积分差值为0;(b) 积分差值为1%Fig.5.Optimized curves of relative value of the equivalent drift distance: (a) The difference of integral value is 0;(b) the difference of integral value is 1%.

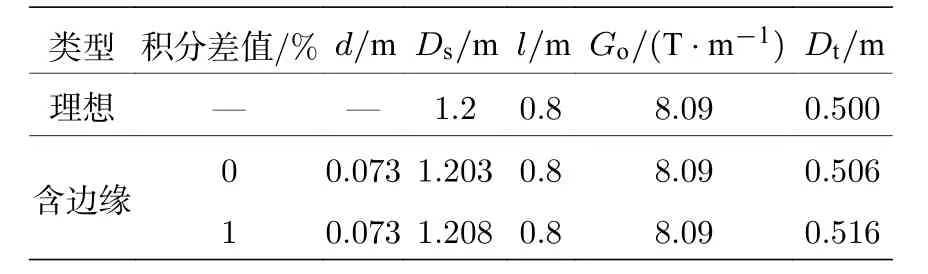
表2 优化后质子成像系统参数Table 2.Parameters of proton imaging system after optimization.

3 磁场边缘效应对准直器孔径的影响

质子成像系统如图1 所示.质子运动到中心平面时, 质子的位置仅与多次库伦散射角有关, 因此可以通过角度准直器控制质子通量, 从而实现调节对比度、密度重建和材料诊断.因此, 质子通量的准确性影响着重建密度的误差和材料诊断的准确性.角度准直器可以通过视场半径、截断角和传输矩阵进行设计, 椭圆台状的角度准直器能保证质子通量的准确性[27].

优化后的成像系统将改变传输矩阵, 从而影响准直器孔径形状.图6 和图7 分别是影响准直器前端和后端孔径的传输矩阵元 (m11和 m12)随积分差值变化的曲线, 积分差值的变化范围是(0, 7%).图6(a)是前端口x 方向的传输矩阵元变化曲线,其中 m11和 m12的最大变化量分别是2%和6%;图6(b)是前端口y 方向的传输矩阵元变化曲线,其中 m11和 m12的最大变化量分别是1%和4%;图7(a)是后端x 方向的传输矩阵元变化曲线, 其中m11和 m12的最大变化量分别是5%和4%; 图7(b)是后端y 方向的传输矩阵元变化曲线, 其中 m11和m12的最大变化量是分别是2%和4%.

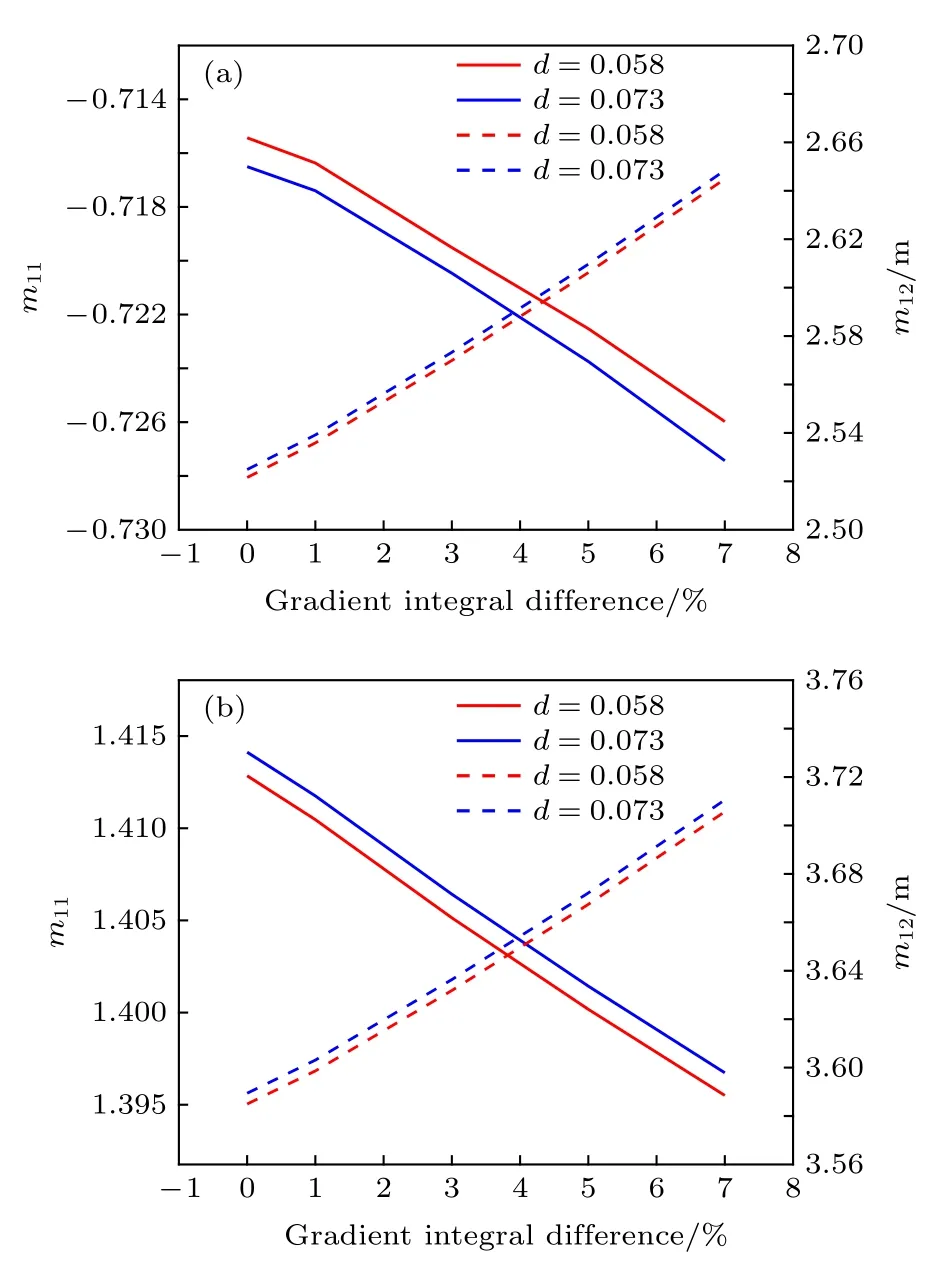
图6 前端口传输矩阵元随磁场梯度积分差值的变化(a) x 方向; (b) y 方向Fig.6.Transfer matrix elements of the front port varies with the gradient integral difference: (a) x direction; (b) y direction.

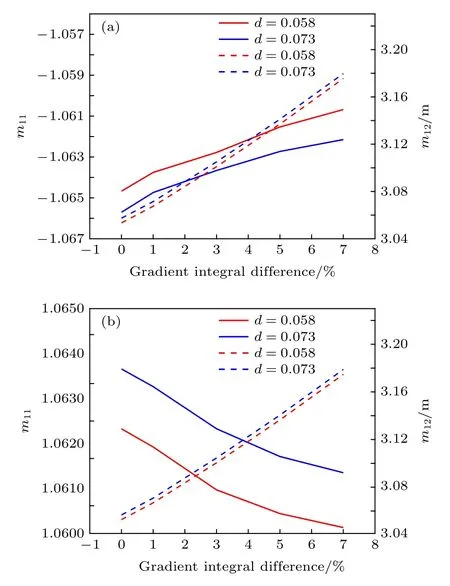
图7 后端口传输矩阵元随磁场梯度积分差值的变化(a) x 方向; (b) y 方向Fig.7.Transfer matrix elements of the back port varies with the gradient integral difference: (a) x direction; (b) y direction.

矩阵元随积分差值的变化基本呈线性关系, 各矩阵元的变化量均与积分差值大小在同一量级.当积分差值在10–2量级时, 准直器孔径参数的变化亦在10–2量级.

4 磁场边缘效应对质子通量的影响

通过对比理想磁透镜成像系统、优化前和优化后含边缘场的磁透镜成像系统中使用准直器时, 客体的通量分布进行分析磁场边缘对通量的影响.系统参数采用表2 给出的参数.准直器以视场半径6 cm、截断角2.0 mrad 和3.5 mrad 进行设计, 表3是准直器参数.本文对两种客体进行模拟, 客体1是厚度为1 mm、半径为5 cm 的铜板, 客体2 是同心球客体, 从内到外的半径依次是1, 4 和5 cm.材料分别是空气、锂和钠[27].

图8 和图9 是客体在积分差值等于0 时的通量结果.图8(a)是截断角2 mrad 时铜板的通量分布, 优化前系统中的通量值与理想系统中的通量值在边缘处相差(通量差值)最大, 在 ± 49 mm 处二者相差3.7%, 而优化后的通量差值是0.5%.图8(b)是截断角为3.5 mrad 时的通量分布, 在 ± 49 mm 处,优化前后的通量差值分别是1.3%和0.1%.图9(a)是截断角为2 mrad 时同心球客体的通量分布, 在−1 mm处, 优化前后的通量差值分别是2.0%和1.1%.图9(b)是截断角为3.5 mrad 时同心球客体的通量分布, 在 − 1 mm 处, 优化前后的通量差值分别是0.9%和0.2%.

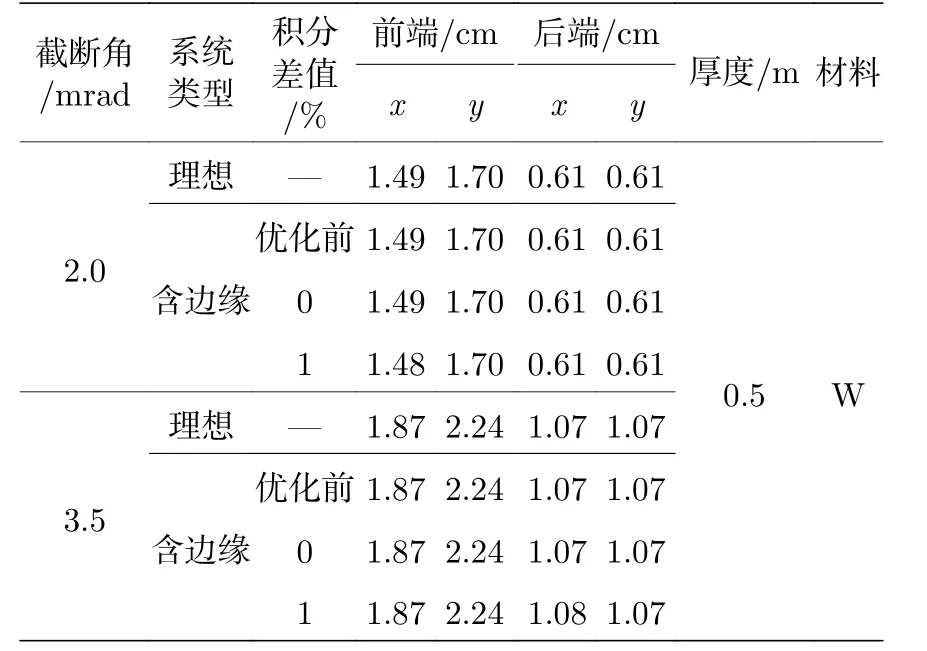
表3 准直器孔径参数Table 3.Aperture parameters of the angle-cut collimator.

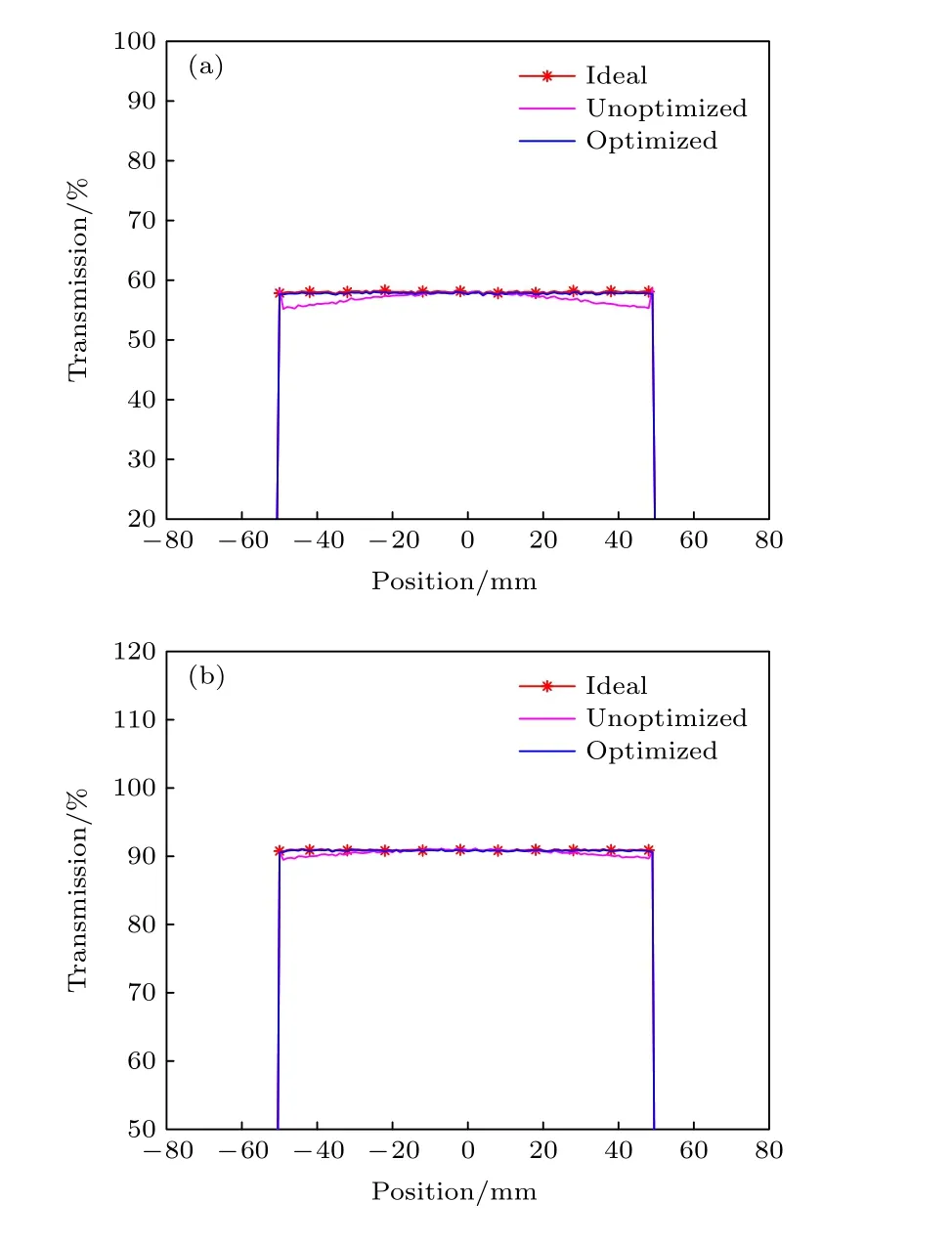
图8 积分差值为0 时质子通过铜板的通量分布 (a) 2.0 mrad;(b) 3.5 mradFig.8.Flux distribution after passing the round copper plate while the integral difference is 0: (a) 2.0 mrad; (b) 3.5 mrad.

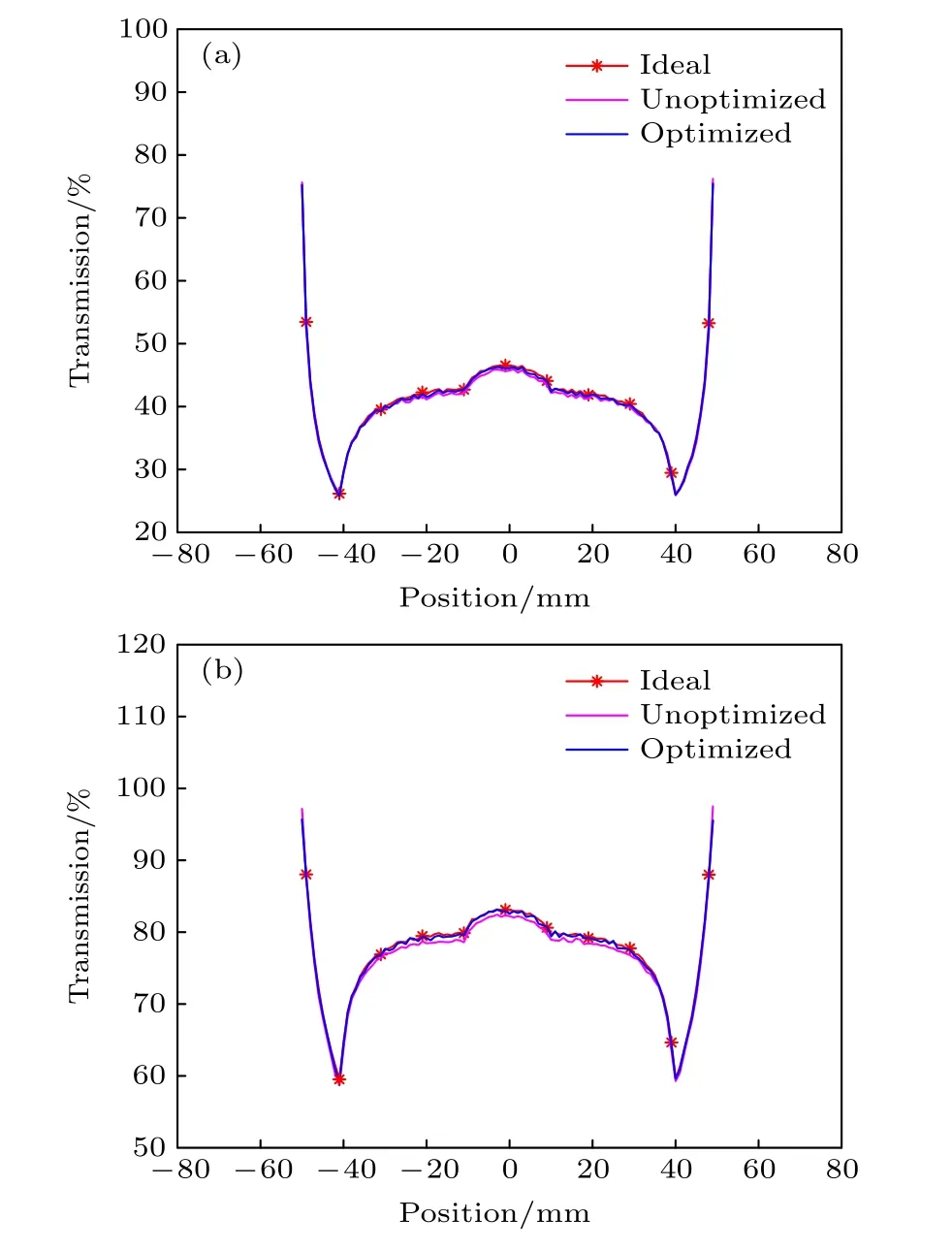
图9 积分差值等于0 时质子通过同心球的通量分布(a) 2.0 mrad; (b) 3.5 mradFig.9.Flux distribution after passing the concentric spheres while the integral difference is 0: (a) 2.0 mrad; (b) 3.5 mrad.

图10 和图11 是客体在积分差值等于1%时的通量结果.图10(a)是截断角为2 mrad 时铜板的通量分布, 在 ± 49 mm 处, 优化前后的通量差值分别是38.6%和0.1%.图10(b)是截断角为3.5 mrad时的通量分布, 在 ± 49 mm 处, 优化前后的通量差值分别是23.9%和0.1%.图11(a)是截断角2 mrad时同心球客体的通量分布, 在 ± 34 mm 处, 优化前后的通量差值分别是9.3%和0.5%.图11(b)是截断角3.5 mrad 时同心球客体的通量分布, 在±34 mm处, 优化前后的通量差值分别是8.1%和0.3%.

综上, 优化前的通量值与理想的通量值均有一定差异, 并且当积分差值为1%时, 二者相差更大,使用优化后的成像系统减小了通量值差异.因此,可以通过优化系统参数来改善成像系统的性能, 从而减小通量误差.

图10 积分差值等于1%时质子通过铜板的通量分布 (a) 2.0 mrad; (b) 3.5 mradFig.10.Flux distribution after passing the round copper plate while the integral difference is 1%: (a) 2.0 mrad; (b) 3.5 mrad.

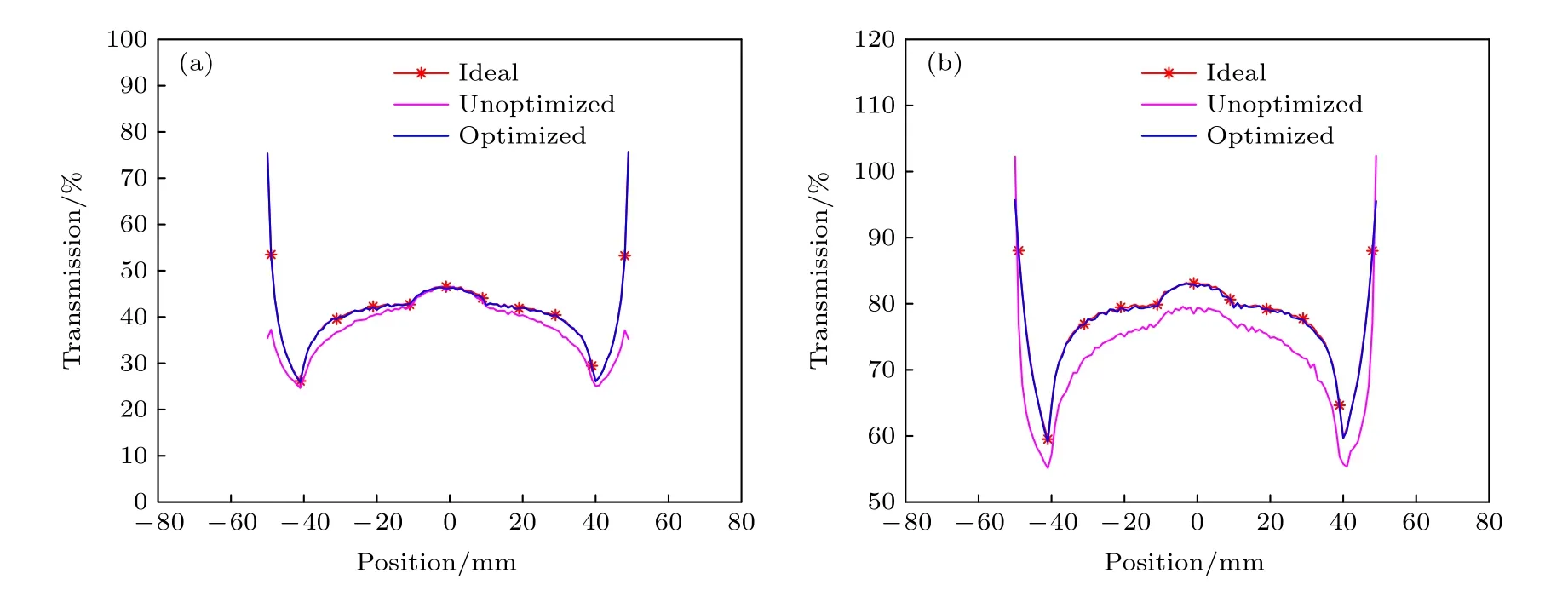
图11 积分差值等于1%时质子通过同心球的通量分布 (a) 2.0 mrad; (b) 3.5 mradFig.11.Flux distribution after passing the concentric spheres while the integral difference is 1%: (a) 2.0 mrad; (b) 3.5 mrad.

5 结 论

通过对磁透镜边缘场的研究, 给出了含边缘场时的质子成像系统的优化方法.利用1.6 GeV 成像系统进行了数值模拟, 并分析了含边缘场时对准直器孔径及质子通量的影响规律.结果表明, 优化后成像系统减小了质子通量误差.进一步研究了梯度积分差值与传输矩阵的关系, 当积分差值在10–2量级时, 发现二者呈线性关系, 并且传输矩阵的改变量与积分差值在同一量级, 因此对准直孔径参数的改变亦在10–2量级.