基于人工神经网络和粒子群优化的初期雨水调蓄池设计方法研究

何胜男，陈文学，刘 燕，穆祥鹏

（1.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038；2.中国电建集团河南省电力勘测设计院有限公司，河南郑州 450016）

1 研究背景

根据中国生态环境部2014—2018年中国生态环境状况公报［1-2］，从2014年至2018年水体劣Ⅴ类占比从9%降至6.7%，随着生态文明建设国家战略的推进，大部分的点源污染得到了控制，非点源污染控制成为当前水环境治理的重点和难点。与其他非点源污染相比，城市地表径流污染是城市水环境的主要污染源之一［3］，随着城市化的加速发展，城市地表径流污染对水环境污染的贡献将不容小觑。

美国早在1975年开始研究地表径流污染控制［4］，中国始于1992年［5］。欧美等国通过地表径流污染控制研究，提出了许多管理和控制策略，如美国在1972年首次提出的最佳管理措施（Best Management Practices，BMP）［6］，英国的可持续城市排水系统（Sustainable Urban Drainage System，SUDS）［7］，澳大利亚的“水敏感性城市设计”（Water Sensitive Urban Design，WSUD）［8］，美国的“可持续基础设施”（Sustainable Infrastructure，SI），1990年代美国提出的低影响开发（Low Impact Development，LID）［9-10］，瑞典、德国、荷兰等国发展的生态排水系统（Ecological Drainage System），中国也于2013年提出了海绵城市建设等。这些方法为非点源污染进行治理，尤其是对城市水环境治理奠定了基础。但对于中国大多数建筑密集的老城区而言，采用LID、SUDS等方法，时间长、造价高，施工难度也较大，修建初期雨水调蓄池设施是解决雨水径流污染既快速、又直接的方法。

目前，初期雨水调蓄池一般采用经验方法设计，例如美国的1英寸法、英国的12～15 mm［11］、中国的城市屋面2～3 mm、路面7～8 mm、降雨量4～8 mm［12］等。经验方法仅考虑初期雨水截留量大小，与研究区域下垫面条件无关。按照该方法设计的初期雨水调蓄池，对于不同的地区，尤其是对于平原城市，地势较缓，汇流速度较慢，污染物携带峰值量较晚出现，其截污效果可能差异甚大。影响地表径流污染物累积特性的因素复杂，主要包括城市的地形、地貌、雨量、雨强、降雨前的干旱天数、交通量、土地利用性质等。因此，为了提高初期雨水调蓄池的截污效果，初期雨水调蓄池的设计，应考虑地表径流污染物的累积特性以及城区的实际情况，如可征用的土地面积和城市污水处理厂的处理规模等。因此，初期雨水调蓄池的设计本质上是约束优化问题，即在满足调蓄池容积约束条件下，实现截污量最大。

本文以中国平原城市某县城城区黑臭水体整治项目为背景，以所有调蓄池的总截污量最大为目标，提出了初期雨水调蓄池容积的优化方法。首先利用SWMM（Storm Water Management Model）模型模拟分析地表径流污染物累积特性，再利用人工神经网络训练出各调蓄池不同截污率与对应总截污量之间的非线性高精度近似数学模型；以调蓄池总截污量最大为优化目标，以污水处理厂处理规模和可用征地为约束条件，采用粒子群优化算法优化各调蓄池的截污率；结合各调蓄池截污率与径流量累积量之间的关系，得出各调蓄池的设计容积，并与国内常用设计方法进行对比分析。

2 优化方法

初期雨水调蓄池的设计需要考虑：（1）地表径流污染物的累积特性。分析研究区的地表径流累积特性，为确定合理的截污率提供科学依据；（2）可用征地和污水处理厂处理规模。根据可用征地面积和污水处理厂的处理规模，可确定调蓄池的布局和最大截污量；（3）寻优方法的选择。考虑排水管网的布置和污水处理厂的分布情况，通常会设置多个初期雨水调蓄池。当仅设置一个调蓄池时，利用多项式拟合可以得到调蓄池截污率与总截污量之间的函数关系，计算函数的最小值即得到最优截污率。但随着调蓄池数量的增加，拟合难度增加，寻优计算的难度也相应增加。为此，本文利用人工神经网络方法得到各调蓄池截污率与总截污量之间的非线性数学模型，利用粒子群优化算法，以总截污量最大为目标进行寻优。

2.1 污染物累积特性一般采用数学模型定量研究调蓄池对应汇水区的污染物累积特性。常用的城市非点源污染负荷的模型有SWMM［13］、STORM［14］、DR3M-QUAL［15］、SLAMM［16］、HydroWorks［17］、HSPF［18］、MOUSE［19-20］等。作为一款开源软件，SWMM 提供4种污染物累积模型和3种冲刷模型，可模拟出水口污染物变化，能考虑单次降雨和长序列降雨，且能与其他软件较好地衔接，因此，得到了广泛应用［21］。本文将利用SWMM模型分析地表径流污染物累积特性。

调蓄池的截污量与地表径流总污染量之比称之为调蓄池的截污率。假定研究区设置n个调蓄池，第i调蓄池对应汇水区包含Ni个排水口，地表径流时间为T（含退水时间），t是地表径流的截流时间。根据SWMM模型模拟结果，可以得到第i个调蓄池对应第j个排水口地表径流过程qi,j(τ)；第i个调蓄池对应第j个排水口地表径流污染物含量ci,j(τ)；各调蓄池累计总量为Mi,max，污染物累计总量计算见式（1）；第i个调蓄池截污率，计算见式（2）；根据地表径流过程，计算调蓄池的容积，见式（3）。

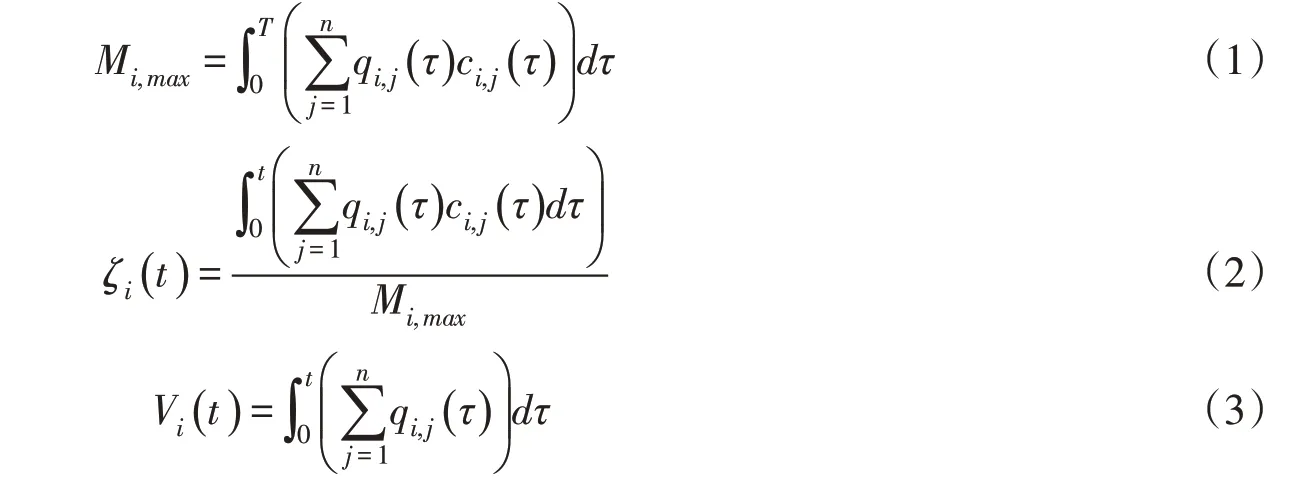
2.2 人工神经网络人工神经网络（Artificial Neural Networks，ANN）［22］是通过设置输入层、隐藏层和输出层，并结合激励函数，建立输入和输出变量之间的非线性关系，根据计算值和真实值之间的误差进行优化，然后通过反向传递，进而改变模型方程权重，如此反复训练，可以得到一组高精度非线性近似数学模型。单层隐藏层人工神经网络总表达式见式（4）。激励函数采用ReLU 函数，见式（5）［23］，本文利用人工神经网络模型训练调蓄池截污率与对应总截污量之间的非线性数学模型：

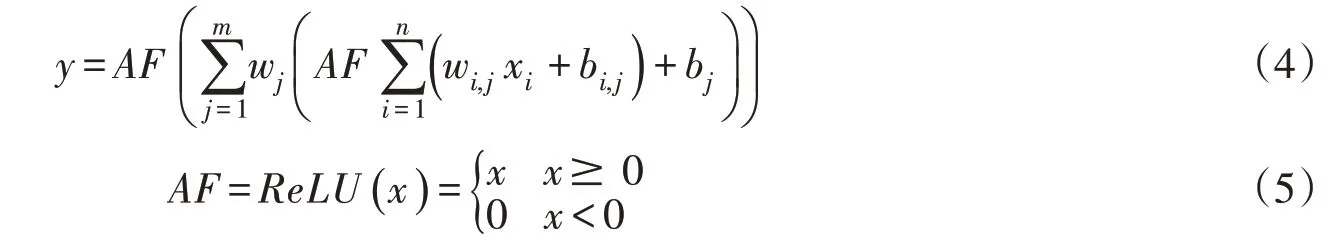
式中：y为输出层；x为输入层；AF为激励函数；xi为输入层变量；wi,j、wj为权重；bi,j、bj为偏置；i为变量个数；j为神经元个数。

为了提高人工神经网络的迭代收敛速度，采用变学习率技术，即指数衰减学习率，计算见式（6），随着迭代次数的增加逐步减小学习率，保证模型训练后期更加稳定［24］。为防止训练时出现过拟合现象，采用L2正则化技术，即在原损失函数上加一个惩罚项，见式（7）［25］。

式中：Lr0为学习率初始值；n为当前训练轮数； Δn为学习率变化间隔（步数）；Lrd为学习率衰减值。

式中：C0为初始损失函数；w为权重；λ为正则化参数。

数据样本的数量和样本代表性影响函数拟合的精度。通常样本数量越多，模型预测精度越高。但是实际样本数量应根据变量个数、采样点范围和客观条件等确定。为提高样本数据的代表性，选择拉丁超立方抽样（Latin Hypercube Sampling）方法。拉丁超立方抽样方法是由三位科学家McKay、Beckman和Conover提出的分层随机抽样方法［26］，其优势是划分概率相等的间隔，在该间隔中选取一个样本点，不需要更多维度的样本就可以达到相同的效果［27］。

2.3 粒子群优化算法粒子群优化算法（Particle Swarm Optimization，PSO）［28］是由Kennedy和Eberhart首先提出的一种全局随机搜索算法。它首先初始化一组粒子（可行解），各个粒子根据自身最优解和群体最优解来更新个体的速度和位置，直至达到最大迭代次数或者满足预设精度为止。为了更好的控制种群在全局范围内和局部的搜索和寻优能力，本文采用Shi等提出带惯性权重的PSO算法［29］，计算见式（8）和式（9），其中惯性权重w和学习因子c均进行线性降低优化改进，分别见式（10）和式（11）。

式中：v、x为粒子的速度和位置；d=1，2，…，n，n为搜素空间的维数；i=1，2，…，m，m为种群规模；t为当前进化代数；c1、c2为学习因子；w为惯性因子；r1、r2为［0，1］内的随机数；pid为粒子历史最优位置；pgd为全局粒子最优位置粒子；速度v∈[]-vmax，vmax，其中vmax为粒子的最大速度。

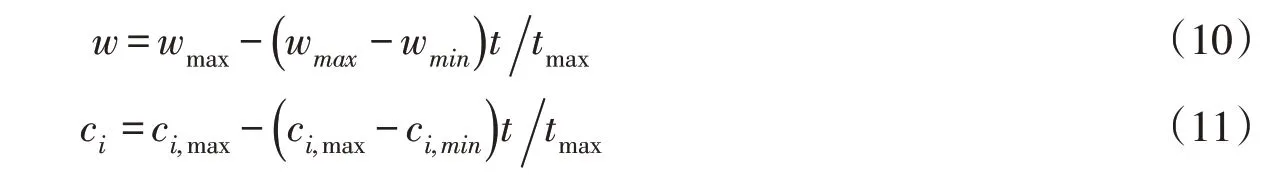
式中：wmax、wmin分别为最大、最小权重；ci,max、ci,min分别为第i个最大、最小学习因子；tmax为迭代次数；t为当前迭代次数。

2.4 优化模型初期雨水调蓄池的优化模型为：

调蓄池总截污量的计算公式为：

式中：Mi,max为第i个调蓄池对应汇水区的污染物最大累计量；ζi为第i个调蓄池对应的截污率，其中ζ≤ζi,max。

调蓄池总容积的计算公式为：

粒子群优化算法没有处理约束条件的机制，本文采用罚函数法［30］，即将约束函数与目标函数组合成新的目标函数，将带有约束条件的优化问题转化为无约束的优化问题。具体计算公式为：

2.5 调蓄池优化方法初期雨水调蓄池的优化方法如下：（1）建立SWMM 城市径流污染模型，分析研究区各调蓄池对应汇水区的污染物累积特性；（2）根据当地经济、占地、对应设备以及污水处理厂处理规模等客观条件，确定各调蓄池实际最大容积Vi,max，将约束条件转化为各调蓄池实际最大截污率ζi,max；（3）利用拉丁超立方抽样方法在[]0，ζi,max内构建数据样本，结合总截污量模型方程，计算每组截污率组合对应的总截污量，最终形成m组各调蓄池不同截污率和对应总截污量的数据样本；（4）利用人工神经网络模型对数据样本进行训练，得到一个高精度非线性的截污率与总截污量之间的数学模型；（5）以为优化目标，采用粒子群优化算法计算各调蓄池的优化截污率；（6）根据优化截污率，计算得到各调蓄池优化截污率对应的时间，计算各调蓄池的最适容积。

3 实例

3.1 研究区概况以中国平原城市某县城城区为例，城区拟设计9座截污调蓄池，研究区的总面积是43.646 km2，地势平缓，西北高，东南低，地面高程平均海拔26.5～33.5 m，地面自然坡降为1/9000。城区内河流水质差，大部分为Ⅴ类水，其主要污染物为化学需氧量COD（Chemical Oxygen Demand）。

3.2 水质模型以SWMM为平台，对研究区和排水系统进行概化，概化后得到690个子汇水区，总面积为42.135km2，管道876根，节点876个，出水口174个。研究区各要素的概化图及子汇水区分区情况如图1 所示。各子汇水区的不透水率和坡度利用地形资料和遥感影像借助ArcGIS 计算得到。Routing Model选择Dynamic Wave and Allow Ponding，Infiltration Model选择Horton模型，汇水区宽度系数、不透水区糙率、透水区糙率、不透水区洼蓄量、透水区洼蓄量、最大入渗率、最小入渗率、衰减常数、晴天时间分别取0.8、0.013、0.17、1、3、76.2、3.81、2、7［31］。

本文选取COD 作为研究区的降雨径流污染指标。研究区的土地利用分为路面、屋面和绿地，对应各土地的不同污染物累积参数和冲刷参数不同，根据SWMM 手册［32］和相关文献［33-34］得到污染物累积和冲刷所需要的参数，见表1。

图1 研究区概化分布

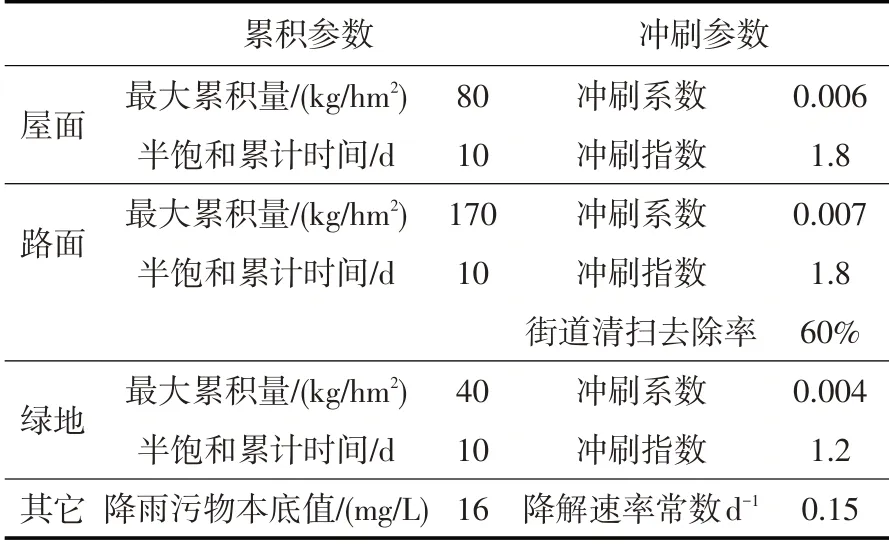
表1 污染物累积和冲刷参数

降雨量和雨强的大小直接影响着排口处污染物的累积情况。考虑到研究区排水管网的设计标准是5年一遇，本文以设计暴雨5年一遇作为初雨调蓄池的设计标准。设计暴雨雨型选择芝加哥雨型［35］，雨峰系数取0.4，本文采用当地暴雨强度公式：

式中：q为暴雨强度，L/s·hm2；t为降雨历时，min；P为暴雨重现期，a。

3.3 污染物特性地表径流模型模拟时间24 h（包含退水时间），前期干旱时间选择10 d，计算步长为5 s。模拟出研究区各排口污染物COD随时间过程线，根据各调蓄池对应汇水范围，计算得到各调蓄池对应汇水区COD累积过程线，见图2。

从图2可见，研究区地表径流污染物具有初期累积速度较慢，中期累积速度较快，后期缓慢增加的特征。受子汇水区面积和下垫面的影响，各调蓄池对应汇水区污染物累计总量差异较大。因此，在设计初期雨水调蓄池时，必须要考虑污染物的累积特性，尽可能地截留较多的污染物，以减轻非点源污染对城市水环境的影响。

3.3.1 污染物累积总量 结合SWMM计算结果，各调蓄池污染物累计总量为Mi,max，见表2。

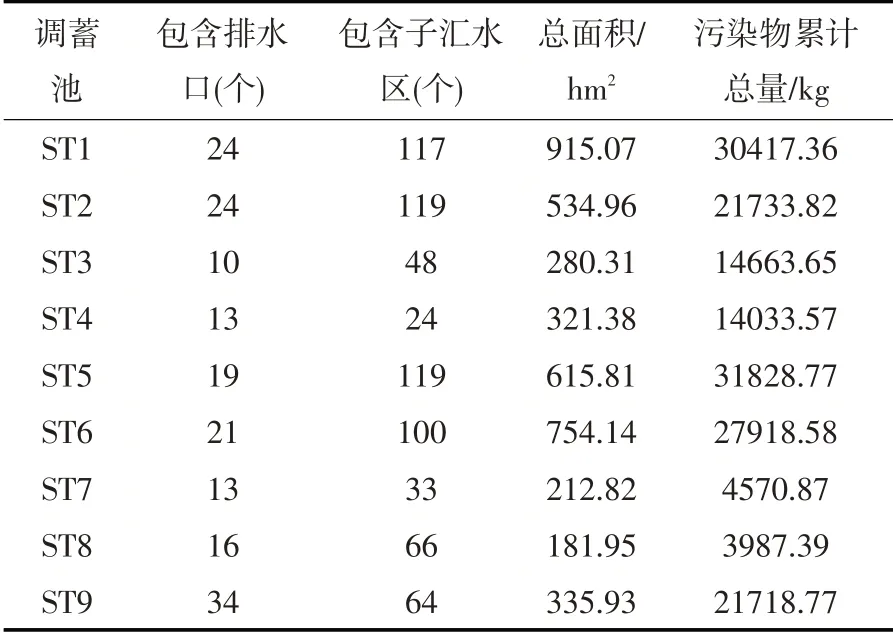
表2 各调蓄池污染物累计总量

图2 不同汇水区COD前期累积过程线

3.3.2 各调蓄池截污率 以调蓄池ST1 为例，调蓄池对应汇水区污染物COD 截污率过程线如图3 所示，不同截污率对应的截留径流量曲线如图4所示。

3.3.3 截污率与径流量拟合公式 为了便于计算，对各调蓄池污率和径流量的关系曲线进行拟合，研究发现，采用Gaussian 曲线可以很好地拟合截污率与径流量之间的关系，拟合曲线的相关系数R2大于0.98。具体计算公式为：

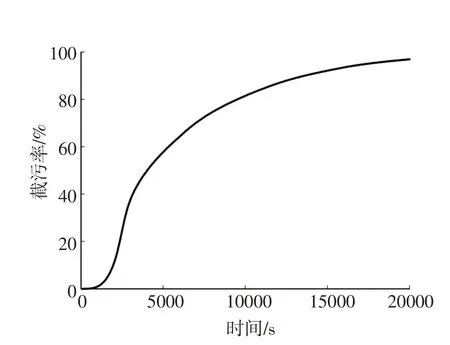
图3 调蓄池ST1对应汇水区截污率过程线

图4 调蓄池ST1对应汇水区截污率与径流量关系曲线

式中：V (ζ)为径流量；N为拟合函数的项数；ai、bi和ci均为系数。

3.4 优化结果根据研究区征地情况，各调蓄池的建设最大容积为5万m3；根据研究区污水处理厂的处理规模，调蓄池的总容积不能超过18万m3。根据各调蓄池汇水区的污染物累积过程线和对应径流量过程线，计算出9 个调蓄池的最大截污率ζi,max分别为34.13%、45.68%、62.93%、46.38 %、36.73%、34.64%、75.28%、74.47%和45.77%。

研究区设置9个调蓄池，若在截污率范围内分别取10个采样点，则数据样本高达109。样本数量迅速增加，计算效率将显著降低。结合作者的计算机硬件条件，本文控制数据样本为600万。再利用拉丁超立方抽样方法对各调蓄池按照截污率在[]0，ζi,max内抽样，生成600万组各调蓄池不同截污率数据组合，通过式（1）和（15），计算每行不同截污率组合对应的总截污量，最终形成600万行、10列的数据样本组，其中前九列是9个调蓄池分别对应的截污率，第10列是对应的总截污量。

借助spyder（python 3.5）平台，调用tensorflow 模块，搭建人工神经网络模型，数据样本组分为训练组和验证组，训练组取590万组，验证组取10万组。为加快模型训练的收敛速度，初始学习率取0.1，学习率衰减率取0.99，改变学习率时的步数取50。输入层为训练组数据的前九列，设置一层隐藏层，隐藏层神经元个数取40，输出层为对应的计算总截污量，通过与训练组数据的第10列进行误差计算，并根据学习率学习误差，通过反向传递，更改人工神经网络中的权重，并重新按照新的权重进行训练，总模拟步数为3000，训练各调蓄池截污率与对应总截污量之间的数学模型。。

利用已训练出的数学模型，通过验证组数据，预测对应的总截污量，与验证组实际总截污量进行对比。采用均方误差MSE（Mean Square Error）、均方根误差RMSE（Root Mean Square Error）和平均绝对百分比误差MAPE（Mean Absolute Percentage Error）评价模型。通过计算MSE=0.0017，RMSE=0.041，MAPE=8.4%，验证精度高。

为了加强全域的搜索能力，粒子群优化过程中，wmax=0.9，wmin=0.4，ci,max=2.5，ci,min=0.5，tmax=4000，种群规模为30。优化调蓄池的结果，见表3。

表3 优化调蓄池结果

从表3可以看出，各调蓄池容积均小于5万m3，所有调蓄池总容积为17.98万m3，满足总容积的约束，并接近18万m3，充分利用了可用容积，总截污量为44349.14 kg，全域截污率为25.93%。

<1)，且各件产品是否为不合格品相互独立．

3.5 规范设计设计初期雨水调蓄池通常根据《室外排水设计规范》（GB 50014-2006）［12］进行设计，计算公式如下：

式中：V为调蓄池有效容积，m3；D为调蓄量，按降雨量计，可取4～8 mm，本文取5 mm；F为汇水面积，hm2；ψ是径流系数，本文取0.51；β安全系数，可取1.1～1.5，本文取1.2。

根据经验设计方法得到的计算结果见表4。

表4 设计调蓄池结果

3.6 对比分析本文提出的优化方法简称为“优化法”，规范设计方法简称为“规范法”，二者计算结果比较见图5。

从图5中可以看出，（1）通过相关性分析，“优化法”设计的调蓄池的截污量和总截污量之间的相关系数为0.78，“规范法”设计的调蓄池的截污量和总截污量之间的相关系数为0.34。因此，与规范设计方法相比，优化方法更能体现地表径流的污染物累积特性。

（2）“规范法”所需资料少，方便快捷，但该方法对不同汇水区采用相同的调蓄量计算公式，没有考虑不同子汇水区地表特性和地表径流污染量的差异。以ST5为例，该调蓄池对应的汇水区位于老城区，不透水面积比较大，因此，污染物累积量最大。利用规范法设计的调蓄池，容积仅有0.98万m3，截污率仅有5.1%，截污效果差，而“优化法”得到的调蓄池容积为4.97万m3，截污率为36.7%，截污效果优于规范设计法。

（3）规范设计方法仅与子汇水区的面积有关，优化设计方法则与子汇水区面积、污染物累积过程、污染物累积总量及调蓄池的约束条件有关，因此，从计算结果看，尽管会出现部分调蓄池优化结果的截污量小于规范方法，但是，从研究区域的总截污量来看，优化方法大于规范设计法。

（4）比较表3和表4可见，“规范法”得到的调蓄池总容积为12.71万m3，截污总量26 590.06 kg，“优化法”得到的调蓄池总容积为17.98万m3，截污量44 349.14 kg，与规范方法相比，优化方法总容积增加了41.5%，但截污量增加了66.79%。因此，相比较而言，采用优化方法设计的调蓄池提高了土地的利用效率。

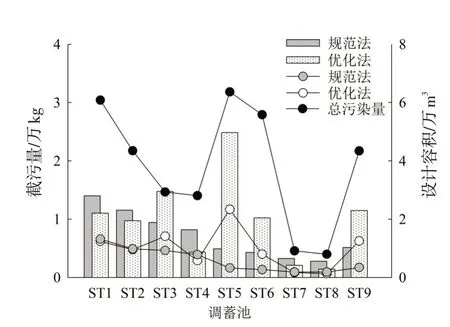
图5 优化法与规范法结果对比

4 结论

本文以中国平原城市某县城城区黑臭水体整治项目为背景，提出了一种满足污水处理厂处理规模和土地利用规模等约束条件下的初期雨水调蓄池优化设计方法，研究表明，本文提出的优化设计方法设计，能在满足实际占地和污水处理厂处理规模下实现截污效果最大化，采用本方法设计的调蓄池在土地使用率和截污效果方面均优于规范设计法。该方法科学、高效和适用范围广，可为城市初期雨水调蓄池设计提供技术支撑。