基于遗传算法和Python 多处理器并行计算的二阶热传导方程初边值问题数值解法

李丙春

（喀什大学 计算机科学与技术学院，新疆 喀什 844000）

0 引言

大多数科学和工程领域中的偏微分方程很难求其解析解，甚至没有解析解，因此利用计算机编程实现偏微分方程的数值求解就显得十分重要.文献[1]针对一类非线性双曲型偏微分方程，构造了混合有限元两层网格算法.文献[2]对含有非线性扩散项和非线性源项的一般形式的热传导方程，通过在演化方程中增加两个关于源项分布函数的微分算子，构造新的格子Boltzmann 求解模型.文献[3]针对非线性偏微分方程初边值问题，利用逐层优化的方法进行数值求解.文献[4]利用NumPy 多维数组和通用函数设计实现了LBM 流场数据结构和典型计算内核，通过一系列性能优化并对LBM 边界处理算法进行重构，大幅提升了Python 的计算效率.

本文针对二阶热传导非线性偏微分方程，利用离散差分格式，将方程的初、边值作为初始条件，沿着时间方向t 逐列，再沿空间方向x逐行计算.在计算的过程中，把当前需要计算的点作为优化参数，调用遗传算法模块进行参数寻优，进化结束后用最优参数值作为当前结点的函数值.同时，为了加快计算速度，使用了Python 中的多处理器模块进行并行计算.

1 带初边值问题的非线性偏微分方程差分格式

设需要求解的带初边值的二阶非线性偏微分方程形式如下：

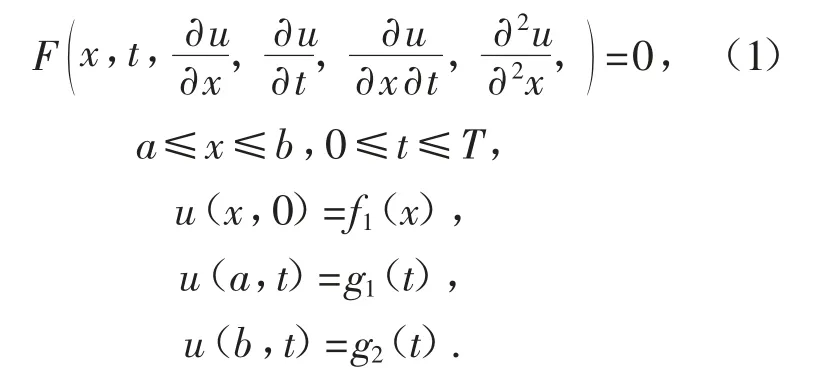
对求解区域a≤x≤b，0≤t≤T 进行网格化处理，取空间方向x 的步长为Δx，时间方向t的步长为Δt，如图1 所示.

网格中第一行和最后一行分别是x=a 和x=b 时u 的值，第一列是t=0 时u 的值，根据初边值条件，它们都是已知的.求解时按照先逐j列后逐行的顺序进行，因此，在求解第列时，前一列即j-1 列已知计算出来了，可作为已知条件使用.

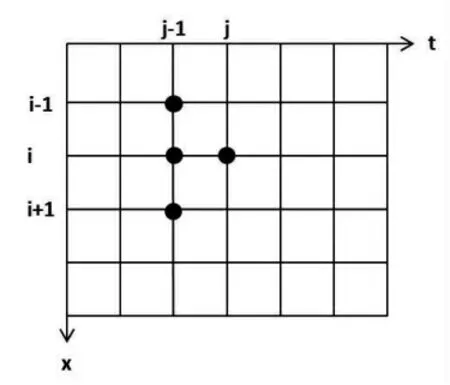
图1 求解区域网格化

数值求解非线性偏微分方程（1）时，按照图1 的模板结构，可采用如下形式的偏导数差分格式：

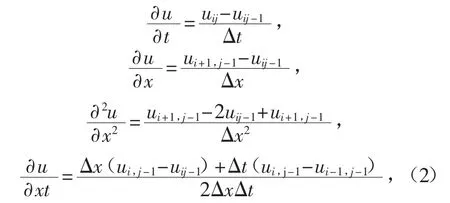
将式（2）代入非线性偏微分方程（1），得到关于差分格式的偏微分方程

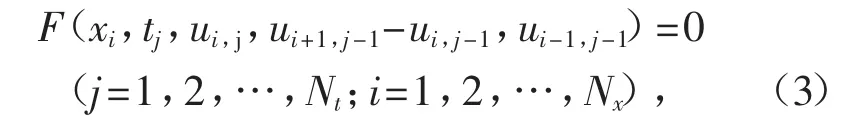
其中，下标i 和j 都从0 开始，Nt和Nx分别是时间方向和空间方向分割的点数.

2 带初边值问题的非线性偏微分方程逐点优化算法

由非线性偏微分方程差分格式（3）表明，如果ui，j,ui+1，j-1,ui，j-1和ui-1，j-1是偏微分方程的精确解，则（3）式应该完全成立.但这里是数值解，误差一定会存在，因此（3）式不会完全成立.但如果（3）式的左端足够小，趋近于0 的程度非常好，则对偏微分方程数值解来说是可以接受的.

按照时间t 的方向逐层求解的思路，式（3）中 的ui+1，j-1，ui，j-1和ui-1，j-1是前一轮已经求解出来的，ui，j是未知的，需要本次求解.极小化目标函数

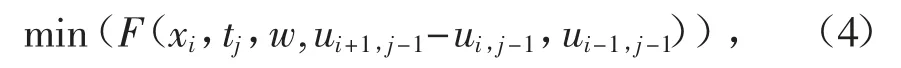
这是一个单变量优化问题，优化结束以后，令

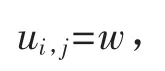
即以优化算法结束后得到的优化变量值作为当前网格点的值.算法形式描述如下：

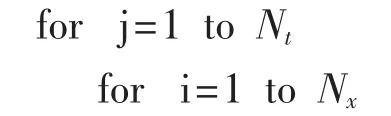
调用遗传算法ga 求解目标函数（4），优化变量w

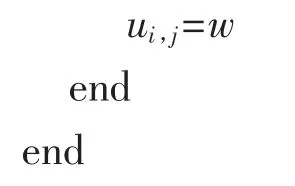
本算法对网格中的每个点（除初边值条件已知的第一列、第一行和最后一行以外） 逐点调用遗传算法进行优化求解，后面的实例可以发现，能够获得精度很高的数值解.

3 Python 多处理器并行计算

上述通过逐点调用遗传算法优化数值求解偏微分方程函数值的方法可以取得令人满意的结果，算法的实现也较为容易.但因为是逐点优化计算，而遗传优化算法是一种随机搜索算法，其本身的时间消耗较大，导致该算法运行时间较长.考虑到现在使用的计算机一般都是多核处理器，基本都可以达到4 核，很多情况下系统运行时只有一个核心在工作，其它核心处于闲置状态，如果能够把多个核心都利用起来并行计算，肯定可以加快运算速度.本问题是一个计算密集型任务，正好可以体现多处理器并行计算的优势.本文在Python 环境下使用多处理器进行并行运算，形式描述如下：

（1） 定义函数fun

定义目标函数objfun；

调用遗传算法ga 对目标函数objfun 进行优化；

返回最优变量w.

（2） 主函数使用多处理器并行计算，假设CPU 有4 个核心.

4 实例分析

设某非线性偏微分方程为：

按照差分格式（2），构造如下形式的离散方程作为目标函数：

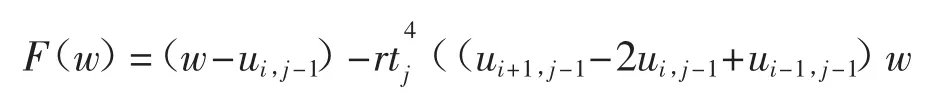
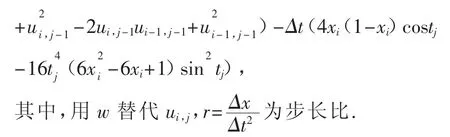
极小化目标安函数F（w），最后取ui，j=w 即可，即

该非线性偏微分方程有精确解

（1） 取Δx=0.05，Δt=0.001，优化计算结束以后，本文算法数值解与精确解部分结果比对如表1 所示.

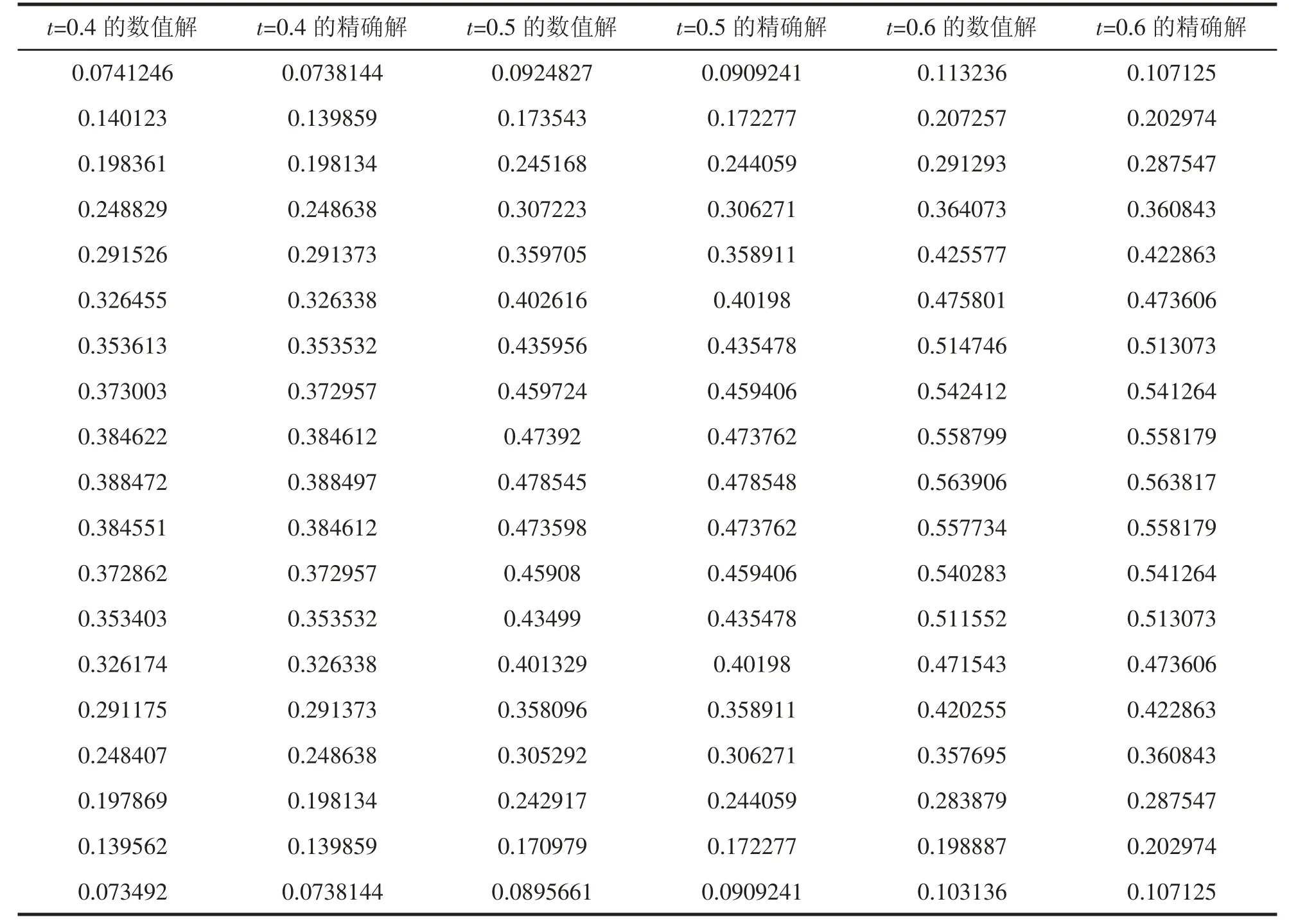
表1 t=t0 时数值解与精确解部分结果对比

数值解与精确解绘制的三维曲面图如图2所示.

t=0.4 时，数值解函数值与精确解函数值曲线如图3 所示，其中黑色小圆点是偏微分方程的精确解.

从图2 和图3 可以看出，利用本文方法得到的数值解可以很好地逼近偏微分方程的精确解.

（2） 误差分析.

计算值与精确值的最大绝对误差为0.0573 1063826562638，平均绝对误差为0.00196653218 11486165，均方误差MSE 为2.34914289567480 68e-05.

（3） 单核计算与多核计算比较.

使用单核计算，需要耗时16824 秒，开启4核并行计算，消耗的时间为4748 秒，速度可以提升3.5 倍左右，加速的效果还是很明显的.

（4） 总时间长度T 对计算精度的影响.

实验发现，总的时间长度T 对计算精度有影响，当T=0.5 时，计算值与精确值的最大绝对误差为0.0015586254247764858，平均绝对误差为5.9936176114377825e-05，均方误差MSE为4.9188825689194596e-08.与T=0.8 时的计算精度相比，有很大的提高.

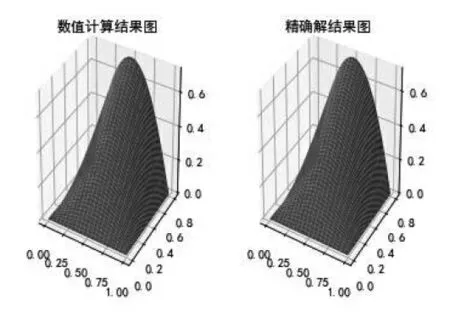
图2 数值解与精确解三维结果图

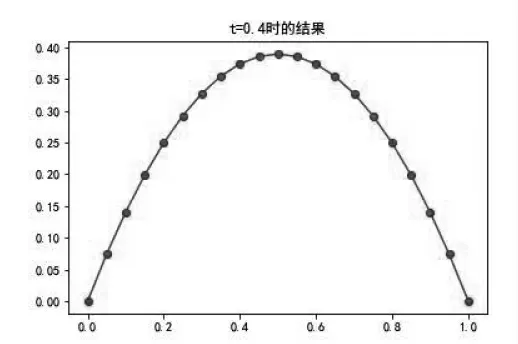
图3 t=0.4 时数值解与精确解对比

总时间长度T=0.5 比T=0.8 的计算精度高几个数量级，其原因是由于采用了逐层优化计算，每个点的计算值本身是近似结果，具有一定的误差，这些误差是会向后传播的，因此随着时间的向后推移，误差会逐渐增大，导致计算精度会逐渐下降.