汽车空调鼓风机自适应控制算法的研究

罗成志,沈 勇，卢忠岳，王文斌，张 鑫

(1.云南民族大学 电气信息工程学院, 云南 昆明 650000；2.华南农业大学 工程学院, 广东 广州 510000)

随着环境保护意识的不断提高，汽车车内空调控制系统的这一复杂的热环境系统，能改善车内空气的温湿度条件，在保证乘员乘车的舒适度的同时尽可能减少能耗，来达到节能减排的目的.汽车空调系统的主要核心部件鼓风机，其工作性能是直接衡量汽车空调好坏的重要指标之一.

随着汽车空调控制器的不断更新迭代，鼓风机的控制也从手动控制发展到自动控制，但现阶段鼓风机的控制更主要靠汽车内部的MCU.国内众多研究人员，就鼓风机的控制进行了深入的研究，主要有微机控制、PID控制、模糊PID控制等.如欧艳华等[1]在PID控制原理的基础上提出了1种PID控制的车载空调控制系统；李俊等[2]采用模糊控制来实现对汽车的空调系统的温度控制.尽管国内众多研究人员对鼓风机进行深入研究，但在鼓风机的控制方面仍存在不能使能耗最小化的缺点.

文中主要研究的汽车自动空调的鼓风机，主要运行受车内外温度和湿度、散热等多因素影响.考虑到空调控制系统的复杂性和人体的舒适性，将模糊控制器引入传统的PID控制中，以在Matlab平台上建立Simulink模型，再通过应用改进PSO算法来找到PID的3个参数的最优值，并将最合适的参数作为PID控制器的输入.空调在启动后使鼓风机能在最短的时间内进入正常工作状态，以提高空调控制系统的控制效果，改善车内环境的舒适度以及节约能源的消耗.

1 汽车空调控制系统

在汽车空调系统中，空调的出风量与鼓风机的转速有关.在车厢内密闭的环境下，要使汽车空调在启动之后在尽可能短的时间内达到稳定的状态，对改善车内环境起着至关重要的作用.而鼓风机的控制与车厢内外的温湿度、风速等环境密切相关.通过这些参数的输入，空调控制器通过控制策略控制鼓风机的转速来控制送风量，转速越快，风量越大，制冷输出量越大.传统的空调控制器采用PID控制算法，而自动空调的鼓风机是在车况不确定以及温湿度、空气流速、散热等复杂的条件下经过算法控制的.因此，在环境变量众多且影响因素不确定的情况下，将模糊控制器引入传统的PID控制中.

一般而言，模糊控制是在对前人生产操作经验进行总结后得出的.是基于模糊语言、模糊集理论以及模糊逻辑推理的1种控制思想[1].模糊控制理论对非线性时变系统具有良好的适应性，因其在输入因素多、输入变量不确定的条件下，仍具有精确的数学模型.将PID控制理论与模糊理论相结合形成模糊自适应PID理论.即，在PID控制器中引入模糊控制规则形成模糊PID控制器.其原理图如图1所示：

图1 模糊PID的结构图

鼓风机转速及其控制效果是衡量1个汽车空调性能的标准之一.本文是在模糊控制理论的基础上对汽车空调的鼓风机控制系统的算法进行了深入的研究与实验.在该汽车空调控制系统中，输入量分别是车内实际温度与目标温度的差值e和差值的变化率ec，输出量为PID控制的3个参数Kp、Ki、Kd，为了满足该汽车空调控制系统的需求，需要设计具有双输入、三输出的模糊控制器.再利用模糊规则的原理建立适应此系统的模糊规则，对2个输入量不断的监测，在模糊规则的筛选下对3个参数Kp、Ki、Kd进行实时输出调整，来改善控制系统的控制效果.3个输出的调整公式为：

Kp=Kp0+ΔKp，

(1)

Ki=Ki0+ΔKi，

(2)

Kd=Kd0+ΔKd.

(3)

综合到考虑本文研究的控制系统的特点，兼顾模糊控制规则的稳定性、精确性的基本控制要求.将输入变量的偏差值e和偏差变化率ec以及所要输出的输出变量Kp、Ki、Kd对应的语言变量所代表的模糊集可分为7个类别，一般1个模糊子集对应着1种类别，便有7个子集.即：{NL(负大)，NM(负中)，NS(负小)，Z(零)，PS(正小)，PM(正中)，PL(正大)}，其中，N=Negative，P=Positive，表示变化的方向；L=Large，M=Medium，S=Small，Z=Zero，表示模糊变量的大小程度.由于可能存在失控的现象，为了规避这个可能性，模糊子集就需要对其论域的覆盖率有一定的限制.一般的模糊子集的总数为模糊论域中元素的1/3～1/2,.因此定义，偏差值e和偏差变化率ec的大小分别由这些模糊语言的模糊集合来代表，模糊集合的语言论域的取值范围为[-6，6].由于输入量和输出量均属于控制变量，那么模糊控制器所处理的是模糊量，就需要在精确的控制量和模糊量之间确定两者的转换关系.因此需要将精确量转化为模糊量的模糊化.在本文的研究对象中，采用三角函数的方法，即：

在对隶属函数进行离散化时采用三角函数的方法

根据上述的模糊理论中的模糊规则来制定模糊规则表，如表1所示.模糊规则如下：

If e is NL andecis NL, thenΔKpis PL, ΔKiis NL,Kdis PS；

If e is NL andecis NM, then ΔKpis PL, ΔKiis NL,Kdis NS等若干条规则.

在完成了模糊化之后需要就模糊规则对输入量进行解模糊化，考虑到解模糊化需要将模糊空间论域与精确控制空间一一映射的关系，在本文中采用加权平均法来处理解模糊化的问题，该方法的适应性较强且方法简单，能适应实时性要求较高的系统.设值域为z0，则z0的隶属度函数为μc(z)，则其计算公式为：

(4)

表1 模糊控制规则

根据上述所确定的模糊变量、论域和隶属函数在Matlab平台上对基本参数进行编辑和设定隶属函数曲线.确认具有双输入、三输出的模糊控制器的输入量为E和EC以及输出量为Kp、Ki、Kd.对该输入输出关系的隶属曲线进行编辑.Kp、Ki、Kd的三维规则图可从具有模糊规则的模糊控制器中得出.其中如图2所示为Kp的输出三维图.

图2 Kp参数的模糊规则图

2 改进的粒子群优化算法

2.1 基本粒子群算法原理

粒子群优化算法(particle swarm optimization,PSO)，一种可以适用智能化需求较高的计算机控制技术在1995年被Eberhart和Kennedy提出.其基本原理，是在整个粒子群里，粒子都代表的是可能存在的解，有多少个粒子就可能有多少个解，但是对于方程来说，解的个数是固定的，那么就要求出最优解.因此需要通过这些粒子被优化函数所确定的可能解进行优化分析.根据本文的具体研究课题，在标准的粒子群优化算法的基础上，提出改进粒子群优化算法(PSO).因具有收敛速度快、设置参数少及操作简单是粒子群优化算法的优点，在不同研究领域得到了应用.基本的粒子群算法的更新公式为：

Vid=ωVid+C1random(0,1)(Pid-Xid)+C2random(0,1)(Pgd-Xid).

(5)

其中，ω为非负惯性因子，其全局寻优能力与其值大小相关.C1和C2为粒子的加速常数，其中前者是粒子的个体学习因子，后者是社会学习因子.通常，C1和C2均为常数时能得到较好的解，一般设置为C1=C2=2，取值范围一般是[0,4].random()表示随机数，其分布在[0,1]区间内.其中，Pid表示为第i个变量的体粒子极值的第d维，Pgd则代表全局最优解的第d维.Vid为粒子的速度，由于要在优化过程中确保粒子的寻优迭代的效率，所以粒子的位置和速度都受到了一定的限制.其位置的迭代公式为：

Xid=Xid+Vid.

(6)

粒子群优化求解的迭代步骤如图3：

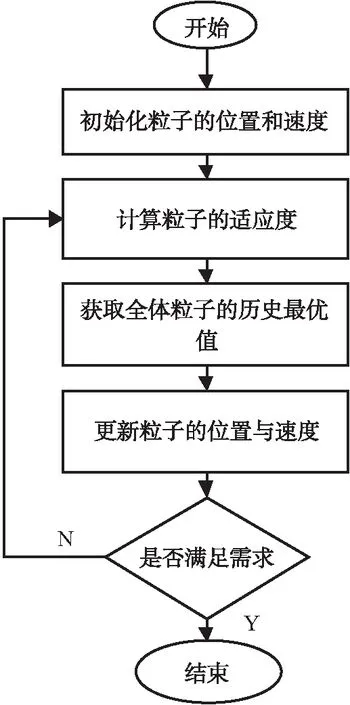
图3 粒子群算法寻优流程图

2.2 粒子群优化算法的改进

由于局部中会出现收敛过早的问题，所以尽管粒子群优化算法的收敛速度很快，但在许多具体的研究应用中仍无法解决大多数问题.而当单个粒子陷入局部最优或者停滞的现象时，大多数情况只能单方面的依靠粒子的合作与竞争，改善此种现象的方法有惯性权重法、死区划分及死区内粒子初始化.

2.2.1 线性惯性权重法

在式(5)中，即标准粒子群算法的公式中，ω为非负惯性因子，美国的Shi和Eberhart研究发现[3]，在基本公式中惯性因子ω的对算法的影响较大，其值与算法的搜索能力成正相关.大量的研究人员对此进行了实验验证，粒子群优化算法要想获得较快的收敛速度，则ω的取值需要在0.8～1.2之间[4].在搜索初期，较大的ω值使粒子在全局搜索能力中显著占优，但是在求解搜索的后期，过大的ω值对局部搜索能力是不利的.因此，需要对算法进行改进，能使ω能随迭代次数线性减小，以达到在较大的区域时PSO仍然可以快速找到最优解的近似位置.而随着ω的逐渐减小，粒子的速度也随着下降，并且开始进行局部精细的搜索.改进后的算法和惯性因子ω的变化公式如下所示：

(7)

(8)

(9)

式中ωmax、ωmin为初始与结束惯性因子.前一时刻的速度与当前速度相互之间的关系受惯性因子的控制.因此其直接影响了粒子在局部以及全局的搜索能力.经过试验证明：Benchmark方程的显著的改善是通过对粒子群算法的改进.但是实际的优化搜索过程无法由ω的线性递减完全反映.另外，粒子群优化算法的实际搜索过程中复杂度很高，并且是非线性的[5].因此，随着迭代次数的增加，该算法的全局搜索上能力不足便无法继续寻找最优解.即，无法求得最优的Kp、Ki、Kd的值.

2.2.2 死区邻域法

汽车空调系统不仅要确保车内的温湿度和空气的流动性，使乘员在车内感受到舒适，还要考虑到节省空调的能耗.在空调能耗得到保障的前提下，利用模糊控制器对输出参数Kp、Ki、Kd寻求最优的值.此方法以局部的极值为中心，将粒子领域的半径划分为死区，将这个区域内的粒子全部初始化，再利用sharing函数排斥进入该区域的其他粒子，该方法可使粒子群的跳跃区域不大，粒子具有更快的收敛速度及更强的收敛性[1].对粒子的迭代进行分析可得，当粒子出现全局或局部最优时便会出现停滞现象，可通过粒子的更新状态进行判断.任意2个粒子之间的最大距离可用来计算每1个粒子与粒子群中其他粒子的距离R.即：

(10)

上式指粒子a到b的绝对距离，当粒子b满足：

(11)

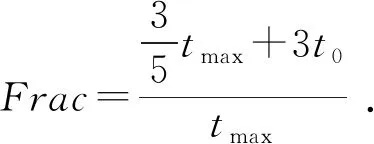
(12)

由上述式子可得改进的PSO算法的全过程，其流程图如图4：

根据本文所述改进PSO算法，在Matlab上编写线性惯性权重与死区划分法相结合的粒子群优化算法的M函数，可以得到较为理想的粒子收敛的记录曲线.如图4所示：

图4 改进的PSO算法流程图

2.3 PSO优化模糊PID参数

经过整定的PID参数ΔKp、ΔKi、ΔKd为粒子群的优化对象，在模糊PID控制器中，对整定的3个参数进行寻优，取得最优值.在原有的模糊PID控制器的整定Kp、Ki、Kd时加入改进的粒子群优化算法，对参数进行寻优.

在量化因子进行调整后，将偏差量e与偏差变化率ec转化为输入量E和EC，并通过模糊控制器与PSO的自适应寻优能在最短的时间内对Kp、Ki、Kd进行寻优，找出Kp、Ki、Kd的最优值，提高系统的响应速度以及精确度，通过Ku的转化为实际的输出值至PID控制器.

3 汽车空调控制算法的建模与仿真

根据本文所述理论以及对PSO算法的改进，在Matlab上分别搭建模糊PID控制系统的Simulink模型以及采用本文上述的改进的PSO算法的m函数，对模型进行仿真分析.图4是在simulink平台上搭建的数学模型，图5为粒子群算法对参数优化后的PID算法结构.

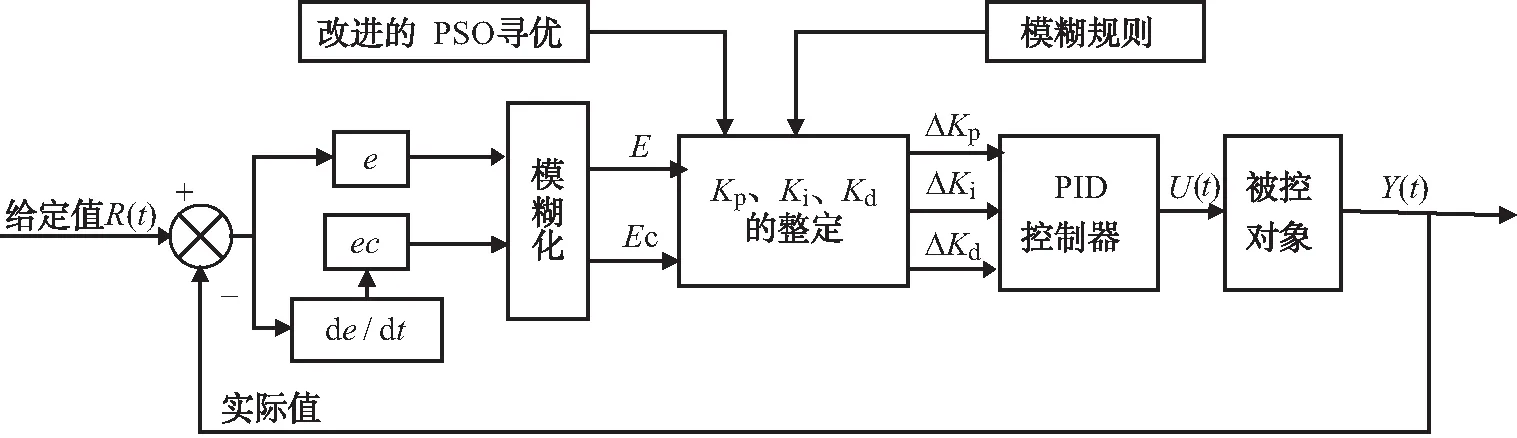
图5 经粒子群优化的模糊PID系统结构图

图6 鼓风机模糊PID控制系统

图6中，改进的PSO优化算法中寻优的解为Kp、Ki、Kd，在控制系统运行过程中寻找最优值.将模糊PID控制器、经过改进的PSO优化处理的模糊PID控制器及传统PID控制器三者进行仿真，并比较三者的输出曲线以获得如图7所示的对比曲线.

在图7，经改进的PSO算法优化的模糊PID控制与传统的PID控制、模糊PID控制相比较，都体现了比两者控制器较为优越的性能.与传统的PID输出曲线的3个指标相比较，都有显著的提高，分别是响应时间、超调量及稳定时间.经改进的PSO算法优化的模糊PID控制系统的响应时间最短，模糊PID的其次，PID控制的响应时间最长；在超调量方面，经改进的PSO算法优化的模糊PID控制系统的超调量几乎为零，模糊PID有较小的超调，而PID算法的超调量较大；在系统达到稳定时间方面，经PSO优化的模糊PID系统的稳定时间最短，即系统能在最短时间内运行在稳定状态，模糊PID的稳定时间中等，而相比较而言PID控制系统的稳定时间长，稳定性较差.综上所述，不管在响应时间、稳定时间还是在超调量上，经改进的PSO算法优化的模糊PID控制系统都体现出了较为优越的性能，能使鼓风机能在较短的时间内启动，较大程度消除了误差，达到稳定状态.这在提高汽车空调运行节约能耗方面也是非常有利的.

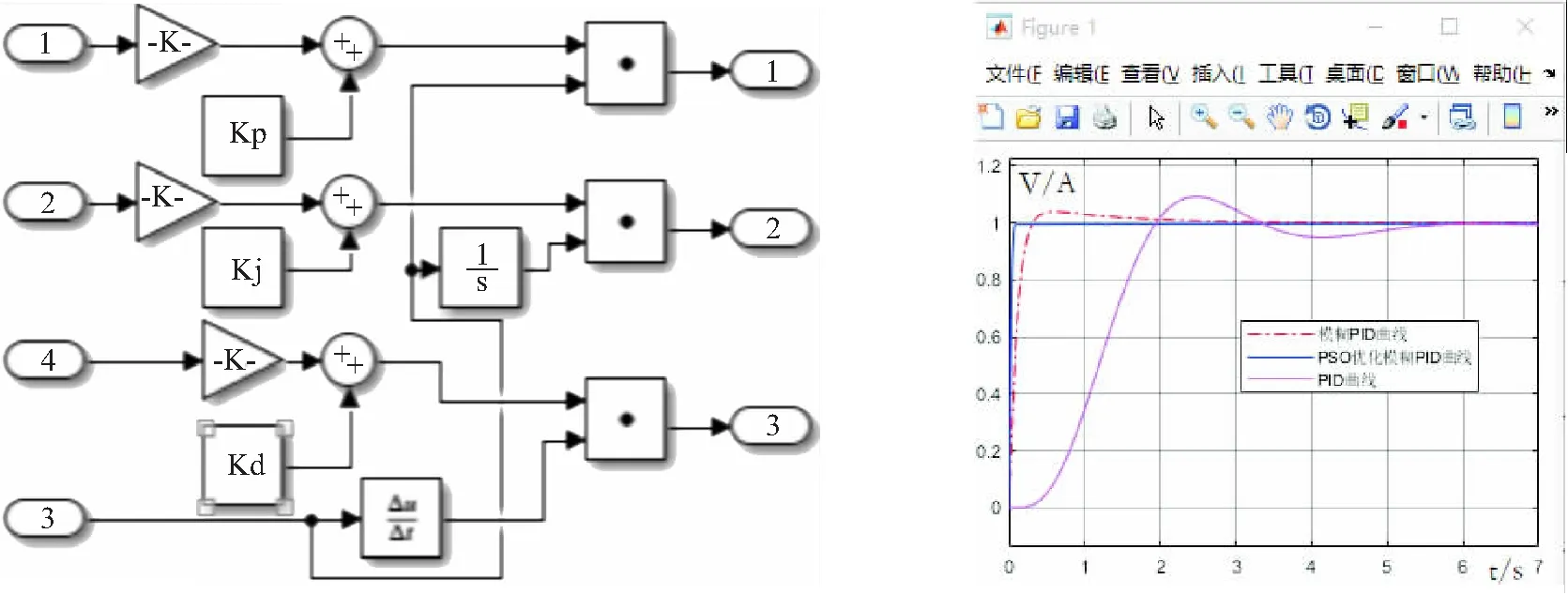
图7 经PSO优化的PID结构 图8 仿真结果曲线

4 结语

本文的研究对象在汽车空调控制器的应用中具有很强的通用性.在汽车空调鼓风机控制系统中，利用双输入、三输出的模糊器与PID理论相结合得到的模糊PID控制器，再根据实际需求对引进改进的粒子群优化算法对模糊PID控制器进行优化，是汽车空调控制器中有较大研究空间的控制策略，并且该控制策略能使汽车空调在运行过程中减少能耗的消耗.

在本文中对粒子群优化算法进行改进，对模糊控制器的输出进行最优值寻找，为汽车空调控制器提供了一定的技术思路和解决方案.目前该研究方案仅在Matlab平台上的仿真运行，并分析验证了此方案的可行性.但是具体的方案实施，仍需要在实践中验证.