基于箱线图异常检测的指数加权平滑预测模型
2021-01-27顾国庆李晓辉
顾国庆,李晓辉
(华北计算技术研究所,北京 100083)
0 引 言
无线传感网WSN(Wireless Sensor Network)是由大量边缘传感节点和少量汇聚节点组成的一种计算机网络,传感节点相互协作监控某一区域不同位置的环境状况并将采集到的实时数据上传至汇聚节点。这些传感节点广泛分布在一些监管困难甚至长期无人监管的恶劣环境中,通常采用自携式电池供电,因此如何减少传感节点能耗、延长传感节点寿命成为该行业的一大痛点[1-2]。
目前国内外学者主要从精简数据传输方面提出了一些解决方案,Lazaridis等人[3]在2003年提出了一种有界的传输数据压缩方案,同年又提出了一种使用恒定值作为预测值的预测方案;Lim等人[4]在2005年提出了2种不同的自适应线性预测模型;Santini等人[5]在2006年提出了最小均方差自适应预测模型;Wei等人[6]在2011年提出了一种结合卡尔曼滤波和灰色模型两者的预测方案;Razzaque等人[7]在2013年提出了3类数据预测方法,随机方式[8-10]、时间序列方式[11-12]和复杂算法方式[13];Raza等人[14]在2016年提出了包括wake-up receiver和专用感应设备的节能传感器网络模型;同年Tan等人[15]提出了基于前N项数据进行分层的LMS模型;余修武等人[16]在2017年提出了一种基于分簇的自适应的预测加权数据融合算法;魏煜等人[17]在2018年提出了基于线性预测模型和HeartBeat机制的LRPH算法来抵制丢包带来的影响,同时提出了LRSH算法来优化LRPH算法,减少冗余信息。
在实际监测环境中,传感节点有可能采集到异常数据,而大多数现有的精简数据传输方案会将异常数据视为正常数据,难以避免异常数据对模型预测带来的负面影响。因此,本文提出一种基于箱线图异常检测机制的指数平滑预测模型,该模型创新性地引入箱线图异常检测机制过滤异常点,同时为了更好地区分异常点和突发事件,引入短期环比作为判定依据,最终有效过滤掉异常数据,提高数据传输的精简程度和预测准确度,达到传感节点节能降耗的效果。
1 指数加权平滑预测模型
1.1 指数加权平滑预测模型概述
指数加权平滑预测模型[18]是一种特殊的加权移动平均方法,其对不同时间观察值赋予不等的指数权重,距离预测值越近的观察值被赋予的指数权重越大且呈指数变化。目前该模型在无线传感网数据预测方面具有易实现、准确度高以及低消耗等优势,Gaura等人[19]在2013年提出的L-SIP预测模型正是采用指数加权平滑滤波方式进行线性预测。
该模型存在3种具体表现形式:1)一次指数加权平滑针对没有趋势和季节性序列;2)双指数加权平滑针对存在趋势但没有季节性序列;3)三次指数加权平滑针对存在趋势且季节性序列。本文实验采用北京市密云区某监测点全天PM10值和北京市东四某监测点全天AQI值作为实验数据,PM10和AQI序列存在趋势但无季节性,因此采用双指数加权平滑法作为预测模型最为适宜。
1.2 双指数加权平滑预测模型原理
双指数加权平滑模型是从一次指数加权平滑模型演变而来,一次指数平滑计算公式为:
(1)

(2)
可以看出权重值根据距离由近到远呈指数递减规律,双指数加权平滑模型是在一次指数加权平滑模型基础上将趋势作为一个额外考量,保留了趋势的详细信息。双指数加权平滑计算公式为:
(3)

xt+T=AT+BTT
(4)
其中:
(5)
2 基于箱线图异常检测的双指数加权平滑预测模型
2.1 整体流程
本文提出的预测模型是在双指数加权平滑模型基础上,引入箱线图异常检测机制处理异常数据,同时通过短期环比判定突发事件,最终将结果汇聚到汇聚节点。该算法的数据处理流程如图1所示,其大致可以划分成4个阶段。

图1 数据处理流程
1)在数据采集初始化阶段,传感节点会以一定频率采集数据,如果传感节点正处于开机状态,那么会初始化传感节点和汇聚节点的预测模型;如果系统处于正常工作状态,则会跳过模型初始化的过程直接进入到下一个阶段。
2)在异常值检测阶段,传感节点采集到的检测值会与双指数加权平滑模型进行比较,如果差值在可接受范围内,则直接跳过数据突发事件判定阶段,传感节点不上传数据,汇聚节点采用预测值作为监测结果;如果预测值被判定为疑似异常点,则将疑似异常值按照队列的顺序存入滑动窗口,滑动窗口是在传感节点开辟的一块内存空间,用来存储连续疑似异常点。
3)在突发事件判定阶段,当滑动窗口存满数据时,取出滑动窗口所有值进行短期环比判断是否为集中或趋势数据集,如果是,则将该数据集全部上传至汇聚节点,修正模型参数;如果不是,则清空滑动窗口数据,传感节点不上传数据,同时汇聚节点采用预测值作为监测结果。
4)在数据汇聚阶段,汇聚节点同步传感节点信息,如果汇聚节点接收到传感节点上传的数据,则采用上传数据作为监测结果,否则采用模型预测值作为监测结果。
2.2 箱线图异常检测机制
2.2.1 确定箱线图参数
箱线图[19]是一种用作显示一组数据分散情况的统计图,用于反映数据分布特征。箱线图对异常数据的判定原理如下图2所示:

图2 箱线图异常数据判定
Q1为一组数据的第一四分位点,Xm为中位数,Q3为第三四分位点,IQR为Q3与Q1两数之差。当检测值小于Q1-1.5 IQR或大于Q3+1.5 IQR时,认为该值属于温和异常值;当检测值小于Q1-3 IQR或大于Q3+3 IQR时,认为该值属于极端异常值。异常值区边界的设定基于经验判断,大量实践表明该方法在处理异常数据方面性能表现优异。一方面,箱线图绘制仅依靠实际数据,不需要事先假定数据服从特定的分布形式,没有对数据做任何限制性要求,它真实直观反映数据变化趋势本来面貌;另一方面,箱线图判断异常值的标准以四分位数和四分位距为基础,四分位数具有一定耐抗性,多达25%的数据可以变得任意远而不会很大干扰四分位数,所以异常值不会对这个标准施加影响,识别结果更加客观。
2.2.2 异常检测过程
根据箱线图异常检测机制,当遇到陡然变化的数值时,异常检测系统将其判定为异常点,同时该数据被传感节点忽略不会上传至汇聚节点,以此类推,下一个监测数据乃至该突发事件产生的一批监测数据都会被忽略,无法上传到汇聚节点。此时就会产生新的问题:异常点和突发事件难以被区分开,从而突发事件可能会被系统视为连续异常点被过滤掉。对于任一突发事件,其必定会持续一段时间,在这段时间内必定会产生一批突发事件下的正常数据,如果能检测出这批数据本身具备趋势性或相对集中,就能判定出该批数据是某一事件产生的而非异常点。
本文通过引入滑动窗口暂存疑似突发事件的数据集,箱线图异常检测机制算法原理如下:

1:N←slide window size
2:X[N]←store exception data
3:while(true)
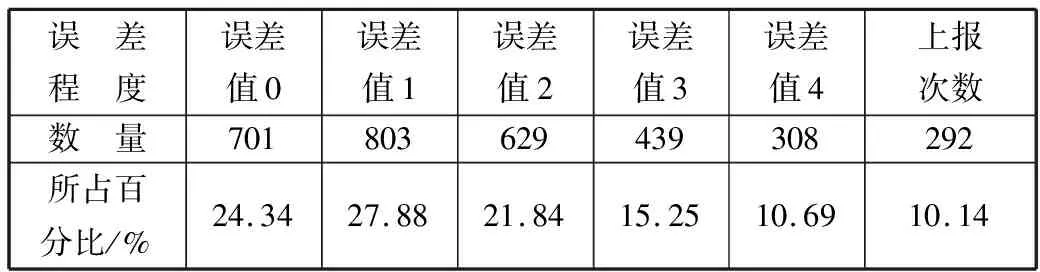
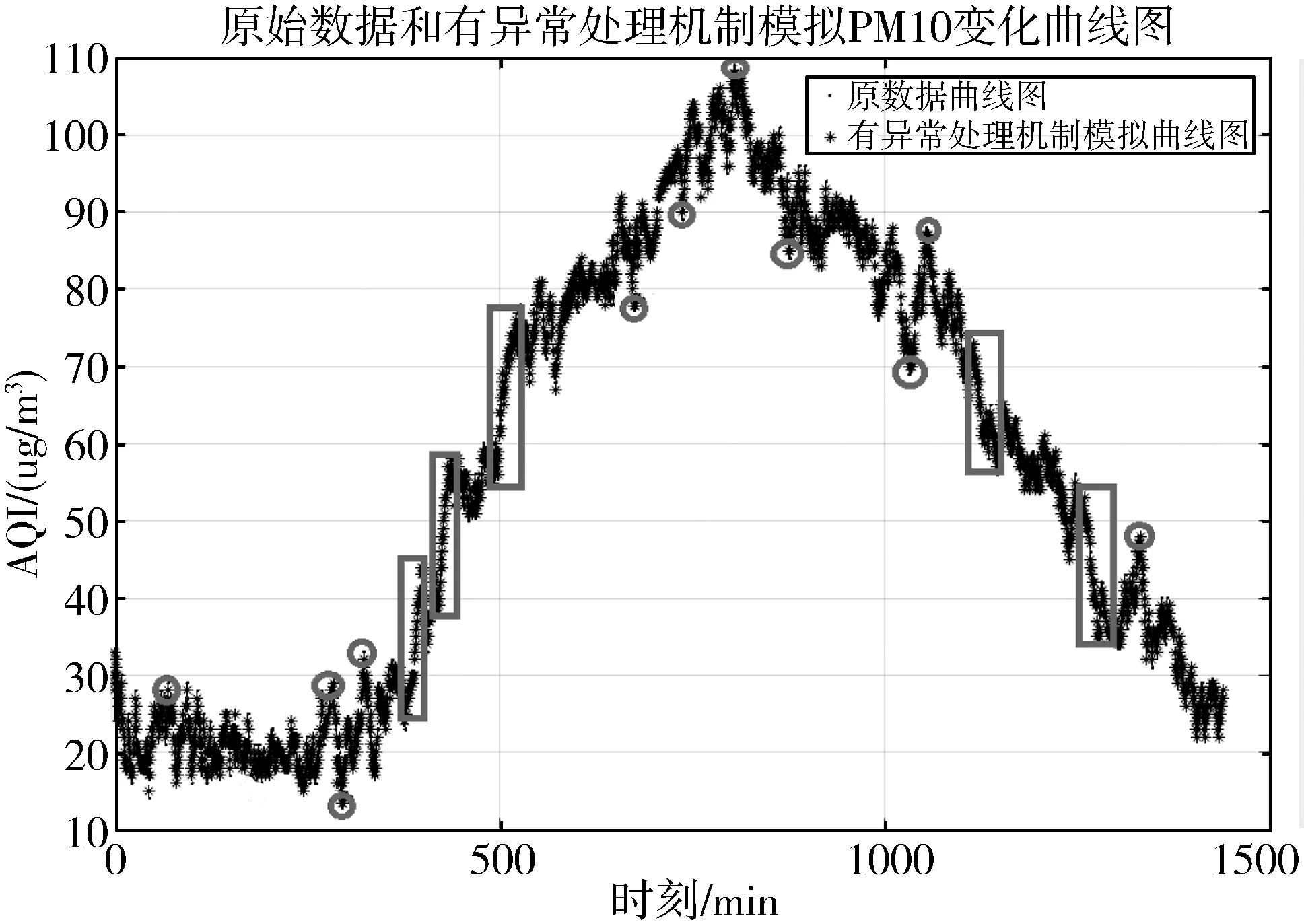
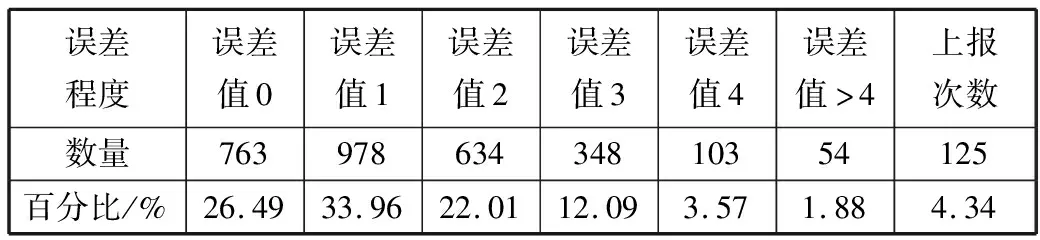
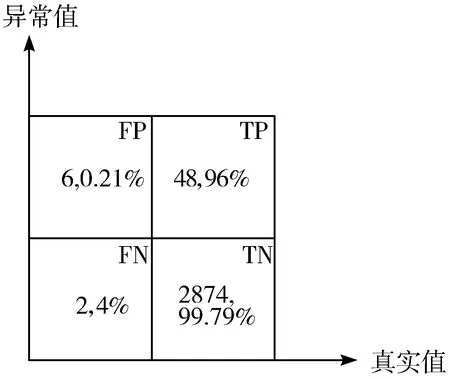
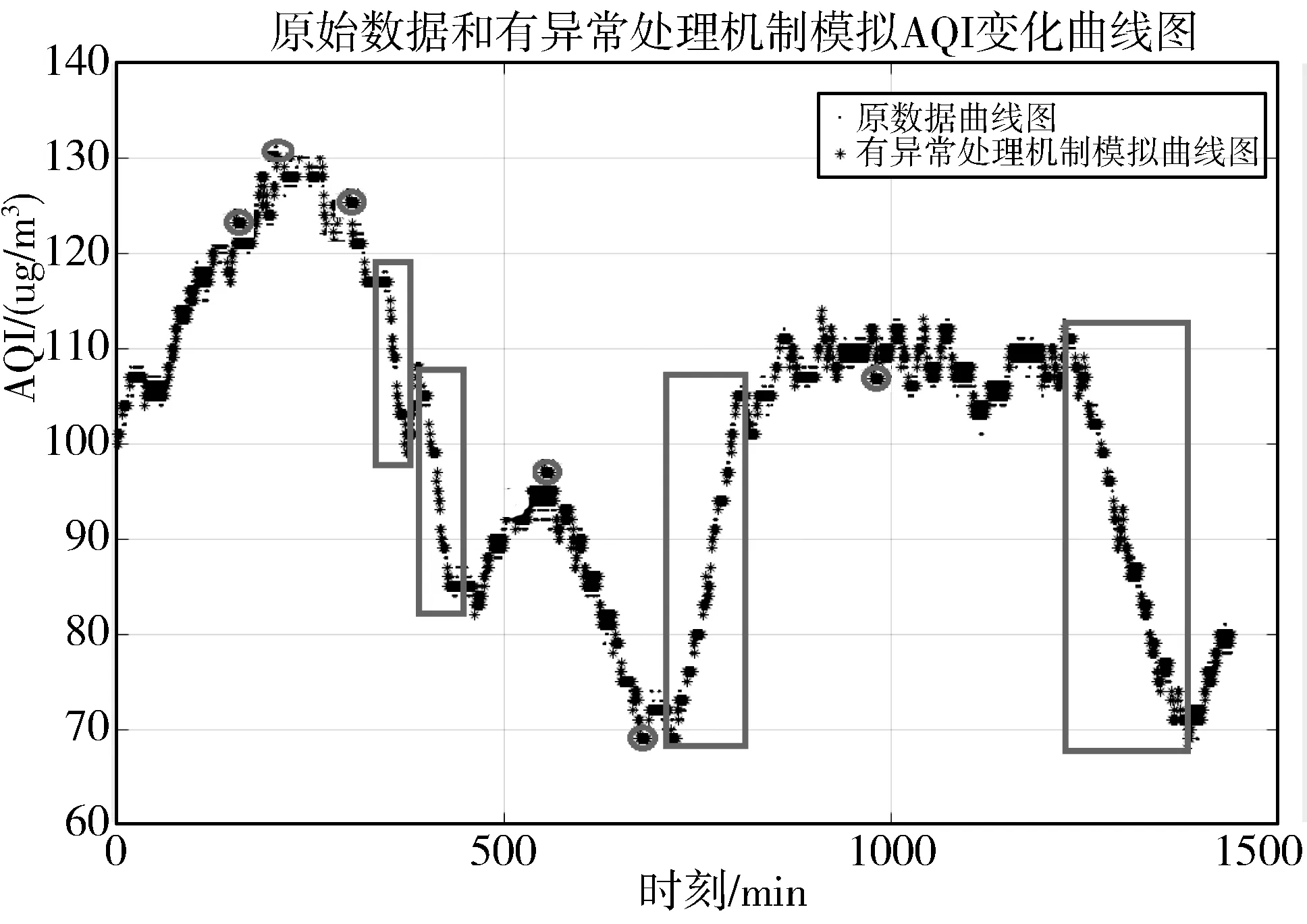
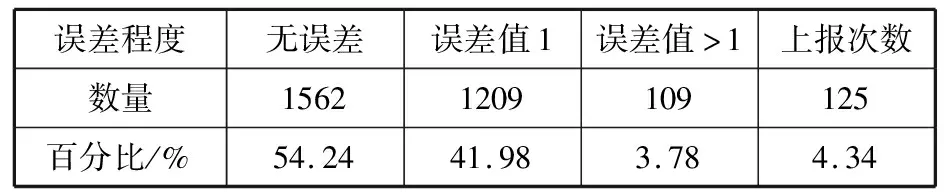
4:for(inti=0;i 5:if(exception data detected) 6:X[i]←exception data 7:i←i+1 8:if(iequalN) 9:break 10:if(no exception data detected) 11:cleanX 12:i←0 13:if(verifyXis an emergency) 14:reportXto sink node 15:modify model parameters 在传感节点开辟一块内存作为滑动窗口X用来存储疑似异常点,滑动窗口大小为N。当监测数据为疑似异常点时,将该数据按照队列顺序存入滑动窗口X中。如果滑动窗口X数据存满,则说明采集到的疑似异常数据量已经满足突发事件最小数据量,只需判断这批数据是否是突发事件,如果这批数据被判定为突发事件,则将这批数据上报至汇聚节点同时修改指数平滑加权模型;如果滑动窗口未存满时,检测到的数据不是疑似异常数据,则清空滑动窗口并将指针i重置为0。 2.3.1 确定短期环比参数 本文通过短期环比(SS)来判断一组数据是否具备趋势性或相对集中,如公式(6)所示: (6) 其中,threshold是动态阈值,根据实际监测环境设置,avg为这一组数的平均值,count_num是可接受超过动态阈值的数目,如果判定条件较宽松,count_num可设置为较大值;如果判定条件严格,count_num则需要设置为较小值,其设值范围在0~N之间。通过与动态阈值的比较,就可以判断出一组数据是否具备趋势性或相对集中。 2.3.2 突发事件判定过程 短期环比判定突发事件算法原理如下: 1:X[N]← short term chain data sets 2:threshold ← set manually according to the actual situation 3:count_num ← number of acceptable exceeding dynamic threshold 4:sum ← 0 , avg ← 0 5:temp_num ← number of exceeding dynamic threshold,default is 0 6:for(inti=0;i 7:sum+=X[i] 8:avg = sum/N 9:for(inti=0 ;i 10:if(|X[i]-avg|>threshold) 11:temp_num +=1 12:if(temp_num <= count_num) 13:this data set is normal 14:else 15:this data set is not normal 当滑动窗口存满数据触发了突发事件时,通过短期环比验证该数据集是否具备相对集中或具备趋势性的特征。具体流程如下: 1)取出滑动窗口的所有数据集,统计所有数据总和sum并计算出平均值avg; 2)依次遍历数据集的每个数据与平均值avg进行比较,若两者差值大于动态阈值threshold,超过动态阈值数目temp_num增加1; 3)遍历结束后,若temp_num小于等于count_num,则可以判定该数据集为突发事件而非异常数据。传感节点此时会将该数据集全部上传给汇聚节点,并同步更新预测模型参数。 本次实验使用Java语言实现,集成开发环境是IntelliJ IDEA,采用MATLAB绘制图形。硬件配置:Intel(R)Core(TM)i7-3770处理器、3.4 GHz最大主频、16 GB运行内存、1 TB磁盘大小、64位Win7操作系统。 本次实验数据集采用北京市密云区某监测点全天PM10监测值,为进一步验证模型的鲁棒性和普适性,又采用北京市东四某检测点全天AQI监测值不同地点和指标的数据作为对比实验数据集,仪器每隔30 s采集一次实验数据并记录,全天共产生2880个离散数据点。 为了便于研究异常数据对预测模型的影响,在原始数据集引入50个异常边缘尖锐点,首先不采用箱线图法异常检测机制,仅使用双指数加权平滑模型进行预测。经过多次粗细粒度划分,平滑指数设置为0.5为最佳,误差阈值设置为4,考虑到传感节点计算能力有限且距目标点太远的数据对目标点影响较小,所以本实验采用目标点前8位数据作为预测模型数据集。其预测情况如图3所示(其中圆圈圈出的尖锐点为部分引入异常点,矩形框出的变化剧烈数据集为部分突发事件),通过分析图3可以得出如下结论。 1)预测模型对边缘尖锐点或剧烈变化数据集拟合程度高,反而对变化不大的平稳数据集拟合出现少许波动。从本质上来说,前者并非拟合而来,反而是拟合偏差超过误差范围,传感节点直接上报数据,汇聚节点直接采用上报数据,从而出现了边缘尖锐点拟合度高,平稳数据集拟合度低的反常现象。 2)通过结论1分析可知,传感节点上报往往发生在监测结果为边缘尖锐点或剧烈变化数据集上,且通常会出现拖尾现象,即边缘尖锐点随后的一段数据也会出现上报,这是因为边缘尖锐点作为预测模型参数直接影响了模型对随后数据的预测。将预测情况进一步绘制成表1。 表1 各误差程度具体分布情况(无异常检测) 采用本文提出的基于箱线图异常检测的二次指数加权平滑算法进行预测,结果如图4所示。 图4 引入异常检测机制模型预测结果 将预测情况进一步绘制成表2。 表2 各误差程度具体分布情况(异常检测) 相比于普通无异常处理机制的预测模型,有异常处理机制的预测模型无误差预测率提高了2.15个百分点,误差值为1预测率提高了6.08个百分点,误差值为2预测率提高了0.17个百分点,误差值为3预测率降低了3.16个百分点,误差值为4预测率降低了7.12个百分点,上报率降低了5.8个百分点。通过图4标出的部分圆圈可知,原始数据集大多数边缘尖锐异常点通过异常检测机制或判定为异常点,或经过平滑处理,同时通过短期环比判定机制较好区分开边缘尖锐异常点和突发事件,从而预测并上报了突发事件完整数据。对异常点的具体预测情况如图5所示。 图5 异常点预测结果 该模型成功过滤掉48个异常点,有效率高达96%,同时仅将6个正常点误判成异常点,阳性误判率仅为0.21%,从整体数据可以看出,引入异常检测机制有效消减了异常点带来的负面影响,从而显著提高了数据精简传输率和预测精准度。 为了进一步验证基于箱线图法异常检测机制的双指数加权平滑预测模型对异常点和突发事件的处理效果,本文进行不同数据集下的对照实验,对照实验数据为北京市东四某采集点全天AQI的监测值,传感节点每隔30 s采集一次数据,全天共有2880个离散点。为了进一步研究异常数据对预测模型的影响,在原始数据集引入100个边缘尖锐异常点,未采用异常检测机制的预测情况如图6所示。 图6 无异常检测机制预测模型结果(对照组) 将预测情况进一步绘制成表3。 表3 对照组各误差程度具体分布情况(无异常检测) 由于没有排除异常的检测机制,当检测到异常数据时,预测模型会将该异常数据视为正常数据,同时将该异常数据对比预测值,发现两者差值远远超出了误差阈值,此情况不符合精简传输策略,所以传感节点会将此异常数据连同预测模型所需的前面N-1个数据一起上传同步汇聚节点模型参数。由于异常数据并不会持久存在,在出现个别次数后又会回落到正常的检测范围,此时预测模型由于受到异常数据影响反而会使正常数据与预测值超出误差阈值,此时又会出现上传情况。 该实验监测到的AQI数据较集中,连续数据差值一般不超过1,所以动态阈值设置为1,经过2轮粗细粒度划分,平滑系数为0.4时表现最佳。其平稳阶段的数据浮动范围在2以内,此时模型更倾向于预测成一直线。采用本文提出的基于箱线图异常检测的双指数加权平滑算法进行预测,结果如图7所示。 图7 引入异常检测机制预测模型结果(对照组) 将预测情况进一步绘制成表4。 表4 对照组各误差程度具体分布情况(异常检测) 相比于普通无异常处理机制的预测模型,有异常处理机制的预测模型无误差预测率提高了2.02个百分点,误差值为1预测率降低了5.8%个百分点。对异常点的具体预测情况如图8所示。 图8 异常点预测结果(对照组) 该模型成功过滤掉98个异常点,有效率高达98%,同时仅将11个正常点误判成异常点,阳性误判率仅为0.38%,通过对照实验组进一步验证了引入异常检测机制在不同数据集、平滑系数变动和不同动态阈值多种条件下都能有效消减异常点带来的负面影响,从而显著提高数据精简传输率和预测精准度,取得良好的效果。 本文针对无线传感网在精简传输过程中如何过滤异常点和判定突发事件等问题进行研究,有效地提高了预测模型准确度,进一步减少了边缘传感节点上报次数,提升了数据传输精简程度。本文首先分析了异常数据点对预测模型的影响,依据实际应用场景提出了基于箱线图异常检测的指数加权平滑算法的预测模型,同时通过短期环比区分异常点和突发事件。实验结果表明,该预测模型可以有效过滤引入的异常点,同时较准确地区分开异常点和突发事件,明显提高了模型预测准确性和数据传输精简程度。下一步工作将箱线图异常检测机制更广泛地应用到其他预测模型,同时采用各种应用场景的监测数据作为测试数据集,不断修正调整异常检测机制,使其更具鲁棒性和应用广泛性。
2.3 短期环比判定突发事件


3 实验验证
3.1 实验环境
3.2 实验数据
3.3 实验结论及对比分析



4 结束语
