机器人导航路径的多种群博弈蚁群规划策略

陈银燕 ，高安邦

（1.江苏电子产品装备制造工程技术研究开发中心，江苏 淮安 223003；2.淮安信息职业技术学院，江苏 淮安 223003；3.哈尔滨理工大学，黑龙江 哈尔滨 150080）

1 引言

移动机器人在国民生产生活中应用领域越来越广，发挥作用也越来越大，移动机器人的行走路径直接决定了其工作效率和自身安全，是进行其他生产活动或服务活动的基础[1]。因此，研究机器人导航路径规划问题具有明显的经济意义和安全意义。

机器人路径规划的核心要求是在满足约束条件下，规划一条从起始点到目标点的无碰路径，且此路径满足某种评价标准下的最优。根据对环境的掌握程度和环境中障碍物动态特性，一般将路径规划分为全局规划和局部规划[2]。对于静态的、全局已知的环境，使用全局规划方法；对于动态的、未知的环境使用局部规划方法。从规划方法的提出时间划分，可以分为传统规划方法和智能仿生规划方法。传统规划方法包括Dijkstra 算法[3]、人工势场法[4]、模糊逻辑法、栅格法[5]等。智能仿生规划方法包括遗传算法[6]、神经网络[7]、蚁群算法和粒子群算法[8]等，此类方法的特点是模拟生物的某种生理现象或发挥群体智慧对工作路径寻优。由于智能仿生算法的整体寻优水平较好，因此规划的路径质量相对较高，因此成了当前路径规划研究的热点。当前机器人工作场景多种多样，使得单一固定的机器人路径规划方法难以满足要求。总的来讲，机器人路径规划研究趋势为：（1）全局规划与局部规划相结合；（2）传统规划方法与智能规划方法融合发展；（3）新型智能规划算法不断提出。

研究了静态栅格环境下导航路径规划问题，提出了多种群博弈蚁群算法的规划方法。将博弈论应用于多种群协同与配合中，有效增加了算法在整个迭代过程中的路径多样性，达到了降低工作路径长度、减少迭代次数、增加路径平滑性的目的。

2 机器人工作环境模型

2.1 栅格模型

常用的环境建模方法包括可视图法、极坐标法、Voronoi 图法、单元树法和栅格法等，其中栅格法具有原理简单、易于存储、栅格大小可调等诸多优点，因此选择建立工作环境的栅格模型。

栅格法是使用固定大小的栅格将工作区域进行分割，栅格内含有障碍物的栅格称为障碍物栅格，不含有障碍物的栅格称为非障碍物栅格。若障碍物没有占满一个栅格，则使用膨胀法使其占满栅格，而后根据栅格内含有障碍物情况进行属性赋值。一般将非障碍物栅格赋值为0，将障碍物栅格赋值为1。至此栅格建模法将虚拟的二维工作环境转化为二维矩阵，非常易于建立和存储。

图1 某环境栅格模型Fig.1 Grid Model of Some Environment

某工作环境的栅格模型，如图1 所示。对应的二维矩阵模型为。

2.2 栅格编码

栅格编码方法有两种，分别为顺序编码法和直角坐标法。顺序编码法是从上至下，由左到右依次编码；直角坐标法是第i 行第j 列的栅格坐标记为（xi，yj）。则顺序编码为k 的栅格与直角坐标法（xi，yj）转换关系为：

式中：Nh—每一行的栅格数；mod—取余函数；int—舍余取整函数。

另外在此说明的是，栅格法包括四叉树法和八叉树法。四叉树法是指机器人可选栅格限定在当前栅格的上下左右等4 个栅格，八叉树法是指机器人可选栅格为当前栅格的上、下、左、右、左上、左下、右上、右下等8 个栅格。使用的是八叉树栅格法。

3 算法改进相关知识

为了在栅格环境下规划出机器人最优路径，提出了多种群博弈蚁群算法，设计了一个主种群和若干个从种群，使用博弈论实现主从种群间合作和从种群间协调，同时使用信息熵作为不同博弈策略的激发条件。为了下节更加清晰的构造多种群博弈算法，本节首先介绍算法改进的相关知识。

3.1 蚁群系统与最大最小蚂蚁系统

常用的蚁群算法有蚁群系统和最大最小蚂蚁系统两种，两种蚁群算法的最大区别体现在信息素更新方面。

蚁群系统的信息素更新包括局部更新和全局更新两个方面。局部更新方法为蚂蚁从节点i 运动至节点j 后，则在路径ij 上进行信息素更新，方法为：

式中：λ—局部信息素挥发系数；τ0—信息素初值。

蚁群系统的全局信息素更新在完成一次迭代后，只针对全局最优路径进行，方法为：

式中：ρ—全局信息素挥发系数；Vτij—信息素增量；Lgb—一次迭代后全局最优路径长度。

最大最小蚂蚁系统的信息素更新强调两个方面：一是只进行全局信息素更新，即在完成一次迭代后，对本次迭代最优路径进行信息素更新，信息素更新公式同式（3）一致；二是为了平衡收敛性和多样性，对路径信息素浓度设置上下限。

3.2 博弈论

博弈论也称为对策论，是研究具有对抗或竞争行为的理论[9]。在博弈论中，参加斗争或竞争的各方具有各自的利益或目标，各方需充分考虑其他个体所有的可能行动方案，选择对自身最有利的行动方案。下面介绍博弈论中重要的三个概念：Nash 均衡、帕累托最优和夏普里值。

3.2.1 Nash 均衡

Nash 均衡是指所有参与者这样的组合策略，在此组合策略下，任何参与者单方面改变策略都得不到好处。Nash 均衡是一种非合作博弈状态。

数学定义为，对于博弈G=｛N，Ai，ui｝，式中N 为博弈参与者数量，Ai=｛aij｝为博弈参与者i 行动策略集合，ui为参与者i 基于行动 Ai的收益。如果在某个策略组合中，任一参与者的行动策略a*i都是其余参与者行动策略组合的最佳对策，也即ui对于任意aij∈Ai都成立，则称为博弈 G 的一个 Nash 平衡。

3.2.2 帕累托最优

帕累托最优是一种理想的资源分配状态。对于博弈G=｛N，Ai，ui｝，从一种策略组合改变为另一种策略组合时′时，在没有任何参与者收益ui减小的前提下，至少使一个参与者收益变大，此过程为帕累托改进。帕累托最优是指不存在帕累托改进的余地，即资源分配达到了最理想的收益状态。达到帕累托最优的渠道是帕累托改进。

3.2.3 夏普里值

夏普里值是一种分配方式，分配原则是所得与自己贡献相等。博弈参与者i 的利益分配函数或期望贡献为：

式中：N—所有参与者组成的大联盟；S—任意参与者组成的小联盟；n—大联盟参与者数量；k—小联盟S 参与者数量：v（S）-v（S-｛i｝）—参与者 i 对联盟 S 的决策影响度。

3.3 信息熵

信息熵可用于描述随机事件发生的不确定性，或者可用于描述随机变量的随机性。对于某一随机变量X，其信息熵定义[10]为：

式中：H（X）—信息熵；x—随机变量 X 的取值；p（x）—事件的发生概率。

在随机事件或随机变量中，每个可能事件发生的概率越均衡，则随机事件或随机变量的信息熵越大。因此在后文中，使用信息熵描述算法路径多样性，信息熵越大说明路径多样性越好。

4 多种群博弈蚁群算法

4.1 多种群博弈算法框架

算法多样性决定了算法对工作区域的搜索广度，同时也决定了最优路径的搜索概率，因此提高算法多样性可以极大程度提高算法的搜索性能。鉴于这一思想，提出了多种群博弈蚁群算法，旨在平衡算法的多样性和收敛性。

设计的多种群博弈蚁群算法原理框架，如图2 所示。

图2 多种群博弈蚁群算法原理Fig.2 Principle of Multi-population Game Ant Colony Algorithm

由1 个主种群和2 个从种群组成，为了实现种群之间的信息交流与协作配合，提出了4 种机制，分别为合作博弈机制、奖惩机制、协调博弈机制、针锋相对机制。主种群与从种群之间使用合作博弈机制进行交流与配合，使主种群自适应进化；奖惩机制是主种群对从种群的单方向作用机制，可以强调优化从种群的作用，对较差从种群对主种群的影响减小。从种群的信息交流与合作机制为协调博弈机制和针锋相对机制，这两种机制为并行机制，协调博弈机制是为了提高所有从种群的路径质量，达到帕累托最优状态；针锋相对机制为了提高较差种群的影响力，将较差种群的信息素重新分布。两种并行机制相互配合从而提高整个从种群群体的路径质量和多样性。

不同机制之间的切换条件以本次迭代路径的信息熵为依据，在介绍不同机制时会一一给出。

4.2 合作博弈机制

合作博弈机制是主种群与从种群之间的博弈机制，是从种群根据自身搜索结果向主种群反馈的最佳信息，也可以理解为从种群将自身的搜索经验汇报给主种群，从而提高主种群搜索效率和收敛性。

由经验可知，同一路径规划问题，多数次优解或类似最优解都有相同的路径片段，而此路径片段也是最优解的必经路段。基于这一经验，从从种群规划的多数类似最优解中提取出重复路段，然后传递给主种群，从而减少主种群路径规划的任务量，实现了从种群对路径的预处理或预挑选。

合作博弈机制需要一个触发条件，使用信息加权熵进行构造，信息加权熵体现了从种群对主种群的影响力，当影响力足够大时才能够触发合作博弈机制。因此设定一个阈值，当信息加权熵大于此阈值时实施合作博弈机制。信息加权熵计算方法为：

式中：HW—信息加权熵；Hk—从种群k 的信息熵；wk—从种群k 的权值，使用夏普里值法确定，即权值与贡献相等。

4.3 奖惩机制

奖惩机制是主种群对从种群的单方向作用机制，对表现优的从种群进行奖励，对表现差的从种群进行惩罚，这一机制类似于博弈论中的拍卖模型。主种群对从种群的奖惩作用于算法的信息素上，信息素奖惩方式为：

式中：Vτi—从种群i 产生的信息素增量，当从种群i 被奖励时则信息素增量增加1.2 倍，被惩罚时则减小1.2 倍。

通过式（7）给出的信息素奖惩机制，表现好的从种群就能够留下更强浓度的信息素供主种群参考，使主种群向表现好的从种群学习，吸取较优从种群的搜索经验，有利于提高算法搜索速度和精度。奖惩机制贯穿在整个算法执行过程中，无需触发条件。

4.4 针锋相对机制

针锋相对是一种博弈策略，它是指当有从种群对当前状态不满时，要求重新进行利益分配的策略，也即由一个Nash 平衡转化为另一个Nash 平衡。使用针锋相对机制是为了防止路径较为单一的从种群出现，从而提高从种群的路径多样性。

针锋相对机制触发条件为至少一个从种群的信息熵较小，超过了设定阈值。

当满足触发条件时，对较差的从种群信息素执行融合操作，为：

式中：n—从种群数量；Pk—从种群k 当前的信息素矩阵；wk—从种群k 对较差从种群的影响系数，取值为（0，1），另外将自身种群对自身影响力设定为0，即自身的信息素矩阵不参与计算。

4.5 协调博弈机制

协调博弈机制是跟随者之间的博弈机制，旨在提高所有从种群的路径质量，操作方法为在没有任何从种群性能变差的前提下，至少使一个从种群的性能提高，也即通过不断帕累托改进，提高从种群整体性能。从种群性能的评判标准使用信息熵、路径质量和迭代次数构造，为：

式中：Vi—算法性能指标；Si—当前信息熵与历史最大信息熵比值；Ai—当前最优解与理论最优解的反比；Ci—当前迭代最小收敛次数与本子群收敛次数的比值。通过式（9）可以看出，Vi取值为（0，1）之间，其值越大则说明算法性能越好。

针锋相对机制触发条件为两个从种群的信息熵之差超过设定阈值。阈值根据当前从种群整体协同状态自适应调整，方法为：

式中：T—触发阈值；VT—增量。式（10）表示，当经过帕累托改进得到优化时，则阈值保持不变；当经过帕累托改进没有得到优化时，说明整体协同状态已经处于较高水平，难以再进行提高，此时提高阈值减少协调博弈触发次数。

4.6 多种群博弈蚁群算法流程

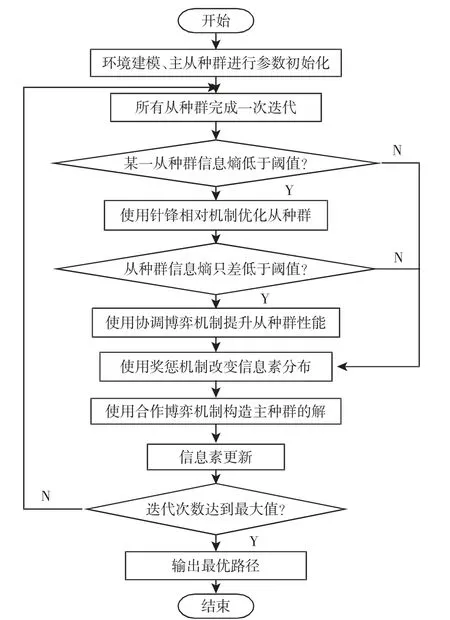
图3 多种群博弈蚁群算法流程Fig.3 Flow of Multi-population Game Ant Colony Algorithm

在多种群博弈蚁群算法中，主蚁群使用蚁群系统，2 个从种群分别使用蚁群系统和最大最小蚂蚁系统。将合作博弈机制、奖惩机制、针锋相对机制和协调博弈机制融入到多种群博弈算法中，得到算法流程，如图3 所示。

5 仿真验证与分析

5.1 算法多样性验证

使用博弈论实现多种群蚁群算法间的信息交流与合作，通过增加路径多样性提高路径遍历性和最优路径被搜索概率，因此本节对算法多样性进行验证。

蚁群算法参数设置为：最大迭代次数为2000，蚂蚁数量为20，局部信息素挥发因子为0.1，全局信息素挥发因子为0.1，启发式因子为2，信息素因子为1，信息素强度为1。

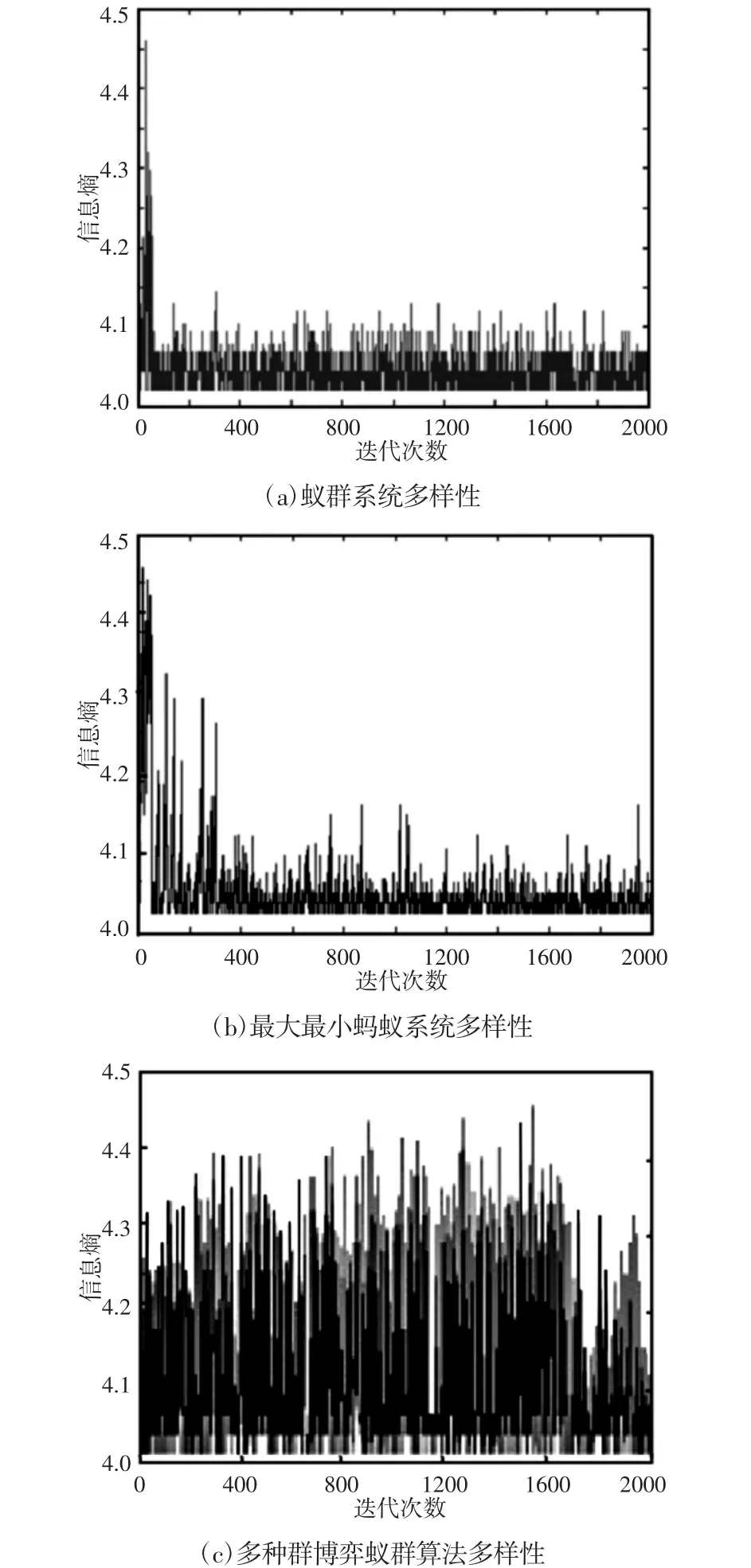
图4 不同算法迭代过程中路径多样性Fig.4 Path Diversity in Iteration Process of Different Algorithm

以TSP 测试库中中等规模的测试函数pr107 为算例进行验证，为了形成对比效果，分别使用蚁群系统（Ant Colony System，ACS）、最大最小蚂蚁系统（Max Min Ant System，MMAS）、多种群博弈蚁群算法（Multi-population Game Ant Colony Algorithm，MP－GAC）进行路径规划，每个算法各自独立运行10 次，选择规划的最优路径统计结果进行展示，三种算法在迭代过程中路径多样性，如图4 所示。

从图中可以看出，蚁群系统和最大最小蚂蚁系统在迭代初期由于信息素分别较为均匀，因此路径多样性较好；但是随着算法的迭代和信息素集中分布于若干路径，路径多样性急剧下降。多种群博弈蚁群算法的路径多样性在整个迭代过程中均保持较高水平，提高了路径遍历性和最优路径被搜索概率。

5.2 路径规划仿真分析

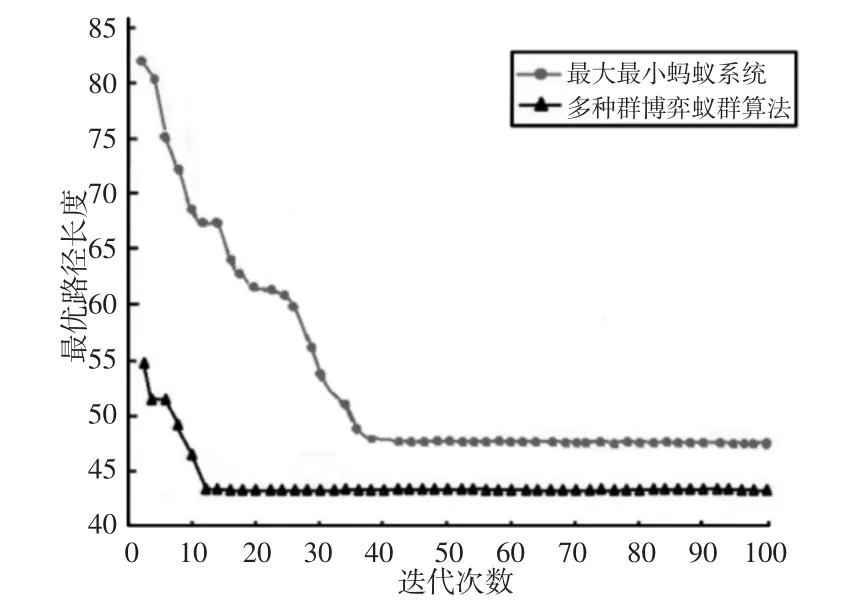
图5 路径长度迭代曲线Fig.5 Path Length Iteration Curve

图6 两种算法规划的最优路径Fig.6 Optimal Path Planned by the Two Algorithms

为了验证多种群博弈蚁群算法在栅格环境下的路径规划性能，同时使用最大最小蚂蚁系统、多种群博弈蚁群算法在栅格环境下进行路径规划，算法最大迭代次数设置为100，其余参数设置与5.1 节不变，迭代过程中最优路径长度随迭代次数变化曲线，如图5 所示。两种算法规划的最优路径，如图6 所示。

从图5 中可以看出，多种群博弈蚁群算法规划的路径长度随迭代次数下降极快，且在迭代12 次时搜索到最优路径。而最大最小蚂蚁系统规划路径长度下降速度相对较慢，在迭代至44 次时路径长度不再下降。从最优路径长度来看，多种群博弈蚁群算法规划的路径长度明显小于最大最小蚂蚁系统。

从图6 可以看出，多种群博弈蚁群算法规划的最优路径长度和平滑度明显优于最大最小蚂蚁系统。经计算，最大最小蚂蚁系统规划的最优路径长度为46.113，搜索到最优路径时迭代次数为44 次，路径拐点数量为19 个；多种群博弈蚁群算法规划的最优路径长度为43.355，比最大最小蚁群算法减少了5.98%；搜索到最优路径时迭代次数为12 次，远远小于最大最小蚂蚁算法；路径拐点数量为10 个，是最大最小蚂蚁算法规划路径的约一半，说明算法规划路径平滑度远远优于最大最小蚂蚁算法。综上所述，多种群博弈蚁群算法的最优路径长度、迭代次数、路径平滑度均优于最大最小蚂蚁算法，这是因为从种群之间的协调博弈机制和针锋相对机制有效协调了从种群之间的配合和共同进步，主从种群之间的合作博弈机制使从种群将自身搜索经验和路径片段传递给主种群，极大地提高了主种群路径质量和搜索效率，使多种群博弈蚁群算法的路径规划结果更优。

6 结论

研究了栅格环境下机器人路径导航算法，提出了多种群博弈蚁群算法的路径规划方法。经过研究，得出以下结论：（1）协调博弈机制和针锋相对机制可以提高从种群整体的路径多样性和路径质量；（2）合作博弈机制能够有效将从种群搜索经验和较优片段传递给主种群，降低主种群搜索工作量，提高搜索效率；（3）多种群博弈可以有效提高蚁群算法的多样性，从而提高搜索性能和路径规划质量。