曲率可控双轮自平衡机器人路径规划
2021-01-27牛雪娟陈国振孙宏图
牛雪娟,陈国振,孙宏图
(天津工业大学机械工程学院,天津 300387)
1 引言
双轮自平衡机器人属于轮式移动机器人中的一种,其路径规划是一个复杂的问题。常用的路径规划算法只关注了路径的有无碰撞,而对路径的可行性没有给予过多的关注。这是因为路劲规划对轮式移动机器人的运动学或其他几何约束不予考虑。
双轮自平衡机器人的特点是零半径回转、占地面积小和重心高[1]。正是由于其重心高的特点,在高曲率轨迹曲线快速转向时有侧向倾覆的危险。因此期望双轮自平衡机器人的运动轨迹是一条低曲率轨迹曲线。常用的平滑轨迹曲线有回旋曲线,贝赛尔曲线,立方螺旋线和B 样条曲线[2-5]。文献[3]运用分段贝塞尔曲线克服了高连续性需要高阶数曲线的问题,使得轨迹曲线具有低阶数、高连续性的特点,但是由于贝赛尔曲线的固有特性使得轨迹曲线灵活性差,不利于调节曲线曲率。文献[4]运用立方螺旋线作为过渡曲线连接直线与弧线,保证轨迹的曲率连续性,但其弧线曲率为定值,在转向时需要进行速度规划。文献[5]提出了一种速度曲率函数,使得机器人以变速度转向,减小了离心力对其平稳性的影响,但是其主要使用于车轮在三个及以上的机器人。对于双轮自平衡机器人而言,其在加减速的运动过程中为了保持车身的运动平衡会出现前后摆动的现象。
因此,采用三次B 样条曲线作为轨迹曲线,在保证轨迹曲线曲率连续性[6]的基础上,根据其基函数的局部支撑性,提出一种控制点的移动方法,使得其满足最大曲率约束条件,减小因转向速度快和重心高引起的车身倾斜,使得双轮自平衡机器人在无倾斜状态下以较快速度匀速平稳运动。
2 双轮自平衡机器人模型建立及分析
2.1 双轮自平衡机器人运动学建模
由于双轮自平衡机器人是基于两轮的速度差来完成曲线运动,故参照差速驱动移动机器人建立运动学模型[7],如图1 所示。
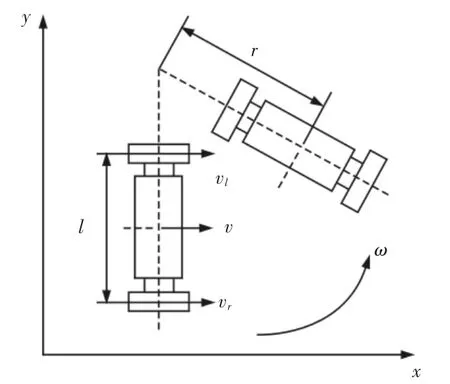
图1 运动学模型Fig.1 Kinematic Model
定义左轮的线速度为vl,右轮的线速度为vr,两轮间的距离为l。前进速度v 和转向角速度ω 可以用vl和vr来描述:

显然,依式(1)可以计算出曲率k,曲率k 描述如下:

从式(2)可以注意到,如果两车轮以相反的方向转动,随着两车轮线速度在数值上的接近,轨迹曲率值将会一直增大。然而,若期望双轮自平衡机器人以高线速度运动,那么在实际运动中应该避免两车轮以异号的线速度来实现急转弯,因为短时间内的大范围调速容易造成电机的过载。如果两车轮线速度均为正值并以某一给定的线速度 v 为上界(即 vl,vr∈[0,v]),则依据公式(2)计算得出的曲率 k 有界,其取值区间为[-2/l,2/l]。
2.2 曲率对双轮自平衡机器人侧向稳定性影响
双轮自平衡机器人在前进与后退方向上具有动态稳定性,但是在侧向上是静态稳定的。由于这个原因,其在高速运动时转向受到限制,因为离心力会导致车身不稳定和倾斜,受力分析,如图2 所示。

图2 双轮自平衡机器人受力分析Fig.2 Force Analysis of Two-Wheel Self-Balancing Robot
离心力可以通过下述公式描述:
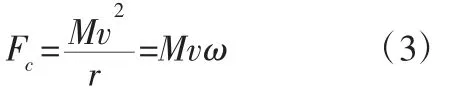
式中:Fc—离心力;M—双轮平衡车整体重量;v—前进速度;ω—旋转角速度;r—旋转半径。
在转向时,小的离心力对双轮自平衡机器人的侧向稳定性不会产生较大的影响,但当其增大到某一值时,其会处于倾斜的一种临界稳定状态。当离心力产生的力矩大于重力产生的力矩时,这种稳定状态将被破坏,使双轮平衡车发生倾斜。
从图2 可以得出发生倾斜时离心力临界值的计算公式:

式中:g—重力加速度;l—两轮间距离;h—重心的高。
将式(2)和式(3)带入式(4)中可得出不同前进速度下的临界曲率,如下:

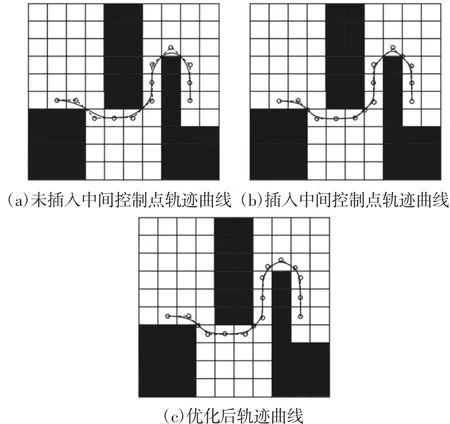
综合2.1 和2.2 节所述,假设双轮平衡车仅在一个方向上运动(如0 通常情况下,双轮自平衡机器人可以通过限制前进速度和旋转角速度或增加车轮的宽度来避免这种形式的倾斜。但是这两种解决方案都不理想,因为第一种解决方案限制了运动速度,第二种解决方案增加了机器人的占地面积。故我们希望通过利用轨迹曲线的灵活性降低曲率值,来保证双轮平衡车的运动速度和其体积小巧的特点。 三次B 样条曲线可以表示为: 对于三次B 样条曲线的一、二阶导数可用如下公式计算: 图3 轨迹曲线对比Fig.3 Trajectory Curve Comparison 图4 轨迹曲线碰撞Fig.4 Trajectory Curve Collision 根据双轮自平衡机器人的大小,对地图上的障碍物进行扩展,将地图进行栅格化处理。使用A*算法[8]搜索最短路径,并将搜索到的路径点作为控制点,生成三次B 样条曲线来平滑运动轨迹。相比较于轨迹曲线经过路径点的方法,该方法可以得到更逼近于搜索的路径且距离更短,如图3(a)、图3(b)所示。其中,红色线为A*算法搜索出的线段路径,蓝色线为平滑的轨迹曲线。但是以路径点为控制点生成的三次B 样条轨迹曲线在转向处会与障碍物发生碰撞,如图4(a)、图4(b)所示。为此,我们通过在转向处两个连续控制点的中点处插入一个新的控制点,来迫使三次B 样条曲线[9]逼近控制多边形,从而达到避障的目的。而由A*算法搜索处的路径,在转向处多为斜对角线,则添加的中间控制点就会落于障碍物的直角点上,轨迹曲线仍会发生碰撞,故我们提出一种碰撞检测方法和解决办法。 使用了高效样条碰撞检测算法[10]的思想。三次B 样条轨迹曲线为 C(x(u),y(u)),障碍物表示为 B,对于∀u∈[0,1]无碰撞条件为 C(x(u),y(u))∩B=φ。若检测到轨迹有碰撞,则对于∀u∈[0,1],有 C(x(u),y(u))∩B≠φ。令 d(C(u),B)为 C(u)和 B 之间的距离。t 是双轮自平衡机器人车身的边界条件。如果检测到碰撞,则ρ≤1。碰撞检测公式如下: 在式(8)中,双轮自平衡机器人的车身边界t 应小于C(u)和B 之间的距离。为使轨迹曲线无碰撞,将转向分为两种:分别为同号曲率转向,异号曲率连续转向,如图4(c)、图4(d)所示。对于同号曲率转向,将转向处的中间控制点沿45°线远离障碍物直角点的方向移动3/2t 的距离,而共线的相邻控制点分别沿其所在直线向中间控制点移动的距离。对于异号曲率连续转向,将转向处共线的三个控制点沿远离障碍物直角点的方向平移3。 在轨迹曲线无碰撞的基础上,判断轨迹曲线是否满足双轮自平衡机器人最大曲率约束,因此需要计算轨迹曲线的曲率。三次B 样条曲线的曲率可以按照如下公式计算: 其中三次B 样条曲线的一阶导、二阶导可由式(7)计算。取dK/du=0,可以求得曲率的极值点,判断其是否满足的约束,对于不满足最大曲率约束条件的区间进行优化处理。因A*算法搜索出的路径转向处为斜对角线的特点,所以轨迹曲线曲率极值点出现在控制点连线夹角γ≤90°处,故以γ=90°为界限对三次B 样条曲线控制多边形进行修改,来降低曲率。 为了分析控制点移动距离与曲率k 之间的关系,定义如下变量:β 为∠的角度,γ 为∠P1P3P5的角度,b 为的角度,h 为控制点P3到线段的距离,d 为线段的长度,h′为移动控制点P和P后控制点P到线段的距离,如图5 所243示。其中P2和P4分别为线段的中点,且和分别垂直于线段的。 图5 轨迹曲线调整Fig.5 Trajectory Curve Adjustment 对于B 样条曲线已经有一曲率估计公式被广泛认可[11],其计算公式为: 同理可得: 将式(11)~式(13)代入式(10)中可得: 由于A*算法搜索到的路径在进行180°转向时具有对称特性,故图5 中,简化式(14)得: 将双轮自平衡机器人最大曲率约束kmax代入式(15)中,可以求得控制点在沿垂直于原直线方向上移动的距离。 算法主要流程为:首先通过A*算法搜索路径生成线段性轨迹,将搜索到的路径点作为三次B 样条轨迹曲线的控制点,然后判断线段性轨迹的转向,对转向段添加中间控制点,并根据转向类型判断有无碰撞。若发生碰撞,则依转向类型移动控制点。其次判断控制点夹角γ≤90°,若满足条件,则添加kmax约束计算出控制点的移动距离,更新控制点。最后生成三次B 样条轨迹曲线,流程图,如图6 所示。 图6 算法流程图Fig.6 Algorithm Flow Chart 图7 轨迹曲线Fig.7 Trace Curve 图8 曲率曲线Fig.8 Curvature Curve 给出环境地图,依A*算法搜索最短路径,并以式(6)生成运动轨迹,如图7(a)所示。在转向处轨迹曲线存在碰撞点。根据式(9)计算出的轨迹曲线曲率,如图8(a)所示。曲率变化范围为[-1.45,0.5]。给定参数,双轮自平衡机器人重心高h=0.7m,两轮间距离 l=0.5m,重力加速度g=9.8m/s2,则曲率k∈[-4,4]。环境地图以1:5 的比例建立,则t=0.05。期望的轨迹曲线满足平滑、无碰撞和最大曲率约束三个条件。现以最大前进速度v=1.6m/s 为条件,根据式(5)计算得出的临界曲率k=1.36。添加中间控制点后轨迹曲线,如图7(b)所示。曲率曲线,如图8(b)所示。可以发现增加控制点后轨迹曲线曲率有所增长。利用基于无碰撞和最大曲率约束的轨迹优化方法后,轨迹曲线,如图7(c)所示。曲率曲线,如图8(c)所示。优化后的轨迹曲线并未与障碍物发生碰撞,且曲率范围调整到[-1.32,0.72],小于临界曲率k。 通过建立双轮自平衡机器人的运动学模型并分析受力情况,计算得出双轮自平衡机器人在运动过程中的最大曲率值。以A*算法搜索出的路径点作为三次B 样条曲线的控制点,生成运动轨迹。在此基础上,以给出的碰撞检测方法,判断轨迹曲线的碰撞情况,并推导出了控制点移动距离与轨迹曲线曲率k 之间的关系,并以此来控制轨迹曲线曲率,使其满足双轮自平衡机器人运动最大曲率约束条件。仿真结果表明,轨迹曲线平滑、无碰撞且曲率控制在最大曲率约束范围内。
3 运动轨迹平滑
3.1 三次B 样条轨迹曲线生成

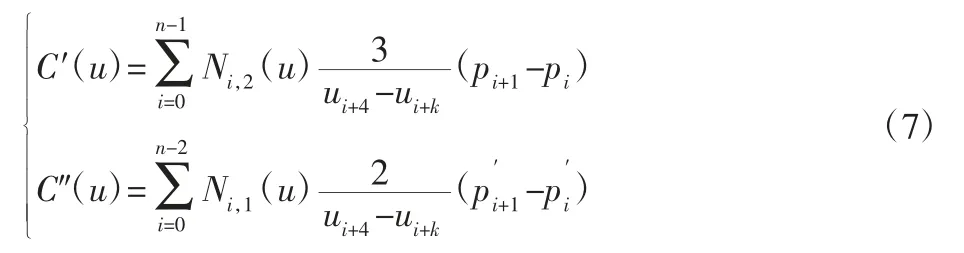



3.2 基于车身边界条件的轨迹碰撞检测

3.3 基于曲率约束的轨迹优化









4 案例分析


5 结论
