基于自适应遗传算法的大型关重件车间布局优化

张青雷 ，党文君 ，段建国

（1.上海理工大学机械工程学院，上海 200093；2.上海海事大学，中国（上海）自贸区供应链研究院，上海 201306）

1 引言

设备布局问题是现代制造业面临的一个非常重要的问题，为了全面的提高现代机械制造技术水平，提高机械产业的整体竞争力，降低车间内生产制造的生产成本，就需要合理的利用车间内的生产资源。而一个科学、合理的车间布置方案，就可以有效的利用车间内的生产资源，提高生产效率，还可以减少车间内的劳动及运输成本[1]。因此，科学合理的设备布局有着很重要的意义。

近年来，已经有不少学者[2-5]对车间布局问题有了比较深入的研究；文献[6]针对多零件族变批量的生产需求，分析了系统重用和加工任务重现的必要性，以重组成本、追加投资、空闲时间、加工任务重现度、系统重用度等指标为线性组合建立了目标函数，建立面向多零件族变批量需求模式的布局重组规划模型，用遗传算法进行求解；文献[7]分析了多品种小批量连杆类零件的生产特点及加工工艺，提出了一种柔性制造车间布局方法，通过选择柔性制造的加工设备及辅助设备，得出合适的车间布局方案；文献[8]针对面积不定、形状固定的多行布局问题，提出自由换行布局策略和净间距的概念，构建了带逆向物流的多目标组合优化数学模型，使用自适应遗传算法对模型进行求解；文献[9]以车间内物流搬运费用最小与空间利用率最大为目标建立多目标优化车间布局模型，并且提出一种差分元胞多目标遗传算法对车间内模型进行求解；文献[10]采用遗传算法针对某厂曲轴生产车间设备局部问题进行了优化研究，并提出了搬运矩概念，得到了较为优化的设计结果。但目前对于大型关重件生产车间的布局优化问题研究相对较少，关重件通常包括关键件和重要件，关键件是指具备产品关键特性的单元件，重要件是指不包含关键特性但是具有重要特性的单元件。一般大型关重件都是单件小批量生产，工件的体积较大且每道工序加工的时间较长。以大型船用曲轴这一关重件的加工车间为例，同时考虑物料搬运成本及搬运时间两个因素建立车间布局模型。对于标准遗传算法存在早熟收敛和后期进化缓慢的问题，使用一种改进的自适应遗传算法进行求解，有效的提高了整体寻优能力。

2 车间设备布局问题描述

2.1 问题描述及假设

对于大型关重件的生产车间，由于其单件小批量的生产特性，可将车间内的设备根据需要加工的零件的工艺计划将具有相似工艺特征的零件合并为一个零件族，然后将具有密切加工工艺关系的机器构建成生产单元，使单元零件的全部加工工序所包含的设备都在一个单元内，再对车间内各个生产单元进行多行布局[11]。假设车间内的生产单元的形状均为矩形块状结构，相互两个单元之间的物流运输方向只能平行于相应的参考线。设车间有n 个设备单元M=｛m1，m2，…，mn｝，布置为 r 行，引入一决策变量 Zik：

i=1，2，…，n；k=1，2，…，r；车间的长度为 L，宽为 H，车间内单元的长为S，宽为Q；将整个车间置入一直角坐标系中，行方向为x 轴正方向，列方向为y 轴正方向，生产单元的位置由其中心的坐标（xi，yi）确定。

图1 车间设备布局示意图Fig.1 Sketch Map of Workshop Equipment

2.2 确立目标函数

（1）车间布局的目标就是合理的提高资源的利用率，使得各设备单元间的总物料搬运成本最小化。因此，车间布局问题的数学模型可表达为：

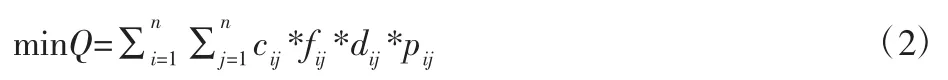
式中：Q—物流成本；cij—单位距离的运输成本；fij—单元间的物流频率；dij—单元间的距离单元间运输物料的重量。

（2）车间内的搬运时间主要有搬运距离、搬运频率与搬运速度有关，为优化车间布局，应使车间内搬运时间最短，其数学模型为：

式中：T—车间内总搬运时间；V—零件的搬运速度，取决于搬运设备。

（3）车间布局的总和目标函数为

式中：ωi—权重值，且 ω1+ω2=1 。

2.3 约束条件

2.3.1 行方向的约束

（1）每个生产单元只能布置在一个位置上且每行最多布置n个单元。

（2）同一行内任意两个生产单元之间的距离需大于基本间距Δx。

（3）同一行中单元布置不能超出车间范围

2.3.2 列方向的约束

（1）为使车间内生产单元布置较为整齐，同一行中单元的y坐标相同。

（2）在不同行中的任意两个生产单元在y 轴方向上的间距需大于基本间距Δy。

（3）在不同行中的生产单元在y 轴方向不能超出车间范围。

2.3.3 其它约束

影响车间布局设计的因素也有很多，除了上述设备尺寸与车间大小方面的约束条件及外，还包括其它很多特殊的要求约束。比如设备的搬运通道、人员的安全通道、参观通道等，或者车间内某些特殊位置的放置，这些约束具有一定的不确定性，为了简化工作，忽略这些特殊约束条件，建立了上述的优化模型。设计者可通过优化的布局并结合车间的实际情况得到最终的优化方案[12]。

3 基于改进自适应遗传算法的目标函数求解

标准遗传算法的基本思想起源于Darwin 的进化论和Mendel的遗传学说，是一种借鉴了“优胜劣汰”的生物进化法则和遗传思想提出的一种全局随机搜索算法。这种算法是将相关问题编码成为染色体，大量的染色体组成种群，通过不同的操作如选择、复制、交叉和变异等使得其初始种群不断进化，淘汰掉适应度值较低的方案，向着最优解接近。在标准遗传算法中，交叉率和变异率是影响遗传算法进化的关键，但是交叉算子和变异算子的数值是固定的，Pc和Pm数值的大小都会影响算法的收敛速度，可能会使算法的收敛缓慢或者是过早的收敛导致陷入局部最优。针对此问题，Srinvivas 等提出一种自适应遗传算法，根据个体适应度值的大小实时调整交叉、变异的概率，保持进化的优胜劣汰。

3.1 确定染色体编码方案

遗传算法通常都采用二进制编码方式，但二进制编码方式占用的存储空间比较大且需要较长的编码和解码时间，对于多行布局的车间问题，采用实数编码的方式。编码包括表示不同设备序列的符号和设备净间距两部分，采用如下的编码方式：

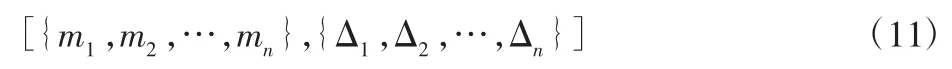
式中：｛m1，m2，…，mn｝—设备的排列顺序；｛Δ1，Δ2，…，Δn｝—第 i台设备与前一台设备的净间距。同时，采用自动换行的策略，即布置在同一行的设备的长度之和大于车间的长度，那么本行的最后一台设备将自动布置到下一行，继续新一行的布置。

3.2 适应度函数

种群的适应度是判断种群的个体优劣的依据，决定着种群中的个体繁殖或淘汰，算法在搜索过程中就是以适应度为判断的依据，车间布局的适应度函数可以采取目标函数值的倒数的策略实现，即。

3.3 产生初始种群

一般是由计算机随机产生N 个初设设备的排列序列及净间距组成初始种群，但为了加快遗传算法的收敛过程，使用目前车间真实的设备排列方式为初始种群中第一个染色体设备排列序号。

3.4 遗传操作

（1）选择运算。采用轮盘赌选择法，群体中的每个个体出现的概率都于个体的适应度值有关，其概率与适应度值的大小成正比，从而构成子代种群。（2）交叉运算。对于设备排列顺序采用部分匹配交叉算法（PMX）；对于净间距，采用算数交叉的方法。（3）变异运算。采用互换变异法对净间距进行变异操作。

3.5 自适应交叉、变异概率

遗传算法的交叉概率和变异概率能够对遗传算法的性能产生极大的影响，将会直接影响算法的收敛性。虽然M.Srinvivas 提出的自适应遗传算法的交叉率Pc和变异率Pm可以随适应度自动改变，但是当个体适应度等于或者接近最大适应度时，Pc和Pm等于或者接近于零，这对与算法的进化是不利的，使得变化初期种群内的优良个体基本不会发生变化，整个种群进化结果成为局部最优解的可能性增加[13]。因此，做出了一些改进：

式中：fmax—群体中最大的适应度值；favg—每代群体的平均适应度值；f′—需要交叉的两个个体中较大的适应度值；f—将要变异的个体的适应度值。算法改进后，当种群中的个体适应度值为最大时，其交叉率和变异率将不会变为零，其最优个体依然有概率继续进化，使得算法能够跳出局部最优解。

3.6 精英保留策略

为了避免交叉操作和变异操作破坏种群中的精英个体，保留每一代种群中的优良个体，采用了精英保留策略，精英保留策略的基本思想是种群进化过程中每一代适应度最大的精英个体直接复制到下一代，保证最优的个体不被交叉、变异等遗传运算破坏，精英保留策略也有效的提高了算法的收敛能力[14]。

4 应用实例

4.1 实例描述

应用上述的算法对某大型船用曲轴生产车间进行优化布局，车间长为264m，宽为72m。根据产品的工艺性，现将车间划分成的11 个区域，区域名称及面积，如表1 所示。车间的初始布局，如图2 所示。

表1 车间区域编号及面积（m＊m）Tab.1 Workshop Area Number and Area

图2 车间初始布局图Fig.2 Initial Layout of Workshop

一段时间内工件在各区域间的物流频率和物料运输的重量，如表2、表3 所示。由于船用曲轴各部分零件重量较大，车间内运输设备主要是使用天车和一种搬运平板小车进行运输。

表2 零件在各区域间的物流频率Tab.2 Logistics Frequency of Parts Between Regions

表3 区域间物料运输的重量Tab.3 Weight of Interregional Material Transportation

4.2 结果分析与比较

运用matlab 软件编写相应程序，对自适应遗传算法以及标准遗传算法进行运算。选取算法的参数，群体容量N=50，最大遗传代数为300，自适应遗传算法中Pc1=0.9，Pc2=0.6，Pm1=0.1，Pm2=0.01；标准遗传算法中Pc=0.6，Pm=0.1；以上述参数运用两种算法对问题进行计算。算法进化的过程，如图3 所示。对比两种算法的最优目标函数值，自适应遗传算法的优化程度明显高于标准遗传算法，达到最优解的进化代数也小于遗传算法，其收敛速度更快，克服了遗传算法收敛慢的弱点。

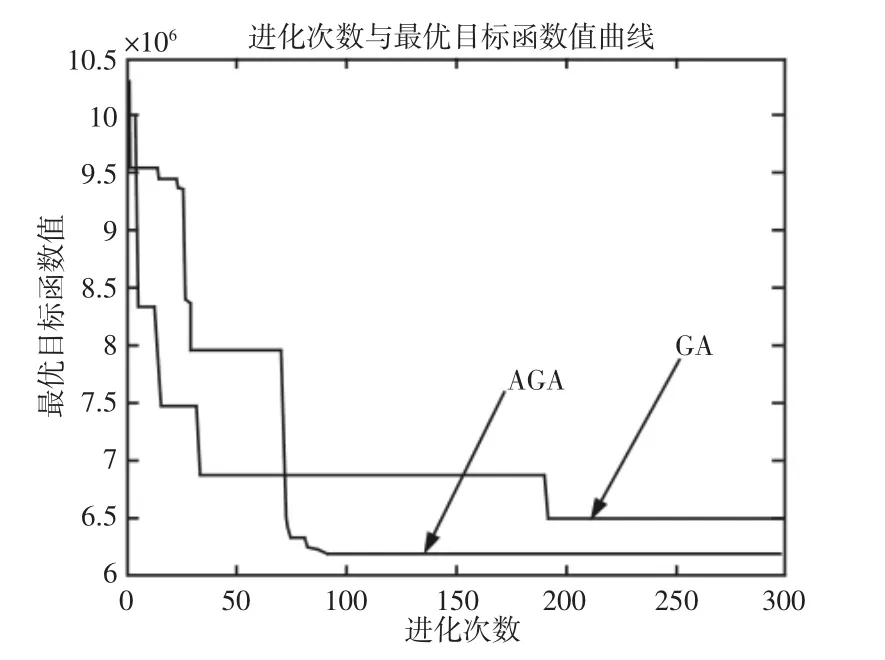
图3 遗传进化过程对比Fig.3 Comparison of Genetic Evolution Process

基于自适应遗传算法得出的车间布局的最优解为［10，9，7，3，4，8，1，2，5，6］，车间布局，如图4 所示。优化后的函数值由最初的10.1×106减小为6.2×106，优化后车间内的物料搬运成本与搬运时间比最初的布局减少35%，对车间内的生产效率有一定的提升。

图4 优化后的车间布局图Fig.4 Optimized Layout of Workshop

5 结论

（1）分析了大型关重件车间的生产特点，基于其单件小批量的生产特性，将有密切加工工艺关系的机器构建成生产单元，对各个生产单元建立了同时考虑物流费用与物流时间的多目标优化数学模型。（2）对于标准遗传算法存在早熟收敛和后期进化缓慢的问题，使用了一种交叉率和变异率可以随适应度自动改变的自适应遗传算法，采用自动换行的编码方式，并且加入了精英保留策略以提高算法的收敛能力。（3）通过实例验证了数学模型及自适应算法的可行性，车间内的物流搬运成本及物流时间节省35%左右，优化后的布局可以有效的提高生产效率，较好的实现了优化布局的目标。