一种花样机自然图案的缝制轨迹提取方法

周 军，廖晓波，朱建公

（西南科技大学制造过程测试技术省部共建教育部重点实验室，四川 绵阳 621010）

1 引言

当前缝制行业的缝制轨迹是由工程师通过游标卡尺等测量工具测量缝料的边缘尺寸，再利用CAD 等绘图软件绘制出缝制轨迹，最后再利用专用的图案生成软件生成可直接供工业缝纫机使用的花样文件[2]。但是，有许多待缝制的图案路径并不规则，各种曲线线条错综复杂，这给绘制CAD 的工程师增添了不少麻烦。因此，针对这一问题我们提出了一个基于机器视觉的缝制轨迹自动提取的算法。

2 花样机缝制轨迹提取概述

对图案的缝制轨迹进行提取，已经有很多比较成熟的方法。像最简单的图像边缘提取、图像轮廓提取等。但是传统的图像边缘原理基本都是图片里面像素值变化最大的地方的梯度，这就意味着使用这些方法提取出的线条包含太多噪声，同时也包含太多“断线条”。“断线条”在缝制过程中会出现不停剪线和跳针的情况，所以不适合用在缝制轨迹提取上。所以针对这一问题，很多学者研究一些算法是专门用来提取物体轮廓的，这大大减少了物体内的不必要的噪声线条的出现。这也为花样机的缝制轨迹提取提供了不少方便。比如文献[3]根据待提取目标的先验知识，提出了一种基于几何活动的轮廓提取方法，这种方法对目标提取比较有针对性，对于不同的目标识别性能不太好。文献[4]利用传统图像边缘提取的弱点，提出了一种基于灰度阈值的图像轮廓提取方法，这种方法抗干扰能力比较强，但是由于其是对单像素进行操作，对于缝制轨迹的提取会加入太多噪声。针对这一问题文献[5]以粒子滤波作为切入点，建立图像二维空间，以次来增加图像的信息利用率，提出了一种新的图像轮廓提取方法。这种方法确实有效缓解了轮廓提取中的绝大多数噪声，也比较适用于工程应用，但是算法复杂度较大，不太适合于实时领域。为了增强实时效果，文献[6]在图像的频域进行研究，针对城市道路中的绿灯进行优化，提出了基于频域的图像轮廓提取方法，这种方法实时性很好，但是算法运用比较局限。文献[7]针对实时视频监控领域，利用Douglas-Peucker 算法作为基础，采用图像目标轮廓质心的方式来提取目标轮廓，这在很大程度上消除了噪声的影响，并且也能达到实时性能要求。但是这种方法提取出的轮廓跟目标实际轮廓相差太大，不适用于缝制路径的提取。同时，国外也有许多轮廓提取的算法，如文献[8]提出了一种基于图像像素分类的轮廓提取方式，这向图像智能识别、智能提取方向迈进了一大步，但是这种算法由于需要事先进行训练，因此对于缝制轨迹提取不太实用。文献[9]为了快速准确的提取出图像目标轮廓，利用康普顿窗重新确定凸轮廓，这主要用于在医学图像方面，对于自然图像的轮廓提取也不是太好。针对自然图像的轮廓提取中，文献[10]利用Matting 原理提出了一种基于随机步长的图像分割方法，此方法能够很好地从自然图像中分割出所需要的目标边缘，但是由于采用的是步长的方式，轮廓边缘有非常明显的“阶梯”状，并且该算法耗时巨大，不适合利用在花样轨迹提取。

上述描述的方法在确实能够很好地提取出图像的轮廓，并且一些算法的实时性能也算良好。但是在缝制路径的提取中，要求图像是自然图像，这就意味着图像里面背景和目标相互交错，一般算法无法正确去除目标和背景。导致在自然图像轮廓提取中出现较大噪声，甚至根本无法提取其目标轮廓。针对这一问题，利用图像抠图理论[11]提出并实现了一种基于自然图像轮廓提取的算法。

3 图像目标提取算法

在数字图像处理领域和计算机图像学中，背景与目标用以下式子表达：

式中：Ii—获取的图像的像素值；Fi—获取图像中的目标像素（前景像素）；Bi—获取图像中的背景像素；α—目标像素的不透明度。在一张普通的自然图像中，上式右边全是未知量，而我们的任务则是要求出上式中的目标像素Fi，这也就意味着我们要将上式右边中的不透明度α 先求出。将上式变形得：

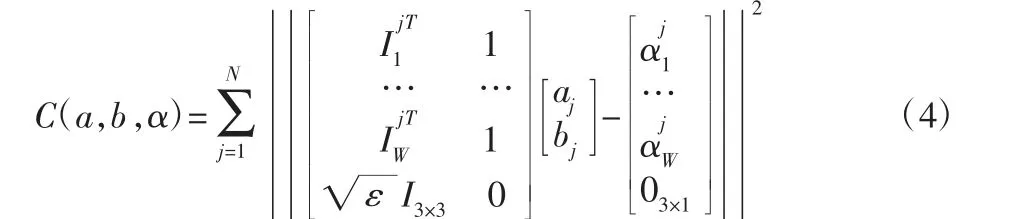
式中：W—在第j 个窗口中像素的总个数。于是有：

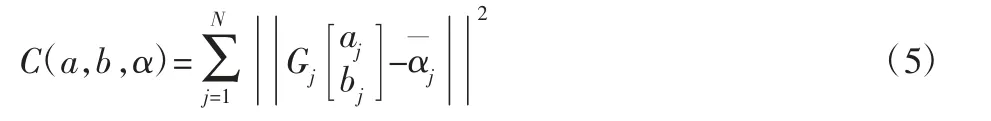
将式（6）回带入式（5）中，可以得到：

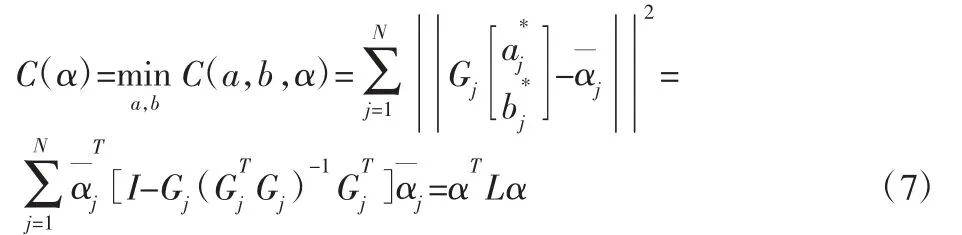
上式中的最后一项简化了所有矩阵，其中L（N×N）称为Matting Laplacian[11]（后文简称ML 矩阵）矩阵。经计算，它的通项为：

式中：μk、Σk—窗口 k 像素的均值和方差；δij—克罗内克函数。

通过定义我们可以知道，式（7）中的 L（i，j）是一个比较稀疏的矩阵。如果没有其他约束，要想从（7）求得唯一解，几乎不太可能。因此，我们必须依靠用户手工标注来表示已知的前景和背景像素，以此来约束（7）式的解。这样，问题就变成了：

将上式变形为：

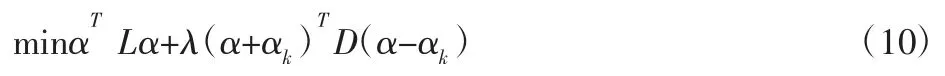
式中：αK—N×1 的向量，其值在前景像素位置为1，在其他位置为0；D—一个对角矩阵，他的对角元素在用户输入的位置为1，其他位置为1。λ—一个非常大的数，它主要是用来将用户输入强制与最终的解拉近。于是（10）式的求解就可以等效为：

从式（11）中我们便可求得唯一解。

4 基于Matting 的CRF 轮廓提取

4.1 CRF 中的特征函数的选取

通过式（7）可以知道，ML 矩阵L的特征向量其实就是不透明α 度的解，由于矩阵L有若干个特征向量，而且这其中大部分特征向量对于不透明度α 来说是没有意义的。由文献[12]可以知道，矩阵L 的最小特征值所对应的特征向量所包含的Matting 信息最为丰富，不同的特征向量代表不同的Matting 组分。因此我们可以将式（7）中的求最小值问题转换为如下约束优化问题：

其中E=［e1，…，eK］，分别对应ML 矩阵最小特征值所对应的K 个特征向量；式（14）表示在每个像素的所有Matte 组分之和必须为1。在式（12）中，由于我们最终得到的Matte 只有唯一的一个，因此其中的k=1，而ρ 的值定为0.9，因此式（12）可以变为：

式（15）便是最终选择的CRF 特征函数，其表示了在各个像素点α 的值对总的损失函数的贡献。

4.2 条件随机场（CRF）轮廓提取算法

要使用条件随机场[12]来智能获取目标轮廓，将图像模型抽象，如图1 所示。

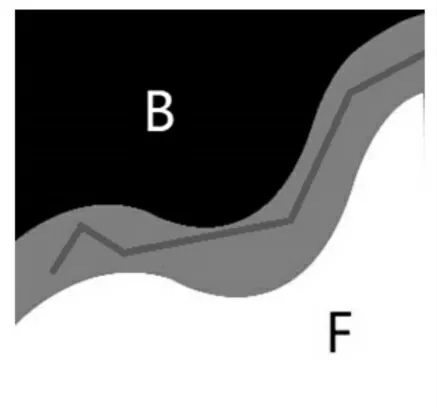
图1 基于Matting 的随机步长Fig.1 Random Step Based on Matting

从图1 中可以看出，轮廓线出现的位置只能是在背景和目标之间的位置，也就是0<α<1 的位置。轮廓提取的目标就是在0<α<1 之间众多的序列中寻找一条闭合的路径，并且这条路径必须要满足以下条件[2]：

（1）相应的锚点位置不能处于背景或者目标像素，并且锚点之间的连线不能与B 和F 有交集；

（2）路径的方向只能沿着B 和F 之间的区域，不能回旋；

（3）路径的选取要以包容目标像素为主，这样得到的路径才是准确的；

（4）尽可能的减少锚点数量，减少轮廓线的毛刺。

从上述条件中可以知道，这条路径并不唯一，但是在实现本算法的时候只要找到一条符合要求的路径就可以结束程序。于是针对某一条序列可以得到下式：

其中，p（l|s）定义为：

式中：l—具体某条序列（轨迹），而s 则代表在F 和B 之间所有的所带来的α 总的损失值。这样一来，通过极大似然估计法就可以求得最终的一条比较准确的轨迹。上式（16）跟logistic回归[13]的表达式基本一致，不过CRF 模型注重的是序列，换句话说式（16）其实就是逻辑回归的序列号版本。

实际上仅凭式（16）、式（17）是无法完成整个的轮廓的提取的。其中还有2 个未知量：带评定的序列（轨迹）和轨迹步长。

从式（8）所代表的矩阵中可以定以如下标记方向矩阵：

这其中的eij采用默认的方向进行初始化，vk则代表图像中边缘处的顶点。于是ML 矩阵L 可以利用矩阵A 来进行表示：

于是边缘处的狄利克雷积分表示为：

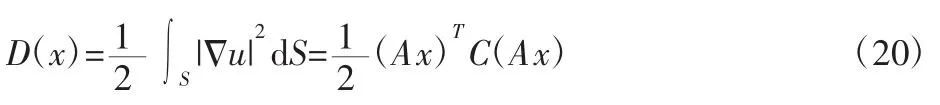
这个积分表示的是目标边缘向A 方向的所有像素点的集合。也就是式（16）中的序列。

5 实验结果与分析

算法的实现已经在Matlab 下完成，运行环境为windows 10企业版64 位操作系统。处理器为i7-7700HQ，4 核2.8GHz 主频。

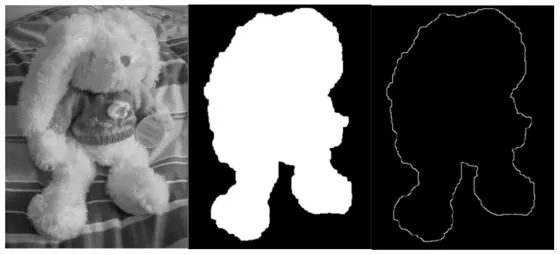
图2 算法结果Fig.2 Algorithm Results in this Paper

图3 边缘算子结果Fig.3 Edge Operator Result

从图2 和图3 中可以很明显看到，算法提取的自然图像中的目标轮廓相比使用常规的算子边缘提取方法要光滑很多，这使得工业缝制设备可以很大程度上加快缝制的速度。并且使用其他边缘提取算法所得到的目标轮廓中有许多孤立的点和孤岛存在，这是在缝制过程中不容许出现的。其中，利用文献[10]提取的轮廓，如图4 所示。

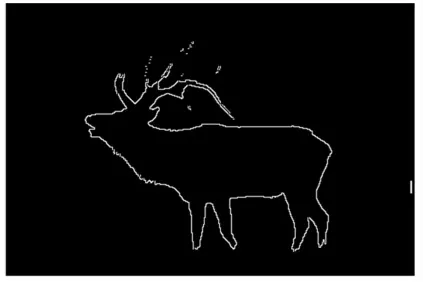
图4 文献结果Fig.4 Paper’s Results

从图4 中可以看出，利用文献[10]得出的结果中仍然具有孤岛存在，并且其中在图中牛的脖子部位有明显的梯度线条出现，如图5、图6 所示。

图5 算法结果Fig.5 Algorithm Results in this Paper

图6 左：文献；右：这里算法Fig.6 Left：Paper；Right：this Paper

梯度线条的出现会导致轨迹在缝制过程中方向突变，降低缝制效率。而这里算法在这些地方有明显改进，并且上图算法的运行只花了1.33s，而文献[10]却需要2.14s，速度提升了近40%。

为了体现这里算法速度的提升，在测试的时候分别利用大小为 300×300、400×400、500×500、600×600 以及 720×600 的图片分别运行5 次进行测试，结果如表1 所示。

表1 算法时间对比 单位（s）Tab.1 Algorithm Time Comparison

从上面中可以看出，这里算法在经过优化后与文献[10]相比能够整体提高31%左右。

算法的一些其他例子：

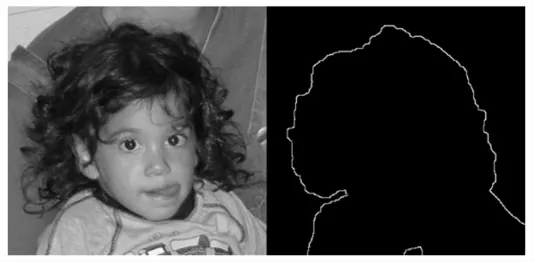
图7 这里算法示例2Fig.7 Example 2 of this Algorithm

图8 这里算法示例3Fig.8 Example 3 of this Algorithm

从上面示例中可以看出，这里算法在处理自然图像缝制轨迹（轮廓）的提取上具有良好的作用效果，相比目前成熟的边缘提取算法、轮廓提取算法而言具有较强的专一性。另外，自然图像由于背景复杂，因此在目标的选取中需要有人工参与，即采用大致标注的方式将目标像素和背景像素区分，这样使得这里算法具有较强的适应性。并且这里算法运行速度大大提升，使得算法的应用范围更加广泛。

6 结论

基于自然图像的Matting，构建CRF 模型，提取出自然图像中目标的轮廓线。由于工业缝纫机对于缝制轨迹的要求较高，所以传统的边缘提取算法和轮廓提取算法显得无能为力。其主要原因是传统的边缘提取和轮廓提取算法几乎都是依赖于像素与像素之间的差异而开发的算法，因此所提取出的轮廓过于“精确”，导致提取出的轮廓线噪声太多，不满足工业缝纫机的缝制要求。因此提出的这种算法专门用于解决这种问题的出现。实验结果表明，提出的算法对于自然图像的目标轮廓提取方面具有较强的适应性，并且提取出的轮廓较为光滑，无“孤点”、“孤岛”的现象存在，非常适用于工业缝纫机的缝制轨迹。但是这里算法也有一定不足，就是由于算法计算量大，导致算法运行时间依然很长，如需应用到实时领域，还需要对算法进行优化。