抽样改进加权核大数据谱聚类算法

申 锐，吴 睿

（1.山西交通职业技术学院，山西 晋中 030600；2.西安交通大学软件学院，陕西 西安 710061）

1 引言

随着科技与互联网的发展以及信息传输量的急速提高，以大数据为主要特性的网络结构日益凸显出来，TB 甚至PB 级的海量信息数据已经成为常态。但是网络在方便我们日常工作和丰富我们生活的同时，如何提取有价值的知识显得尤为重要。聚类能够根据数据特征，将相似特征数据进行归类，从而高效组织数据[1]。现有k-means 等聚类算法依赖于初始值的选取，并且基于欧氏距离和梯度下降进行的搜索常常使算法陷入局部最优，而基于非线性核距离且对任意形状样本集都具有全局最优解的谱聚类，成为近年研究热点[2]。

但是，传统的谱聚类算法涉及构造相似度矩阵和对相应的拉普拉斯矩阵特征分解，需要的空间复杂度和的时间复杂度对于大规模数据集来说是难以承受的计算负担[3]。为此，文献[4]通过计算数据的低维嵌入，提出基于拐点估计的谱聚类中心数自动确定方法，对分布复杂数据集的谱聚类效果较好；文献[5]通过在选取的核心点集上分组和谱聚类，并根据数据集与核心点集的一致性实现大数据谱聚类。文献[6]提出使用Nystro¨m 近似技术来避免计算整个相似性矩阵，加速大数据谱聚类；随后文献[7]又用近似奇异值分解方法提升了Nystro¨m 方法中特征分解的效率；而文献[8]则设计了一种自适应采样的方法，改进了Nystro¨m 谱聚类的聚类效果。文献[9]根据 Nystro¨m 误差界分析，采用集成Nystro¨m以牺牲数据计算准确性换来大数据谱聚类的快速计算，具有更快的收敛速度。为避开矩阵特征分解的时间复杂度，文献[10]在研究加权核k-means 算法与谱聚类Normalized Cut 目标函数在数学上等价基础上，通过加权核k-means 算法优化，取得了更好的聚类结果。但其在有效捕捉非线性数据结构的同时，还需存储一个较大的核矩阵；文献[11]提出了基于地标点的谱聚类算法，指出该方法适用于大规模数据集，并且性能要优于Nystro¨m 方法，并在随后给出了相关理论分析，但该方法用随机采样确定地标点，抽样结果不稳定。

随机映射由于可在降低数据规模的同时保持大部分原始信息而被广泛用于聚类算法中，为此在已有加权核k-means 与经典谱聚类等价方法的研究基础上，利用随机映射得到近似奇异值分解，然后由分解得到的近似奇异向量确定各点在数据集中的权重并计算抽样概率，以此得到快速合理抽样，然后通过约束随机抽样的样本点生成的子空间来逼近聚类中心，从而仅需要计算部分核矩阵即可实现大规模谱聚类，极大减少核矩阵的复杂度，实验验证了改进算法与标准算法具有相近的聚类表现，但极大缩短运行时间。

2 加权核k-means 与谱聚类等价性

2.1 经典谱聚类

谱聚类基于谱图理论，将待分析大数据作为无向加权图进行处理，从而将聚类问题转变为子图内权值最大而子图间权值最小的最佳图划分问题[2]。将 n 点数据集 X=｛x1，x2，…，xn｝视为无向图G，则将X 聚类为k 类即为将V=X 划分为k 个子集，即且Vi∩Vj=ø，i≠j。谱聚类应使其划分所得类的类内连接权值最大，或类间权值达到最小值，由此得到谱聚类的目标函数。建立类别矩阵描述 V 中元素是否属于类Vi，即对于节点 xi，若 xi∈Vi，则 Uij=1，否则 Uij=0，根据节点类别的唯一性，有UT1k=1n，向量1n∈Rn×1的元素全为1。则谱聚类目标函数可写为[11]：

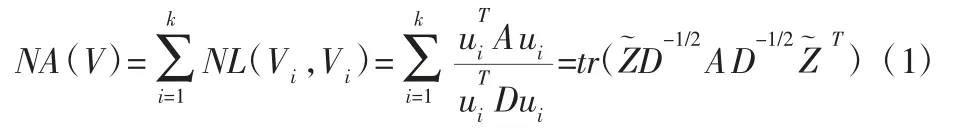
式中：NL（V1，V2）=L（V1，V2）/L（V1，V）—两个子类间总的归一化连接边权值—描述了子类Vi内元素的连接权值ZD1/2且满足约束是单位矩阵，tr（·）表示矩阵迹[11]。

2.2 加权核k-means 算法

核k-mean 算法采用非线性核距离度量[12]。对核k-mean 算法的每个数据xi都分配一个权值wi，得到加权核Kmeans 算法的目标函数：

式中：κ（，）：Rd×Rd→R—核距离函数；Hk—再生核希尔伯特空间，的泛函范数；ci（·）—第 i∈［k］聚类中心，则由权值 W=diag（w1，…，wn）可以构建待聚类集合的加权类别矩阵Y=（y1，…，yk）T=UW及，其中则加权核k-means 最佳的类中心为[12]：

将式（2）目标函数平方项展开，写为矩阵迹的形式得

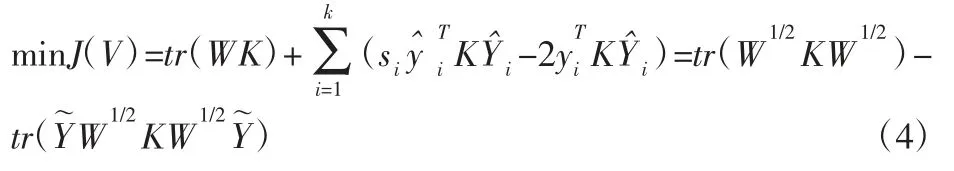
式中：K∈Rn×n—核距离函数矩阵，Kij=κ（xi，xj），由于式第一项为常量，比较式（1）和式（4）可见，Normalized Cut 目标函数基于矩阵迹与加权核k-means 是等价的，因此可以通过加权核k-means 算法的迭代计算解算NA（V）目标函数，替代矩阵特征分解的高复杂度计算。加权核k-means 算法进行大规模数据谱聚类，在时间和空间复杂度上均有很大优势，并且在聚类效果上也令人满意，但式（4）仍需计算全部核矩阵K，在大规模数据集应用时仍受限。为此，通过随机抽样部分数据构建部分核矩阵，并约束样本子空间以涵盖聚类中心，设计了改进加权核k-means 算法进行大数据谱聚类。

3 抽样改进加权核k-means 算法

根据式（3），聚类中心为类内所有数据的线性组合，即其位于类内数据张成的子空间中，ci（·）∈Hκ，因此，如果采样数据能够把类中心约束到其张成的较小的子空间⊂Hκ，且满足（1）尽可能的足够小；（2）具有足够覆盖空间以近似的聚类结果，则可以通过采样数据获得与原数据相似的聚类效果。为此，文中首先给出基于随机映射的快速数据抽样，在合理抽样基础上给出构造的方法以改进加权核k-means 算法的复杂度。

3.1 基于随机映射的快速数据抽样

作为抽样改进加权核k-means 算法的关键，抽样点的选取在很大程度上影响了改进算法的聚类效果。常用的方式是均匀随机采样，但在大规模数据集上随机抽样的不稳定性很可能会导致所抽样本点集中于某一区域。为此，采用基于随机映射的近似奇异值分解（Singular Value Decomposition，SVD）算法[13]，在降低采样过程时间复杂度的同时，得到与精确SVD 相近的采样结果，快速数据抽样算法，如表1 所示。

表1 基于近似奇异值分解的快速数据抽样Tab.1 Fast Data Sampling Based on Approximate SVD

根据表1 算法产生抽样所需的抽样矩阵S，通过STA∈Rp×d可实现数据抽样。根据文献[14]中定理，基于该抽样所得到的矩阵A∈Rn×d的行样本，其最优近似误差与相差一个较小的因子，保持了原始矩阵的大部分信息，即对任意矩阵抽样并适当调整样本尺寸后，所产生的矩阵与原始矩阵在Frobenius 范数平方上接近，从而表明，采用基于近似SVD 的抽样可以保证抽样误差在特定的界内，这使得采样的样本具有较好的代表性。因此，利用该方法所得到的采样样本，其与数据点形成的相似度矩阵能较好地描述数据之间的关系[14]。

3.2 基于改进加权核k-means 的谱聚类

4 实验与分析

为验证文中算法（记为Sik-SC）性能，将其与经典谱聚类（Clas-SC）[15]、基于标准加权核的谱聚类（Swk-SC）[11]、基于 Nystro¨m谱聚类（Nys-SC）[8]和基于 MEKA 近似核聚类（Mek-KC）[7]四种谱聚类方法进行性能比较实验。实验环境：Intel（R）CoreTMi7-4710MQ@2.50GHZ，16G 内存，MATLAB 2016b，数据集部分重要参数，如表2 所示。

表2 实验数据集参数Tab.2 Data Characteristics of Benchmark Datasets

Ringnorm 集[15]MNIST 集为含有10 种类型的手写数字图片集；MNIST 集为含有10 种类型的手写数字图片集[16]；实验中聚类结果的准确性采用归一化互信息来评价：

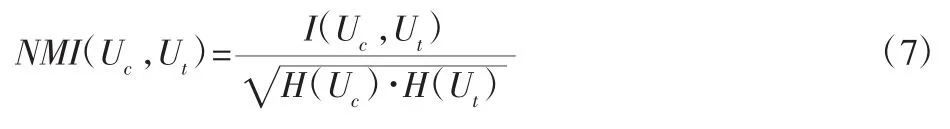
4.1 聚类性能比较实验

Nys-SC、Mek-SC 和 Sik-SC 算法在 4 个数据集上 NMI 结果，如图1 所示。由于Clas-SC 与Swk-SC 对所有数据进行处理，即采样率为100%，因此其在Ringnorm 数据集上的NMI 指标为0.3758 和0.3895，而在MNIST 集上，由于数据规模巨大，数据维数较高，两算法没有实现聚类。

图1 算法在各数据集上的性能实验结果Fig.1 Performance Results on Various Data Sets

从图1 结果可见，通过数据抽样，Nys-SC、Mek-SC 和Sik-SC算法在2 个数据集上都表现出较好的聚类性能。且随着采样点数的增加，三种算法的聚类NMI 指标逐渐增大，聚类性能逐渐提高。将图1 结果与Clas-SC 与Swk-SC 两种算法的实验结果对比分析，Sik-SC 算法在不同采样率下的NMI 指标与Clas-SC 和Swk-SC 算法的NMI 指标相关不大，而随着采样点数的增加，Sik-SC 算法的聚类NMI 指标逐渐逼近Swk-SC 算法的聚类NMI指标，说明文中改进加权核k-means 算法通过将聚类中心约束在采样数据张成的子空间的改进方法可以取得与使用完整核矩阵相近的聚类结果，也说明改进方法有效。

4.2 算法运行时间比较实验

Nys-SC、Mek-SC 和Sik-SC 算法在不同采样时的运行时间结果，如图2 所示。Clas-SC 算法与Swk-Sc 算法在Ringnorm 数据集上的运行时间分别为247.4842（s）和 157.67012（s），而在 MNIST集上因无法实现聚类，其运行时间未知。

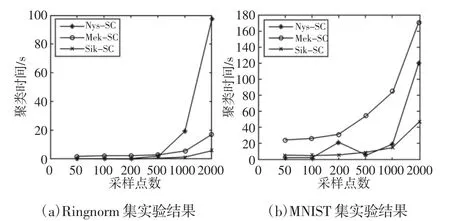
图2 算法在各数据集上的运行时间Fig.2 The Running Time of the Algorithm on Each Data Set

从运行时间比较实验结果可以看出，Clas-SC 算法聚类所需要时间最长，主要是因为其完整的Laplacian 矩阵特征分解过程的时间复杂度最高，而Swk-SC 算法采用加权核kmeans 算法替代矩阵特征分解，聚类效率有了明显的提高，但其全部核矩阵的使用在数据规模巨大时，无法得到聚类结果，而仅使用部分核矩阵的Nys-SC、Mek-SC 和Sik-SC 算法在所有数据集上的运行时间都得到大大幅度的缩减，且在MNIST 集上仍取得较快的聚类运行时间。从图2 三种算法的实验结果可以看出，随着采样点数的增加，抽样率改进聚类效果的同时三种算法的聚类时间也逐渐增加，但Sik-SC 算法的变化趋势相对最为缓慢，且大多数情况下聚类时间较短，这主要因为，随着抽样点数的增加，同样采用抽样策略的Nys-SC 算法，其近似特征向量的计算时间大幅增加，而Mek-SC 算法的最佳k 秩近似核矩阵的求解效率也会大幅降低，Sik-SC 算法仅与采样点数及迭次数相关，因此在采样数增大时，能够较缓慢的增长趋势，聚类效率更高。

综合实验结果可以看出，Sik-SC 算法在保持与经典Swk-SC算法聚类性能相似的情况下，极大的提高算法的聚类效率，更适合大规模数据挖掘工作。

5 结语

在分析经典谱聚类算法与加权核k-means 函数等价的基础上，设计了一种基于抽样改进加权核k-means 的大规模数据谱聚类算法，算法通过加权核k-means 优化迭代过程避免Laplacian矩阵特征分解的高复杂度资源占用，通过随机映射得到近似奇异值分解，并由分解得到的近似奇异向量确定各点在数据集中的权重并计算抽样概率，以此得到快速合理抽样，通过约束抽样子空间以涵盖聚类中心，避免全部核矩阵的使用，从而降低经典算法的时间空间复杂度。实验结果表明，改进算法在保持与经典算法相近聚类精度基础上，大幅提高了聚类效率。但是改进算法还需进一步考虑如何合理设置采样数以提高算法的性能。