基于刚柔耦合模型的卫星成像仪多工况强度分析
2021-01-27费振南范让林冯程程
费振南,范让林,冯程程,殷 芳
(北京科技大学机械工程学院,北京 100083)
1 引言
刚柔耦合多体动力学可以解决刚体和柔性体耦合系统大范围运动的动力学问题,相比于多刚体动力学,进一步考虑了柔性体的变形对刚体运动和系统运动的影响,是多刚体动力学的发展与延伸。刚柔耦合多体动力学能够考虑柔性体弹性变形对物体运动的影响,在航空航天[1-4]和车辆[5-6]动力学领域应用较为广泛,同时也应用于故障诊断[7]和疲劳分析[8-9]。
相比通过ANSYS 等有限元软件进行瞬态工况的强度分析,刚柔耦合模型子结构模态综合法因缩减了求解规模,导致其分析耗时较短。
某卫星成像仪在火箭发射过程中受到随机、正弦扫频和冲击激励,当该子系统分别受到这三种激励时,分析该子系统主体结构的强度。基于改进Craig-Bampton 方法,用有限元法将成像仪主体结构离散柔性化,并将依附于主体结构之上的其他附件视为刚体,结合多体动力学理论,建立系统的刚柔耦合模型。分析成像仪在多工况振动激励下,主体结构等效应力最大的位置,并根据模态参与因子优化结构,降低最大等效应力,使其满足强度要求,并满足总质量限值。
2 子结构模态综合法
2.1 子结构模态综合法的步骤
用有限元对柔性多体系统建模,其优越性在于任何复杂系统均可用恰当的有限单元组集进行模拟。为了避免系统通过直接采用节点坐标描述柔性体而产生的庞大自由度数,在满足工程精度的条件下,引入结构动力学的模态综合技术,通过模态坐标作为广义坐标缩减系统方程的自由度,降低求解规模。
子结构模态综合法繁多,但分析步骤大致相同[10]。首先将整体系统分割成若干个子结构,建立子结构的模态集和模态坐标。子结构ψ 模态集主要包含主模态φn、约束模态ψc和附着模态ψa,一般表示为:ψ=[φnψcψa]。
子结构物理坐标与模态坐标之间的关系式为:

式中:u—物理坐标;p—模态坐标。
其次,利用子结构界面的连接关系产生协调方程,建立各子结构之间的联系,通过坐标变换矩阵S 把所有子结构各自独立的模态坐标p 变换到系统广义坐标q 下:

从而得到系统在广义坐标下的动力学方程。最后求得该动力学方程的解,经过式(1)和式(2)两次坐标变换,返回到物理坐标u,求得所需的解。
2.2 改进的 Craig-Bampton 法
各种模态综合法的共同特征是在保留子结构主模态的同时,再增补各种静力相关模态,构成一个完备的模态参数与系统的综合;主要差别是选取的静力相关模态的不同以及由于界面约束形式不同而导致二次坐标变换矩阵S 的不同。
固定界面模态综合法中Craig-Bampton 模态分析法不适用于部件有大范围刚体运动的情况[11],且得到的分支模态集不能与频率相对应,难以进行动力学分析。在Virtual.lab Motion 中采用改进的Craig-Bampton 法,以适用于多体动力学系统仿真。其选择的是分支模态集,包含固定界面的子结构保留主模态与对全部界面坐标的约束模态。改进前后的模态坐标之间的关系,如式(3)所示。改进后的物理坐标与模态坐标之间的关系,如式(4)所示。

式中:s—模态阶数;r—改进后的模态坐标;Ns=[n1L ns]—所需前s 阶频率对应的正则化模态;ψ—传统Craig-Bampton方法求得的分支模态集;φ—正交Craig-Bampton 模态。固定界面模态综合法将子结构组装成整体时,需满足界面位移协调条件和界面力的平衡条件。
3 刚柔耦合分析流程与模型建立
3.1 刚柔耦合动力学分析流程
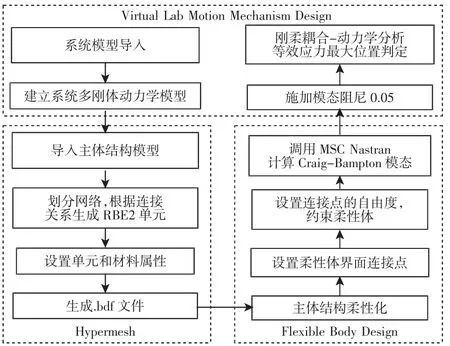
图1 刚柔耦合分析流程Fig.1 Process of Rigid-Flexible Coupling Analysis
通过Virtual.Lab Motion 模块建立结构的多刚体动力学模型,在Hypermesh 中对主体结构进行网格划分,建立有限元模型。将网格模型导入将动力学模型中,使主体结构变为柔性体,设置连接点,并通过Flexible Body Design 模块调用MSC Nastran 进行模态分析,最后进行刚柔耦合系统动力学分析,具体建模流程,如图1 所示。
3.2 刚柔耦合模型的建立
卫星通过四个支承结构与成像仪子系统连接,并传递加速度激励,如图2(a)所示。成像仪系统内部结构复杂,与众多电子元件和机械结构相连。在建立多刚体动力学模型时,将内部其他附件视为刚体,并根据连接关系施加各附件与主体结构之间的运动副。在有限元软件中离散主体结构时,需根据主体结构与各刚体连接点和接触面设置RBE2 单元。
结构材料为 2A12,材料参数为:E=68000MPa,μ=0.33,ρ=2.78×10-9t/mm-3,σ0.2≈256MPa,σb≈410MPa,如图2(b)所示。主体结构有限元模型共有237640 个单元,73166 个节点。
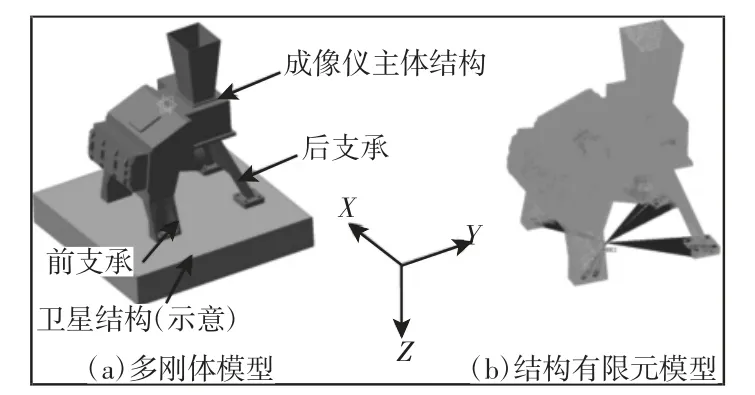
图2 子系统多刚体模型及主体结构有限元模型Fig.2 Multi Rigid Body Model of Substructure and Finite Element Model of Major Structure
将成像仪主体结构视为子结构,并做柔性化处理,设置刚体和柔性体的连接点与自由度,调用MSCNastran 求解结构的Craig-Bampton 模态,去除前六阶刚体模态参数,得到结构的分支模态集。
模态阻尼设为0.05,以加速度激励信号作为驱动施加在成像仪主体结构与卫星的连接点处,应用子结构模态综合法进行刚柔耦合系统的动力学分析。
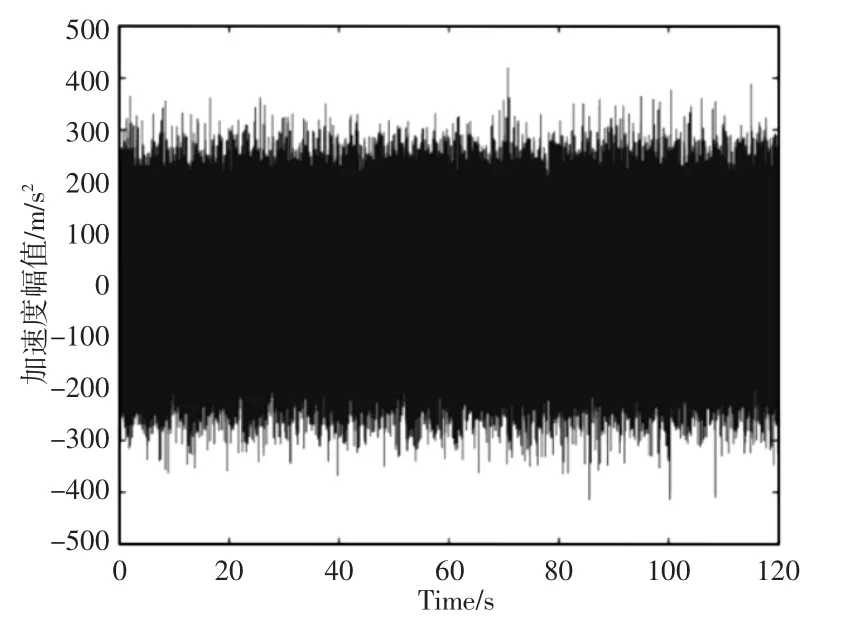
图3 随机激励时域信号Fig.3 Time Domain Signal of Random Excitation
在卫星与成像仪连接点处施加三种激励,如图3~图5 所示。三种激励的频率成分各不相同。将各工况激励依次施加在连接点的X、Y、Z 方向,获取三种工况下的主体结构最大等效应力与其位置,进行结构强度校核。
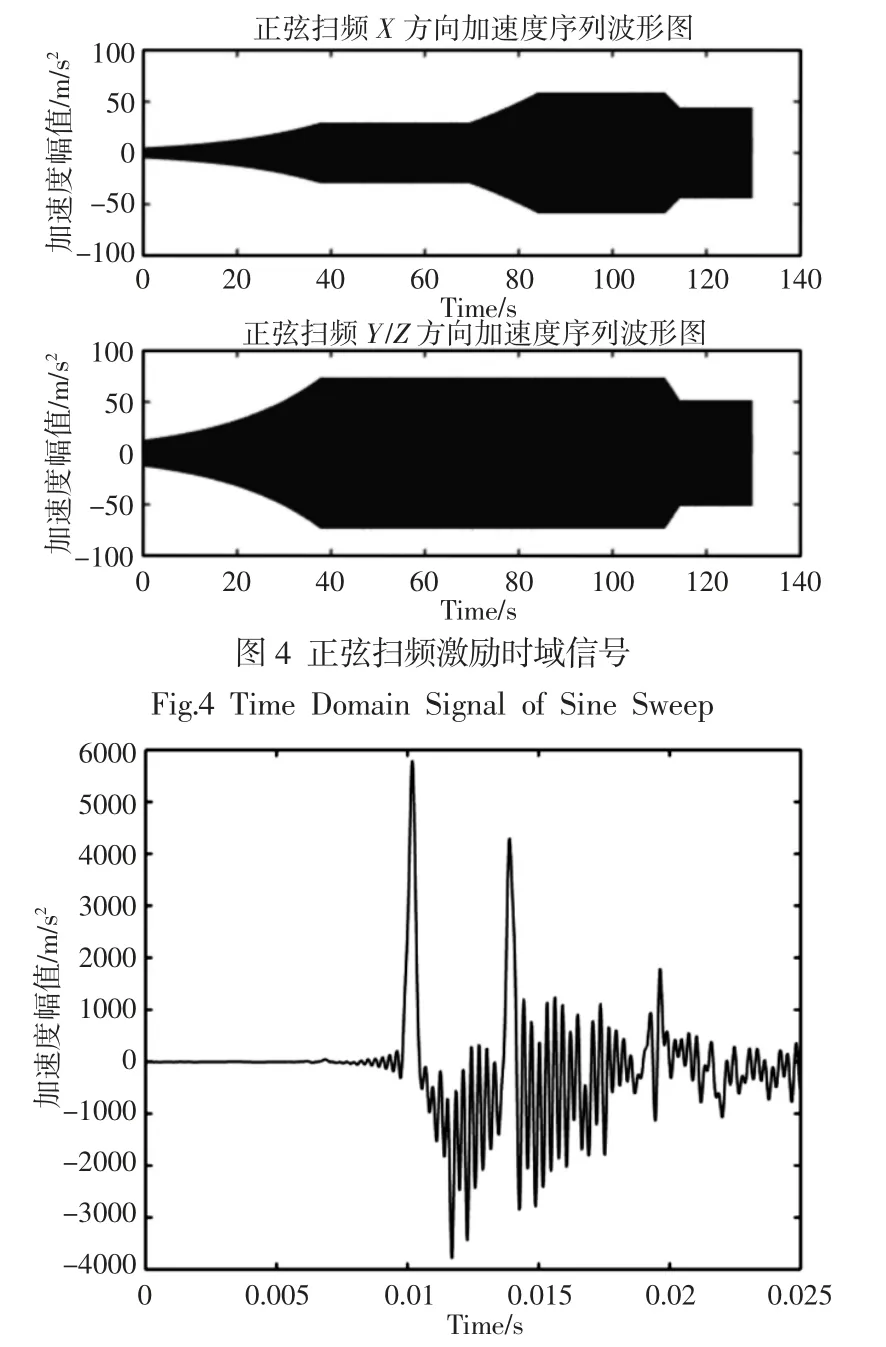
图5 冲击激励时域信号Fig.5 Time Domain Signal of Impact
4 仿真结果分析

图6 X 向冲击激励下结构等效应力云图Fig.6 Von Mises Stress Cloud Image of Structure Under X Impact Excitation

图7 随机激励下结构等效应力曲线Fig.7 Von Mises Stress Curve Under the Random Excitation
通过卫星主体结构在三种工况下的von Mises 应力云图,综合判断结构最大等效应力的位置,并以该位置周围若干节点等效应力的平均值衡量等效应力大小。分析结果表明,三种工况下的结构最大等效应力位置均在前支承的2 个螺栓连接处,以X 向冲击工况下某时刻结构的等效应力云图为例,如图6 所示。各工况作用下最大等效应力,如图7~图9 所示。

图8 正弦扫频激励下结构等效应力曲线Fig.8 Von Mises Stress Curve under Sine Sweep Excitation
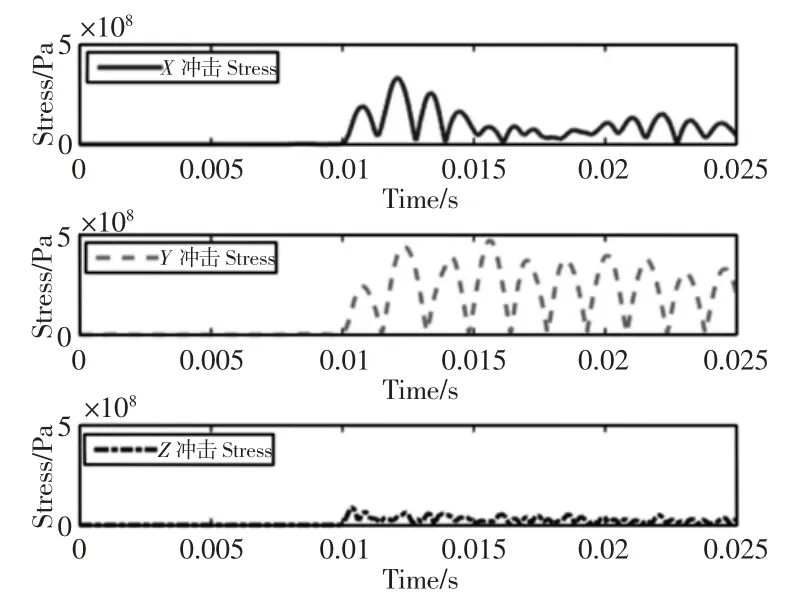
图9 冲击激励下结构等效应力曲线Fig.9 Von Mises Stress Curve Under Impact Excitation
根据以下各工况结构等效应力结果可知,各工况的X 和Y向激励下的最大等效应力大于Z 向激励;随机与正弦扫频工况的等效应力小于屈服极限,满足强度要求;但冲击工况下X 和Y 向等效应力结果远大于材料的屈服极限,在工作状态下成像仪主体结构会发生失效,不满足强度要求。
5 基于模态参与因子的结构强度优化
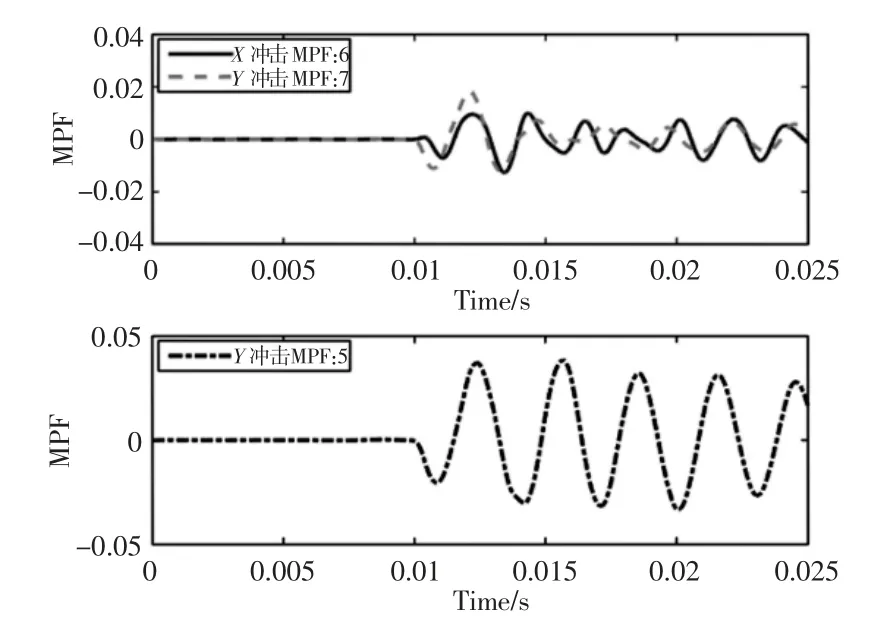
图10 X 和Y 向冲击激励下最大模态参与因子Fig.10 Maximum MPF Under X and Y Impact Excitation
当成像仪受到加速度激励时,可以通过模态参与因子(MPF:Modal Participation Factors)衡量各阶模态参与结构响应的大小。该优化过程以降低成像仪结构体在冲击工况下的最大等效应力为优化目标,以最大模态参与因子的模态振型位移大小为约束条件。具体方法为通过增强结构在该阶模态的局部刚度,减小结构在响应中变形,进而降低等效应力。基于刚柔耦合模型分析结果,X 和Y 向冲击工况下主体结构最大等效应力不满足屈服强度的要求,提取两次分析中结构的MPF 最大的模态,得到该阶模态的MPF 随时间变化曲线,如图10 所示。由图可知,X 向冲击激励作用时,第6、7 阶模态参与因子较大;Y 向冲击激励作用时,第5 阶模态参与因子较大。
模态振型,如图11、图12 所示。主体结构第6、7 阶模态振型主要为结构前支承X 向变形,第5 阶模态振型主要为结构前支承Y 向变形。据此可知,在X、Y 向冲击工况作用下,由于结构前支承X 和Y 向抗弯刚度不足和与卫星连接点过少,导致结构局部抗弯刚度不足,使前支承在响应过程中变形较大,进而导致前支承与卫星连接的螺栓孔处等效应力超过材料的屈服极限,不满足强度要求。
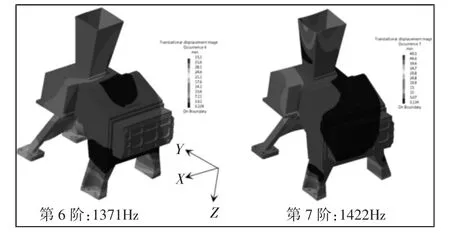
图11 第6 和7 阶模态振型Fig.11 The 6th and 7th Modal Shapes
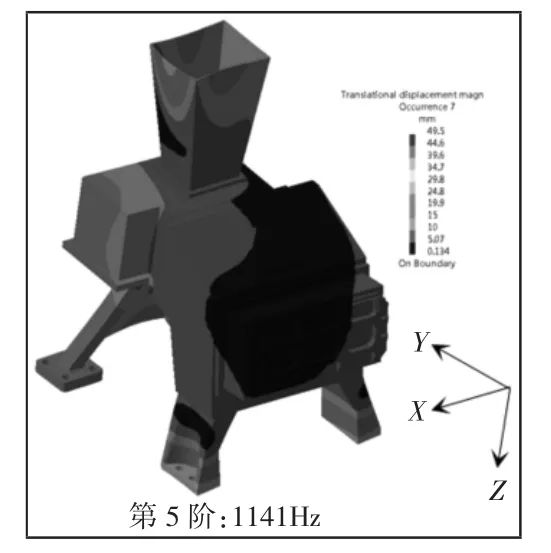
图12 第5 阶模态振型Fig.12 The 5th Modal Shape
根据模态振型可知,增加支承结构的刚度可减小结构在激励响应中的变形,提升结构强度。增加连接前支承X 向厚度和连接点个数,可增加其抗弯刚度和连接刚度,减小结构最大等效应力,结构优化结果,如图13 所示。
图13 优化后的主体结构Fig.13 The Optimized Major Structure
将优化后的主体结构重新进行离散化,并建立成像仪刚柔耦合模型,进行各工况下的动力学分析,提取主体结构的最大等效应力及位置,得到其等效应力随时间变化曲线。由分析结果可知,优化前后结构强度的最大等效应力位置不变。对比优化前后最大等效应力,如图14 所示。由图可知,优化后结构在冲击激励作用下的最大等效应力大幅降低,并在整个冲击过程中均小于屈服应力,处于安全区间,满足强度要求。
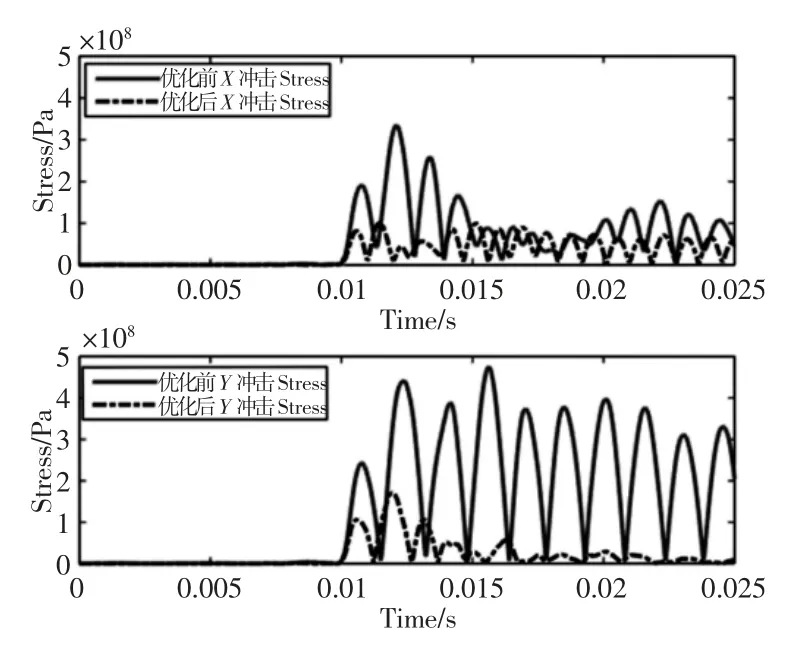
图14 优化前后最大等效应力对比Fig.14 Maximum Von Mises Stress Comparison of Structure Before and After Optimization
6 结论
(1)基于Virtual.Lab Motion 的刚柔耦合多体动力学模型,利用子结构模态综合法,分析结构在动态环境下的强度,该方法能够考虑系统内部结构的运动对结构变形的影响,仿真边界条件接近真实状态,分析结果更加准确且有效。
(2)对于不满足强度要求的工况,基于模态参与因子进行结构优化,通过比较该工况下的模态参与因子大小,提取参与系统响应最大的模态,增加该阶模态振型最大变形处的结构刚度,减小其变形幅度,进而有效降低最大应力,使结构满足强度要求。
