气体静压径向轴承气膜流场及承载特性分析
2021-01-27高尚晗徐武彬
范 酬,高尚晗,李 冰,徐武彬
(广西科技大学机械学院,广西 柳州 545000)
1 引言
相对于传统的油膜润滑轴承,气体静压径向轴承具有回转阻尼小、工作精度高、使用寿命长等诸多优点。广泛地应用于电子产品制造、交通运输、能源以及航空航天国防工业等技术领域。针对气体静压轴承在静态性能方面存在的承载力小和刚度低等问题,在气体动力学理论基础上,文献[1]利用扰动法提出了提高无限长气膜区间承载力的一种解决方案,并实现计算精度的提高。文献[2]通过实验验证了气体静压径向轴承承载力、转子旋转不稳定性和阻尼系数之间的关系,并通过扫描旋转频率的范围来确定稳定性的极值。文献[3]在研究轴承不稳定性时发现,当存在偏心时,转子会由于压力的不平衡而引起旋转的不稳定性,进而引出了偏心率对气体静压径向轴承稳定性的研究。文献[4]采用有限差分法求解连续性方程和修正雷诺数方程,研究参数条件下静止和旋转轴颈的稳态承载性能,并提出外部加压多孔气体径向轴承的理论设计方法。文献[5]通过实验分析节流孔的个数对气体轴承的影响,指出单排节流孔数量应≥5,以防止相邻节流孔之间的压力分散而造成的承载能力下降。文献[6]采用数值计算方法来研究不同类型的节流孔对承载力的影响,并采用实验方法验证理论计算的可行性。
为进一步提高气体静压径向轴承的承载能力,势必需要增大入口压强。但这会改变气膜内部的流场结构,引起激波的出现,进而降低其承载力,而关于此问题,目前已有的文献对此涉及不多。针对进气口压强、偏心率及结构参数等对轴承气膜流场产生的影响展开系统研究,并分析其可能产生的激波并导致供气孔周围出现明显的压力降问题,以此提出针对节流孔结构改进的优化设计方案。
2 模型
目前,气体静压径向轴承的节流孔分布方式主要有两种:一种是双排供气,一种是单排供气。在同样的供气条件下双排孔轴承的承载性能和刚性更好,应用更广泛[7]。研究对象为双排孔供气轴承系统,如图1 所示。由于轴承内部气膜厚度h 远小于内径D,因此忽略气体在厚度方向的流动,仅考虑其在轴向以及周向的运动情况。

图1 静压气体轴承结构示意图Fig.1 Schematic Diagram of Aerostatic Bearing
节流孔处的气膜径向截面,如图2 所示。在气膜周向均匀排列五个节流孔,两排节流孔呈轴向对称分布,保证整个气膜流场的对称性和稳定性。基本参数,如表1 所示。
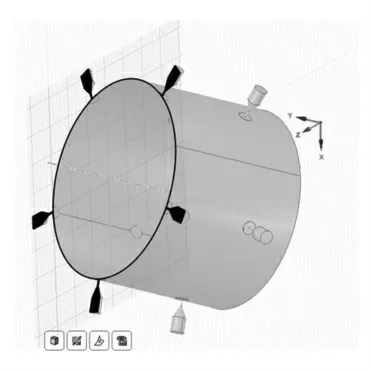
图2 气膜径向截面图Fig.2 Radial Section of Gas Film

表1 气体轴承基本尺寸以及运行参数Tab.1 Structure and Operating Parameters of Gas Bearing
3 CFD 仿真
3.1 控制方程及边界条件
根据气体润滑理论,任何流动问题都必须满足质量守恒方程。单位时间内微元体中质量的增加,等于同一时间间隔内流入该微元体的净质量,得到连续方程[8]:
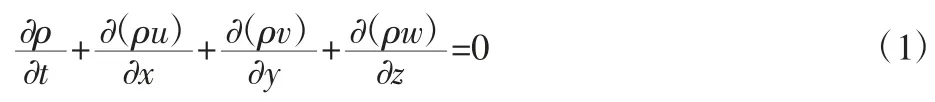
式中:ρ—密度;t—时间;u、v、w—速度在 x、y、z 方向的分量。
根据微元体中流体的动量对时间的变化率等于作用在微元体上的各个外力之和,得到N-S 方程[8]。

式中:p—微元体上的压力;μ—动力粘度;Su,Sv,Sw—动量守恒方程的广义源项,Su=Fx+sx,Sv=Fy+sy,Sw=Fz+sz,Fx,Fy,Fz是微元体上的体力,sx,sy,sz的表达式为:
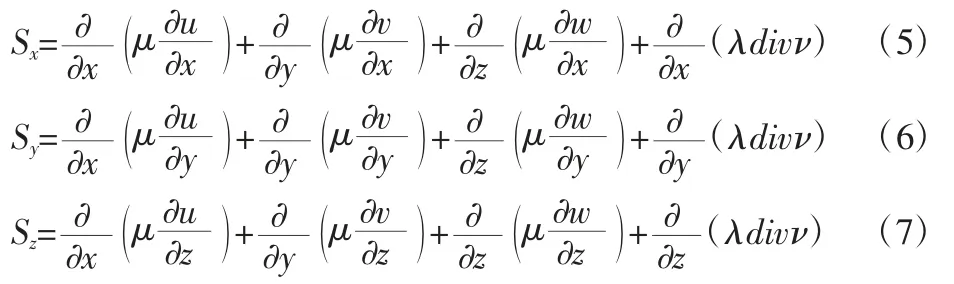
根据能量守恒方程[8,9]:
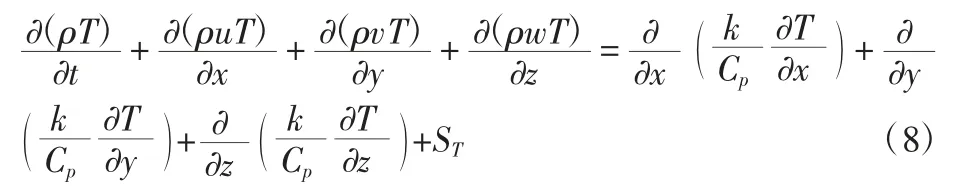
轴承两端边界条件为:

气体静压径向轴承出口的边界条件为:

式中:P0—轴承的出口压力,定义流体为理想气体。设置压力出口边界条件pout=pa。其中,Pa为标准大气压。
3.2 网格划分
建立气体轴承模型,在Gambit 中划分网格,如图3(a)所示。为保证计算的精度,对每个节流孔附近的网格做加密处理,如图3(b)所示。

图3 气膜网格划分Fig.3 Mesh of Gas Film
导入Fluent 软件,采用k-ξ 二方程模型基于压力的计算方法,并基于二阶迎风离散方法,设置收敛精度为10-4量级。气体粘度计算采用公式:

式中:μ0—标准气体粘度,μ0=1.716×10-5kg/(m·s);T—轴承内部气体温度;T0—大气温度,T0=273.11K;C—有效温度,C=110.56K。
4 结果与分析
当偏心率为0.4 时,轴承气膜压力云图,如图4 所示。
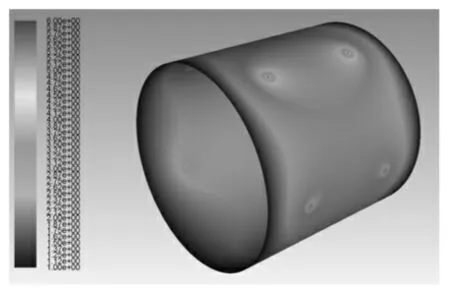
图4 气膜压力分布云图Fig.4 Cloud Chart of Pressure Distribution
由于转轴受负载后存在偏心,使得气膜被转轴和轴瓦压缩,气膜厚度变小,在节流孔附近压力突然减小,气体流速急剧真大,产生激波并出现涡流现象,使轴承承载力发生变化,节流孔处气体速度矢量图,如图5 所示。

图5 节流孔处气流速度矢量图Fig.5 Velocity Vector Diagram of Flow Field Near the Orifice
为系统研究偏心率对轴承内气体流场的影响,取供气压力为6 个大气压计算出不同偏心率下节流孔附近的气体密度等值线,如图6 所示。

图6 节流孔处密度等值线Fig.6 Density Contour Near the Orifice
从图6 可以看出,当偏心率较小时,轴承内流场密度分布较为平滑,如图6(a)所示。随着偏心率增大,局部气膜密度发生变化,如图6(b)所示。密度分布较大的区域更加聚集,而密度较小的区域更加稀疏,致使两个区域之间的压力差增大,承载力也随之增大,如图6(c)所示。在远离节流孔一端更容易出现紊流状态。偏心率影响下的承载力特性曲线,如图7 所示。

图7 承载力随偏心率变化曲线Fig.7 Bearing Capacity Curve with Eccentricity
由图7 曲线变化趋势还可以看出,随着偏心率的进一步增大,轴承承载力的增幅逐渐变缓。
为了研究涡流在不同供气压强条件的变化情况,逐渐增加供气压强,并提取不同供气压强下轴承节流孔附近的密度等值线,如图8 所示。
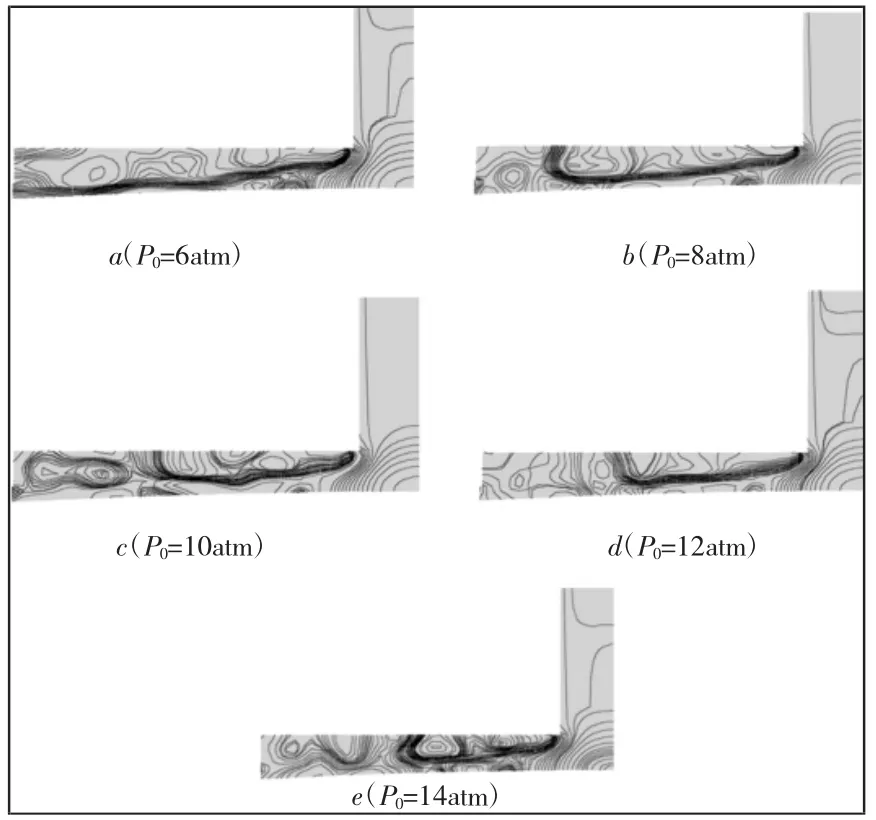
图8 节流孔处密度等值线Fig.8 Density Contour Near the Orifice

图9 节流孔处马赫数等值线Fig.9 Maher Number Contour Near the Orifice
当供气压力P0=6atm 时,在节流孔末端凸台附近产生单涡流,如图8(a)所示。随着供气压力的增大,气流受到轴承与节流孔壁的挤压,在流场附近产生的入射斜激波变得更加明显,出现双涡流,如图8(b)、图8(c)、图8(d)所示。随着供气压力的继续增大,双涡流逐渐分开,且逐渐向节流孔靠近,如图8(e)所示。不同供气压强条件下,节流孔附近气体马赫数等值线,如图9 所示。
当供气压力较低时,在远离节流孔一端的气体处于层流状态,如图9(a)所示。节流孔附的气体压缩量比较大,小孔与气膜连接处的环形区域内存在明显的回流现象,且最大马赫数出现在节流孔附近,离节流孔越远气体马赫数逐渐降低,随着供气压力的不断增大,气体流速不断增加,气体惯性力也不断增大,节流孔附近的气体最大马赫值也随之增大,如图9(b)、图9(c)、图9(d)所示。最大马赫数达到2.3,如图9(e)所示。激波及紊流现象更加明显,并能在一定程度上降低轴承的承载力。
气体轴承承载力变化情况,如图10 所示。
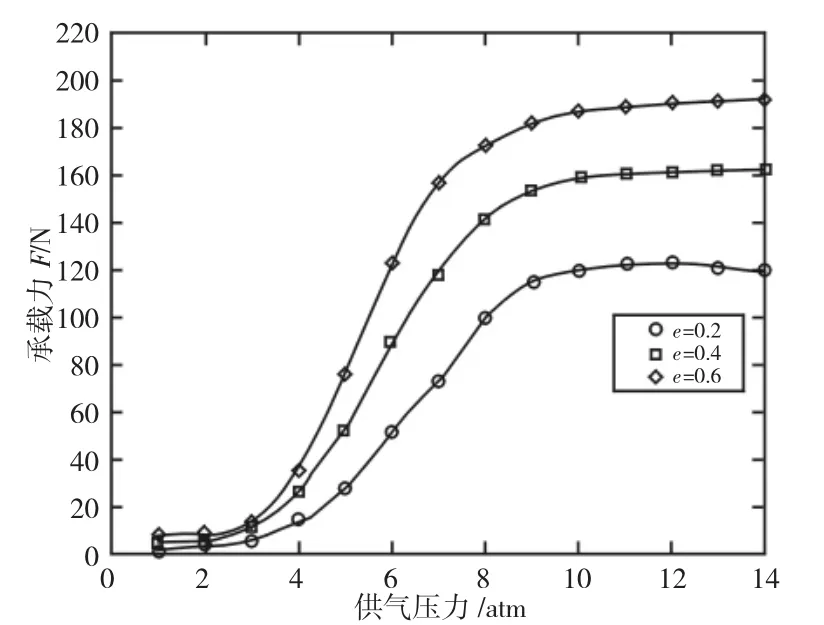
图10 不同供气压力下的承载力对比图Fig.10 Comparison of Bearing Capacity Under Different Gas Supply Pressures
由图10 可以看出,当供气压力小于3 个大气压时,由于供气压力较小,转子与轴颈间难以形成稳定的气膜,导致轴承承载力增幅缓慢;随着供气压力的增大,气体轴承的承载力逐渐增大;当供气压力大于8 个大气压后,供气孔转角处产生超音速气流,使气膜压力急剧下降,节流孔附近产生激波并形成涡流;当供气压力继续增大,节流孔附近气体流速也随之增大,压力降更加明显,且激波区域逐渐向节流孔附近收缩,在激波与边界层气体的相互作用下,产生局部紊流现象,随着供气压力的进一步增大,承载力增长变缓甚至开始呈下降趋势。
5 结构优化
从气体静压轴承的结构特性可以看出,当空气从节流孔入口进入轴承气膜中时,流场横截面积发生了突变,且气流的运动轨迹发生了90°的转弯,将导致较大的能量损耗。从前面的计算结果也可以看出[10],当增大入口压强时,节流孔附近气膜很容易出现激波及涡流现象,并导致轴承承载力的下降。以轴承的承载力为优化目标,以初始设定的壁面边界及出口压强为固定约束条件,将节流孔开口角度作为尺寸优化的设计变量,系统研究在不同入口供气压强条件下,节流孔的开口角度对气体静压轴承内部气膜流场及承载特性的影响。在满足所设定边界约束的条件下,寻找最优节流孔开口角度,使得轴承的承载力达到最大。
5.1 优化模型
改变节流孔的开口角度α,对比未优化前的模型,如图11 所示。
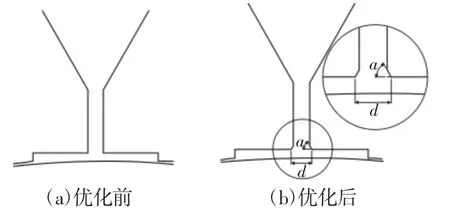
图11 节流孔优化前后截面图Fig.11 Section Diagram Before and After Orifice Optimization
5.2 优化结果
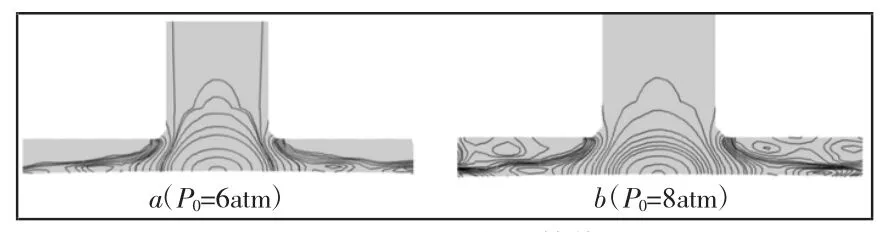
图12 节流孔处密度等值线Fig.12 Density Contour Near the Orifice

图13 节流孔处马赫数等值线Fig.13 Maher Number Contour Near the Orifice

图14 节流孔周向压力分布图Fig.14 Circumferential Pressure Distribution of Orifice
优化后节流孔附近的气体密度和马赫数分布情况,如图12、图13 所示。
图12(a)、图12(b)分别为供气压力为 6atm 和 8atm 时优化模型节流孔附近的气体密度分布图。对比优化前的气体密度分布图8(a)、图8(b)可以发现,在改变节流孔末端张角后,节流孔周围的气体压力有所提升且节流孔附近的涡流现象逐渐消失,气体密度分布更加均匀。且由图13 可以看出,优化之后节流孔周围由于局部气体压缩量降低,使最大马赫数有所降低(对比图9)。提取出节流孔圆周方向的气膜压力分布,如图14 所示。
对比优化前后节流孔附近压力分布可以看出,在节流孔附近存在明显的压力降。模型优化之后,供气孔末端张角增大,气体通过节流孔拐角的能量损失降低,使局部气体流速相对优化之前有所增大,导致节流孔周围的压力降幅度有所增加,但由于优化之后节流孔附近的涡流现象逐渐消失,使气膜的最大压力也有明显增大,节流孔圆周方向的压力也存在一定比例的增大。进一步增大供气压力,节流孔张角的改变对周围的压力影响则更加明显,但对气膜整体压力的增加幅度有所下降。
保持节流孔末端的孔径d 不变,改变节流孔张角α 大小,计算出不同供气压力下气体轴承的承载力变化情况,如图15 所示。
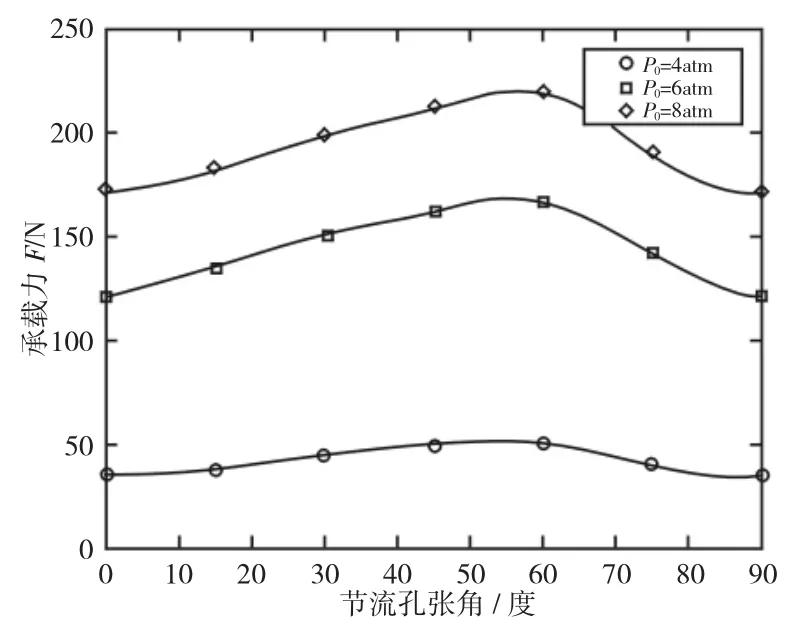
图15 不同节流孔张角的承载力对比图Fig.15 Comparison of Bearing Capacity with Different Orifice Angles
由图15 可看出,对比优化前的模型(即α=0°),随着节流孔张角的增大,供气孔与气膜之间的局部气体压缩量降低,节流孔附近涡流变小,从而增大轴承承载力。若节流孔张角继续增加时,供气孔周围的气体密度迅速降低,单位气体惯性力分量降低,并导致轴承承载力下降。根据建立的不同张角气膜承载力的拟合曲线,得到具体的优化前后数据对比,如表2 所示。

表2 优化前后数据对比Tab.2 Comparison of Data Before and After Optimization
由此可以得到,随着供气压力的增大,最优节流孔张角对轴承承载力的增幅也随之增大,节流孔最优张角介于(50~60)°之间。
6 结语
利用Fluent 软件对气体静压径向轴承在不同参数条件下的气膜流场进行仿真研究,分析偏心率、供气压力及节流孔结构参数对气膜流场及承载特性的影响,得到以下结论:
(1)随着轴承的偏心率逐渐增大,局部气膜密度发生变化,密度分布较大的区域更加聚集,致使轴承上下区域之间的压力差增大,承载力也随之增大。偏心率有助于提高轴承的承载力。但当偏心率过高时,轴承受供气压力的影响随之增大,使轴承的稳定性降低。
(2)承载力随供气压力的增大而增大,当供气压力P0<3atm时承载力增幅缓慢,当供气压力3atm
(3)改变节流孔张角,可实现气体静压轴承结构的优化,使得节流孔附近的涡流现象逐渐减小,节流孔周围的气体压力有所提升,气体密度分布更加均匀。气体通过节流孔拐角的能量损失降低,进而提高轴承承载力。且供气压力越大,最优节流孔张角对轴承承载力的增量越大,最优节流孔张角介于(50~60)°之间。
