基于改进鲸鱼算法光伏阵列MPPT 的研究

孙荣霞，尚娅慧，韩 帅

(河北大学 电子信息工程学院，河北 保定071002)

0 引言

随着化石能源的消耗以及环境污染的日益加重，绿色可再生能源的开发越来越深入人心，太阳能作为一种无污染、低成本、储量大、无噪音的新型能源越来越受到人们的青睐[1]。 光伏电池是利用太阳能的主要装置，但光照强度和温度对光伏电池的输出特性有直接影响，外界因素改变时，光伏电池的最大功率点也会发生改变。 为了使光伏阵列一直输出最大功率值，有必要对光伏阵列的最大功率点进行跟踪。

目前有多种传统算法已经实现了对最大功率点的追踪，如扰动观察法(Perturbation & Observation，P&O)、电导增量法(Incremental Conductance，InC)、模糊控制法(Fuzzy Control，FC)、恒定电压法(Constant Voltage Tracking，CVT)等，但当遇到阴影遮挡存在多峰现象时，此类方法追踪效果失效。 针对此现象提出了很多智能算法，如粒子群算法(Particle Swarm Optimization，PSO)[2]、蚁群算法(Ant Colony Optimization，ACO)[3]、改进蝙蝠算法(Bat Algorithm，BA)[4]、灰狼算法(Gray Wolf Optimization，GWO)[5]等都已经应用到多峰寻优中， 但是这些算法稳定性普遍不高，易陷入局部最优解。

MIRJALILI S[6]等人在2016 年提出了一种新型智能算法——鲸鱼优化算法(WOA)，并与粒子群算法、引力搜索算法(Gravitational Search Algorithm，GSA)等进行测试比较， 结果显示WOA 算法的参数少、 操作简单、收敛性更好。2017 年HASANIEN H M[7]利用鲸鱼算法实现了最大功率点跟踪， 改善了光伏系统动态电压响应。 但鲸鱼算法搜索速度慢，对MPPT 进行追踪功率输出不平稳，损失部分能量，为克服上述问题，本文将改进的鲸鱼算法应用到最大功率点追踪上。

1 基本鲸鱼算法

鲸鱼算法模拟了座头鲸一种特殊的狩猎机制——泡泡网觅食方法[8]，这种捕食机理可简单表述为：鲸鱼潜入水深10 ～15 m 处围绕猎物，在猎物周围以螺旋的姿势逐渐收缩范围向水面游动，游动的同时吐出大小不等的气泡，所吐气泡形成环形或者方形的气泡网紧紧包围猎物，进而对猎物进行攻击捕食。 最优猎物相当于光伏阵列的最大功率点，鲸鱼环绕搜索找寻猎物的过程相当于对光伏阵列最大功率点进行寻优的过程。

下面对鲸鱼捕食的三个阶段进行数学建模：(1)随机搜索猎物；(2)环绕猎物；(3)对猎物进行气泡攻击捕食。

1.1 猎物搜索(全局搜索)

在初始位置鲸鱼搜索觅食时对猎物进行随机搜索，对应着鲸鱼算法的全局搜索阶段，此时数学模型中的系数向量|A|＞1，此阶段的计算公式如下：

其中，X(t)表示当前鲸鱼个体的位置，Xrand表示目前鲸鱼群体中随机一只鲸鱼所处的位置，A 和C 表示系数向量，系数向量的计算公式如下：

其中，a 在迭代过程中由2 线性递减为0；r 为[0，1]的随机向量；t 表示当前迭代次数，Tmax代表最大迭代次数。

1.2 环绕猎物

环绕猎物阶段中，每只鲸鱼代表算法中独立的一个个体，每个个体在搜索空间中的位置代表寻优过程的一个解，最佳捕食位置在搜索空间中是未知的，WOA 算法最优候选解为最优鲸鱼所处位置 (猎物)， 确立最优解后其他搜索个体逐步向最优鲸鱼搜索个体(猎物)逼近。 根据鲸鱼环绕猎物的方式由以下数学式表示：

式中t 表示当前迭代次数，X(t)表示当前鲸鱼的位置，X*(t)表示最优鲸鱼所处的位置，X(t+1)表示目标猎物所处的位置。

1.3 气泡攻击捕食(局部搜索)

气泡捕食法模拟的是鲸鱼的局部寻优过程，此时数学模型中的系数向量|A|＜1，对鲸鱼气泡捕食进行数学建模，设计了两种更新位置的策略，分别如下：

(1)收缩包围机制

鲸鱼位置的更新由式(7)来表示，当|A|＜1 时，搜索者的下一个位置可能存在于当前位置和猎物之间的任何一个位置。

(2)螺旋捕食机制

鲸鱼通过螺旋形运动式搜索，位置更新的公式如下：

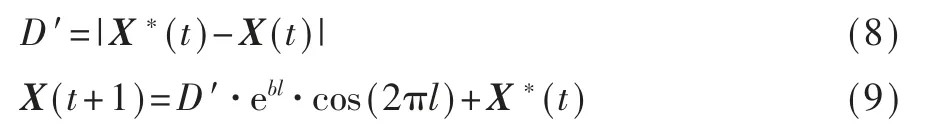
其中，D′是目前鲸鱼个体与最优鲸鱼个体的距离，b 为常量系数，l 为[-1，1]之间的随机量。

气泡攻击捕食时两种机制同时进行，概率均为0.5，计算公式如下：

其中，p 为[0，1]之间的随机数。

2 改进的鲸鱼算法

鲸鱼算法与其他智能算法相比有很多优点，但基本的鲸鱼算法在处理高维度复杂问题时存在收敛速度慢、局部最优解等问题，所以在算法优化领域中提出了一些改进后的鲸鱼算法，本文是将一种改进的鲸鱼算法应用到解决最大功率点跟踪的问题。

鲸鱼算法中的收敛因子a 在迭代过程中呈线性收敛的趋势， 不符合鲸鱼实际迭代寻优搜索过程[9]，该控制算法在处理高维度复杂问题时需要避免早熟问题的出现，因此，本文为平衡全局搜索和局部搜索能力，应用余弦形式的递减方式，具体表达式如下：

其中，t 是当前迭代次数，Tmax是最大迭代次数，改进前后的a 值如图1 所示。

图1 改进前后a 的对比图

参数a 值的改变决定系数向量A 的变化，进而协调算法的全局搜索和局部搜索，由图1 可知，改进后的a 值初期较大且递减程度缓慢，可以更好地进行全局寻优； 迭代后期，a 值的递减速度加快，以便进行局部寻优。 文献[10]提出在算法中引入多项式变异可以进一步提高算法跳出局部最优的能力，同时文中已经用15 个测试函数对算法的寻优进行测试，得出参数的余弦改进策略优于线性改进策略，可以有效平衡全局搜索和局部搜索能力。

惯性权重值大时全局搜索能力强，惯性权重值小时局部搜索能力强[11]。 所以本文借鉴前面收敛因子a 的余弦变化应用一种新的非线性惯性权重，随着迭代次数增加动态调节全局搜索和局部搜索能力的同时加快算法收敛速度，提高寻优精度。

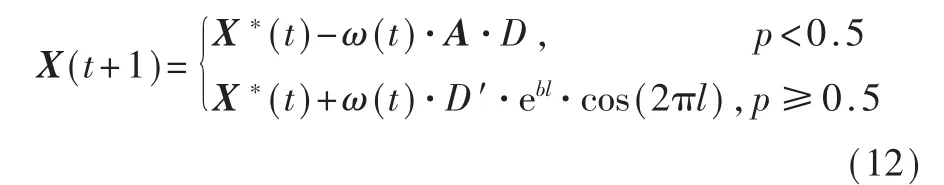
权值ω(t)的表达式为：

迭代次数初期t 值较小，权重ω 较大,算法的调整步长也大，鲸鱼可以在大范围空间中搜寻最优解。随着迭代次数t 的增加，权重ω 反而越来越小，算法调整步长也变小，此时的鲸鱼在最优解邻域空间中进行精细搜索。 ω 随着当前鲸鱼群迭代次数的改变自适应变化，提高了鲸鱼算法的收敛精度，加快了收敛速度。

3 改进鲸鱼算法的最大功率点跟踪

(1)鲸鱼参数初始化

初始化鲸鱼的种群个数n，系数向量A、C，收敛因子a，最大迭代次数Tmax以及鲸鱼移动的位置向量等。

(2)目标函数

根据适应度函数计算所有鲸鱼的适应度值，把适应度值高的鲸鱼位置保留下来，适应度值低的鲸鱼朝着猎物方向搜索，目标函数即适应度函数，本文的目标函数为光伏阵列的功率。

(3)更新方法

通过搜索、包围、攻击猎物对鲸鱼的位置信息进行更新，使鲸鱼向最大功率点方向靠近捕食。

(4)终止阶段

反复进行迭代会造成功率的不稳定，进而造成阵列的输出效率降低，所以要快速将输出功率稳定在最大功率点处，进一步提高整个系统的输出效率。鲸鱼算法的终止条件为：鲸鱼位置标准差小于某个特定的阈值或者迭代次数t 达到最大值时，将最优鲸鱼的位置作为最终优化计算结果，输出鲸鱼位置对应的占空比控制信号，控制光伏阵列工作，使其稳定在最大功率点。

(5)算法重启

输出功率随外界环境改变时追踪到的最大功率点的数值会发生变动，此时需要重启改进鲸鱼算法，重新启动系统，寻找新的最大功率点，重启条件为：

其中，PN表示实时采样功率，PM表示最大功率，ΔP表示功率的变化值，ΔPth表示预先设置好的阈值。

4 仿真结果分析

如图2 所示，本文选用3 块光伏电池串联，利用MATLAB/Simulink 建立仿真模型，采用鲸鱼算法(WOA)、改进鲸鱼算法(IWOA)、电导增量法(INC)在不同环境下对光伏阵列MPPT 进行追踪。 光伏电池的参数设置为：Voc=43.6 V，Isc=8.35 A，Imp=7.60 A，Vmp=35.0 V，求解器为ode45，仿真时间为0.3 s；Boost 电路的参数 为L=10 mH，C1=50 μF，C2=100 μF，R=50 Ω，f=50 kHz。 采用不透光的塑料薄膜进行遮挡形成阴影环境。

(1)实验一：3 个光伏电池均匀光照，光照强度以及温度如下：

图2 最大功率跟踪电路示意图

模块1：Sun=1 000 W/m2，T=25 ℃

模块2：Sun=1 000 W/m2，T=25 ℃

模块3：Sun=1 000 W/m2，T=25 ℃

三个串联模块的P-V 特性曲线如图3 所示，鲸鱼算法和改进鲸鱼算法仿真对比图如图4、图5所示。

图3 均匀光照下光伏阵列的P-V 特性曲线

当光伏阵列处于均匀光照时，如图3 所示，光伏阵列的P-V 曲线为单峰型， 最大功率点处的值为797.6 W。 图4 中鲸鱼算法的仿真曲线在0.078 s 时追踪到最大功率，其值约为795.6 W(串联时总功率为797.6 W)，但前期振荡较大，误差值为2 W，追踪到的精度为99.75%； 而改进的鲸鱼算法追踪到的最大功率点为797.4 W，功率输出较平稳，误差值为0.2 W，搜索到最大功率点的时间为0.057 s，追踪到的精度为99.97%，由此可知采用改进鲸鱼算法进行MPPT 控制时搜索时间短，误差值小，精度高。

(2)实验二：遮挡一块光伏阵列，光照强度及温度参数如下：

图4 均匀光照下鲸鱼算法仿真特性曲线

图5 均匀光照下改进鲸鱼算法仿真特性曲线

模块1：Sun=1 000 W/m2，T=25 ℃

模块2：Sun=1 000 W/m2，T=25 ℃

模块3：Sun=800 W/m2，T=25 ℃

三个串联模块的P-V 特性曲线如图6 所示，局部遮阴时鲸鱼算法(WOA)、改进鲸鱼算法(IWOA)、电导增量法(INC)的仿真结果如图7、图8、图9 所示。

图6 局部遮阴下光伏阵列的P-V 曲线

图7 局部遮阴下鲸鱼算法仿真特性曲线

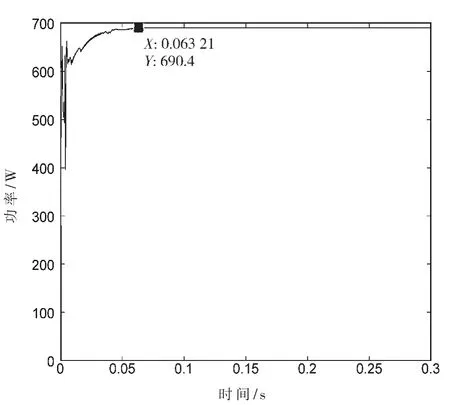
图8 局部遮阴下改进鲸鱼算法仿真特性曲线

图9 局部遮阴下电导增量法的输出特性曲线

在遮挡一块光伏电池时，P-V 曲线呈现双峰型，如图6 所示，光伏电池的总功率为690.5 W，局部极值点处的值为525.6 W。 图7 中在0.09 s 时鲸鱼算法追踪到的最大功率值为686.9 W，误差值为3.6 W，精确度为99.48%；图8 中改进鲸鱼算法在0.063 s时追踪到最大功率值为690.4 W，与实际值相差0.1 W，跟踪到的精度值为99.98%；图9 中的电导增量法追踪到局部极值点为525.4 W，能量损失严重，跟踪失效。 由此可知改进鲸鱼算法的误差值相对较小，跟踪精度高，搜索时间短，所以改进鲸鱼算法寻优性能更好。

5 可变状态下的阴影仿真

光伏系统运行过程中会受到光照强度和温度的影响，因此动态阴影环境的改变也是光伏MPPT研究的重点，光照强度改变的光伏阵列P-V 曲线如图10 所示，局部阴影1 中3 块光伏电池光照强度分别 为S1=1 000 W/m2，S2=1 000 W/m2，S3=800 W/m2。在0.15 s 时光照强度突变；局部阴影2 的光照强度为S1=1 000 W/m2，S2=800 W/m2，S3=600 W/m2。

由图10 和图11 可知光伏阵列在局部阴影1时理论上输出的最大值为690.5 W，在0.063 s 时改进鲸鱼算法追踪值为690.4 W，跟踪精度为99.98%，0.15 s 时光照强度发生改变，对最大功率点进行再次追踪。 在0.197 6 s 时系统功率达到理论上的最大值为518.6 W，系统状态2 的实际值为517.3 W，跟踪精度为99.75%。 通过以上分析得知，在光照强度发生改变时本文改进的鲸鱼算法依然能实现对最大功率点的跟踪。

图10 可变阴影下光伏阵列的P-V 特性曲线

图11 可变阴影下改进鲸鱼算法仿真特性曲线

6 结论

针对光伏系统局部阴影条件下P-V 特性曲线呈现多峰的状态，本文提出应用改进的鲸鱼算法对光伏阵列最大功率点进行追踪，通过本文仿真分析得出，改进的鲸鱼算法中将收敛因子由线性递减形式改为余弦递减形式，并且加入与余弦控制参数a 同步变化的非线性惯性权值，有效平衡全局搜索和局部搜索能力，收敛速度加快，收敛精度提高。同时改进的鲸鱼算法也适用于光照发生改变的状况，在局部阴影发生改变时依然能快速准确地追踪到最大功率点。