输气管道泄漏模型不确定性因素敏感性分析
2021-01-27安建川
安建川
中国石油西南油气田分公司输气管理处,四川 成都610213
引言
长输油气管道发生意外泄漏后,可能引发火灾、爆炸等次生灾害,造成严重后果,科学准确地评估管道失效后果,对于重新认识事故以及应急救援工作的开展具有重要的现实意义。然而,无论是管道的泄漏程度还是火灾、爆炸造成的失效后果都存在着极大的不确定性;充分考虑因素的不确定性,才能为管理、决策提供可靠依据。风险评价的不确定性来源于模型和场景参数等因素取值的不确定性;对于选定的模型,场景参数的选取成为引起评价不确定的主要因素,为此,油气管道泄漏模型不确定性因素分析成为当前研究热点。
熊鸿斌等认为[1-2],影响天然气泄漏的主要不确定因素为泄漏孔径、风速和环境温度,并给出了3 个不确定性因素的数据来源及其概率分布函数。HSE 和Beerens 等均指出[3-4],泄漏速率的取值大小直接影响着风险评价结果,并给出了泄漏速率的取值范围。刘中良等研究了天然气管道临界泄漏和亚临界泄漏过程[5],分析了泄漏孔径、管径和初始压力对泄漏速率的影响,指出泄漏孔径对泄漏速率的影响最大。韩光洁[6]分析了埋地天然气管道泄漏扩散规律,指出泄漏孔径、风速、环境温度和埋地深度是影响甲烷浓度分布的重要因素。杨凯指出[7],城市燃气管道泄漏灾害发生的不确定性因素包括大气稳定性、大气压、温湿度、风速等气象因素,地表植被、城市建筑物密集度等地形地貌因素。Henry 认为[8],泄漏孔形状和面积、泄漏地理状况和环境因素等具有随机性,因素的随机性使得数学模型的计算结果具有较大的不确定性。沈斐敏认为[9],燃气泄漏风险中主要的不确定性因素为泄漏孔面积、流量系数、燃气压力和环境温度,并讨论了各因素的取值范围。可见,影响管道泄漏速率的不确定性因素众多,而各因素对泄漏速率影响程度不同,若将所有因素都作为不确定性因素纳入泄漏速率计算,不仅导致计算量巨大,而且无法获知各因素对泄漏速率的影响主次,为此,需要分析泄漏速率对各因素的敏感度,从而减小计算量,实现准确、迅速评估泄漏风险。
传统分析参数敏感度的方法为单因素分析法[10-12],其基本思想为:当分析某一因素对目标函数的影响时,保持其余因素取值不变,仅使该因素在其给定的范围内变化。若该因素的变化能引起目标函数发生较大变化,则说明目标函数对该因素很敏感,即该因素的敏感度大;若该因素的变化仅能引起目标函数发生较小变化,则说明目标函数对该因素不敏感,即该因素的敏感度小。
然而,在输气管道泄漏模型中,由于影响因素较多且相互关联,各因素变化会共同影响模型对泄漏率的计算精度,因此,有必要在调研确定影响输气管道泄漏风险的主要不确定性因素基础上,开展泄漏模型多因素敏感度整体分析。即:当所有因素取值在各自指定的范围内同时变化,分析各因素变化对目标函数变化程度的贡献率。
1 输气管道泄漏模型及主要影响因素
1.1 输气管道泄漏模型
天然气受压从管道裂口处泄漏时,采用气体绝热流动方程计算其泄漏速率[13-14]。由于泄漏孔径大小不同,泄漏速率计算模型又分为小孔模型、管道模型和大孔模型。

1.1.1 小孔模型
假设泄漏孔为圆形,当泄漏孔径与管径比不大于20%时,采用小孔模型计算泄漏速率。
根据天然气在管道内的流动状态不同,又分为亚音速流动和音速流动下的泄漏速率计算公式。天然气亚音速流动时

由于小孔泄漏对管道内天然气流动影响较小,故取p2=p1,T2=T1,即认为天然气泄漏速率不随时间变化,恒等于起始泄漏速率。
1.1.2 管道模型
当泄漏孔径与管径比不小于50%时,采用管道模型计算泄漏速率。此时,取p2=pa,泄漏速率用式(1)和式(4)联立计算
1.1.3 大孔模型[15]
当泄漏孔径与管径比在20%∼50%时,采用大孔模型计算泄漏速率。
大孔模型假设所有流入管道的气体全部经孔口泄漏,因此,根据连续性方程,可得
式中:
AD管道横截面积,m2;
Ma1管道起点马赫数,无因次;
Ma2泄漏孔处的马赫数,无因次。
管道起点与泄漏孔处的参数关系为

当管道内天然气为亚音速流动、泄漏孔处天然气为音速流动时,泄漏速率为
当管道内及泄漏孔处天然气均为亚音速流动时,泄漏速率为
1.2 输气管道泄漏主要影响因素
影响管道泄漏速率的因素包括储存物质的物理化学性质、泄漏源的几何形状、生产运输条件、气象、地形地势和地面性质共6 类。其中,物质的物理化学性质取决于所管输介质,泄漏源的几何形状主要指泄漏孔形状、孔径大小等,生产运输条件主要指压力、流量等,气象包括风速、风向等,地形地势和地面性质两类因素主要包括地貌、有无建/构筑物等[16-20]。对于输气管道泄漏,结合泄漏模型可知,由于管输介质是确定的,管道通常埋地敷设,泄漏模型假设泄漏孔为圆形且模型中泄漏速率与压力、温度以及泄漏点距起点的距离紧密相关,因此,输气管道泄漏速率计算的主要不确定性因素取为起点压力、泄漏孔面积(泄漏孔径)、气体温度和泄漏点距起点距离。
2 多因素敏感性整体分析方法
2.1 多因素敏感性整体分析方法建立
多因素敏感性整体分析方法建立的关键有两点,一是确定因素在其各自范围内的抽样取值方法;二是建立非线性参数统计方法分析目标函数对各因素变化的敏感程度[10-12]。
2.1.1 拉丁超立方抽样法
为了确保每个因素的随机抽样样本能在指定的取值空间内均匀分布,且不重复抽样,采用拉丁超立方抽样法取样[21]。以m个不确定性因素组成的因素集{x1,x2,···,xm},共抽样n次为例,说明该方法的实现步骤。
(1)将每个因素xi的取值空间按照等概率密度的方式划分为n个彼此相邻的取值区间
(2)在xi的n个区间内分别随机抽取一个样本(κ=1,2,···,n),共抽取n个样本组成xi的样本集
(3)随机排列xi的n个样本,可生成n个排列。
(4)对于因素集{x1,x2,···,xm},每次选定n个排列中的一列(如第κ 列,κ=1,2,···,n,下同)构成因素集的一个样本集,记为Xκ;抽样n次,即可得到n个样本集{X1,X2,···,Xn},形成一个n×m的因素样本集矩阵,完成因素集的样本抽样。
2.1.2 Spearman 秩相关系数分析法
为了分析具有非线性关系的多个因素对泄漏模型的影响,采用Spearman 秩相关系数分析法[22-24]。Spearman 秩相关系数分析法是一种非线性参数统计分析方法,通过对比每个样本集中某因素取值对应的次序变化引起目标函数值的次序变化来分析变量随机值之间的相关性,从而确定各因素对模型的影响程度。该方法的优点是不受因素取值大小限制,只需考察因素样本集与目标函数值的排序位置变化,因而更适合多因素同时变化情况下,分析目标函数对各因素的敏感性。以前述m个不确定性因素组成的n个样本集{X1,X2,···,Xn}为例,说明该方法的实现步骤。
(1)将n个样本集{X1,X2,···,Xn} 分别代入泄漏模型,进行n次计算后,得到目标函数解集{Y1,Y2,···,Yn}。
(2)将每个因素xi的样本集按值的大小排序,序列中所处位置即为的秩,即为ακ。
(3)将目标函数解集{Y1,Y2,···,Yn} 按其因素对应值的大小排序,序列中Yj所处位置即为Yj的秩,即为βκ。
(4)按式(11)计算因素样本集与对应的目标函数解集的秩相关系数ri,该系数ri以绝对值表示,其值代表了目标函数对因素xi的敏感度;ri值越大,说明目标函数对因素xi的敏感度,即,因素xi对目标函数的影响越大,反之,亦然。

式中:rixi的秩相关系数,无因次;
n—区间数;
κ—样本集个数;
ακ-的秩;
βκ目标函数解集Yj的秩。
2.1.3 单因素分析法
因素敏感性分析的传统方法是单因素分析法[25-26],该方法的原理是:固定其他因素,逐一分析每个因素单独变化所引起的目标函数变化大小,由此判定目标函数对各因素的敏感度。这种方法能确定单一因素对目标函数的影响程度,适用于各因素之间相关性较小的线性模型。但当所分析的模型高度非线性时,由于单因素分析法忽略了因素之间的相关性,未考虑因素相互作用对目标函数的影响,因而对因素敏感性的识别度较低。
2.2 多因素敏感性整体分析方法应用实例
2.2.1 工程实例
某实际输气管道全长311.94 km,设计输量1 200×104m3/d,于2008 年投产。管道基本参数为:材质L485,外径813.0 mm,管壁厚度8.8 mm,设计最高压力10 MPa,运行压力4.7∼5.8 MPa。
研究管段起于A 站、止于B 站,管段长度20.36 km,距A 站10.60 km 处有一段长约500 m的高后果区管段,见图1。

图1 研究管段上下游阀室关系Fig.1 The relationship between upstream and downstream valve chambers of studied pipe
2.2.2 输气管道泄漏模型多因素敏感性整体分析
泄漏模型中有起点压力、泄漏孔径、气体温度和泄漏点距起点距离共4 个不确定性因素,它们相互关联,共同影响管道泄漏速率,因此,需开展多因素敏感度整体分析,研究4 个因素在各自取值区间内同时变化时,泄漏速率受单个因素的影响程度。
4 个不确定性因素取值区间分别为:泄漏孔面积7.850×10−5∼4.966×10−1m2(由于输气管道既可能发生小孔泄漏、大孔泄漏,也可能发生管道泄漏,因此,假设泄漏孔为圆形,泄漏孔径在1.000×10−2∼7.951×10−1mm 变 化),起点压力4.7∼5.8 MPa,气体温度273∼291 K[27-28],泄漏点距起点距离10 900∼11 400 m,分析过程如下。
(1)分别在各因素的取值区间内进行拉丁超立方抽样,抽取500、1 000、2 000 和3 000 份样本,500和3 000 份样本分布图如图2∼图5 所示。
(2)得到不确定性因素在四维空间中随机、均匀分布的样本集后,计算Spearman 秩相关系数,如表1 所示。

图2 泄漏孔面积样本分布Fig.2 Distribution of leakage area samples

图3 泄漏点距起点距离样本分布Fig.3 Distribution of distance between leakage point and starting point samples

图4 气体温度样本分布Fig.4 Distribution of gas temperature samples
在4 因素的敏感度整体分析中,每个因素自身的秩相关系数不仅与本因素的取值有关,同时还依赖于其他因素的取值。
从表1 中可见:(1)不同样本数下计算得到的各因素Spearman 秩相关系数值不同,但各因素敏感度排序却基本一致:泄漏孔面积的敏感度值最大,其次是气体温度,起点压力和泄漏点距起点距离的敏感度值相对较小;即泄漏孔面积对泄漏速率的影响最大,其次是气体温度,起点压力和泄漏点距起点距离对泄漏速率的影响较小。(2)样本数量为500 时得到的不确定性因素Spearman 秩相关系数排序与样本数量为1 000,2 000 和3 000 时得到的不确定性因素Spearman 秩相关系数排序趋势相同,说明在现有因素取值区间内,抽样数量大于500 时的模型计算结果已具备可靠性,能够满足后续风险分析的精度要求。
图5 起点压力样本分布Fig.5 Distribution of starting pressure samples
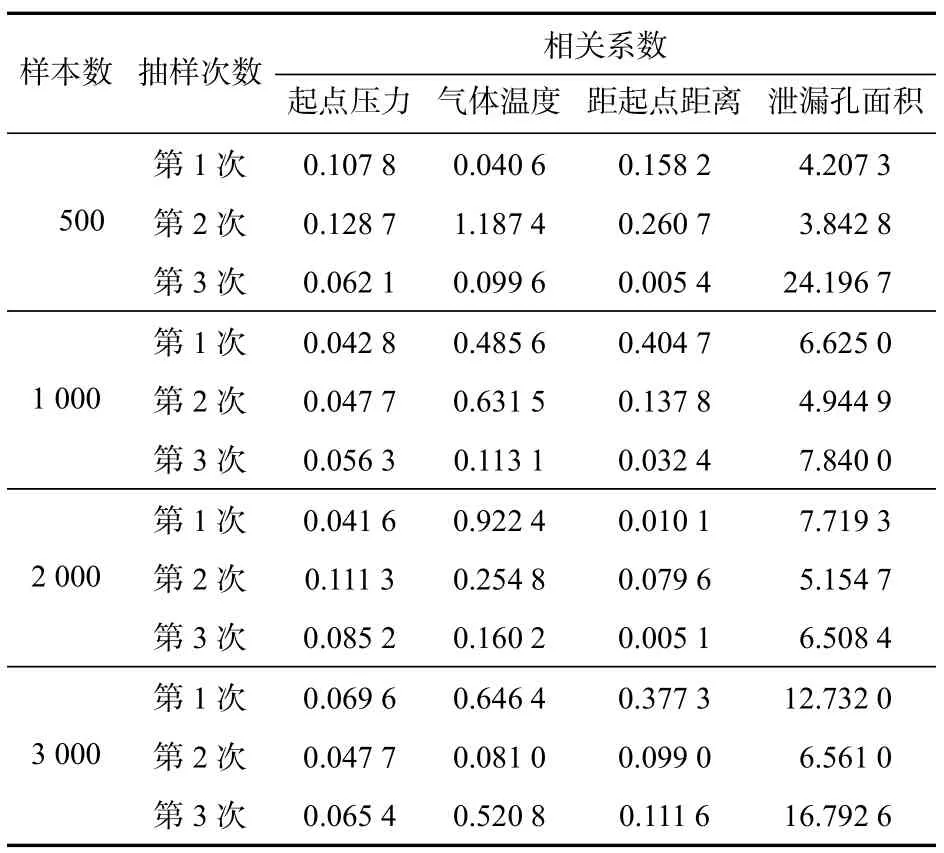
表1 各不确定性因素的Spearman 秩相关系数Tab.1 Spearman rank correlation coefficient of each uncertainty factor
3 结论
(1)调研国内外文献并结合输气管道泄漏模型可知,起点压力、泄漏孔面积(泄漏孔径)、气体温度和泄漏点距起点距离4 项为影响输气管道泄漏速率计算的主要不确定性因素。
(2)输气管道泄漏模型中多因素相互关联、共同影响:泄漏孔面积对泄漏速率的影响最大,其次是气体温度,最后是起点压力和泄漏点距起点距离;在现有因素取值区间内,抽样数量大于500 时的模型计算结果已具备可靠性,能够满足后续风险分析的精度要求。
